基于岭回归的坐站交替模式作业效率研究*
2021-08-23白圣亚林文文张岳君安元超
□ 白圣亚 □ 林文文,2 □ 张岳君 □ 安元超
1.宁波大学 机械工程与力学学院 浙江宁波 315211 2.宁波大学 先进储能技术与装备研究院 浙江宁波 315211 3.乐歌人体工学科技股份有限公司 浙江宁波 315191
1 研究背景
工作有关肌肉骨骼疾患多发于作业姿势单一且时间较长的职业,主要表现在腰部、肩部、颈椎等部位[1]。久坐会导致大脑昏沉、肩膀和背部酸痛等一系列问题,长此以往,会导致很多累积性疾病,如各类慢性病、脊柱疾病、心肺功能疾病等[2]。这一问题除工作自身因素外,还与不符合人体工程学的办公环境密切相关。长时间站立也会对工作和健康产生负面影响,Baker等[3]研究发现,站立工作2 h会引发肌肉疲劳、下肢水肿、认知功能下降等。在ISO 6385:2016《工作系统设计的人类工效学》中,提倡采用坐站交替的办公方式,避免久站或久坐不动所带来的潜在危害。日常办公环境中,每个人都有固定的工位,使用升降桌,可以在不改变工位的条件下实现作业姿势的转变,进而在不减少工作时长的情况下避免单一作业姿势的危害。
目前,国内有多家企业从事升降桌的设计与制造,但对升降桌使用功效的研究非常匮乏,与行业发展现状不匹配。当前,升降桌市场正处于快速发展机遇期,Credence Research公司市场调研报告认为,至2025年全球升降桌市场的规模将达到28亿美元,并以每年10%以上的幅度增长。国外对于坐站交替模式的研究较为丰富。Sui等[4]认为引入站姿作业的办公模式不会影响作业效率和表现,与之相对应的散步机和动感单车则可能对作业效率产生一定负面影响。Chambers等[5]发现升降桌有助于改变人们的行为模式,减少静坐时间和降低体感不舒适性的效果较为突出,同时不会影响工作绩效及相关健康指标。Karakolis等[6]认为升降桌可有效降低由久坐引起的下背部不适感,并且不会降低人们的工作效率。MacEwen等[7]指出使用升降桌对人体生理指标的影响较为轻微,且不影响作业效率,而散步机对生理指标的改进效果则较为显著。国内研究学者对坐站交替办公模式下的肌肉疲劳和舒适度做了一些研究。管培琪等[8]测试发现,久坐姿态下背阔肌的肌电信号中值频率和平均功率频率都有显著下降趋势,而坐站交替模式下背阔肌的肌电信号中值频率呈现温和下降,平均功率频率未检测到显著的下降变化,表明坐站交替对人体上半身肌肉的影响并不明显。王丽君[9]测试了四个桌面高度对作业舒适度的影响,马晓红[10]通过问卷调查和仿真方法确立了机械式升降桌的桌面高度范围,但是这两项研究在电动升降桌领域的适用性都比较弱,且对于使用升降桌对工作效率的影响未进行研究。综合来看,坐站交替工作模式可在不影响人们办公效率与身心健康的条件下减少久坐时间,缓解腰背部的不适与工作压力,是对现有单一坐姿办公模式的有效改进。
虽然国外科研人员对于坐站交替模式的工作效率做了一定的研究,但是工作任务一般设置为夹取、点击、熨烫等手工作业,与广大白领人群的工作任务不符,并且坐站时间的设定过长或过短,不符合日常办公的需求,缺乏符合日常办公条件的作业内容测试与分析。多数文献侧重于不同试验方案之间的比较,来证明坐站交替办公模式的优势,忽略了试验测试过程相关指标的变动与监测,未对影响受试者表现的潜在因素进行探究,这些因素对改进升降桌的使用方法至关重要。针对上述问题,笔者尝试设计一种试验来模拟日常办公,利用重复测量方差分析检测坐站阶段作业效率的变化水平。由于工作效率受个人因素影响较大,个体的工作效率大致会稳定在一个区间,因此为了避免传统线性回归所造成的过拟合,对数据进行标准化处理,同时在目标函数中加入正则项,进而转化为岭回归,具有更强的泛化能力来预测坐站交替模式下的工作效率[11]。
2 试验方法
招募20名不同年级的大学生作为受试者,其中男性10人,日均计算机使用时间为4.95±1.11 h;女性10人,日均计算机使用时间为3.97±2.36 h。受试者均身体健康,无腰腿部位肌肉劳损或其它部位不适。
整个试验过程分为两个部分,如图1所示。适应性测试包含10 min的坐站交替作业,目的在于获取受试者作业效率的基准水平,同时使其适应当前的测试环境。正式测试分为站30 min、坐45 min、站15 min三个阶段,每个阶段结束后记录对应的作业效率,作业期间每隔15 min提供短暂的姿势调整。在适应性测试和正式测试之间设置15 min的休息恢复时间,整个试验过程要求被测人员保持轻松站立,避免单脚受力,桌面根据受试者自身的需求合理调整。
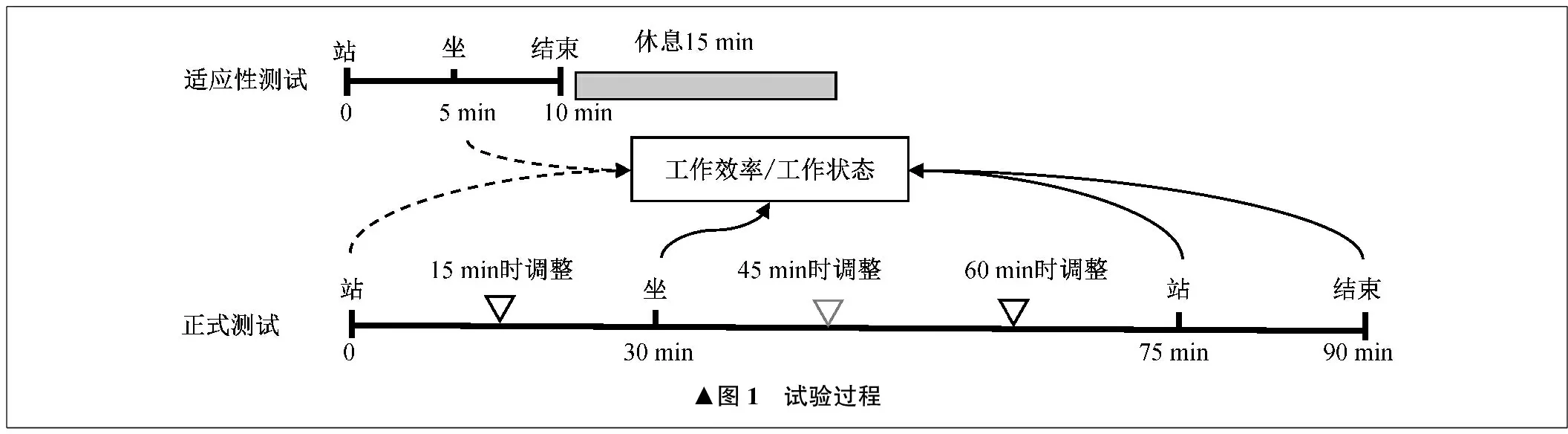
▲图1 试验过程
试验期间受试者根据随机选取的文章,采用拼音输入法在计算机软件中输入文章内容,工作效率的评价指标为打字效率,即每分钟的打字数量。这一指标去除打字过程中出现的错误字数比例,避免过去文献中出现的打字效率和错误率两项指标不统一的现象。经过试验人员的讲解和示范,受试者了解整个试验过程,签署知情同意书。
3 试验结果
受试者在适应性测试和正式测试阶段的打字效率分布如图2所示。多数受试者在不同阶段的作业效率保持一致,少数受试者在适应性测试或最后阶段出现了较大波动,这是因为适应性测试时受试者处于一个相对放松的状态,部分受试者尚未进入正常作业,而最后阶段接近试验结束,受试者在情绪上有所波动,并影响了打字效率。打字效率的最大差异主要体现在不同受试者之间,变化范围为22~90。不同阶段打字效率如图3所示。由图3可以看到,不同阶段打字效率均值表现出较好的平稳性,标准差的变动幅度也较小,说明在试验中受试者的打字效率主要受个体因素影响,在整个试验过程中受试者可以保持一定的打字效率,这一结论也与前述文献结果一致,即使用升降桌来实现站姿和坐姿交替办公对工作效率影响不大。
使用SPSS统计分析软件的重复测量方差分析方法检验不同试验阶段受试者打字效率的差异性,分析结果见表1。原假设各试验阶段的打字效率有显著性差异,显著性P值是用于判定假设结果的一个参数。P为0.198,因为P不等于0.01,未能满足球形度检验假设,且P大于0.05,所以应拒绝原假设[12],即各阶段的打字效率无显著性差异。因此,坐站交替的办公模式不对试验过程中打字效率波动产生显著性影响。此外,试验时间×性别的显著性P值也大于0.05,表明性别对打字效率的干扰较为轻微。
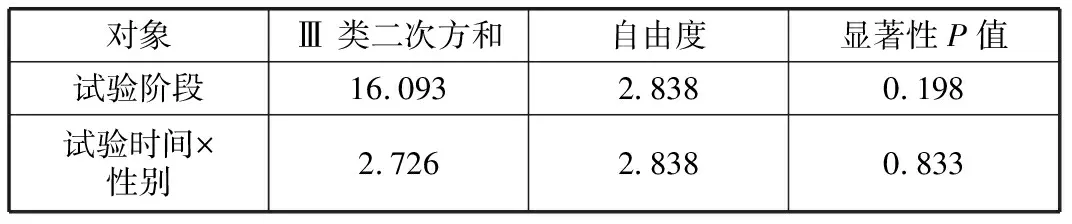
表1 不同试验阶段打字效率重复测量方差分析结果

▲图2 受试者打字效率分布

▲图3 不同阶段打字效率
4 岭回归分析
回归分析用于建立变量x与观测量y之间的映射关系,目的在于寻找最优假设函数来最好地拟合给定的x与y之间的关系[13]。目标函数J(ω)为:
J(ω)=∑(y-ωx)2
(1)
式中:ω为回归系数。
由上述分析可知,为了统一打字效率,将打字效率与准确率相结合,且打字效率为正式测试三个阶段的平均值,由此受试者的打字效率出现小数。受试者的打字效率多集中在40附近,舍弃小数会对误差造成累积。当矩阵元素中包含的小数位数过多时,对矩阵进行求逆、相乘操作会造成时间溢出。因此,先对数据进行预处理,利用标准化将数据按比例缩放,使之落入一个较小的特定区间。
标准化公式为:
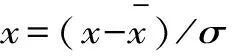
(2)
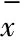
使用标准化可将数据划归至较小的范围内,除了能够减小不同量级特征对回归预测的影响,还可以提高迭代求解的收敛速度[13]。
通过试验获取数据,并进行统计。试验数据集为{(X1,Y1),(X2,Y2),……,(X20,Y20)},其中,Y1、Y2至Y20为各受试者正式测试三个阶段的平均值,X1、X2至X20为各受试者的数据集特征值,包含日均计算机使用时间、适应性测试打字效率、30 min站姿打字效率、45 min坐姿打字效率、15 min站姿打字效率共五个维度,多维样本特征值的设置可以避免回归方程与自变量共线的问题。
利用梯度下降法进行迭代更新求解参数,传统线性回归模型的迭代更新结果如图4所示,其均方根误差为0.071 61,迭代200次后达到最小值。
根据泰勒公式,任何函数都可以用多项式去逼近。当数据集的特征过多时,传统的线性回归会出现过拟合现象。在机器学习中,常用正则化来降低复杂度,减少过拟合。在目标函数中加入惩罚项,常用的惩罚函数为L1范数和L2范数,对应地称为L1正则化和L2正则化。L2正则化的作用是对原最优解的每个元素进行不同比例的放缩,可以保留所有特征,通过设置惩罚参数λ的大小,从而避免过拟合。在回归方程中加入L2正则化的约束即为岭回归,岭回归模型的目标函数J(β)为:
J(β)=∑(Y-Xβ)2+∑λβ2
(3)
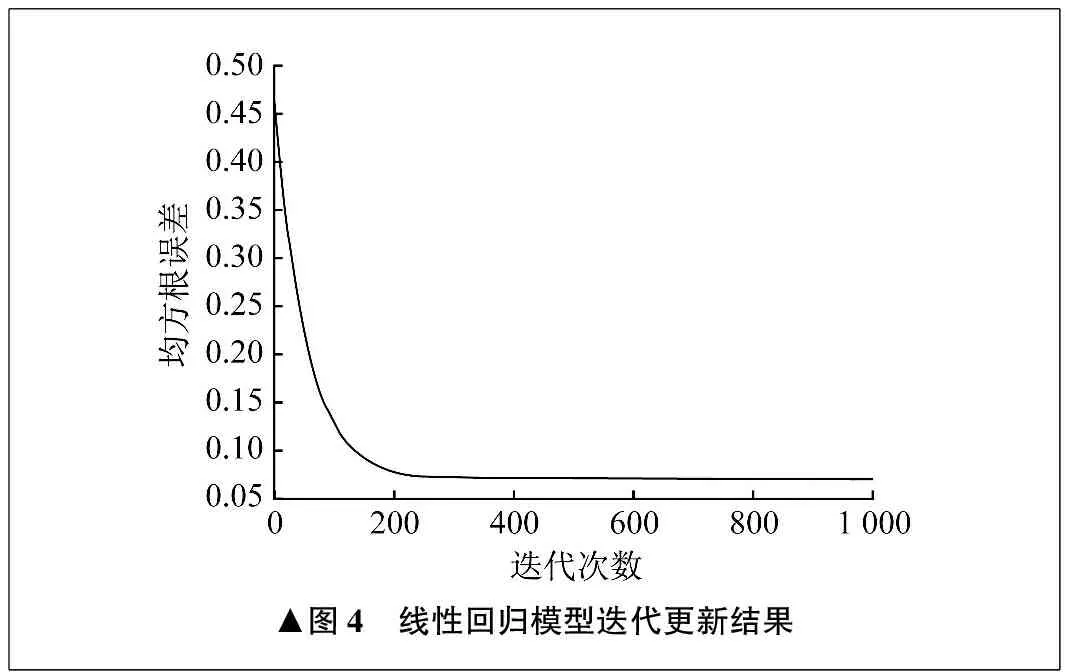
▲图4 线性回归模型迭代更新结果
式中:X为数据集特征值;Y为测试值;β为回归因数。
模型的方差可以用回归因数的方差来表征,测试值与预测值之间的偏差可以表示为模型的偏差,参数λ的选择需平衡模型的方差与偏差。
岭回归方程可以表示为:
Yn=β1Xn1+β2Xn2+…+βnXnn+φ
(4)
式中:n为样本总数;β1~βn为样本的特征因数;Xn1~Xnn为第n个样本的第1个至第n个特征;Yn为第n个样本的测试值;φ为常量。
式(4)的目标函数为:
(5)
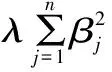
对式(5)进行最优参数求解,主要考虑梯度下降的方式,使目标函数沿当前点对应的梯度反方向按照预设的步长进行迭代,以求解极小值。梯度下降的公式为:
(6)
式(6)等号左侧设置为0,可以得到:
β=(XTX+λI)-1XTY
(7)
式中:I为单位矩阵。
随着λ的增大,|(XTX+λI)|增大,|(XTX+λI)|-1减小,回归因数的方差减小,真实值与输出值的偏差增大。使用岭回归进行回归分析的要点在于找到一个合适的λ。
Sklearn模块是机器学习中常用的第三方模块,对常用的机器学习方法进行了封装。从Sklearn模块中导入线性回归模型,然后采用10折交叉验证的方法,确定λ的值。当λ设置为1时,不改变学习率及迭代次数等参数,在引入标准化和正则化后,其均方根误差由0.071 61减小至0.061 73,减小了13.8%。岭回归迭代周期如图5所示,利用梯度下降法,由最初的迭代200次之后达到最小值,提升到迭代满100次之前达到最小值。
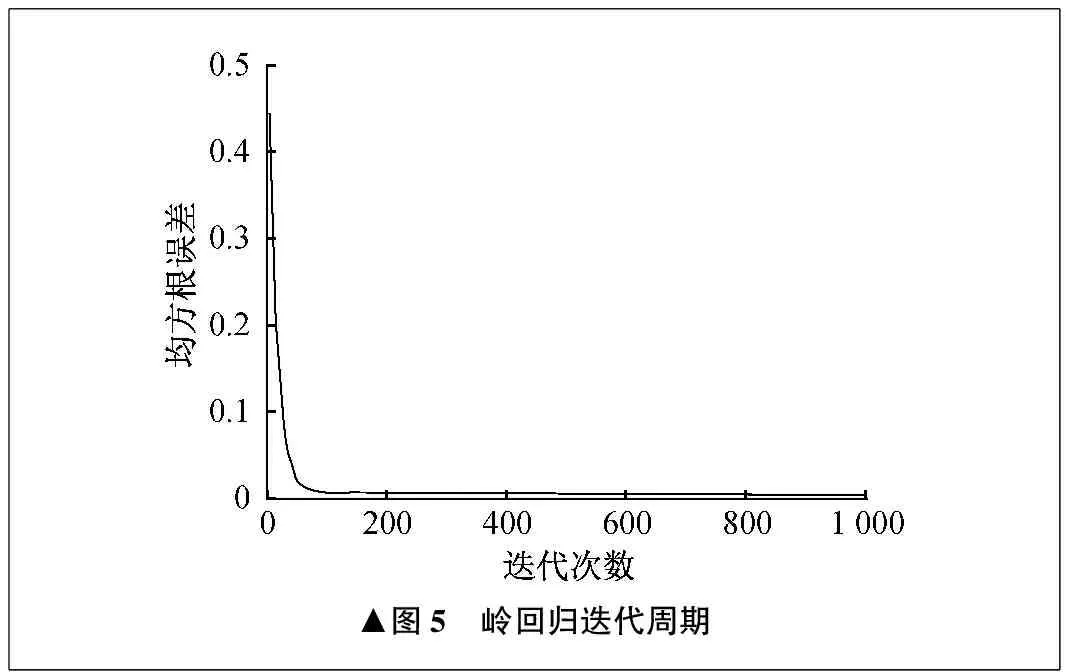
▲图5 岭回归迭代周期
一元线性回归又称单变量线性回归,在线性回归中引入最小二乘法,可以用于拟合变量之间的变化趋势[14]。作业效率回归图如图6所示。图6中的单变量回归分析显示,受试者在适应性测试与正式测试期间的打字效率皮尔逊相关因数为0.92,表现出两者高度的线性相关性,表明适应性测试的表现可以基本定性不同受试者打字效率的差异性。由上述分析可知,受试者坐姿阶段打字效率对于最终打字效率的影响比重高于站姿阶段。经过90 min的坐站交替模式后,打字效率没有下降,说明坐站交替模式对保持工作积极性具有一定的作用。
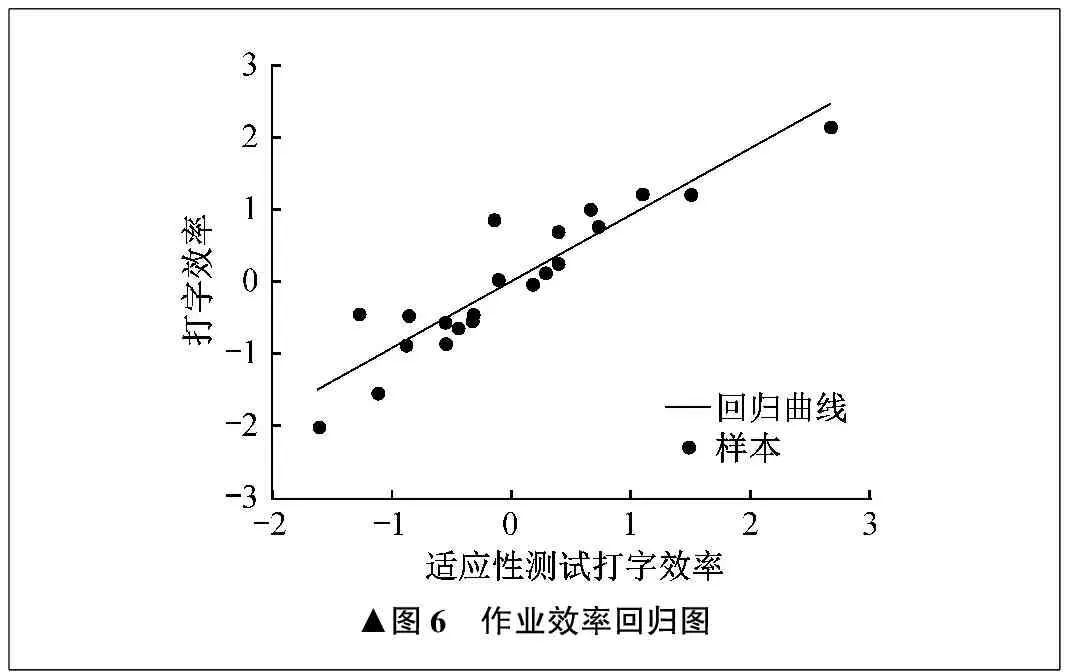
▲图6 作业效率回归图
5 结束语
针对坐站交替工作模式的研究表明,久坐办公环境下引入站姿作业,打字效率在试验的不同阶段未表现出显著性差异,性别因素在试验的不同阶段影响也相对较弱,但不同受试者之间的差异较为明显。
在回归分析中引入标准化和正则化,不仅可以减少梯度下降所需要的迭代次数,而且减小了均方根误差,表明岭回归在回归问题分析中具有较好的鲁棒性和时效性。
