数控机床主轴系统可靠性分析*

□ 金 城 □ 高 通 □ 怀天澍 □ 杨胜康

1.上海航天精密机械研究所 上海 2016002.西安电子科技大学 机电工程学院 西安 710071

1 分析背景

可靠性是机械零部件的一个重要质量指标特征,受工况、零部件尺寸、安装精度、材料参数等不确定因素影响。20世纪70年代初,苏联首先开展了机床可靠性研究,形成了机床可靠性基础理论。20世纪80年代,美国也大力开展机床可靠性分析研究。我国在20世纪80年代末开始数控机床可靠性研究。机床可靠性是国内外学者研究的热点,主轴系统作为数控机床的核心部件之一,研究从未止步。目前,国内外针对数控机床主轴系统的可靠性做了大量研究。张鹏[1]运用故障树分析与故障模式、影响及危害性分析方法分析了数控机床主传动系统的可靠性。张李铁等[2]采用故障模式、影响及危害性分析方法,确定了数控机床主轴系统的故障模式和原因,为数控机床的维修策略提供了参考。籍永建等[3]对机床主轴常见的故障模式进行了分析,并提出了提高主轴可靠性的措施。秦少军等[4-5]对主轴可靠性的影响因素进行了分析,建立可靠性数学模型进行主轴系统可靠性预测。李兆军等[6]基于有限元法建立电机组主轴系统的非线性动力学方程,采用可靠性理论及模糊理论构建振动可靠性模糊模型。刘征[7]针对重型数控机床,基于不精确概率理论的混合不确定性统一量化框架,对机床的零部件进行考虑多失效模式相关性的可靠性建模与分析。王德超等[8]采用模糊综合评判法进行分析,求得机床主轴系统的危害度,并对主轴系统进行了可靠性评价。胡军[9]根据可靠性分析理论,运用有限元分析软件的概率设计功能,对数控导轨磨床的主轴进行可靠性分析。刘智键等[10]针对机床主轴的可靠性预测需求,提出一种基于蒙特卡洛模拟法的机床主轴可靠度求解方法,有效进行机床主轴的可靠性预测。以上学者围绕可靠性分析方法、机床主轴系统可靠性分析、主轴系统失效形式等做了大量研究,并取得了许多重要研究成果,但是针对机床主轴系统的可靠性建模大多是基于数据的,当获得的数据较少或无法获得数据时,针对主轴系统可靠性建模的研究则较少。笔者将改进一次二阶矩法与克里金重要度抽样方法相结合,提出基于改进一次二阶矩法和克里金重要度抽样方法的考虑主轴轴承动态磨损过程的数控机床主轴系统可靠性分析方法,提高了数控机床主轴系统可靠度的计算效率。

2 改进一次二阶矩法

改进一次二阶矩法又称设计验算点法,以功能函数的线性化泰勒展开点为设计点,该点位于功能函数的失效面上,从根本上解决了一次二阶矩存在的问题。

假设结构的极限状态方程为:

Z=gx(X)=0

(1)

式中:gx(X)为功能函数;X为基本随机向量。

Z>0,结构处于可靠状态。Z<0,结构处于失效状态。Z=0,结构处于极限状态。

假设x*为极限状态面上的一点,在x*点处依据泰勒级数展开并取一次项,有:

Z=gx(x*)=0

(2)

(3)

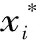
基于符合相互独立正态分布随机变量具有线性组合的性质,展开式ZL的均值μZL与标准差σZL分别为:

(4)

(5)

式中:σXi为Xi的标准差。

可靠度指标β为:

(6)

(7)

(8)

式中:Yi为Xi的标准化变量。

基于变量灵敏度因数的方程式为:

(9)

(10)

可靠度指标的几何意义及设计点如图1所示。在标准正态空间内,公式(10)为随机变量的法线式超平面方程,其长度即为可靠度指标β。极限状态面上的点x*即为设计点[11]。

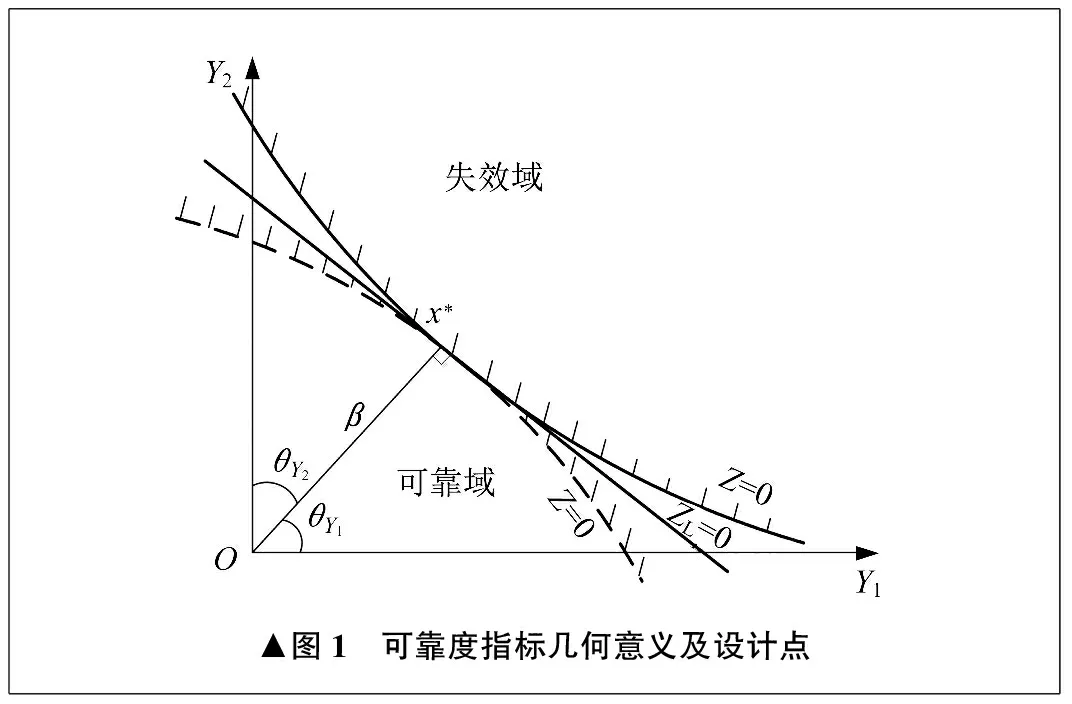
▲图1 可靠度指标几何意义及设计点

设计点x*在标准正态空间中可以表示为:

(11)

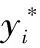
将设计点转换到原始空间中,有:

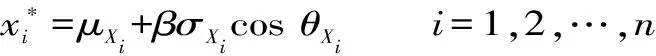
(12)

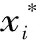
根据上述分析,经反复迭代求解,直至求得满足迭代要求的可靠度指标。结构的可靠度R为:

R=φ(β)

(13)

式中:φ为标准正态分布函数的累积分布函数。

3 克里金模拟方法

克里金模拟方法是一种改进的线性回归分析技术,由线性回归部分和非参数部分两部分组成,具体模型为:

g(x)=F(β1,x)+z(x)=f(x)Tβ1+z(x)

(14)

式中:g(x)为输出响应;F(β1,x)为变量β1、x的多项式;f(x)T为变量x的多项式;β1为回归因数;z(x)提供模拟局部偏差的近似。

z(x)是均值为零的平稳高斯过程,但是该高斯过程的协方差不为零,即z(x)同分布不独立,空间内任意两点x、w的协方差为:

(15)

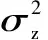
高斯相关函数的计算效率较高,而且其应用范围是最广泛的。高斯相关函数为:

(16)

式中:xi和wi为空间内任意两点x、w的第i个分量;θi为相关性参数;δi为光滑程度参数,一般取2,表示相关方程式无限可微。

给定训练样本[x(1),x(2),…,x(p)],x(i)是R域上的第i个样本点,训练样本点的响应为:

Y=[y1,y2,…,yp]

(17)

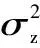
(18)

(19)

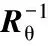
(20)

克里金模型确定之后,可以通过确定的模型预测未知点的响应。假定样本点为x,基于已经确定的模型,可以估计出新样本的响应值。克里金预测值的计算公式如下:

(21)

(22)

(23)

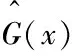
克里金模拟方法是一种精确的插值方法,任意已知训练点x(i)的预测值G(x(i))是准确的,即:

(24)

4 结构可靠性分析

结构失效属于小概率事件,对小概率事件进行评估是比较困难的。结构的功能函数越复杂,就越能反映真实结构在随机变量下的响应,但是复杂的功能函数会导致计算效率下降。针对以上难点,笔者提出克里金重要度抽样方法,将克里金插值与克里金重要度抽样方法相结合,基于已知信息及克里金模拟方法建立的插值模型来对结构的响应进行模拟,所需的评估模型通过少量训练样本即可确定,对未知样本点的结构响应预测的准确度比较高。克里金重要度抽样方法流程图如图2所示。

(1) 基于改进的一次二阶矩迭代求解状态方程的设计点。

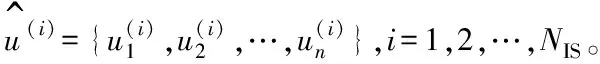
(3) 初始数值试验设计。这一步骤的主要目的是确定克里金模型的训练样本。为了减少模拟过程中的计算量,将步骤(1)计算设计点过程中产生的样本和对应的功能函数值作为初始训练样本及对应的结构响应。

(4) 基于数值试验设计建立克里金模型。DACE工具箱是应用于软件的克里金工具箱,被广泛应用于克里金模型建立及分析中。本方法基于已知的训练样本及对应的结构响应,采用DACE工具箱建立克里金模型。

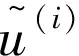
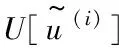
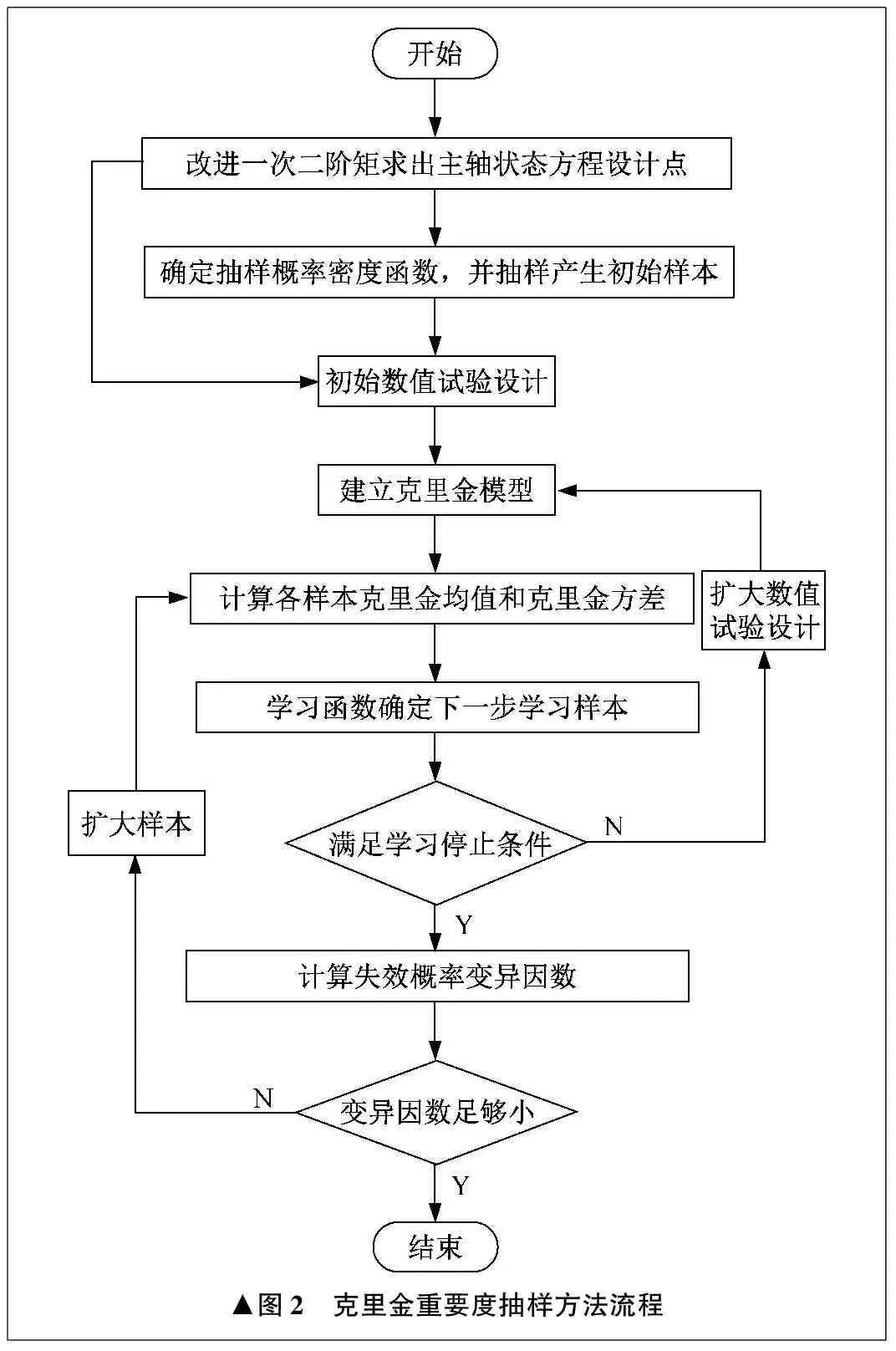
▲图2 克里金重要度抽样方法流程

(7) 学习停止条件。通过设置合理的学习停止条件来保证克里金模型的有效性。定义使学习函数最小的那个样本对应的U值大于等于2时,学习停止,此时表示将所有样本正确分在安全域和失效域的概率大于97.7%,即结构失效概率可靠度为97.7%。

(8) 扩大数值试验设计。若步骤(7)中的学习停止条件不满足,则将学习函数值最小的那个样本增加到数值试验设计中,然后基于新生成的训练样本点重新训练克里金模型,直至步骤(7)中的学习停止条件满足。

(9) 计算失效概率变异因数。若步骤(7)中的学习停止条件满足,表明在步骤(2)中生成的样本量下计算出了满足学习条件的失效概率,但是该样本量是否已经足够大,所得到的结构失效概率是否可靠,仍需探讨,同时计算预测的失效概率变异因数。

(10) 更新样本群。为了保证通过克里金预测的结构失效概率是可靠的,若计算的失效概率变异因数过大,则需要增加样本数量。基于步骤(3)训练的克里金模型,对更新后的样本计算克里金均值及克里金方差,直至失效概率变异因数足够小。此时,通过克里金预测的结构失效概率即为最终的结果。

5 应用实例分析

笔者采用某型号数控机床主轴系统作为应用实例研究对象,其主轴结构如图3所示。主轴系统采用的角接触球轴承型号为7210B,具体参数见表1。采用MATLAB软件进行仿真计算。

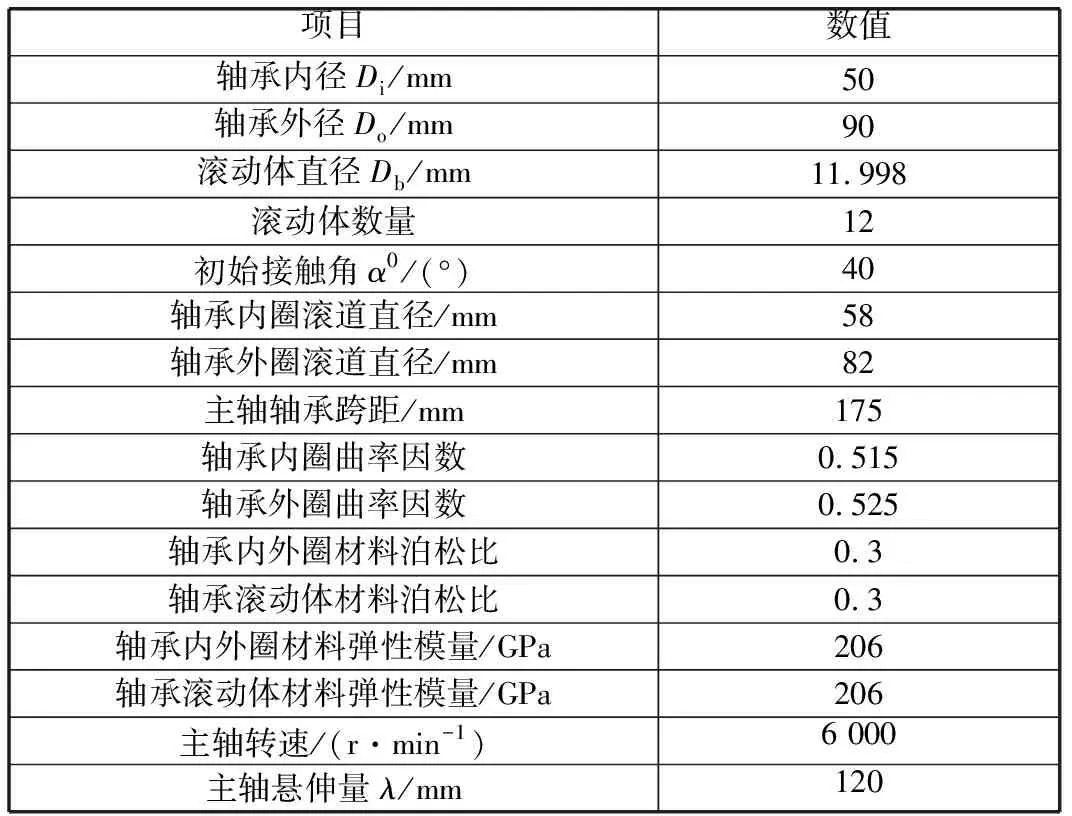
表1 角接触球轴承参数

建立主轴系统的功能函数为g(u):

g(u)=0.001-Δ′

(25)

式中:Δ′为由磨损引起的主轴轴端径向跳动。

该精密数控机床主轴系统允许的最大径向跳动为0.001 mm。

经分析,确定主轴系统可靠性功能函数的随机变量为:

uT=[Db,Di,Do,α0,λ]

(26)

通过计算及查阅相关资料,获取各随机变量的均值,根据公差标准确定各几何尺寸的标准差。主轴系统各随机变量均值与标准差见表2。

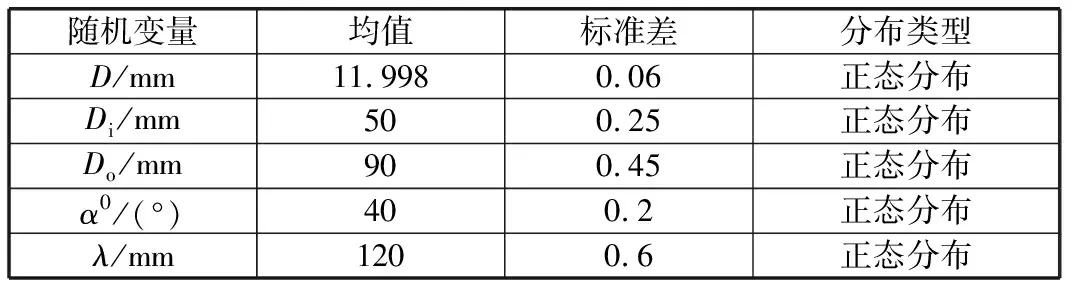
表2 主轴系统各随机变量均值及标准差

针对可靠性功能函数,基于表2,采用改进一次二阶矩法和克里金重要度抽样方法计算主轴系统可靠度,并与蒙特卡洛模拟法进行对比,可靠度及失效率曲线分别如图4、图5所示。蒙特卡洛模拟法与克里金重要度抽样方法可靠度计算结果对比见表3。

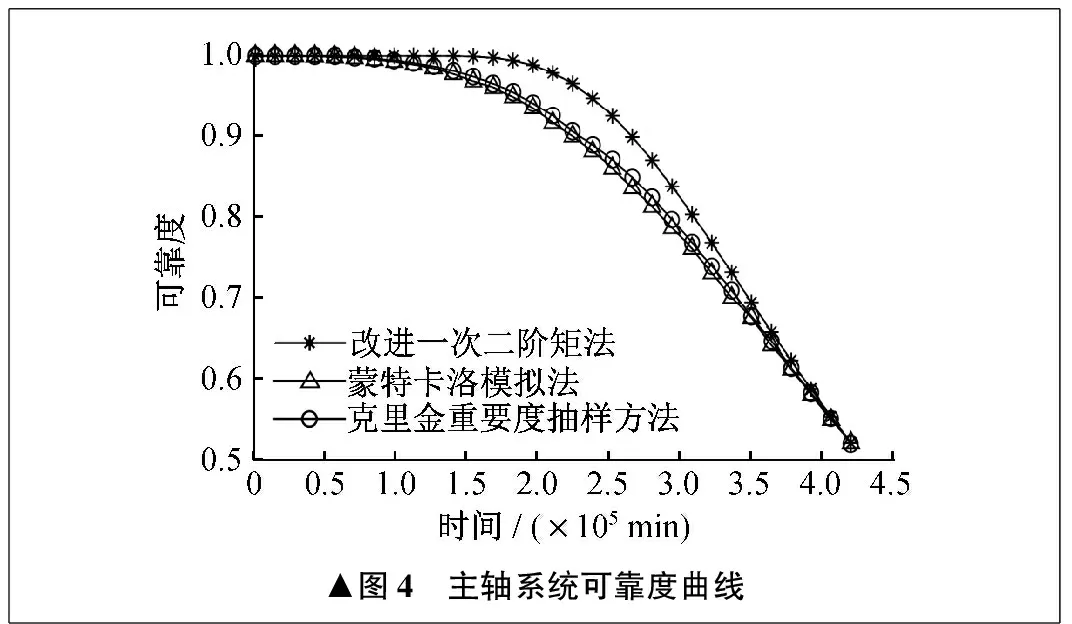
▲图4 主轴系统可靠度曲线

▲图5 主轴系统失效率曲线

由图4、图5、表3可以看出,主轴系统随着服役时间的推移,可靠度呈现出不同的状态。0时刻时,主轴系统的可靠度为1。当服役时间小于1×105min时,主轴系统的可靠度曲线较为平稳,主轴系统的可靠度变化不大。当服役时间为4.2×105min时,可靠度降为0.52。

表3 主轴系统可靠度计算结果对比

克里金重要度抽样方法与直接蒙特卡洛模拟法的计算结果误差不大,表中给出的结果中最大误差产生于服役时间为2.94×105min时,计算误差为1.36%,但是克里金重要度抽样方法的抽样次数远少于蒙特卡洛模拟法,即采用克里金重要抽样度方法计算主轴系统可靠度时,具有较高的计算效率。

根据图4及图5可得,主轴系统的可靠度随着服役时间的推移不断降低。随着轴承磨损量的增大,引起主轴系统轴端径向跳动量呈增大趋势,导致主轴系统向性能退化方向发展,从而表现出主轴的可靠度呈不断下降趋势。在分析过程中,没有考虑主轴零件的缺陷、工艺及质量控制等其它失效形式,仅对轴承疲劳磨损引起的主轴轴端径向跳动进行分析,因此主轴系统的失效率曲线具有浴盆曲线中后半段的特性。

6 结束语

笔者为提高计算效率,将克里金重要度抽样方法与克里金模拟方法相结合,提出了基于克里金重要度抽样方法的数控机床主轴系统可靠性分析方法。将计算结果与蒙特卡洛模拟法、改进一次二阶矩法的计算结果进行比较,结果表明,基于克里金重要度抽样方法计算主轴系统的可靠度,效率明显提高,主轴系统的可靠度随着服役时间的推移而下降。