单面柱局域共振声子晶体低频带隙特性分析及结构改进研究
2021-08-23孙向洋郭翔鹰
孙向洋,燕 群,郭翔鹰
(1.中国飞机强度研究所,航空声学与动强度航空科技重点实验室,西安 710065;2.北京工业大学机械工程学院,机械结构非线性振动与强度北京市重点实验室,北京 100124)
0 引 言
声子晶体是指由两种或者两种以上不同力学性能的材料构成的周期结构功能材料,由于这种结构或者材料的周期性,某些特定范围频率的弹性波无法在其中传播,该频段范围称为声子带隙[1-2]。声子带隙产生的机理有两种:布拉格散射机理和局域共振机理。布拉格散射型声子晶体[3],特点为弹性波在该周期结构内部的传播出现相互干涉,导致其传播受阻,表现出无法传播的现象。局域共振型声子晶体[4],特点为在特定频率的弹性波激励下,各个散射体产生共振,并与弹性波长波行波相互作用,从而抑制弹性波的传播。
自从2000年刘正猷教授提出局域共振声子晶体概念以来,有关局域共振声子晶体的研究日益增多[5-8],局域共振声子晶体产生带隙的物理机理不同于布拉格散射,它是由局域共振单元的强共振特性决定的,因此具有显著不同的带隙特点,带隙特性的影响因素也有所不同。局域共振型声子晶体用较小的尺寸获得较低频带隙[9],这一特点为声子晶体在低频减振降噪方面的应用提供了新的思路,具有重要的理论价值和应用前景,例如用于隔振减振、隔声降噪、制作声波滤波器、隔振器和波导装置等[10-15]。
国内外学者也对局域共振声子晶体结构进行了大量研究,主要集中在研究弹性波在声子晶体结构中的传播特性[16]。例如,Goffaux等[17]用数值方法研究了弹性波在一种局域共振声子晶体(将重圆柱嵌入软聚合物当中,并将它们用刚性网格相连接)中的传播。Gu等[18]研究了二维声子晶体中弹性波的共振模式及对弹性波传播的影响。Yao等[19]采用有限元法研究了在环氧树脂基板两侧布置软橡胶形成的局域共振声子晶体条形波导结构中兰姆波的能带结构。Wang等[20]提出了一种双分量局部共振结构,发现其中一个带隙是由与散射单元相关的共振频率引起的,这个频率范围比通常的布拉格带隙要低近两个数量级,而且局部共振频率不仅取决于几何形状,还取决于散射体与基体的密度比。Hsu等[21]应用Mindlin理论,利用平面波展开公式研究了二维二元局部共振薄声子平板中的兰姆波带隙。
对于局域共振声子晶体结构,能带结构的求解是其重要的研究内容之一,目前声子晶体带隙特性计算方法主要有传递矩阵法、平面波展开法、时域有限差分方法、多重散射法、有限元法等[22-23]。这些方法各有利弊,传递矩阵法可以计算一维声子晶体解析的色散关系和传输系数,但是不能直接处理二维和三维声子晶体[1];平面波展开法思路清晰,可以适用二维和三维声子晶体,但是当组元材料参数差异较大时,收敛缓慢[24];时域有限差分方法可计算较为复杂的模型,并直接进行时域计算,但是存在稳定性问题[25];多重散射法理论推导较为复杂,且只能用于简单的圆柱及球形散射体单元结构的声子晶体[26];有限元法适用范围广泛,不但能直接计算声子晶体的能带结构[27],也可快速计算其传递损失。
综上所述,本文采用有限元法对单面柱局域共振声子晶体进行带隙特性分析,研究了结构参数对于该类型声子晶体的影响情况。并且在经典单面柱声子晶体的基础上,组合了两种新型的三组元单面柱声子晶体结构Ⅰ和结构Ⅱ,并对其带隙特性进行分析。
1 模型介绍
由于晶体的周期性,对于理想的无限周期的声子晶体只需要研究一个单胞即可[28]。取文献[28]中的单面柱声子晶体单胞模型作为经典单面柱声子晶体模型,结构Ⅰ和结构Ⅱ均为在此基础上的改进结构。单胞的基体底面边长为a,基体厚度e,散射体高度h,散射体半径r,基体所用材料为橡胶,散射体所用材料为钢,材料参数如表1所示。

表1 材料参数
结构Ⅰ和结构Ⅱ如图2和图3所示,结构Ⅰ是将经典的单面柱声子晶体与含包覆层声子晶体相结合,将散射体嵌入基板中,同时在散射体与基板中间加入一层包覆层;结构Ⅱ是直接在散射体与基板中间添加一种新的材料进行粘接组成。结构Ⅰ基体底面边长为a,基体厚度e,散射体高度h,散射体半径r,基体所用材料为铝,散射体所用材料为钢,包覆层圆环的厚度为1 mm,材料为橡胶。结构Ⅱ基体底面边长为a,基体厚度为e,高度h1=h2=5 mm,材料A为钢,材料B为橡胶,基板仍然为铝。各材料参数如表1所示。
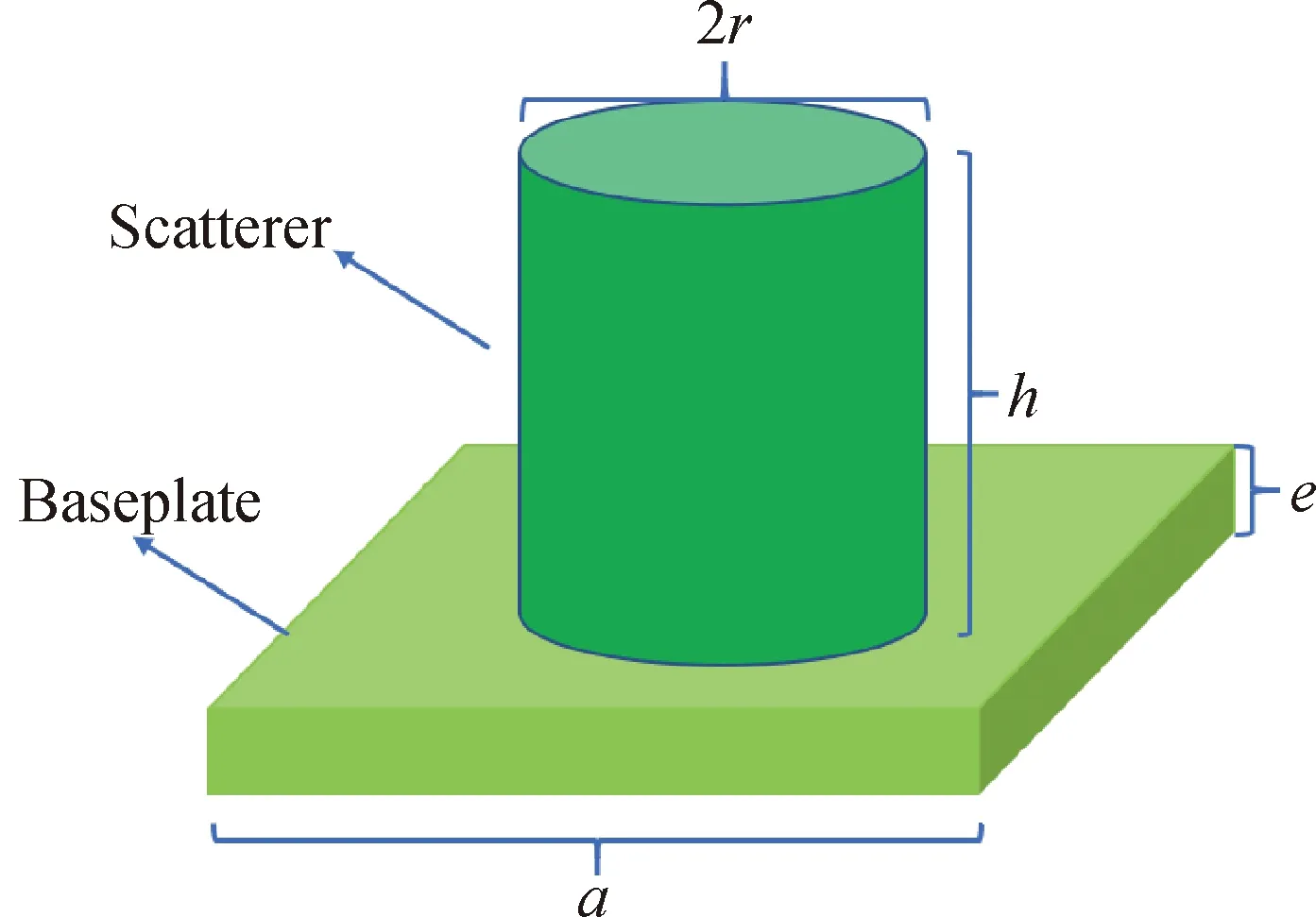
图1 声子晶体单胞模型
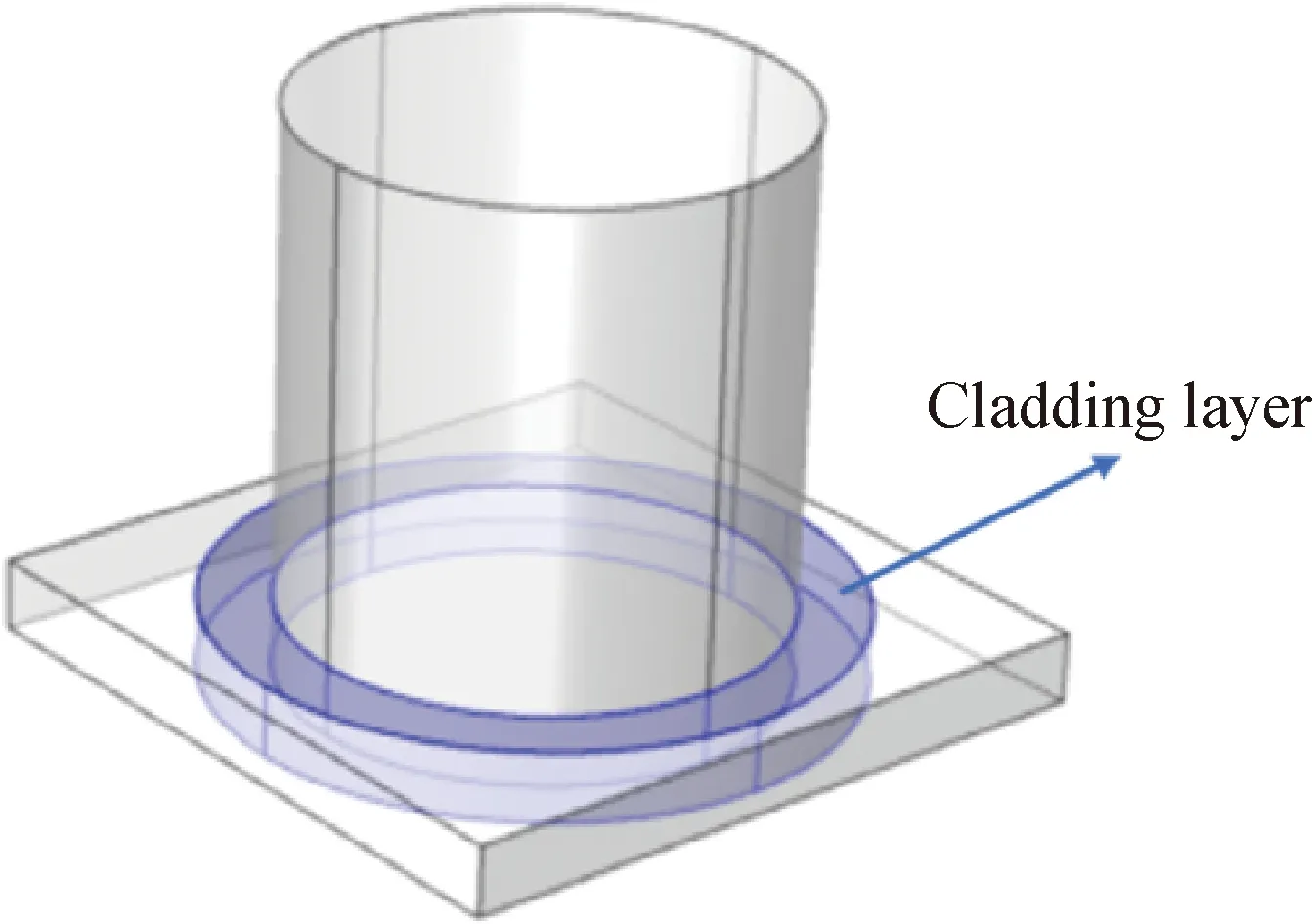
图2 结构Ⅰ
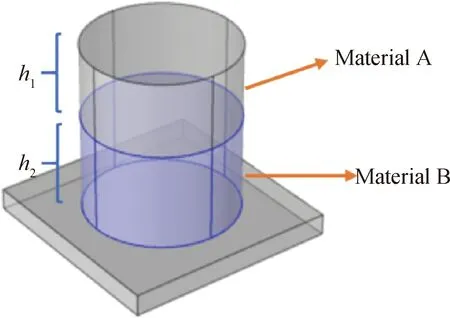
图3 结构Ⅱ
2 有限元简介
采用商业有限元分析软件 COMSOL Multiphysics 求解弹性波在声子晶体中的波动方程。由于晶体的周期性,依照Bloch定理,对于理想的无限周期的声子晶体只需要研究一个单胞即可。进行网格划分后,根据单胞的离散特征方程形式,由结构的周期性可得:
(1)
式中:格矢R的格点为正格矢;矢量G的格点为倒格矢,e为基体厚度。
根据Bloch定理,在周期场中的本征函数形式为:
(2)
为了得到声子晶体的能带曲线,对于正方晶格,只需要波矢k在不可约Brillouin区的边界遍历取值即可。
3 结果与讨论
3.1 单面柱局域共振声子晶体板低频带隙特性分析
对于经典的单面柱局域共振声子晶体进行带隙特性分析,在已有的文献研究的基础上,已经明确了材料参数对于其带隙的影响效果[28],本文进一步分析结构参数对于该声子晶体的影响情况。
3.1.1 与现有文献结果的对比验证
首先将本节的计算结果与已有文献[28]的计算结果进行对比,验证本文计算方法的正确性。声子晶体单胞的基体底面边长a=10 mm,基体厚度e=2 mm,散射体高度h=10 mm,散射体半径r=4.5 mm,基体所用材料为橡胶,散射体所用材料为钢。
计算结果如图4所示,从计算结果可以得出:本节计算的结果与文献中的结果具有高度的一致性。据此可得,本章模型计算方法是正确合理的。

图4 能带结构计算结果对比
3.1.2 结构参数对单面柱声子晶体的影响
材料参数对于单面柱声子晶体带隙特性的研究已经明确,材料的密度和杨氏模量都会对带隙产生明显的影响[28]。但是结构参数对于该声子晶体的带隙影响情况还未明确。因此,下面针对结构参数对单面柱声子晶体的影响情况进行研究。
首先研究散射体高度对带隙的影响情况,取声子晶体单胞的基体底面边长a=10 mm,基体厚度e=2 mm,散射体高度h分别从1~15 mm,步长为1 mm的变化,散射体半径r=4.5 mm,基体材料为橡胶,散射体材料为钢。计算出该声子晶体的第一完全带隙随着散射体高度的变化情况如图5所示。

图5 第一完全带隙与散射体高度的关系
从图5计算的结果得出,随着散射体高度的增加,单面柱声子晶体的第一完全带隙的起始频率逐渐降低。但是降低的幅度逐渐减小,截止频率变化不大,带宽逐渐增大。为了达到低频宽带的目的,可取散射体的高度为10 mm。
进一步研究基板的厚度对带隙的影响情况,同样取声子晶体单胞的基体底面边长为a=10 mm,基体厚度e分别从1~10 mm,步长为1 mm取值,散射体高度h=10 mm,散射体半径r=4.5 mm,基体所用材料为橡胶,散射体所用材料为钢。计算出该声子晶体的第一完全带隙随着基板厚度的变化情况如图6所示。
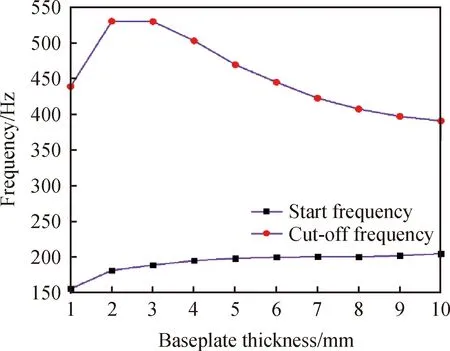
图6 第一完全带隙与散射体基板厚度的关系
从图6中的计算结果可以得出,随着基板厚度的增大,单面柱声子晶体的起始频率逐渐升高,截止频率先增大后减小。由于在基板厚度取1 mm附近的规律与其他区域不同,所以进一步分析基板厚度取0.1~1 mm,步长为0.1 mm的变化,计算结果如图7所示。计算结果得到,在基板厚度处于2 mm以内时,随着基板厚度的增加,声子晶体的第一带隙的起始频率、截止频率以及带宽都逐渐增大。因此为了达到低频宽带的目的,可选取基板厚度为2 mm。
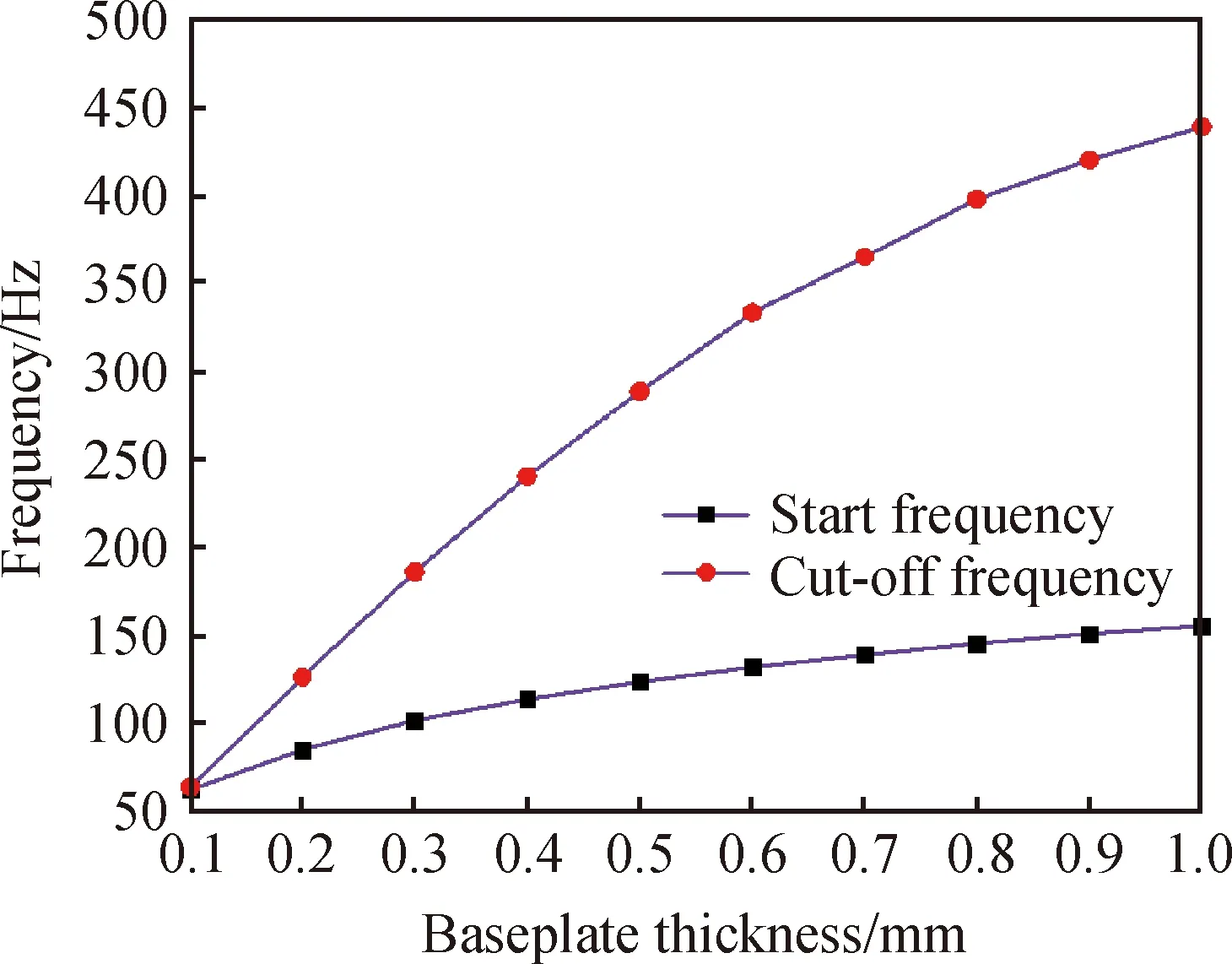
图7 第一完全带隙与散射体基板厚度的关系
3.2 单面柱局域共振声子晶体的结构改进研究
3.2.1 改进型结构的能带计算
本节首先分析两种改进型结构的色散关系,并与经典单面柱结构进行对比。对于经典单面柱声子晶体,取声子晶体单胞的基体底面边长a=10 mm,基体厚度e=2 mm,散射体高度h=10 mm,散射体半径r=3.5 mm,基体所用材料为铝,散射体所用材料为钢。结构Ⅰ包覆层圆环的厚度为1 mm,材料为橡胶,其他参数与经典单面柱声子晶体相同。结构Ⅱh1=h2=5 mm,材料A为钢,材料B为橡胶,基板仍然为铝,其他参数与经典单面柱声子晶体相同。
图8给出了三种结构的能带曲线计算结果,表2是它们对应的第一完全带隙范围的计算结果。由结果可知,改进后的结构Ⅰ和结构Ⅱ均能在较低的频率内获得带隙,结构Ⅰ在301 Hz就能出现带隙,结构Ⅱ在169 Hz出现带隙,然而经典单面柱结构则需要在85 564 Hz才会出现带隙。通过对比发现,改进后的两种结构相对于经典的单面柱结构具有产生更低频带隙的优势,而低频隔振降噪正是目前亟待解决的问题,所以改进后的结构具有更大的应用前景与研究价值。

图8 三种不同结构能带曲线计算结果

表2 三种声子晶体结构第一完全带隙能带结果比较
3.2.2 包覆层厚度对结构Ⅰ的影响
在改进型结构Ⅰ中,包覆层的引入对于声子晶体的带隙产生了明显的影响,因此本文研究该包覆层的厚度对于结构Ⅰ声子晶体的带隙影响情况。取声子晶体单胞的基体底面边长a=10 mm,基体厚度e=1 mm,散射体高度h=10 mm,散射体半径r=3.5 mm,基体所用材料为铝,散射体所用材料为钢,包覆层为橡胶,包覆层圆环的厚度分别从0.5~1.4 mm,步长为0.1 mm的变化。计算第一完全带隙与包覆层厚度的关系,结果如图9所示。从计算结果得出,随着包覆层厚度的增加,第一带隙的起始频率和截止频率均降低,带宽逐渐变大。所以本着低频宽带的原则,结构Ⅰ的包覆层厚度可尽量增大一些,但是要注意包覆层的直径不能大于基板底面正方形的边长。
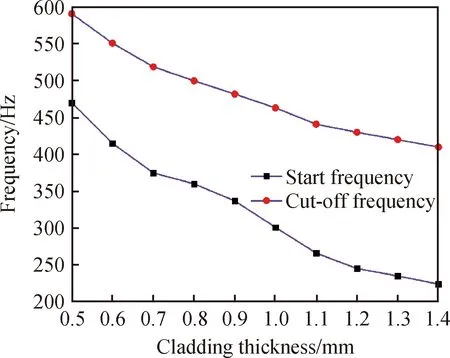
图9 第一完全带隙与结构Ⅰ包覆层厚度的关系
3.2.3 散射体高度对结构Ⅱ的影响
在改进型结构Ⅱ中,材料B的引入,将散射体分为两个部分,由于材料B的引入对于声子晶体的带隙产生了明显的影响,因此本文研究当h1+h2=10 mm固定的时候,h2变化会对结构Ⅱ声子晶体的带隙影响情况。取声子晶体单胞的基体底面边长a=10 mm,基体厚度e=1 mm,散射体高度h1+h2=10 mm,h2分别从1~9 mm,步长为1 mm的变化,散射体半径r=3.5 mm,基体所用材料为铝,材料A为钢,材料B为橡胶。计算第一完全带隙与h2高度的关系,结果如图10所示。计算结果表明,当h2太小时不存在带隙,当h2>2 mm,随着h2的增加,结构Ⅱ声子晶体的第一带隙起始频率和截止频率都是先减小后增大的。当h2=4 mm时,带隙的起始频率最低为170 Hz。因此本节研究的结构Ⅱ型声子晶体结构的最佳h2高度为4 mm,此时得到最低频率的带隙。同时对于结构Ⅱ型声子晶体最低频带隙出现在h2取中间值附近。
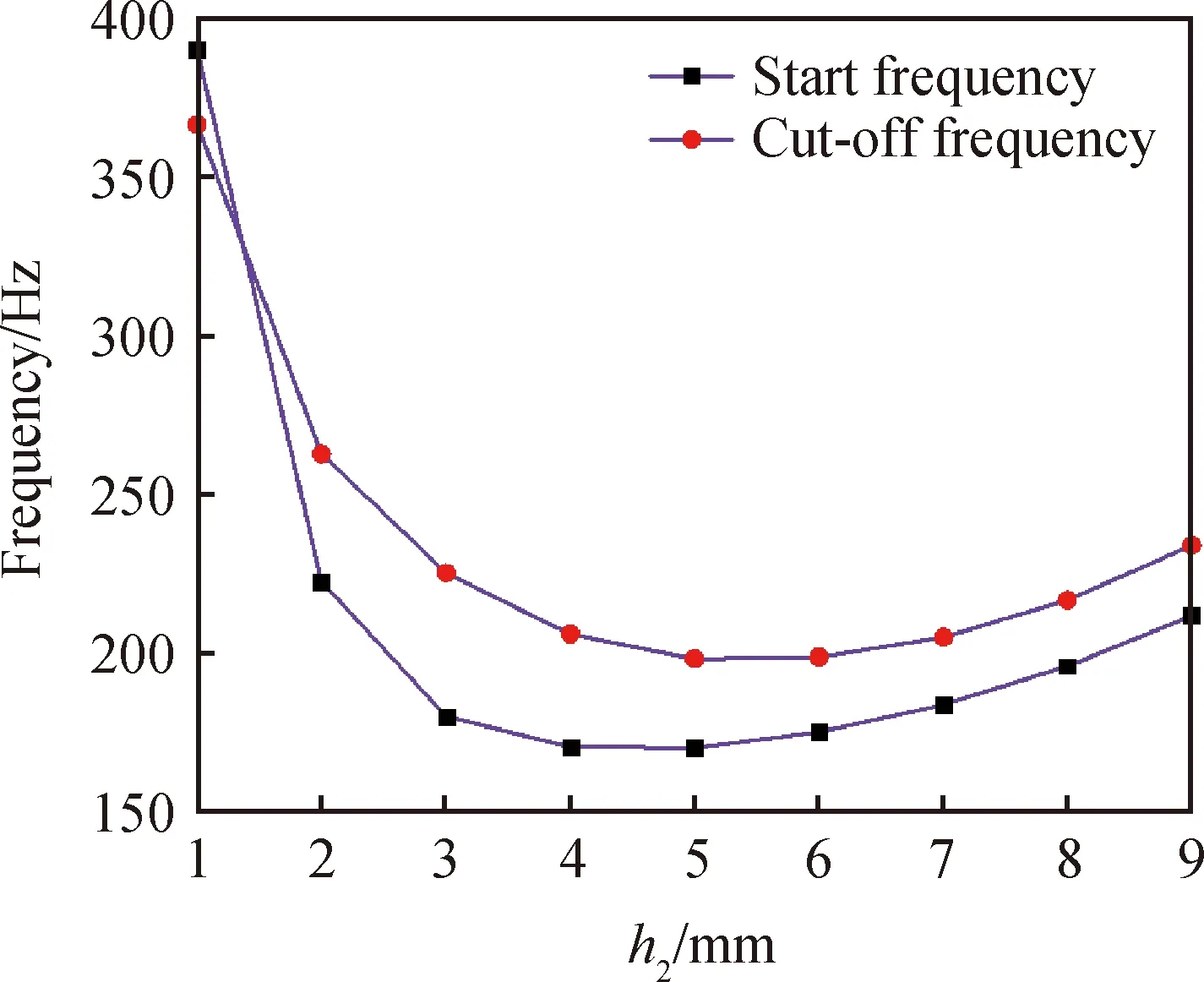
图10 第一完全带隙与结构Ⅱh2高度的关系
3.2.4 材料A的半径对结构Ⅱ的影响
考虑到对于传统的声子晶体其填充率对声子晶体的带隙影响较为明显,因此针对结构Ⅱ,有必要研究其散射体材料A的半径对其带隙的影响情况。取声子晶体单胞的基体底面边长为a=10 mm,基体厚度e=1 mm,散射体高度h1=h2=5 mm,圆柱体材料B半径R2=3.5 mm,材料A半径R1分别从2~5 mm,步长为0.5 mm的变化,基体所用材料为铝,材料A为钢,材料B为橡胶。计算第一完全带隙与R1大小的关系,结果如图11所示。
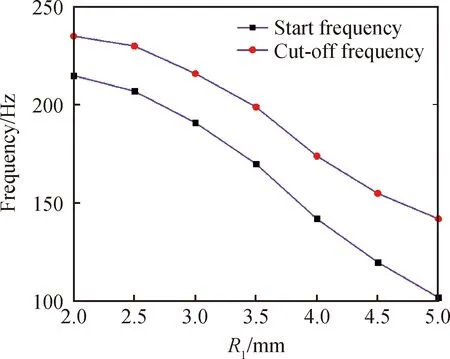
图11 第一完全带隙的与结构ⅡR1大小的关系
从计算结果可以得出,随着R1的不断增大,结构Ⅱ声子晶体的带隙起始频率和截止频率均向低频移动。因此对于这种结构的声子晶体,将R1扩大是很有利于低频隔振降噪的,但是需要注意R1不能大于基板单胞边长a的一半。
4 结 论
本文首先介绍了经典单面柱声子晶体的结构形式,并将计算的结果与文献进行对比验证了本文计算方法的正确性,然后分析经典的单面柱声子晶体结构参数的影响。在此基础上,组合出了两种新型的单面柱局域共振声子晶体结构,并分别进行带隙计算,得到以下结论:
(1)发现这两种新结构与经典的单面柱声子晶体相比,都具有更低频的带隙。
(2)对结构Ⅰ分析了包覆层厚度对其带隙的影响情况,发现随着包覆层厚度的增加,第一带隙的起始频率和截止频率均降低,带宽逐渐变大,所以结构Ⅰ的包覆层厚度增大可降低禁带频率,但是包覆层的直径不能大于基板底面正方形的边长。
(3)对结构Ⅱ分析了h2高度对其带隙的影响,发现对于结构Ⅱ型声子晶体最低频带隙出现在h2中间取值附近。
(4)这两种新型的单面柱声子晶体结构都能在更低的频率出现带隙,这为低频减振降噪方面的应用提供了新的思路,具有一定的理论价值和应用前景。
