基于人工微纳结构的平板衍射透镜

何 俊，黄 坤，庄继成

(1.中国科学技术大学物理学院，光学与光学工程系，合肥 230026；2.黄山精工凹印制版有限公司，黄山 245900)

0 引 言

如今，光学显微镜已经广泛运用于研究和工业等领域。自其被发明以来，提升其成像质量和分辨率一直具有重要的研究价值和现实意义。由于衍射的存在，光学显微镜在可见光波段范围内的空间分辨率被限制在200 nm左右，这已经由Abbe[1]和Rayleigh[2]通过经典光波理论进行了明确地阐述，量子力学中的不确定关系也能佐证这一事实[3]。随着纳米技术的迅速发展，光学显微镜的有限分辨率无法满足生物成像、材料科学以及纳米光刻等领域的需求。为突破该衍射极限，数十年来人们在发展各种超分辨率技术方面付出巨大努力。这些技术大致可以分为三类：近场、远场荧光标记法和远场无标记法。

傅里叶光学中，一个物体可以看成具有不同空间频率平面波的加权叠加[4]。当物体被入射光照明后，物体的散射光包括空间频率小于1/λ的传播波和空间频率大于1/λ的倏逝波。传统光学显微镜仅能捕获到携带于传播波中的有限物体信息，而存在于物体表面一个波长范围内的高频倏失波信息被丢失，这就导致了其有限的分辨率。因此，有效利用倏逝波是近场超分辨率成像方法的关键[5]。近场扫描光学显微镜(near field scanning optical microscope, NSOM)是一种常用的技术[6]，它利用能接近物体表面的纳米探针去散射倏逝波，之后由物镜收集以实现高分辨率成像。近场扫描光学显微镜的分辨率仅取决于探针直径，目前其分辨率可低于10 nm[7]。利用负介电常数和磁导率的材料来实现同时收集传播波和倏逝波的超透镜(superlens)是实现超分辨成像和纳米光刻的另一种近场途径[8-9]。利用介质微球增强近场照明同时将倏逝波转化为放大的传播波也是一个有效利用倏逝波实现超分辨率成像的方法[10-11]。但是，由于需激发和收集倏逝波，这些近场超分辨率成像技术在实际应用中面临着操作困难、损伤样品等问题。

远场荧光技术则通过在非线性过程作用下选择性地激活和猝灭荧光载体以突破衍射极限。基于荧光标记的显微镜十分适合研究尺度小于200 nm的生物细胞，能够更加深入了解细胞结构和跟踪细胞内发生的活动。受激辐射损耗(stimulated emission depletion, STED)显微镜利用受激辐射光束激发荧光微粒，同时利用甜甜圈形状的损耗光束抑制微粒周围荧光过程，最终在未损耗区域留下一个突破衍射极限的荧光点[12-13]。记录荧光光点并寻址样品的二维空间位置可实现基于荧光标记的超分辨率成像。另一种广泛采用的超分辨荧光技术是单分子开关和定位显微镜，包括光激活定位显微镜(photoactivated localization microscopy, PALM)[14-16]和随机光学重建显微镜(stochastic optical reconstruction microscopy, STORM)[17-20]。这些方法基于各个荧光团在开和关状态之间的随机光开关。在激发光束的照射下，每一时刻都会有部分荧光团辐射或闪烁，这有利于利用亚像素定位算法对荧光团进行准确定位。通过实现数千次连续周期的随机光开关，可以获得具有极高空间分辨率荧光粒的局域密度。之后通过合并所有单独激活荧光团的位置来重建荧光标记样品的图像。PALM和STORM的典型分辨率可以达到几十纳米[20-21]。除此之外，饱和结构照明显微镜[22]、超分辨率光学波动成像[23]以及基态损耗[24]等其他技术也能够突破衍射极限。所有的远场超分辨率技术都依赖于荧光分子，对样品有选择依赖性。在这些技术中，生物样品的适当标记至关重要。此外，光漂白及由其造成的损伤也是基于荧光标记显微镜中不可避免的问题。

上述讨论的超分辨率技术依赖于临界近场操作或者是样品预处理。近年来，远场无标记超分辨率成像技术在逐步发展[25-34]。基于稀疏性的相干衍射成像技术[28,35-36]可以通过从远场测量的多重空间光谱来重建一些稀疏纳米结构的图像。在测量过程中相位分布和所有倏逝波携带的信息被丢失。利用压缩感知算法重构纳米物体的完整信息，最终得到这些纳米物体的数字图像[28]。在压缩感知算法中，重构操作是一个最小化测量和优化空间光谱之间差别的优化过程。这种技术的局限性在于：当两个稍有不同的深亚波长物体在测量中具有不可分辨的空间光谱时，它将无法分辨。它的应用也局限于仅对稀疏物体的成像[28]。

另一种远场无标记超分辨率技术是将平板衍射透镜集成到共焦扫描显微镜中的纯光学方法。平板衍射透镜的聚焦光斑作为一种光学无损探针在远场照明样品[33-34,37]，其尺寸直接决定了平板衍射透镜型共焦扫描显微镜的空间分辨率。受益于快速发展的纳米技术和强大的优化算法，由微/纳米结构构成的平板衍射透镜可根据实际需求被任意定制，该透镜具有诸多特性，例如超高数值孔径[38]、大聚焦深度[38-39]以及在远场的亚衍射极限聚焦[40-43]，允许超分辨率成像。由于平板衍射透镜在操控焦场方面具有很高的自由度，因此在不久的将来会快速发展，并为各种应用提供特殊的设计。凭借紧凑的尺寸、平整表面、多功能复用以及强大设计自由度，平板衍射透镜是传统物镜、相机镜头等光学元件的一个重要补充或替代品。

本文将重点介绍快速发展的平板衍射透镜的最新进展。首先概括了各种超分辨率成像技术，介绍基于衍射的聚焦光学，并将其作为平板衍射透镜的物理起源，详细讨论平板衍射透镜的焦点、焦深。然后从设计原理、制作工艺、聚焦性能和光学像差等方面讨论了不同平板衍射透镜的结构和性能。根据已有的实验结果，对基于平板衍射透镜的扫描聚焦显微镜和直接宽场成像进行了理论分析，同时详细比较各种光学超分辨显微镜的光学参数。最后本文对平板衍射透镜的研究现状、面临的挑战和未来应用的可能方向进行了简要评述。

1 理论分析

1.1 衍射理论

衍射是水、电磁波以及声波在自由空间和介质中传播的固有现象。它可以用惠更斯-菲涅耳原理解释：新波前是初始波前上大量二次点源发出球面波的相干叠加[4]。基尔霍夫用数学方法将该原理表示成积分，而由麦克斯韦方程组严格推导出的瑞利-索末菲衍射理论对其进行了修正[4]。对一个给定电场U(x0,y0)的单色波，其中x0和y0是空间坐标，其衍射场可以用瑞利-索末菲理论表示：

(1)

(2)

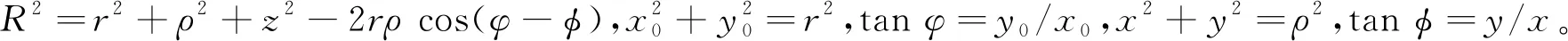
对于相位或振幅被像素化的入射场U，其衍射模式可用式(1)的数值积分计算。假设入射场有(N+1)×(N+1)个像素，每个像素大小为Δx0Δy0,其中Δx0和Δy0分别是x和y方向像素间隔。在有限求和条件下，得到目标平面z上(xi,yi)位置处的强度u(xi,yi,z)：

(3)

式(3)是入射场U和传播因子g的二维卷积，可通过快速傅里叶变化(FFT)进一步简化[4]。如果目标平面光场和入射场有相同的像素大小，即Δxi=Δx0，Δyi=Δy0，且像素数为(M+1)×(M+1)，可以直接得到：

(4)

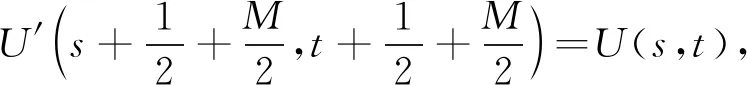
式(2)旨在求解旋转对称透镜(例如波带片型透镜)的衍射。它适用于任何可以在极坐标或柱坐标中描述的衍射问题。需要注意的是，为使用式(2)，U(r,φ)必须用解析式表示。换言之，式(2)具有解析入射场U(r,φ)和像素输出场U(ρ,φ,z)。这意味着式(2)不能描述两个级联旋转对称透镜的衍射，因为第一个透镜的像素输出场不能够作为第二个透镜的入射场。

式(4)可以计算由全息或超构表面调制的像素或离散场的衍射。由于入射光和输出光都是像素化的，式(4)适用于单层或级联的超构表面透镜，以及在多层介质中用于聚焦光的超构表面透镜。当描述光在不同介质中的传播时，可以通过计算介质的折射率来改变式(4)中的参数n。式(4)可以用于模拟超构表面领域的所有衍射问题。

上述衍射理论是基于标量光学，没有考虑光的矢量性质。事实上，矢量瑞利-索末菲衍射具有类似的形式且同样能从麦克斯韦方程组推导出[43]，但包含更多电场分量。研究具有空间变化偏振状态的矢量光束(如圆柱形矢量光束[44-45])的衍射可以参考各种坐标系下的矢量瑞利-索末菲衍射[43]。

1.2 平板衍射透镜设计

传统的物镜利用两介质界面处的折射现象，通过调节其曲率等表面参数，将光聚焦成光斑[46]，如图1(a)所示。从根本上说，衍射透镜利用微/纳米尺度透明圆环的衍射(见图1(b))，采用圆环衍射是由于大多数光学系统中存在旋转对称性。这样的衍射透镜通常由薄膜制成，其厚度(约几百纳米)与透镜的横向尺寸相比可忽略不计[33-34,38,47]。因此，将其命名为具有微/纳结构的平板衍射透镜，以区别于体积大的传统折射物镜，尽管折射物镜在光聚焦时也具有衍射作用。在本文中，涉及的平板衍射透镜主要包括波带片型透镜[33-34,48]、光子筛型透镜[49-53]以及超构表面型透镜[47,54-60]。不同于折射型透镜，这些平板衍射透镜通过优化同心圆环位置来精准调控其所衍射光的干涉来实现聚焦。因此，单环是所有平板衍射透镜中重要的衍射单元，其衍射行为直接决定平板衍射透镜的聚焦性能[61]。

图1(c)中宽度为Δr，中心半径为r0的透明圆环, 其衍射场可以用式(2)进行描述。需要注意的是，当圆环宽度Δr小于一个波长时，透射模式依赖于入射光的偏振态。为简单起见，假设透明环作为具有均匀方位角强度分布的环形光源，这可以通过用非偏振光照射该透明环实现。在这种情况下，圆环透明区域的光在模拟中将被视为一个整体。为获得较好的焦斑，这种环形光源在目标平面的衍射强度曲线应接近于零阶贝塞尔函数，如图1(d)所示。相反，类似图1(e)中聚焦性能差的圆环不应该包含在平板衍射透镜中。

图1 衍射型聚焦理论。(a)折射型透镜聚焦示意图; (b)衍射型平板透镜聚焦示意图; (c)单个透明环衍射单元，环宽Δr，中心半径为r0，目标面z处最大的会聚角为α；(d)宽度较小(Δr=0.5λ)和(e)较大(Δr=3λ)情况下环带的衍射强度分布(点状线)，实线表示第一类零阶贝塞尔函数平方值，z=15λ

目前，平板衍射透镜的设计方法可分为优化方法和无优化方法。已有的优化方法主要有二元粒子群优化算法[33]和遗传算法[50]，它们能很好地解决光学中物理变量的最小化或最大化问题。唯一的无优化方法是通过数值求解一个非线性方程来设计平板衍射透镜，该方程包含平板衍射透镜中所有环的未知环宽和中心半径。在求解该方程之前，必须在预先确定的位置处设置特定的强度分布，以描述预期的焦斑形态。理论上，这些预先定义的点必须是物理上存在的，这样无优化方法才能提供或给出该物理解。牛顿法及其改进算法可用于数值求解该非线性方程。这种无优化算法可有效地设计产生多焦点的二元位相衍射元件，例如光学胶囊[61]、空心瓶光束[62]和亚波长光针[63-65]。

1.3 平板衍射透镜特性

对于平板衍射透镜，其焦斑的横向尺寸可以通过优化其结构(即单个环的宽度和位置)以满足在不同应用中的特殊需求。图2(a)给出了各种焦斑一维(沿x轴)强度分布的详细总结。没有经过优化的传统菲涅耳波带片通常将光聚焦成尺寸约为0.61λ/NA(NA为数值孔径)的爱里斑[5]，与基于球透镜的光学成像系统中定义的瑞利判据一致。除主焦斑外，爱里斑周围存在弱旁瓣，其峰值强度为主焦斑的1.75%[34]，如图2(a)所示。该旁瓣可以被光子筛型透镜[49,53]抑制，但会导致主焦斑尺寸大于瑞利判据，无法应用在纳米成像[34,37]和光刻[66-67]等领域。

尽管旁瓣会增加，突破瑞利判据的亚衍射聚焦在光刻以及超分辨率扫描成像等领域具有巨大应用潜力(见图2(a))。由于空间频率越高的光对应的主焦斑越小，为实现主焦斑尺寸和旁瓣之间的平衡，需要通过调整聚焦所涉及的高、低空间频率的比例来对透镜进行仔细优化和精心设计。极端情况下只包含空间频率最大的光聚焦成焦斑，称为“最大频率点”。此时式(2)中环宽Δr→0，可得到“最大频率点”的电场：

(5)

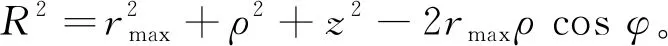
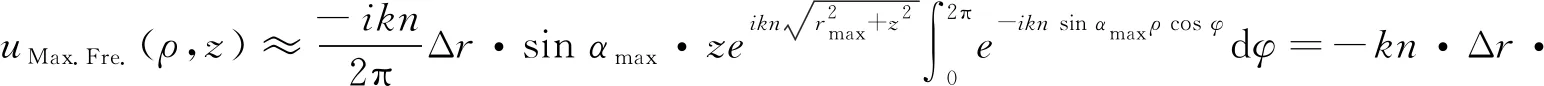
(6)

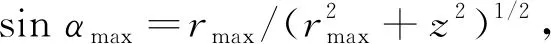
最大频率点的主焦斑(即J0的第一个零点)尺寸为0.38λ/NA，其最强旁瓣和主瓣之间的峰值强度比值为16.2%。由于小的主焦斑尺寸和弱的旁瓣强度之间有很好的平衡关系，因此在实际应用中可以被接受。

此外，可进一步减小主焦斑尺寸使得主焦斑区域处的光振荡速度快于最大频率点。这种现象在数学上称作超振荡[69-73]。相应地，以保持在最大频率焦点的0.38λ/NA作为超振荡判据，即超振荡主焦斑小于0.38λ/NA。根据超振荡理论，主焦斑尺寸原则上可以无限小而不受任何限制。然而，这种超振荡焦斑具有很强的旁瓣，其光学成像的有效视场被限定在旁瓣所包围的有限区域内。在大面积成像中必须解决这一限制。图2(b)描述透镜焦斑大小和数值孔径之间的关系，瑞利和超振荡判据将其分为三个部分[61]。黄色区域表示高于瑞利判据的焦斑的横向尺寸大于0.61λ/NA，青色区域覆盖焦斑尺寸位于两个判据之间亚衍射焦斑，蓝色区域表示超振荡焦斑尺寸低于超振荡判据0.38λ/NA。结合图2(a)，可以发现，在这三个区域中，焦点的旁瓣随着主焦斑横向尺寸的减小而均匀地增大。

图2 平板衍射透镜聚焦。(a)平板衍射透镜不同情况下的焦斑沿x轴强度分布，如瑞利判据之上、亚衍射极限和超振荡点，被瑞利判据和超振荡判据分隔[68];(b)不同数值孔径平板衍射透镜的焦斑尺寸，瑞利判据和超振荡判据将其分成三部分，表示焦斑的特征[68]

透镜还有另一个重要特性：焦深，其直接影响成像和光刻性能。此处讨论的焦深是围绕设计焦平面的纵向范围(或光的传播方向，在此表示为z方向)，在该范围内设计的焦斑可以很好地被扩展，而不会损失光学性能，例如横向光斑大小。在不同的应用中，焦深的需求是不同的，这取决于应用的实际情况。例如，3D光刻[74-75]需要较小的焦深来获得体积抑制点，以提高制造中的轴向分辨率。但是，在扫描共焦显微镜(SCM)[76-78]中则需要更大的焦深，可以照亮具有空间和倾角偏差的样品。对于空气或真空中的传统透镜系统，利用光学不确定性原理[3]，其焦深可以描述为DOF=λ/(1-cosαmax)。最外层光线与光轴之间的最大会聚角αmax与数值孔径为NA=sinαmax系统的最大空间频率有关。对于低数值孔径系统(即小的αmax)，其焦深近似为2λ/sin2(αmax)，被广泛应用于镜头设计[46]。该焦深表达式也适用于标准菲涅耳波带片，其环半径满足[46]：

(7)

式中:f是焦距，n是环带折射率。也同样适用于超构透镜[47,79]，其相位分布为：

(8)

式中:r为径向坐标。

与传统透镜系统的焦深相比，平板衍射透镜通过优化微纳结构来定制焦深参数，使该焦深特性在物理上确实存在。根据焦点的横向尺寸分类，平板衍射透镜的焦深大致可分为两类。首先，对于焦斑大于超振荡判据0.38λ/NA的平板衍射透镜，凭借强大的优化技术，其理论[43,63-64]和实验上[34,38-39,41,80-81]报道的焦深可以达到几十个波长(即使是对高数值孔径平板衍射透镜)。基于相长干涉，这种长焦深可以被视作亚波长光针，它也存在于有相位[63]或振幅[82-84]调制的高数值孔径物镜中。在物理上这种亚波长光针十分奇特，因为它可以传播一段距离而没有明显发散，并且可以在几十个瑞利距离[46](即zR=πw02/λ,其中w0是光针的横向尺寸，通常用来评估激光的发散)范围内保持其良好的形状。例如，实验测量的12λ长针的横向尺寸约为0.407λ[34]，可以传播23个瑞利距离。其工作原理类似于光学空间孤子[85]，后者通常需要复杂的方法，包括非线性超材料[86]、变换光学[87]和各向异性介质[88-89]，以获得无发散的良好匹配光束。这种基于平板衍射透镜的亚波长光针可能为孤子的研究提供一种新的物理视角。

最近，具有略大于超振荡判据(0.38λ/NA)的主焦斑，以及焦深大于2λ/(NA)2的针状焦区的超临界透镜展示了长焦深在光学成像中的重要性[34,37]。和传统物镜、菲涅耳波带片和超振荡透镜不同，这种超临界透镜在亚波长焦斑、弱旁瓣、长焦深和大焦距之间达到了近乎完美的平衡。这种超临界透镜与共焦扫描显微镜相结合，在提高成像分辨率和绘制三维物体方面具有压倒性的优势[34]。

作为平板衍射透镜一种的超振荡透镜，由于在超振荡场中发生相消干涉，其焦深非常有限。这种现象在实验上也被观察证实了[78]，其表明超振荡场中的相消干涉比亚波长光针中的相长干涉需要更严格的光学调控。这意味着严格的相消干涉不能在一个与设计z平面稍有偏离的观察平面上发生，因为它的相位和振幅在多个干涉光束的作用下也会发生变化。目前还没有关于横向尺寸小于0.38λ/NA的自由空间超振荡光针的报道。需要指出的是，虽然一些文献中使用了“超振荡光针”一词，但是那些产生或提出的光针的横向尺寸超过了超振荡判据，并且超振荡点是在光针区域之外获得的。此外，超振荡领域开创者Berry认为包含物体的亚波长细节超振荡场在其传播过程中的焦深在10-45λ量级[90-91]。

对于物镜，其在光学聚焦或成像中的衍射极限是瑞利判据0.61λ/NA(半高全宽(FWHM)为0.51λ/NA)。实际上，只要将物镜和经过优化的衍射光学元件结合起来就可以很容易打破这种衍射极限。因此，瑞利判据并不能精确地预测光的实际衍射极限，特别是对于具有优化结构的平板衍射透镜。以上关于焦点和焦深的讨论表明：新的衍射极限应更新为超振荡判据0.38λ/NA。究其原因为：首先，当焦斑小于0.38λ/NA时，其旁瓣变强，甚至可以超过主瓣。这种旁瓣在成像会导致极其有限的视野，这也是纳米光刻中的一大障碍。其次，超振荡点的短焦深(<λ)使得在实际应用中光学对准极具挑战性，导致对样品空间偏差和倾角的容忍度较差。最后，当超振荡透镜中的主焦点尺寸为深亚波长时，其强度很弱，与旁瓣相比，可以将其视为噪声。

2 平板衍射透镜

为了区分不同类型的平板衍射透镜，根据它们的微纳结构特征将它们分为波带片型透镜、光子筛型透镜以及超构表面型透镜。

2.1 菲涅耳波带片型透镜

标准菲涅耳波带片作为一种波带片型透镜，已经在许多领域被研究和使用。因此在这里只介绍由环带被优化过的波带片型透镜的最新进展。这些透镜相较于传统菲涅耳波带片展现出卓越的性能，例如焦点、宽谱操作。根据调控类型的不同可将其分为振幅和相位波带片型透镜两大类。

振幅波带片型透镜通常在金属薄膜(例如金、银、铬等)上刻蚀环带而成，其制造过程十分简单。由25个透明环带组成的超振荡透镜(最小环带宽200 nm，最大环带宽1 200 nm)在油浸环境下拥有尺寸(半高全宽)为0.29λ的焦斑以及16.1λ长的焦距[33]。该高数值孔径超振荡透镜激发了对不同波带片型透镜的深入研究。类似的二元振幅超振荡透镜在圆偏振光入射下可以产生圆偏振亚衍射极限光针[39]。之后，直径为978.4 μm的微米结构透镜可将带有涡旋位相的角向偏振光聚焦成12λ长的亚波长光针，其焦距可达到240λ(λ=633 nm)[38]。由于其微米量级的结构尺寸，可采用激光直写或者标准紫外光刻进行批量生产，无需高成本和费时的电子束或聚焦离子束刻蚀。作为超临界透镜的第一个原型，数值孔径高达0.98的微米尺度透镜在紫外光入射下可以产生接近超临界判据0.38λ/NA的焦斑以及长焦深[34]。该透镜在非侵入式成像领域具有极大优势。原则上，不同波长的入射光(如红光、绿光以及蓝光)会产生具有轻微纵向偏差的光针，称为色散。但是，这些不同颜色光针的纵向延伸使其在某个区域上会部分重叠，在重叠区域里不同波长的焦斑可以在同一横截面上获得[80]。此外，由三个纵向堆叠的菲涅耳波带片组成的低数值孔径三维透镜，它们在三原色上具有相同的焦距，以校正色差[92]。尽管这些振幅透镜具有优异的性能，但它们的总效率限制在10%以内。近年来，二维材料(例如石墨烯和过渡金属二卤化物(TMDCs))凭借其强的光和物质相互作用以及高折射率开始被应用于纳米光电器件领域。实现高效率(>32%)、超宽带(400～1 500 nm)三维亚波长聚焦的超薄透镜通过激光直写技术在200 nm厚氧化石墨烯薄膜上制成[93]。尽管该透镜可以同时实现振幅和相位调制，但相位调制对聚焦的贡献十分微弱。这种透镜在经过扭曲[93]或暴露在太空、化学和生物恶劣环境之后仍然具有出色的光学性能[94]。但是其波长量级的厚度并没有充分利用二维材料的超薄特性，且减小氧化石墨烯厚度会影响聚焦效率和分辨率。之后由单层TMDC(WSe2)制作而成的超薄衍射透镜可以实现在远场三维亚波长聚焦和衍射极限成像[95]。该透镜WSe2薄膜厚度仅有0.7 nm，经过激光直写的区域厚度也只有20 nm左右。但这些二维材料平板衍射透镜的主焦斑尺寸均未突破瑞利判据。最近，利用多层TMDCs激子共振造成的强吸收，厚10 nm的MoS2超临界透镜具有0.44λ的主焦斑以及20 μm的焦距，结合扫描共焦显微镜可实现高质量超分辨率成像[37]。

理论上提高效率约40%[96]的二元相位透镜被用于调制径向偏振光[97]和圆偏振光[98]。与振幅透镜不同的是，这些在透明电介质(如SiO2、Si3N4)上制作的相位透镜具有尺寸变化的凹槽，从而引入相长干涉所需的π相位差。通过传统物镜或高数值孔径平板衍射透镜聚焦，径向偏振光在聚焦区域有一个横向尺寸为亚波长的强纵向偏振光针[65]。使用基于纳米光纤光栅近场扫描光学显微镜测量的纵向偏振光针是自2008年理论预测[63,65]以来第一个实验证据[97]。最近，基于单层TMDCs(MoS2)的超临界透镜利用损失辅助奇异相位[99]实现π的相位调制，在距离透镜45 μm远场区域得到亚衍射极限的焦斑[100]。当使用双层MoS2时还可以实现435～585 nm连续波段内的亚衍射极限聚焦。不同于利用超薄二维材料实现振幅调制[37,95]，该二元相位透镜打破了为获得π或2π相位调制需要波长量级厚度薄膜的限制，可以在接近材料的物理厚度极限下(0.667 nm)实现相位调制。和上述透射型波带片型透镜不同，该透镜基于反射模式，且其效率非常低，限制了其实际应用。

2.2 光子筛型透镜

光子筛是在不透明金属膜上的穿孔结构[53]。它们最初被设计用来抑制旁瓣。最近，人们发现纳米尺度的圆孔没有存在于纯亚波长宽度波带片透镜中的偏振依赖效应[50,52]，它区别于由波长量级圆环组成的超振荡透镜[33]。一种分形光子纳米筛透镜，其纳米孔位于菲涅耳波带片环带区内，用于抑制旁瓣和高阶衍射[51]。由于较低的数值孔径，该透镜的焦斑尺寸并不突出。为了获得更小的焦斑，最外环需要更多的纳米孔以包括空间频率更高的光，这会导致透镜的整体尺寸变大，从而给模拟和设计带来更多挑战。当孔的尺寸在纳米量级时，需要用严格的矢量衍射理论来近似透镜衍射场。对于大尺寸的光子筛透镜，由于计算量大，常用的有限差分时域法模拟方法将难以适用。

为了解决这一问题，利用混合方法来解析描述光从纳米孔衍射的矢量场，为在纳米尺度上高精度地操纵光提供了依据[50]。基于此，一种位置经过优化的光子筛，通过精确控制衍射光在焦平面上的干涉，实现了高数值孔径聚焦透镜，其深亚波长聚焦光斑超过了线偏振光的超振荡判据[50]。此外，波前编码光子筛可以实现宽谱操作[49]。纳米筛平台在可见光和红外波段的透过率较低，导致基于纳米筛光学器件的效率较低。然而，由于对短波长光源具有更高的透射效率，使得纳米筛平台能够在短波长下对透射波进行精确操纵，例如在新型显微镜中的X射线[101]和物质波[102-103]。

2.3 超构表面型透镜

超构表面是一种空间变化的超薄纳米结构，可以实现对光的相位、振幅、波长和偏振等的完全控制。作为超构表面最重要的应用之一，超构透镜与商用物镜相比具有超薄、易集成等特点，在光学聚焦和纳米成像方面的应用受到了广泛关注。Capasso小组的综述文章全面介绍了可见光波段内基于TiO2(氧化钛)超构透镜的光学性能[104]。此外，Lalanne和Chavel还从衍射光学元件的历史观点详细讨论了超构透镜的潜在局限性[105]。本文将着重讨论超构透镜光学像差和宽带操作等基本挑战。

不同于二元相位或振幅调制的波带片型透镜和光子筛型透镜，超构透镜可以通过渐次改变纳米结构体的形状(梯度相位)或旋转尺寸固定纳米结构体的方向(几何相位)获得多级相位。最初的超构透镜具有很低的数值孔径，可以在可见光和红外波段使用，其通过使用V型等离子纳米结构实现梯度相位[60,106]。但是，在这种透射模式下，这些超构透镜只能将一小部分入射偏振光转换成具有交叉偏振和所需相位的透射光，效率较低。

目前，由低吸收电介质纳米结构(TiO2用于可见光波长[47,104]和Si用于近红外波长[107-109])制成的超构透镜被认为是在透射模式中实现高效率聚焦的最佳候选者。例如，在915 nm和1 550 nm的近红外波长下，由非晶硅纳米结构制成的超构透镜可实现约80%的聚焦效率[107-109]。具有几何相位的TiO2超构透镜在405 nm到633 nm的可见光波长范围内也被证实具有66%～86%的高效率[47,104]，并且在手性成像和油浸纳米成像领域也有卓越表现。电介质超构表面利用了纳米结构中存在的磁共振，这意味着对于高效率的超构透镜，介电材料中折射率的虚部必须很小。单晶硅在可见光和近红外波段具有低吸收的特性，也可以用来制作超构透镜，效率可以达到71%。为实现高效率反射式超构透镜，可以在均匀金属和绝缘体膜上制作纳米结构超构表面。

3 平板衍射透镜像差分析

在基于平板衍射透镜的光学系统中，光学像差主要来自于离轴物体和多波长照明。但是传统物镜还存在轴上像差，即球差。由于球面透镜的缺陷，光轴上同一点光源发出的光线经过透镜后不能聚焦在同一位置。平板衍射透镜在经过设计和优化后可将入射到透镜边缘和中心的光聚焦在同一位置，因此在单波长平板衍射透镜中不存在球差。

3.1 离轴像差

通过使用单个平板衍射透镜进行光学成像，可将物体P成像在设计的像面上，物距和像距分别用l1和l2标记，如图3(a)所示。平板衍射透镜的结构需要经过合理设计以保证相长干涉，即轴上同一物体所发出的光经过透镜后到达设计的像面位置需要经历相同的光程。在这种情况下，成像型菲涅耳波带片的半径需要满足：

(9)

相似地，超构透镜的相位分布需要修改为：

(10)

需要注意的是，式(9)和(10)只对轴上物体成立，对于离轴物点仍然存在像差。

为说明在成像平板衍射透镜中的离轴像差，本文假设物体P位于(ξ,η)，因为任何离轴物体都是由无限个点组成。平板衍射透镜的离轴像差可以用离轴点源P发出到理想像点Q的中心和边缘光线之间的光程差来评估。在经过简单数学推导后，光程差可以表示为：

(11)

式中：l1和l2分别是物距和像距，R是平板衍射透镜的半径，θ是光轴和中心光线之间的夹角。式(11)可以描述任何类似平板衍射透镜的离轴像差。

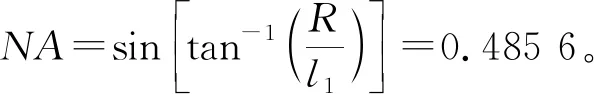
图3 平板衍射透镜离轴像差。(a)成像平板衍射透镜光路图，物距和像距分别为l1和l2,平板衍射透镜的结构(或相位)可由式(9)(或式(10))推出，点源P(ξ,η)位于物平面用来研究平板衍射透镜的像差；对于半径为100λ的超构透镜，其在低数值孔径(l1=180λ,l2=360λ)和高数值孔径(l1=60λ,l2=80λ)下像平面聚焦强度在(b)和(c)显示；(d)斜入射下菲涅耳波带片的像差，在0°,1°,2°倾斜角度下焦平面的光强分布

除了图3(a)所示的离轴情况之外，在平面波照明下，传统菲涅耳波带片和超构透镜分别满足式(7)和(8)描述的结构和相位分布，通过设置l1→∞将式(11)简化为：

(12)

式(12)已被用于具有低数值孔径菲涅耳波带片光学像差的研究[111]。在倾斜角度为1°和2.5°入射光照射下的超构透镜的离轴像差已经从理论和实验两方面被研究[107]。为了比较超构透镜与菲涅耳波带片的离轴像差，模拟了在倾斜光照下菲涅耳波带片的焦面光强分布，其光路图如图3(d)左侧所示，右侧展示了θ=0°、1°和2°的焦平面光强分布。结果表明，菲涅耳波带片和超构透镜具有相似的离轴像差。

在低数值孔径系统中已经有不同的方法被用来校正离轴像差以实现宽视场成像或聚焦，如表1所示。由校正超构透镜和聚焦超构透镜组成的双面超构表面被提出以校正850 nm波长下的离轴像差，在30°倾斜入射下仍然具有良好的聚焦光斑[107]。虽然这种级联超构透镜存在着效率低下、集成度差、超构透镜对准困难以及较低成像分辨率等问题，但是它证实了利用多个超构透镜校正离轴像差的可行性。相似的两个超构透镜级联系统可以校正532 nm(中心波长)波长下的离轴像差，最大入射光倾角可以达到25°[112]。在这种级联系统中，第一个透镜通常还作为孔径光阑以缓解严重的离轴像差。这意味着如果第一个校正透镜和第二个聚焦透镜的尺寸一样大，离轴像差不会被校正。之后，同样在850 nm工作波长下的单个惠更斯纳米天线型超构透镜在前置孔径光阑辅助下可实现±15°视场下的高质量成像[113]，但是其效率较低。同样利用单个惠更斯纳米天线型超构透镜可以实现在中远红外波段下近90°离轴像差的校正[114]，同样也需要前置孔径光阑。上述宽角度超构透镜的焦斑尺寸都没有突破衍射极限，一个数值孔径高达0.97的电介质超构透镜可以实现超分辨率聚焦，焦斑尺寸只有阿贝衍射极限的87.4%，但是视场仅有4°。目前可实现远场超分辨率聚焦的超振荡透镜或超临界透镜被限制在正入射情况下工作，这意味着基于此的远场超分辨共焦显微镜仅能通过逐点扫描，在二维区域内以几纳米的空间步长移动样品来获得超分辨率图像，成像速率相对较慢。由于该超构透镜提供了一定入射角范围并可以实现超分辨率聚焦，因此可进行光束扫描从而实现快速成像[54]。

表1 校正离轴像差超构透镜

3.2 色 差

色散是光学材料的重要特性之一，在光学元件和系统的设计中起着至关重要的作用。传统折射光学依赖于传播过程中的相位积累。具有正常色散玻璃材料的折射率随波长的增大而减小，导致红光经传统透镜聚焦后具有更大的焦距，如图4(a)所示。另一方面，通过借助于振幅或相位掩模透射光的干涉来操作，衍射光学元件表现出相反的色差。长波长对应着短焦距以及大折射角，如图4(b)所示。为详细说明平板衍射透镜的色散，展示了数值孔径为0.7的超构透镜在红光(633 nm)、绿光(532 nm)以及蓝光(450 nm)照射下的焦斑，如图4(c)所示。根据式(8)在绿光下设计超构透镜被直接用于对红光和蓝光聚焦，由图4(c)三色的焦斑沿光轴分散分布且红光的焦斑更靠近超构透镜。

图4 传统折射光学元件(a)和衍射光学元件(b)中的色散;(c)450 nm、532 nm和633 nm波长照明下超构透镜焦区光场分布，数值孔径为0.7超构透镜的设计焦距为25 μm，设计波长为532 nm，相位公式如式(8)所示；(d)数值孔径为0.2～0.9的超构透镜的色散图，横向坐标表示沿z传播轴的轴上强度分布，设计波长532 nm处的焦距固定在25 μm，通过改变超构透镜半径获得不同的数值孔径，红色、绿色和蓝色分别表示波长633 nm、532 nm和450 nm处的强度，白线表示的光强分布和(c)中一致

对于衍射光学元件而言，色差主要来源于材料、共振以及传播色散[115]。材料色散[116]，指的是材料的折射率和入射光波长有关，存在于大部分的衍射光学元件。共振色散，发生在光子筛透镜以及超构透镜当中，指通过光波模式与纳米结构相互作用获得的调制振幅或相位与波长、结构几何和材料折射率有关。材料色散和共振色散通常统称为调制色散，因为材料色散是在光模的共振过程中考虑的。传播色散是指多波长光的相位或振幅即使在传播了相同距离后也具有与波长相关的值，这在所有光学系统中都会发生，原则上不能消除。

将多个单色元件在空间上重组为一个消色差器件为解决色散问题提供了一种途径。分别在红光(650 nm)、绿光(550 nm)以及蓝光(450 nm)波长下工作的三个超薄菲涅耳波带片沿光的传播方向被纵向堆叠以实现在同一焦平面上同时聚焦三种光[92]。三个菲涅耳波带片各自嵌有不同材料制作的纳米圆盘(铝调制蓝光，银调制绿光，金调制红光)可以支持各自波长下的局域表面等离子振荡。这种创造性的多层设计实现了第一个彩色校正的超构表面三重透镜，但由于金属损耗和制造技术限制，较低的聚焦传输效率(5.8%～8.7%)限制了其应用。将在三个波长下工作的超构透镜进行横向空间复用也可校正多波长色差[117]。该复合超构透镜由三个超构透镜互补交错而成，分别可将红光(480 nm)、绿光(550 nm)以及蓝光(620 nm)聚焦到同一焦面。Faraon等利用两种横向空间复用方式(基于大规模分割和单个衍射单元交织)设计的复合超构透镜消除了915 nm和1 550 nm波长的色差[118]。虽然基于大规模分割设计的复合超构透镜两个波长的聚焦效率更接近，但是会导致焦点变形，而基于基本衍射单元交织的超构透镜不会出现这种问题。不同于以上利用空间复用方法消除多波长色散的方式，Capasso等提出了利用色散补偿方法来抑制色散[119]。通过对微纳结构的合理设计使得总色散(即调制色散和传播色散之和)为零。基于色散补偿设计的超构透镜和超构表面偏折器可以将1 300 nm、1 550 nm和1 800 nm的近红外光分别聚焦到同一平面和偏折同样角度，但是它们仅在设计波长下表现良好。传播色散取决于器件与目标平面之间的距离，根据实际情况的不同，器件的性能也会发生改变(例如菲涅耳区或夫琅禾费区)。另外，只有当调制色散的调谐范围足够大且能补偿传播色散时，该方法才有效。

相较于消除多波长色散，对于利用平板衍射透镜实现连续宽波段色差校正的实际需求更加迫切。通过改进二乘法优化得到的柱面透镜可以在可见光(450～600 nm)波段内抑制色差[120]。但由于低效率和低数值孔径，以及较差的聚焦效果都限制其广泛应用。Wang等利用新的设计原理实现了宽波段消色差超构透镜，可以消除1 200～1 680 nm近红外波段内的色差[121]。传统描述超构透镜相位分布(见式(8))被分成基本相位和像差校正相位，前者可以通过超构透镜微纳结构的几何相位获得，后者可以通过单个微纳结构的相位响应获得。这两种相位在机理上完全不同，不会相互影响，可以通过简单的叠加同时获得。他们利用由一对特殊的金纳米棒、SiO2间隔棒和金制反射器组成的三明治结构作为基本衍射单元，以实现工作波长的线性相位补偿。之后，由于较高的等离子体频率和较低的可见光损耗，铝被用于工作在400～667 nm的无色差超构透镜的类似设计中，效率高于20%[122]。

反射式超构透镜证明了在近红外波段为消除宽谱色差将相位分成基本相位和消色差相位的有效性。尽管反射型超构透镜在某些情况下十分有用，但是透射型光学元件在实际应用中仍然有很高的需求，尤其是工作于可见光波段内的超构透镜。Wang等使用GaN实现了400～660 nm可见光波段内消色差的透射型超构透镜[57]。在可见光范围内，GaN具有低损耗以及高折射率等特性，同时具有较高的硬度和理化稳定性以及低成本和半导体铸造兼容性，是超构透镜材料的理想选择。由于高折射率介质纳米结构之间的弱光耦合，以及波导型腔的多谐振，可以直接通过增加纳米结构的厚度来获得较大的相位补偿。在相同的设计原理下，在3.7～4.5 μm连续红外波段工作的圆偏振入射超构透镜可以有效消除色差[123]。

另外，Capasso等利用相互靠近两个TiO2纳米柱作为耦合波导实现了在可见光波段内透过型消色差超构透镜，其数值孔径为0.2[58]。超构透镜相位(见式(8))在设计中心频率处被拓展成泰勒级数。要实现在设计中心频率处具有一定带宽的消色差聚焦不仅需要满足基本相位，还要同时满足高阶相位(群时延以及群时延色散)。传统的衍射透镜仅能满足需要的基本相位，即在设计频率处的相位分布。对高阶相位的忽略就会导致色散。基本相位分布会形成球面波前，群时延项补充了不同波包到达焦点的时间差，更高阶相位(包括群时延色散项)确保了所有的波包相同。其净效应是使波包在焦点处到达时间的传播最小化，以确保它们相干相长。通过同时控制相位、群时延以及群时延色散最终实现了几乎覆盖可见光波段内(470～670 nm)的色差校正。这代表了超构透镜在消除连续宽波段色差技术水平的一个重大进步。

在以往的宽波段消色差超构透镜的研究中，受设计原则的限制，几乎所有的超构透镜都只在圆偏振光下工作。然而，偏振不敏感的超构表面更适合于实际应用。最近，Shrestha等[124]在近红外波段展示了一种偏振无关的宽波段消色差超构透镜，其工作波长为1 200～1 650 nm，与互补金属氧化物半导体(CMOS)兼容。通过选择合适的几何形状和参数，在选定的带宽范围内满足相位和相位色散，通过偏振无关的消色差超构透镜实现了1 200～1 650 nm的近红外波段的恒定焦距和50%的聚焦效率，在缩小成像系统中具有广泛的应用。但由于使用对称的纳米结构来实现偏振无关性，失去了一定的设计自由度，这限制了超构表面器件的相位调整能力。和空间复用以及对称性相关的设计方法不同，基于各向异性的TiO2纳米结构的宽带消色差偏振不敏感超构透镜可以在460～700 nm的可见光范围工作，同时保持接近衍射极限的焦斑尺寸，其数值孔径为0.2[56]。

尽管可见光以及近红外连续宽波段的色差已经可以被校正，但是校正高数值孔径透镜的色差仍然具有挑战性。为了进一步说明，本文展示了一个超构透镜的详细焦移(其参数与图4(c)中的参数相同)随着超构透镜数值孔径的增加而增大，如图4(d)所示。可以发现当数值孔径小于0.8时，焦斑可以保持良好形态。但是在非设计波长处，当数值孔径高于0.8时会出现球面像差(见图4(d)中的红光和蓝光)，表明在红光和蓝光波长处的焦点区域中产生了纵向延伸的针状光场。这意味着在高数值孔径透镜中同时存在色差和球面像差，这已在数值孔径高达0.98的SiN超构透镜中被实验观察到。由于两种像差(球差和色差)的存在，可以预测在没有像差校正的情况下，数值孔径大于0.8的超构透镜(相位函数服从式(8))只能在设计波长下有效工作。

4 平板衍射透镜应用

平板衍射透镜可以实现强聚焦，也可以直接应用于光学成像、光刻以及光电子能谱仪。本节将讨论平板衍射透镜的应用。

4.1 成 像

大部分强聚焦波带片型以及光子筛型透镜可以将入射光聚焦成所设计的焦斑，但是由于存在严重的像差不能直接用于成像。为实现成像，这样的平板衍射透镜可以集成在扫描共焦显微镜中作为照明光源，因此称为扫描成像。传统的菲涅耳波带片(式(7)或式(9))和超构透镜(式(8)和式(10))可以对一些物体直接成像。下面将具体介绍这两种成像方式。

4.1.1 扫描成像

首先将介绍基于平板衍射透镜扫描共焦显微镜的成像理论。如图5(a)所示描述了基于平板衍射透镜扫描共焦显微镜的光学系统。平板衍射透镜作为聚焦透镜在物镜的物平面产生形态良好的焦斑。这个焦斑作为光源照明放置在平板衍射透镜和物镜共焦平面处的纳米物体上。具有放大倍数M的物镜用于收集纳米物体的散射光。半径为R的小孔被放置在物镜的像平面。理论上探测器应该紧贴小孔放置，因为探测器仅仅是用来探测被纳米物体散射的光子数以作为扫描成像的像素值。在这个光学系统中，平板衍射透镜和物镜需要很好的对准，物体在三维平移台的帮助下只能在具有横向坐标(x0，y0)的共焦平面上移动。当物体在共焦面上扫描时，探测器记录物镜对物体的每个扫描位置所采集的强度。通过对目标扫描位置与检测信号相关联，可以借助计算机处理软件对目标图像进行重建。假设平板衍射透镜在物体平面产生的电场为h1(x0,y0),物体在物平面的复振幅是t0(x0,y0),收集物镜的脉冲函数是h2(xi,yi;x0,y0),可以推导出在xi-yi像平面的复振幅为:

(13)

式中：xs和ys是物体在共焦面上被扫描时相对于原点的横向偏移量，在式(13)中物镜像平面的电场依赖于共焦面上物体的偏移量。孔径允许选择像平面上的部分强度作为探测信号。假设孔径的光瞳函数是P(xi,yi),可以获得物体的重建图像：

(14)

式(14)是基于平板衍射透镜扫描共焦显微镜的最终重构图像。对于物镜来说(有效直径为D),其脉冲响应h2(xi,yi;x0,y0)近似为：

(15)

式中：d0和di是物距和像距，λ是操作波长，J1(t)是第一类一阶贝塞尔函数，参数t为：

(16)

式中：NA和M分别是数值孔径和收集物镜的放大倍数，波长k=2π/λ。为评估平板衍射透镜型扫描共焦显微镜的成像分辨率，采用点扩展函数(PSF)，将目标设为一个极小点，其振幅函数为t0(x0，y0)=δ(x0，y0)。这种情况下，式(14)简化为：

(17)

式中，符号“⊗”代表符号前后两项的卷积。式(17)产生了平板衍射透镜扫描共焦显微镜的点扩散函数。点扩散函数的半高全宽可以评估成像分辨率。

本文讨论基于平板衍射透镜扫描共焦显微镜的一些成像结果。图5(b)展示了纳米孔物体及其在油浸超振荡透镜扫描共焦显微镜下扫描图像，它可以在油中分辨出两个直径为210 nm、间隙约为λ的孔(λ=640 nm)[33]。尽管旁瓣在标准显微镜映射后已被物镜抑制，但超振荡焦斑中的高旁瓣导致最终图像中的高背景。在超振荡透镜的所有光学特性中，旁瓣可能是获得高质量成像的最大挑战，因此被视为超振荡技术的限制因素之一。

为了避免超振荡透镜的这些缺点，Huang等提出并设计一种超临界透镜，它可以在λ=405 nm下产生一个横向尺寸为0.407λ的12λ长针状焦场[34]。这种超临界透镜集成扫描共焦显微镜，具有图5(c)所示的点目标成像结果。它可以分辨两个直径为165 nm，间隙为65 nm孔。实验得到了清晰且无背景的图像，验证了所提出的基于平板衍射透镜扫描共焦显微镜理论的有效性。如图5(c)所示，由许多纳米级宽度透明曲线组成的复杂“狮头”也可以高质量成像。由于超临界焦斑提高了成像分辨率，这种基于超临界透镜扫描共焦显微镜在成像质量方面优于传统扫描共焦显微镜和透射显微镜。此外，超临界透镜中产生的光学针为显微镜界开启了一个新领域，可以绘制三维物体的横向细节，如图5(d)所示。即使物体位于离焦平面也能实现高分辨率成像，而其他显微镜不具备该功能。

除了菲涅耳波带片型平板衍射透镜，超构透镜也实现了高质量扫描成像。Chen等首次展示了数值孔径高达1.1的液浸平板超构透镜[59]，其多功能性适合任何液体并且能够提供衍射极限大小的焦斑，聚焦效率约为50%。通过将超构透镜集成在商用扫描共焦显微镜，在波长λ=532 nm处实现了空间分辨率约为400 nm的衍射极限成像。同时也实现了最小线宽为256 nm、整体尺寸60 μm×60 μm大范围无光学像差扫描成像，如图5(e)所示。限于该超构透镜衍射极限大小的焦斑尺寸，其扫描成像的空间分辨率并不是特别出色。

最近，Wang等提出了基于多层二维材料MoS2的超临界透镜，其厚度仅有10 nm，在450 nm入射光照射下可以在离透镜20 μm处产生横向尺寸为0.44λ(198 nm)的焦斑，其焦深为5λ(2 μm)[37]。将该超临界透镜集成到扫描共焦显微镜可以分辨中心距为200 nm的两条狭缝，同样在450 nm波长下工作的宽场显微镜以及传统扫描显微镜(物镜数值孔径均为0.9)均不能分辨。同时还实现了线宽为50 nm、整体尺寸为10 μm×10 μm大范围“祥云图腾”高质量扫描成像，没有慧差以及扭曲等光学像差，如图5(f)所示。相较于其他扫描共焦显微镜，该平板衍射透镜透镜型扫描共焦显微镜具有卓越的性能，如，超薄的厚度、更高的分辨率(见表2)，能实现具有目前最小特征尺寸图案的高质量扫描成像(即祥云图案的线宽50 nm)。当使用具有更大数值孔径的液浸物镜时会进一步提高其分辨率。数值模拟同时证明用非相干光照明会进一步提高其成像质量，但是会降低焦斑质量。这种基于二维材料的超临界透镜扫描共焦显微镜对下一代扫描共焦显微镜的发展具有很大的影响。

表2 平板衍射透镜型共焦扫描显微镜

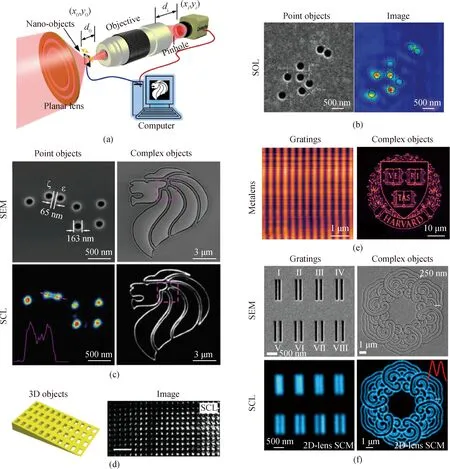
图5 平板衍射透镜型扫描共焦显微镜。(a)工作原理[68]；(b)超振荡透镜扫描共焦显微镜对随机点物(左)的成像结果(右)[33]；(c)超临界透镜扫描共焦显微镜对点物以及复杂物体(第一行)的扫描成像结果(第二行)[34]；(d)超临界透镜扫描共焦显微镜对三维物体(左)的成像结果(右)[34]；(e)超构透镜扫描共焦显微镜对光栅(左)以及复杂图案(右)的扫描成像结果[59]；(f)二维材料超临界透镜扫描共焦显微镜对光栅和复杂物体(第一行)的成像结果(第二行)[37]

4.1.2 直接宽视场成像

尽管存在严重的像差，超构透镜(满足式(8)和(10))和菲涅耳波带片透镜(满足式(7)和(9))可以直接对物体进行成像。下面将主要讨论超构透镜的成像以及像差。

图6 平板衍射透镜直接成像。(a)成像平板衍射透镜示意图，物距和像距分别为l1和l2;(b)成像超构透镜的成像结果(相位满足式(10)),半径R=80λ,l2=1.2l1，黑色图是由透明圆孔阵列组成的物体，彩色图是物距从100λ到800λ相应的成像结果；(c)低数值孔径超构透镜手性成像[125]；(d)高数值孔径超构透镜成像[107];(e～f)慧差校正级联超构透镜成像[47]

对于成像分辨率，数值孔径为0.8的超构透镜能够分辨两个孔之间的450 nm间隙[47]。考虑到其焦斑的半高全宽为375 nm，该超构透镜的成像分辨率显著降低。从根本上讲超构透镜中的电介质纳米结构对于具有大倾斜角的入射光具有较低的透射率，这对应着从物体发射的大发散角射线(即高空间频率)。在超构透镜的图像信息处理过程中，高空间频率光的缺失以及减弱会导致物体细节的丢失，最终导致成像分辨率的降低。因此，受限于大入射角下电介质纳米结构的低透过率，用作直接成像的超构透镜很难达到超越瑞利判据的分辨率。相比之下，扫描模式下工作的超构透镜在532 nm波长下可以获得200 nm的分辨率[59]，如图4(e)所示。尽管扫描方式的速度比直接成像方式慢，但其成像分辨率高、像差小、目标成像大等优点，使得扫描模式在许多应用中更加实用。

4.2 光 刻

亚衍射聚焦在需要小的主焦斑尺寸以及弱的旁瓣的纳米光刻中有着重要的应用。超振荡焦斑由于强旁瓣的存在并不适用于光刻。波带片型以及光子筛型透镜已经应用于X射线、极紫外以及可见光波段内的光刻。例如，在405 nm波长下工作的数值孔径高达0.9的光子筛型透镜可以制造400 nm周期的光栅[66]。光子筛和波带片透镜中包含的结构基于式(7)中定义的标准参数，从而导致衍射极限聚焦点和所制造的结构在波长范围内。最近，厘米级超临界透镜阵列在633 nm入射光照射下可以在远场得到均匀的亚衍射极限(横向尺寸仅有爱里斑0.75倍)焦斑阵列[126]。得益于透镜结构的非亚波长特征尺寸，这种厘米级透镜阵列可以通过无掩模紫外光刻技术在10 min内制造完成。这代表了平面衍射透镜发展的重要进步。具有亚衍射极限聚焦能力的平板透镜阵列提供了在高精度纳米加工领域中的潜在应用。

4.3 光电子能谱仪

角分辨光电子能谱仪利用X射线或真空紫外(VUV)光照射样品以测量光发射电子的能量和动量来表征量子二维材料的电子结构[48]。目前7 eV真空紫外型光电子能谱仪具有较差的分辨率，高数值孔径折射透镜具有严重的球差，另外由于对真空紫外具有强吸收,仅有非常有限的材料可以校正像差，此外由于真空紫外光不可见且所有光学元件需要放在真空室内，导致测量入射光的质量(准直、均匀度以及有效直径)以及对齐光学元件都非常困难。为克服这些困难，Mao等[48]设计了一种177 nm真空紫外激光扫描光电子显微镜光源，采用焦斑约为0.76 μm无球差菲涅耳波带片。长达45 mm的透镜工作距离允许该系统可以作为一个具有离轴反射和透射的真空紫外荧光光谱系统。与传统荧光光谱仪相比，该系统不需要感光剂掺杂，极大地促进了样品的制备，并扩展了其表征未勘探材料的能力。所提出的真空紫外激光系统可以重新装备，用于低成本的角分辨光电子能谱仪，推动量子材料、凝聚态物理和纳米光子学的发展。

5 结语与展望

在过去的十年中，通过研究衍射型聚焦光学器件、新光衍射极限、超振荡现象、光学仿真中的光学优化技术，利用优化的微/纳米结构实现了远场、亚衍射极限聚焦，开发了新型光学材料，例如超材料、超表面、光子筛和波带片。这种体积小、重量轻、平面度高、光学性能优越的平板衍射透镜对传统物镜提出了挑战。它们在重塑当前的显微镜和成像行业，在满足便携式设备、信息技术和自动化对微型光学元件的需求上具有巨大的潜力。然而，在其最终的工业应用之前，还需要克服一些挑战。

首先，平板衍射透镜在聚焦和成像方面的光学效率受到限制。二元调制的波带片和光子筛型透镜理论上效率低于40%。尽管电介质超构透镜将效率提升至80%～90%，高频光的低透过率降低了高数值孔径超构透镜的成像分辨率。即使在聚焦时，入射在高数值孔径超构透镜外层的光对于焦斑几乎没有贡献，因为超构透镜中的大像素间距导致入射光到焦点的衍射效率较低。再者，在平板衍射透镜两种成像模式下，与高质量成像相关的问题仍然存在。例如，用于宽场成像模式的超构透镜的光学像差在纳米成像等高级应用中需要被校正。平板衍射透镜型扫描共焦显微镜的成像速度需要被进一步提升以获得具有精细结构的大尺度图像。此外，在可见光和紫外光谱等短波波段，缺乏高折射率和低吸收的介电材料来实现高效率的超表面。另外，需要解决平板衍射透镜微纳结构在实际应用中的稳健性问题。最后，需要建立大批量生产具有密集微纳结构的大面积平板衍射透镜工艺。实现可重新布控或可编程的平板光学透镜和器件在动态成像和显示中的应用是未来的一个巨大的需求和挑战，尽管已经通过使用相变材料证明了一些初步的活性纳米器件、栅极可调谐导电氧化物、电控等离子体或可拉伸衬底。

为应对上述挑战，未来的工作可能集中在基础物理研究和技术解决方案两个方面。解释光针横向尺寸不能低于0.38λ/NA的基本物理需要更多的数学证明，其背后可能会存在一些新的物理现象。在没有明显旁瓣的情况下，“光学远场聚焦的极限是什么”仍然是一个悬而未决的问题，就如同瑞利判据被更新为超振荡判据0.38λ/NA。二维材料在平板衍射透镜领域的成功应用为设计多功能且性能优异的平板衍射透镜提供了新的方向。对比传统物镜，基于多个或级联超构表面的单透镜可能为校正或减少光学像差提供一种可行的方法，以满足成像和加工的实际要求。利用基于超临界透镜的扫描共焦显微镜对三维物体的水平细节进行成像，无需生物成像中的荧光标记，就可用纯光学的方法重建任意物体的全空间细节。通过设计焦斑尺寸更小、焦深以及焦距更大的平板衍射透镜以进一步提高基于平板衍射透镜扫描共焦显微镜的分辨率和成像能力。显微镜的这些新功能预期会添加到开发下一代激光扫描共聚焦显微镜的关键功能中。此外，在高密度数据存储中，透过或在扩散介质(如活细胞和组织)和多层介质(如记录材料)中实现超分辨聚焦还需要相关理论和技术的发展。因此，在不久的将来，这一领域的研究在广度和深度上的更进一步发展，可以为解决各种应用场景的关键问题提供基础和保障。