4p阶11度对称图

蓝婷 凌波

(云南民族大学数学与计算机科学学院,昆明,650504)

1 引言

本文涉及到的图都是有限的、连通的、简单的和无向的.对于一个图Γ,我们分别用VΓ,EΓ,AΓ和AutΓ表示其顶点集、边集、弧集和自同构群.若AutΓ分别传递作用在VΓ,EΓ和AΓ上,则分别称图Γ是点传递的、边传递的和弧传递的.对于图Γ的一个顶点序列(α0,α1,···,αs),如果满足{αi−1,αi}∈EΓ(1≤i≤s)和αi−1̸=αi+1,则称为图Γ的一条s−弧.若AutΓ传递作用在图Γ的s−弧集上,则称Γ为s−弧传递图.特别地,0−弧传递称为点传递,1−弧传递称为弧传递.若图Γ是s−弧传递(s≥1)但不是(s+1)−弧传递的,则称Γ是s−传递图.如果AutΓ在AΓ上作用正则,则称图Γ是1−弧正则的.

小度数弧传递图的分类是代数图论中的热门问题.例如,文献[1-3]分别给出了3度、5度和7度的4p阶对称图的分类.本文将进一步分类11度的4p阶对称图.

2 预备知识

正规商图是研究素数度弧传递图的重要方法.设Γ是一个G−点传递图,N(N̸=1)是G的非传递正规子群,用VΓN表示N−轨道集合.定义正规商图ΓN,其点集为VΓN,两顶点B,C相邻当且仅当B中存在点α,C中存在点β,使得{α,β}∈EΓ.如果Γ和ΓN有相同的度数,则称Γ是ΓN的正规覆盖.特别地,如果图Γ是连通的素数度的对称图,则根据文献[4]或者文献[5],可得到下面的引理:

引理1([4]或[5])设p为素数，Γ是连通的p度(G,s)−弧传递图,其中G≤AutΓ和s≥1.如果N是G的正规子群且在VΓ上至少有三个轨道,则N在VΓ上作用半正则且正规商图ΓN是连通的p度(G/N,s)−弧传递图.

根据文献[6]的Theorem 2.1和文献[7]的Corollary 1.3,我们可以知道11度弧传递图顶点稳定子群的结构.

引理2([6],[7])设图Γ是连通的11度(G,s)−传递图,其中G≤AutΓ和s≥1.令α∈VΓ,则s≤3且下列之一成立：

(1)若Gα可解,则|Gα||1100.进一步有,(s,Gα)在下表之中.

?

(2)若Gα不可解,则|Gα||216·38·54·72·11.进一步有,(s,Gα)在下表之中.

?

根据文献[8],可知两倍素数阶素数度对称图的分类.

引理3([8])设Σ是连通的奇素数p度2r阶对称图,其中r是素数.则下列之一成立.

(i)(r,p)=(7,3),AutΣ～=PGL(2,7)；

(ii)(r,p)=(11,5),AutΣ～=PGL(2,11)；

(iii)(r,p)̸=(7,3)和(11,5),AutΣ～=D2r:Zp.

根据文献[9,p.134-136],通过检验非交换单群的阶,有下面的引理.

引理4([9])设T是一个非交换单群,且满足44p||T|和|T||218·38·54·72·11·p,其中p是一个奇素数,则T在表1中.

表1 非交换单群T

证明根据非交换单群的分类,T有三种情况：零散单群、n级交错群和Lie型单群.

若T是零散单群,则直接检验零散单群的阶可知,满足条件的零散单群有：M11,M12,M22,M23,M24,J1,HS,McL,Suz,Co2,Co3.

若T是n级交错群,则由引理条件知|T|至多有六个素因子且11||T|,从而得到,T～=An,11≤n≤16.

若T是Lie型单群,则根据Lie型单群表可知Lie型单群有：PSL(d,rf)(d≥2),PSU(d,rf)(d≥3),PSp(2d,rf)(d≥2),PΩ+(2d,rf)(d≥4),PΩ−(2d,rf)(d≥4),PΩ(2d+1,rf)(d≥3),G2(rf)(d>4),F4(rf),E6(rf),E7(rf),E8(rf),Sz(22f+1),Ree(32f+1),2F4(22f+1),3D4(rf),2E6(rf),其中d和f是大于等于0的正整数.根据引理条件有,219,310,56,74和113不整除T的阶,从而知F4(rf),E6(rf),E7(rf),E8(rf)和2E6(rf)不符合条件.下面将对剩下的Lie型单群逐一讨论.

假设T=PSL(d,rf),其中d≥2.根据PSL(d,rf)的阶,得到rfd(d−1)/2整除|T|,再由引理的条件,进一步我们推出2≤d≤6.

当d=2时,T=PSL(2,rf),那么rf整除|T|.此时,若r>11,根据PSL(2,rf)的阶知这不可能.若r=11,有11f整除|T|,又113不整除T的阶,故f≤2.这时T可能为PSL(2,11)和PSL(2,112).检验PSL(2,11)和PSL(2,112)的阶,可知PSL(2,112)不符合条件.若r<11,那么r∈{2,3,5,7}.当r=2时,有2f整除|T|,又因为219不整除|T|,可得f≤18,此时T=PSL(2,2f)(f≤18).逐一验算它们的阶,我们得到只有PSL(2,25)符合条件.类似地分析,我们可将r∈{3,5,7}的情况排除掉.

当d=3时,T=PSL(3,rf).根据PSL(3,rf)的阶,我们得到r3f整除|T|.由引理条件知,r3f(r≥11)不能整除|T|.因此r∈{2,3,5,7}.若r=2,则有23f整除|T|.又因为219不整除|T|,因此f≤6.此时T=PSL(3,2f)(f≤6).逐一验算它们的阶,知无一满足条件.若p=3,则有33f整除|T|,310不整除|T|,可得到f≤3.此时T可能为PSL(3,3),PSL(3,9)和PSL(3,27).检验它们的阶,均不满足条件.同理可将r∈{5,7}的情况排除掉.

当d=4时,T=PSL(4,rf).根据PSL(4,rf)的阶,有r6f整除|T|.注意到56,74,113和r2(r>11)不整除|T|,因此有r∈{2,3}.当r=2时,26f整除|T|,又219不整除|T|,进一步可得到f≤3,此时T=PSL(4,2f)(f≤3).再检验这三个群的阶数,可知均不满足条件.当r=3时,36f整除|T|,又310不整除|T|,得到f=1.检验PSL(4,3)的阶,知PSL(4,3)不满足条件.

当d=5时,T=PSL(5,pf).根据PSL(5,rf)的阶,有r10f整除|T|.注意到310,56,74,113和r2(r>11)不整除|T|,因此可知只有r=2这种情况.进一步有,210f整除|T|,又219∤|T|,故f=1,此时T=PSL(5,2).检验PSL(5,2)的阶,知其不满足条件.

当d=6时,有T=PSL(6,rf),r15f整除|T|.注意到310,56,74,113和r2(r>11)不整除|T|,故r=2.又由215f整除|T|和219∤|T|,可得f=1.此时T可能为PSL(6,2),但由它的阶知其不满足条件.

假设T=PSU(d,rf),其中d≥3.根据PSU(d,rf)的阶,得到rfd(d−1)/2整除T的阶.又由引理条件有219,310,56,74,113和r2(r>11)不整除|T|,故3≤d≤6.

当d=3时,T=PSU(3,rf).根据PSU(3,rf)的阶,有r3f整除|T|.注意到113和r2(r>11)不整除|T|,有r∈{2,3,5,7}.当r=2时,23f整除|T|,又219||T|,我们可得f≤6.此时T=PSU(3,2f)(f≤6).检验它们的阶,知无一满足条件.

当d=4时,有T=PSU(4,rf),r6f整除|T|.又因为56,74,113和r2(r>11)不整除|T|,我们有r∈{2,3}.当r=2时,26f整除|T|,又219不整除|T|,可得f≤3,故T可能为PSU(4,2),PSU(4,4),PSU(4,8).又因为11整除|T|,通过计算阶可得PSU(4,2),PSU(4,4),PSU(4,8)都不满足条件.

当d=5时,有T=PSU(5,rf),r10f整除|T|.又因为310,56,74,113和r2(r>11)不整除|T|,故r=2.进而有210f整除|T|,f=1,T=PSU(5,2).检验PSU(5,2)的阶,知PSU(5,2)满足条件.

当d=6时,T=PSU(6,rf).由PSU(6,rf)的阶,有r15f整除|T|.又因为310,56,74,113和r2(r>11)不整除|T|,故r=2,即T=PSU(6,2f).进而根据PSU(6,2f)的阶,有215f整除|T|,f=1,T=PSU(6,2).检验PSU(6,2)的阶,知PSU(6,2)满足条件.

假设T=PSp(2d,rf),其中d≥2.根据PSp(2d,rf)的阶,有rfd2整除|T|,进而可得2≤d≤4.

当d=2时,有T=PSp(4,rf),r4f整除|T|.又因为74,113和r2(r>11)不整除|T|,我们有r∈{2,3,5}.当r=2时,24f整除|T|,又219∤|T|,可得f≤4.此时T=PSp(4,2f)(f≤4),但PSp(4,2f)(f≤4)的阶不被11整除,故不满足条件.当r=3时,T=PSp(4,3f),根据其阶有,34f整除|T|.又因为310不整除|T|,故可得f≤2.此时T=PSp(4,3f)(f≤2).注意到11整除|T|,但|PSp(4,3)|和|PSp(4,9)|不被11整除,故而排除掉.当r=5时,54f整除|T|,又因为56不整除|T|,从而得到f=1,进而有T=PSp(4,5).检验PSp(4,5)的阶,知|PSp(4,5)|不被11整除,因此不符合条件.

当d=3时,T=PSp(6,rf).根据PSp(6,rf)的阶,有r9f整除|T|.又因为56,74,113和r2(r>11)不整除|T|,我们有r∈{2,3}.当r=2时,29f整除|T|,又219∤|T|,可得f≤2,T=PSp(6,2f)(f≤2).检验它们的阶,知|PSp(6,2)|和|PSp(6,4)|不被11整除,故而不满足引理条件.当r=3时,T=PSp(6,3f),39f整除|T|.又310∤|T|,从而得到f=1.由PSp(6,2)的阶知,|PSp(6,2)|不被11整除,不满足引理条件.

当d=4时,T=PSp(8,rf),r16f整除|T|.又因为310,56,74,113和r2(r>11)不整除|T|,故r=2.进一步有,216f整除|T|,但219不整除|T|,因而可得f=1,T=PSp(8,2).由PSp(8,2)的阶知,|PSp(8,2)|不被11整除,不满足条件.

假设T=PΩ+(2d,rf),其中d≥4.则可得到rfd(d−1)整除|T|.又因为219,310,56,74,113和r2(r>11)不整除|T|,得到d=4,r=2和f=1,即T=PΩ+(8,2).但是PΩ+(8,2)的阶不被11整除,因而不满足条件.

假设T=PΩ−(2d,rf),其中d≥4.则可得到rfd(d−1)整除|T|.又因为219,310,56,74,113和r2(r>11)不整除|T|,得到d=4,r=2和f=1,即T=PΩ−(8,2).但是PΩ−(8,2)的阶不被11整除,因而不满足条件.

假设T=PΩ(2d+1,rf),其中d≥3.则可得到rfd2整除|T|.又因为219,310,56,74,113和r2(r>11)不整除|T|,得到d∈{3,4}和r∈{2,3}.当d=3时,有T=PΩ(7,rf),r9f整除|T|,从而T=PΩ(7,2f)(f≤2)和PΩ(7,3).但PΩ(7,2f)(f≤2)和PΩ(7,3)的阶均不被11整除,因此不满足条件.当d=4时,T=PΩ(9,rf),又因为219和310不整除T的阶,故有r=2和f=1,T=PΩ(9,2).但11不整除PΩ(9,2)的阶,故不满足条件.

假设T=G2(rf),其中rf>2.由G2(rf)的阶,有r6f整除|T|.根据219,310,56,74,113和r2(r>11)不整除|T|,推出r∈{2,3}.当r=2时,2≤f≤3,T为G2(4)或G2(8).但它们的阶均不被11整除,不满足条件.当r=3时,有36f整除|T|,又310不整除|T|,推出f=1,T=G2(3).检验G2(3)的阶,知其不满足条件.

假设T=Sz(22f+1),则有22(2f+1)整除|T|.又因为219不整除|T|,故f≤4,从而T为Sz(2),Sz(8),Sz(32),Sz(128)或Sz(512).但这些群的阶均不被11整除,不满足条件.

假设T=Ree(32f+1).根据Ree(32f+1)的阶,有33(2f+1)整除|T|.又310不整除|T|,故f∈{0,1},从而T为Ree(3)或Ree(33).但它们的阶均不被11整除,故不满足条件.

假设T=2F4(22f+1),则有212(2f+1)整除T的阶.又因为219不整除|T|,因而T只有2F4(2).但|2F4(2)|不被11整除,故不满足条件.

假设T=3D4(rf),则有r12f整除T的阶.又因为219,310,56,74,113和r2(r>11)不整除|T|,故T只有2D4(2).但2D4(2)的阶不被11整除,故不满足条件.

3 主要结果

定理1设Γ是连通的11度4p阶对称图,其中p是素数.则Γ～=K12.

证明若p=2,则Γ为8阶11度对称图,这显然不可能.若p=3,则Γ为12阶11度对称图,即有Γ～=K12.下面讨论p>3的情况.

设A=AutΓ,N是A的极小正规子群,α∈VΓ.由引理2,|Aα|整除216·38·54·72·11,因此有|A|整除218·38·54·72·11p,其中p是素数.

假设N是可解的,则N是一个初等交换群.令其中r是素数和d≥1是一个正整数.显然N在VΓ上至少有3个轨道,由引理1,知N半正则,进而得到|N|=|Zr|d整除4p,因此如果N～=Zp,由引理1知,正规商图ΓN是4阶的11度A/N−弧传递图,这显然不可能.如果由引理1知,正规商图ΓN是p阶的11度A/N−弧传递图.注意到奇数度对称图的阶数是偶数,故而矛盾.因此N～=Z2,由引理1知,正规商图ΓN是2p阶11度A/N−弧传递图,其中A/N≤AutΓN.由引理3,有或CD2p.若则Γ是K11,11的一个正规Z2−覆盖,根据文献[10],知这样的覆盖图不存在.若又因为ΓN为A/N−弧传递图,有11·2p||A/N|,进而从而Γ是1-弧正则图.由文献[11]知,该图不存在.

因此N是不可解的.设N=Tm,其中T是非交换单群且m是大于等于1的正整数.接下来,我们证明N在VΓ上至多有两个轨道,N不是半正则的且44||N|,以及N是A的唯一的极小正规子群且m=1.

如果N半正则,那么|N|=|T|m整除4p.根据Burnside定理,即两个素因子阶的群可解,我们有N是可解的,矛盾.于是N不是半正则的,即Nα̸=1.因此由引理1可推出N在VΓ上至多有两个轨道.因为Γ连通和N◁A,我们得到从而11||Nα|.注意到N在VΓ上至多有两个轨道,有|N|=2p|Nα|或4p|Nα|,故p||N|.因此44p||N|,进而,44p||T|和(44p)m||N|.因为

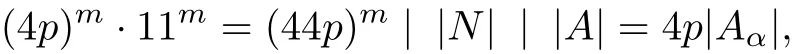
我们有(4p)m−1·11m||Aα|.由引理2知,112∤|Aα|,因此m=1.

令C=CA(N).假设C̸=1.因为A无可解正规子群,因而C是不可解的.若Cα=1,则|C|整除4p,得到C是可解的,从而矛盾,故Cα̸=1.又因为C◁A,由连通性我们得到进一步有11||Cα|.由C∩N=1,有C×N◁A,进而,这与引理2矛盾.因此C=1,这意味着N是A的唯一的极小正规子群.

上面我们证明了N在VΓ上至多有两个轨道,N=T是一个非交换单群且44p||N|.此外,由引理2知|A|=|VΓ||Aα||218·38·54·72·11·p,故|N||218·38·54·72·11·p.因此N的可能性由引理4决定,并由表1给出.注意到N在VΓ上至多有两个轨道,我们有|N:Nα|=2p或4p.

假设N～=M11,则|N|=24·32·5·11.注意到11||Nα|和假设条件p>3,我们有p=5.根据Atlas[12]知,M11极大子群的指数为11,12,55,66,165.因此M11没有指数为2p=10或4p=20的子群,矛盾.对于表1中剩余的单群,同理,根据Atlas[12]或Magma计算,可以知道N没有指数为2p或4p的子群,矛盾.