Ground State Solutions for a Fourth Order Quasilinear Elliptic Equation
2021-08-23HuDieZhangQi
Hu Die Zhang Qi
(School of Mathematics and Statistics,Central South University,Changsha,Hunan 410083,China)
Abstract This paper studies the following fourth order quasilinear elliptic equation
Key words Fourth order quasilinear elliptic equation Ground state solution of Nehari-Pohoz̆aev type Variational method Corresponding author:Zhang Qi;E-mail:zq8910@csu.edu.cn
1 Introduction
Fourth order problems involving biharmonic operator have been extensively investigated since Lazer and Mckenna[1]proposed the following equation

where Ω⊂RNis a bounded domain andc∈R,to study large amplitude periodic oscillations and travelling waves in the well-known suspension bridge problem.In recent years,by virtue of the modern variational theory,problem(1.1)and its variants have attracted massive research interests.For instance,the fourth order elliptic equation
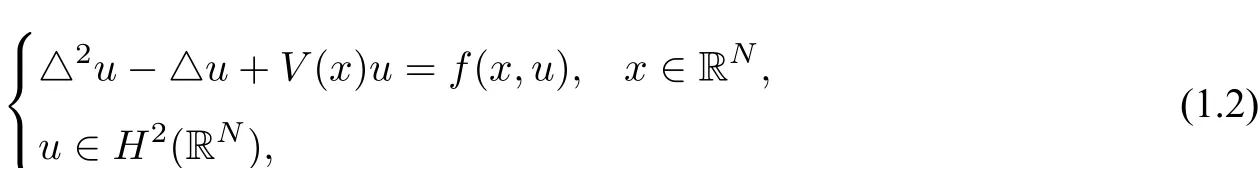
was studied by many researchers and a series of results was obtained by making use of various weak versions of the Ambrosetti-Rabinowitz condition.For example,In[4],Yin and Wu obtained a sequence of high energy solutions to(1.2)with the nonlinearityf(x,u)odd and superlinear at infinity andVsatisfying a weakened coercive condition.Later in[11],withf(x,u)sublinear,Ye and Tang unified and improved their results by means of the minimax method in critical point theory.Soon after[11],Liu et al.[12]also studied the existence and multiplicity of nontrivial solutions for peoblem(1.2)with a large parameter(see also[14]).And then,Zhang et al.in[13,15,16]studied(1.2)further under some weaker assumptions on the potentialV(x)and the nonlinearityf(x,u);they established the existence of infinitely many solutions in[13,15]and the existence of ground state solutions in[16],respectively.Recently,Chen et al.[3]firstly investigated the modified fourth order quasilinear elliptic equation:

where the nonlinearityf(x,u)is 4-superlinear and the potentialVis positive and coercive.They obtained the existence of nontrivial solutions and a sequence of high energy solutions.After the work of[3],problem(1.3)has attracted the interest of several researchers such as[2,3,5,6,17,19]which obtained some nontrivial or multiple solutions.For example,Cheng and Tang in[6]obtained a sequence of high energy solutions with the potential being sign-changing and satisfying the almost coercive condition borrowed from[7].
Although there are many papers studying the nontrivial solutions of fourth order equation(1.3),as far as we know,there is no result studying the ground state solutions for it until now.Motivated by the aforementioned works,in this paper,using the Nehari-Pohoz̆aev manifold method used in[8,10,18,20,21],we consider the existence of ground state solutions to the following equation:
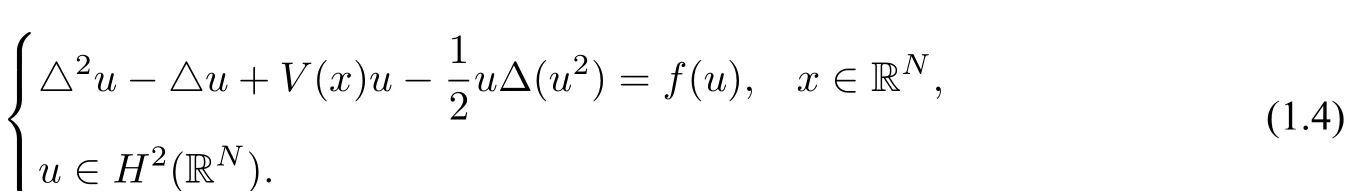
Firstly,we need some assumptions onVandf:


Remark 1.1(1)Conditions(V3)and(F4)are borrowed from[18].It is easy to verify that the condition(F4)implies the usual Nehari type conditionis nondecreasing on(−∞,0)∪(0,+∞).
But(F4)is weaker thanFor example,the function
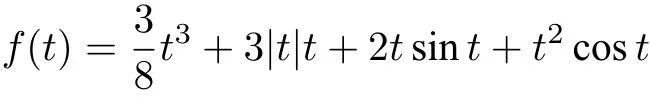
satisfies(F4)but not
(2)Functions satisfiying(V1)−(V3)do exist.For instance,

wherem≥2,a>b>0 and 2bm(m+2+N) Throughout the paper we use the following notations. •H2(RN)denotes the usual Sobolev space equipped with the inner product and norm •Ls(RN)(1≤s<∞)denotes the Lebesgue space with the norm •For anyu∈H2(RN){0}, •For anyx∈RNandr>0,Br(x):={y∈RN:|y−x| •C1,C2,...denote positive constants possibly different in different places; •2*ifN>4 and 2∗=+∞ifN≤4. From the assumptions onVandfand lemma 2.2 in[3],we get that the energy functional defined inH2(RN)by If the potentialV(x)≡then(1.4)becomes the autonomous form with energy functional: It is easy to verify that every solutionuof(1.4)or(1.6)satisfies and respectively. Now we are ready to state the main results of this paper.Let and Theorem 1.1Assume thatVandfsatisfy(V1)−(V3)and(F1)−(F4).Then problem(1.4)has a solutionsuch that As a consequence of Theorem 1.1,we can prove the following theorem. Theorem 1.2Assume thatfsatisfies(F1)−(F4).Then problem(1.6)has a solutionsuch that In this section,we firstly give some useful lemmas and then prove Theorem 1.2. Lemma 2.1For allt∈[0,1)∪(1,+∞),the following inequalities hold: Moreover,t>0,(V3),(F1)and(F4)imply that and ProofThe proof of the inequalities(2.1)and(2.2)are simple,so we omit it here.It is evident that(2.3)holds forτ=0.Forτ̸=0,let then from(F4),one has It follows thatξ(t)≥ξ(1)=0 fort>0.This,together with(2.4),(2.5),implies(2.3). Lemma 2.2Assume that(V1),(V3),(F1)and(F4)hold.Then ProofAccording to the Hardy inequality,we have Note that Thus,by(1.5),(1.7),(2.1),(2.2),(2.3),(2.7)and(2.8),one has This shows that(2.6)holds. From Lemma 2.2,we have the following two corollaries. Corollary 2.3Assume that(F1),(F4)hold.Then Corollary 2.4Assume that(V3),(F1)and(F4)hold.Then for allu∈M, Lemma 2.5Assume that(V1)−(V3)hold.Then there exist two constantsγ1,γ2>0 such that ProofUsing(V2)and lettingt=0 ort→∞in(2.2),one get Thus it follows from(2.7)and(2.12)that and Then(2.13)and(2.14)imply that(2.11)holds. To show M̸=∅,we need the following Lemma 2.6Assume that(V1)−(V3)and(F1)−(F4)hold.Then for anyu∈H2(RN){0},there exists a uniquetu>0 such thatutu∈M. ProofLetu∈H2(RN){0}be fixed and define a functionη(t):=I(ut)on(0,∞).Clearly,by(1.7),(1)and(2.8),we have Using(V1),(V2),(F1),(F3)and(2.8),it is easy to verify that limt→0η(t)=0,η(t)>0 fort>0 small enough andη(t)<0 fortlarge enough.Therefore,maxt∈[0.∞)η(t)is achieved at sometu>0 such thatη′(tu)=0 andutu∈M. Next we claim thattuis unique for anyu∈H2(RN){0}.In fact,for any givenu∈H2(RN){0},lett1,t2>0 such thatut1,ut2∈M and Φ(ut1)=Φ(ut2)=0.Then by(2.6),we have (2.16)and(2.17)imply thatt1=t2.So,tu>0 is unique for anyu∈H2(RN){0}. Corollary 2.7Assume that(F1)−(F4)hold.Then for anyu∈H2(RN){0},there exists a uniquetu>0 such that Corollary 2.4 and Lemma 2.6 imply thatM̸=∅and the following lemma. Lemma 2.8Assume that(V1)−(V3)and(F1)−(F4)hold.Then Lemma 2.9Assume thatN≤6.Ifun⇀uinH2(RN),then along a subsequence of{un}there holds ProofWe firstly choose numbersqandrsuch thatFor everyu∈H2(RN),since and which implies{un|∇un|}is bounded inL2(RN). Moreover,since the embeddingis compact,up to a subsequence we have Therefore,by the Brezis-Lieb Lemma in[9],we obtain the desired result.Lemma 2.9 and condition(F1)yield the following lemma. Lemma 2.10Ift hen,up to a subsequence,the following B-L splitting hold. Lemma 2.11Assume that(V1)−(V3)and(F1)−(F4)hold.Then(i)there exists aρ0>0 such that‖u‖≥ρ0,∀u∈M;(ii)m=infu∈M I(u)>0. Proof(i)Since∀u∈M,Φ(u)=0.From(F1),(F2),(1.7),(2.11)and the Sobolev embedding theorem,one has which implies whereωNdenotes the volume of the unit ball of RN.Foru∈M,let From the result of(i)we know that‖∇u‖2̸=0,so thetumakes sense.Making use of the Hölder inequality and the Sobolev embedding theorem,we get Then from(2.6),(2.8),(2.25),(2.26)and the Sobolev embedding theorem,we have This shows thatm=infu∈M I(u)>0. Lemma 2.12Assume that(F1)−(F4)hold.Thenis achieved. Hence,{un}is bounded inH2(RN).Thanks to Lions’concentration compactness principle[9],from(F1),(F2),Lemma 2.11(i)and Lemma 2.5,one can easily prove that there exist aδ>0 and a sequence and LetThen(2.31)and Lemma 2.10 yield and Set Lettingt→0 in(2.3)we get Hence, From(2.30),(2.32),(2.33)and(2.34),one has If there exists a subsequence{ωni}of{ωn}such thatωni=0,then going to this subsequence,we have which contradicts with(2.36)and(2.37),and implies the desired resultHence,asin view of Corollary 2.7,there exists asuch thatFrom(F1),(2.9)and(2.34),one has which implies Lemma 2.13Assume that(V1)−(V3)and(F1)−(F4)hold.Ifis a critical point ofI. ProofAssume that,then there exist aδ>0 and a0 such that First,applying the theory of real variable function we can prove that In view of Lemma 2.2,one has Let andS:=Lemma 2.3 in[9]leads to a deformationη∈C([0,1]×H2(RN),H2(RN))such that i)η(1,u)=uifI(u) ii)η(1,⊂Im−ε; iii)I(η(1,u))≤I(u),∀u∈H2(RN); iv)η(1,u)is a homeomorphism ofH2(RN). On the other hand,by iii)and(2.42),one has where Combining(2.44)with(2.45),we have Defineζ(t):=It follows from(2.42)and i)thatt=T2,which,together with(2.43),implies Sinceζ(t)is continuous on(0,∞),we have thatfor somt0∈[T1,T2],which contradicts with the definition ofm. Proof of Theorem 1.2In view of Lemmas 2.8 and 2.12,there exists asuch that This shows thatˆuis a ground state soution of the Pohoz̆aev type for(1.6). In this section,we give the proof of Theorem 1.1.From now on we always assume thatTheorem 1.1 is contained in Theorem 1.2). Lemma 3.1Assume that(V1)−(V3)and(F1)−(F4)hold.Then ProofIn view of Theorem 1.2,has a minimizer In view of Lemma 2.6,there exists at0>0 such thatThus,it follows from(V2),(1),(2.9)and(3.1)that Lemma 3.2Assume that(V1)−(V3)and(F1)−(F4)hold.Thenmis achieved. ProofIn view of Lemmas 2.6 and 2.11,we haveM̸=∅andm>0.Let{un}⊂Mbe a sequence such thatI(un)→m.Since Φ(un)=0,then it follows from(2.6)that ast→0 This shows that{un}is bounded inH2(RN).Passing to a subsequence,we have There are two possible cases about From(1.5),(1),(1.7),(1.7)and(3.4),we can get And from Lemma 2.11(i),(1.7)and(3.5),we have Using(F1),(F2),(3.6)and Lions’concentration compactness principle in[9],similar to the proof of Lemma 2.12,we can show that there exist aδ>0 and a sequence{yn}⊆RNsuch thatδ.LetThen we haveand Therefore,there exists aˆu∈H2(RN){0}such that,passing to a subsequence, If there exists a subsequence{ωni}of{ωn}such thatωni=0,then going to this subsequence,we have Next,we assume thatωn̸=0.Similar to the latter part proof of Lemma 2.12,we can show thatMoreover,asin view of Corollary 2.7,there exists asuch thatFrom Lemma 3.1,(F1),(2.9),(2.34)and(3.7),one has which implies(3.10)holds.In view of Lemma 2.6,there exists asuch thatIt follows from(V2),(2.9)and(3.10)that This shows thatmis achieved at and Set Lettingt→0 in(2.2)we get From(2.7),(2.35),(3.13)and(3.14),it holds that SinceI(un)→mand Φ(un)=0,it follows from(3.11),(3.12)and(3.13)that If there is a subsequence{νni}of{νn}such thatνni=0,then going to this subsequence,we have which implies the conclusion of Lemma 3.2 holds.Next,we assume thatνn̸=0.We claim thatOtherwise,if,then(3.16)implies Φ(νn)<0 for largen.In view of Lemma 2.6,there exists atn>0 such that(νn)tn∈M.From(2.6),(3.13)and(3.16),we obtain which implies(3.17)also holds. Proof of Theorem 1.1In view of Lemmas 2.8,2.13 and 3.2,there exists asuch that This shows that¯uis a ground state solution of(1.4). The authors are grateful to the anonymous referees for their carefully reading this paper and giving valuable comments and advices.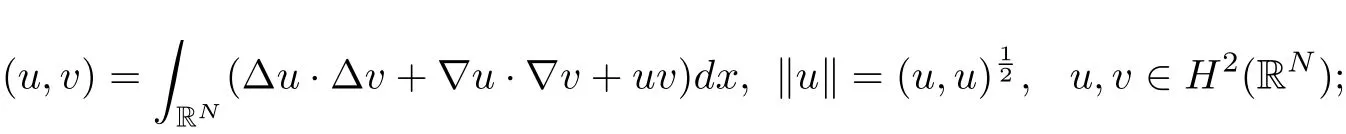

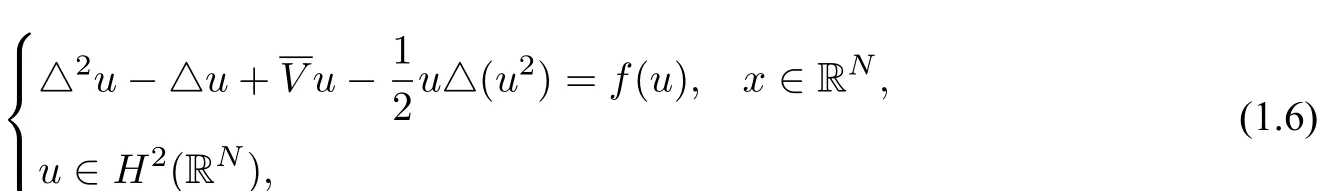

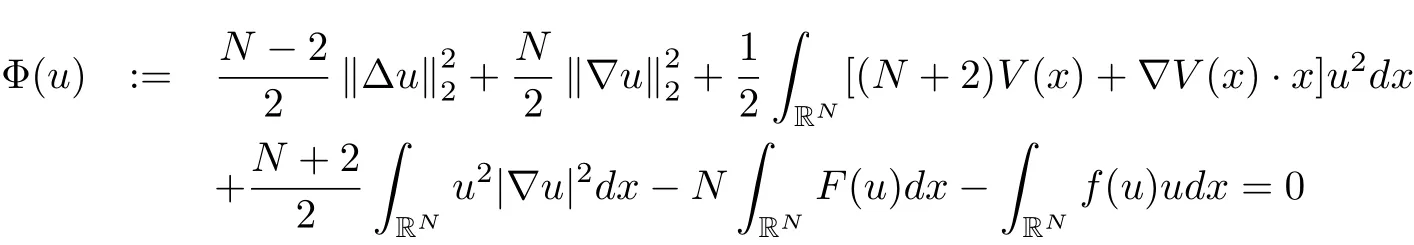

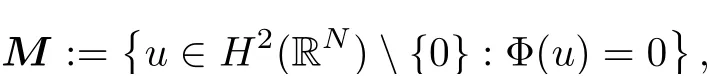



2 Some preliminaries

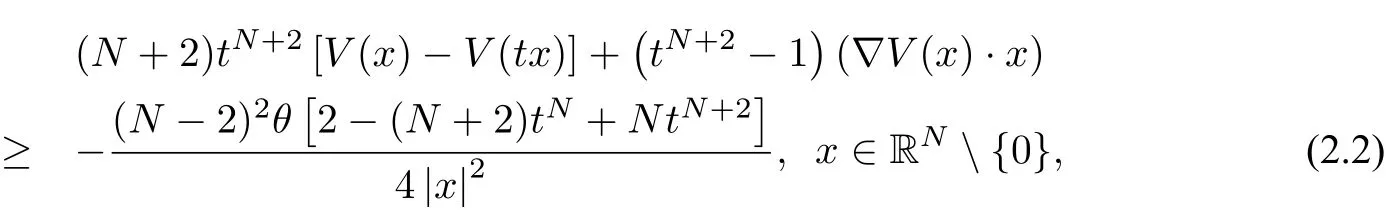

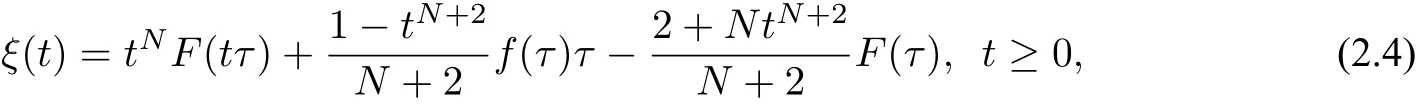

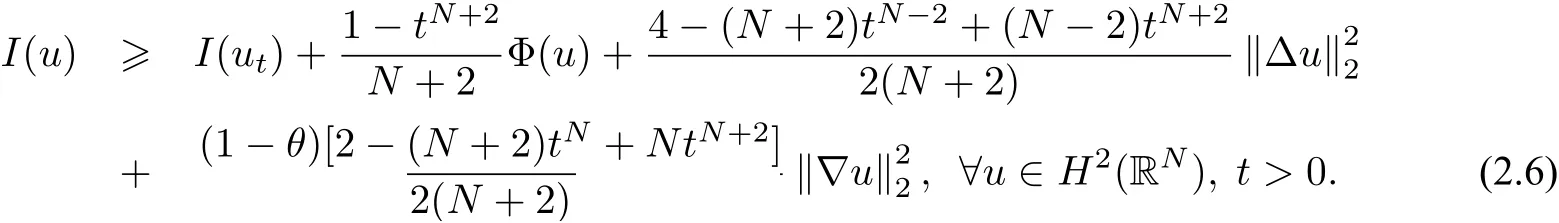

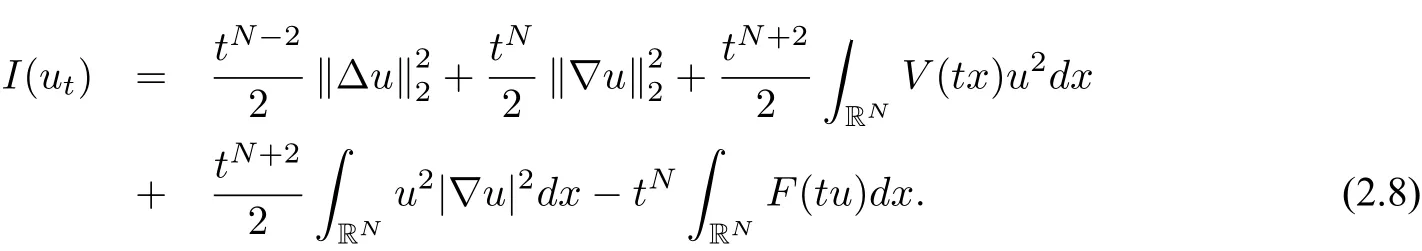





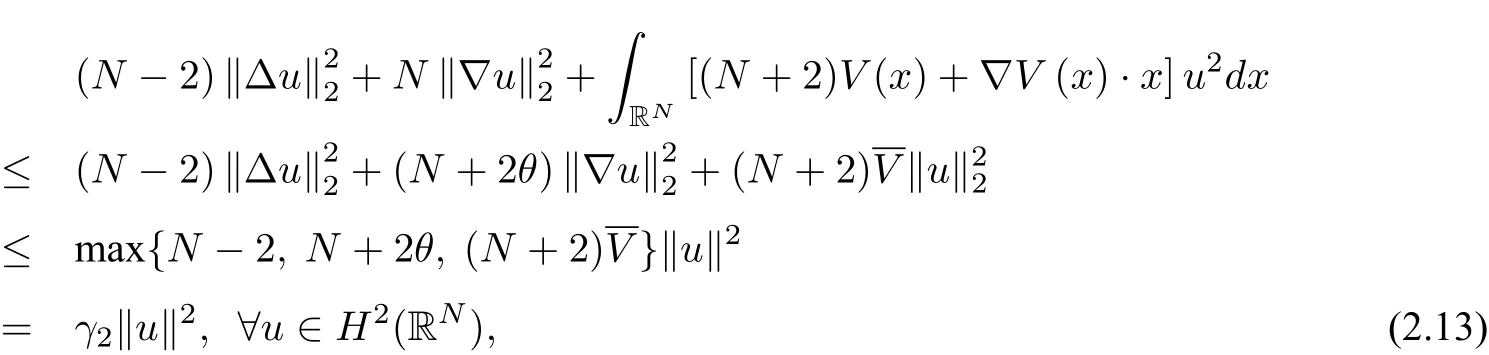






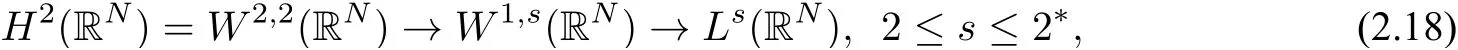




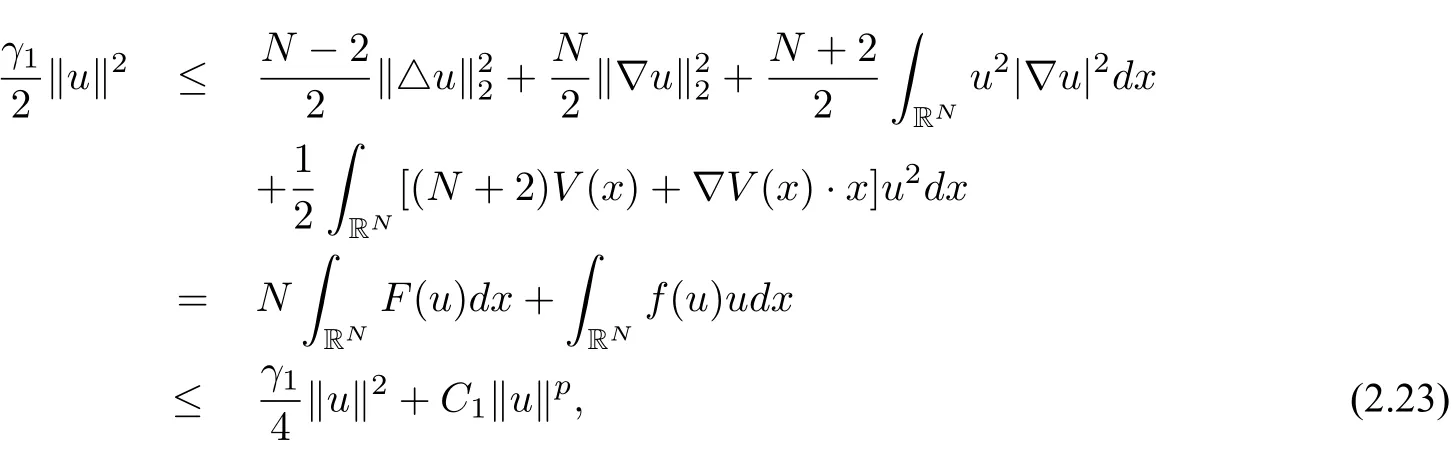
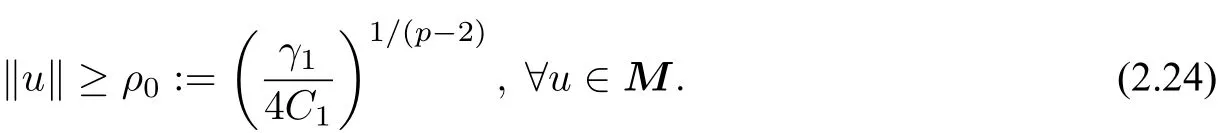
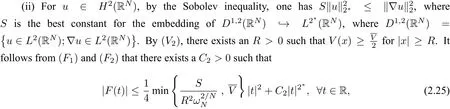
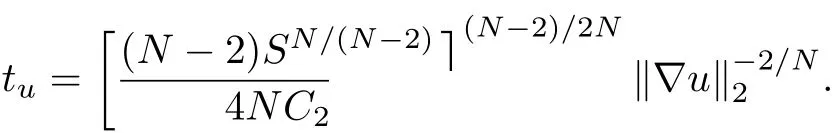









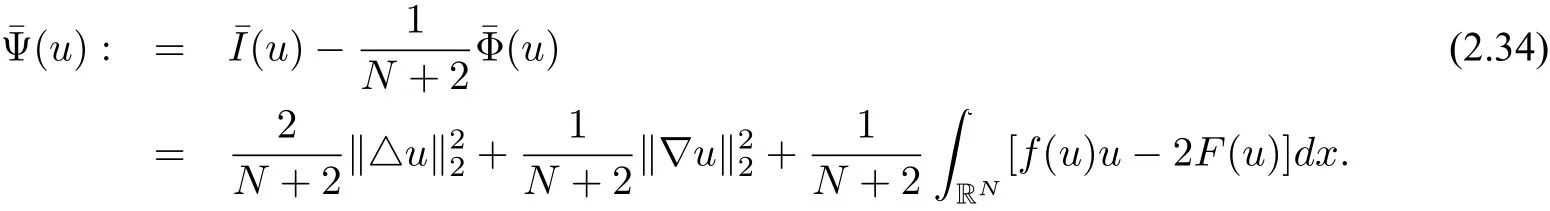

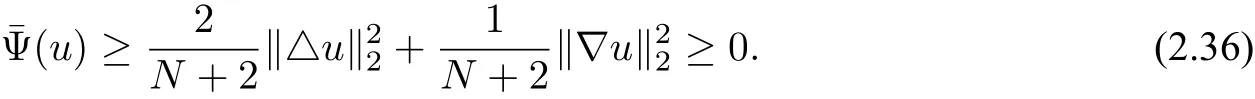




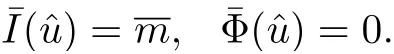





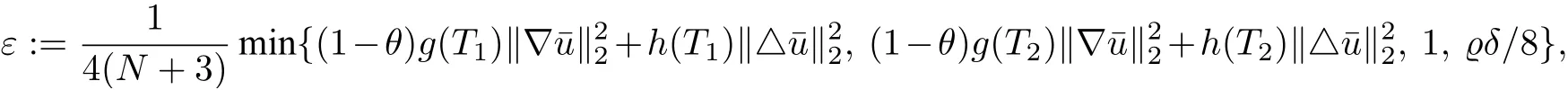






3 Ground state solutions

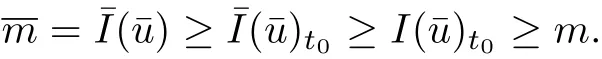
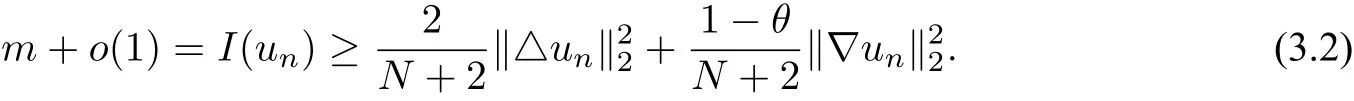








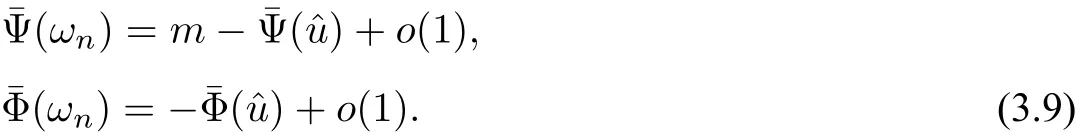








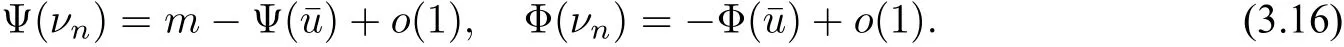


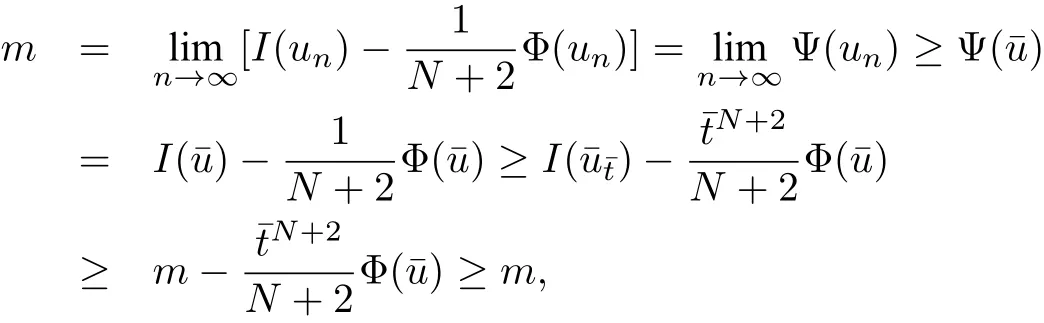
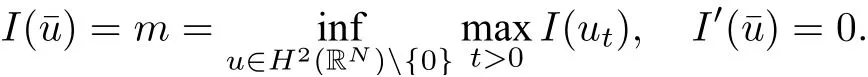
4 Acknowledgements
