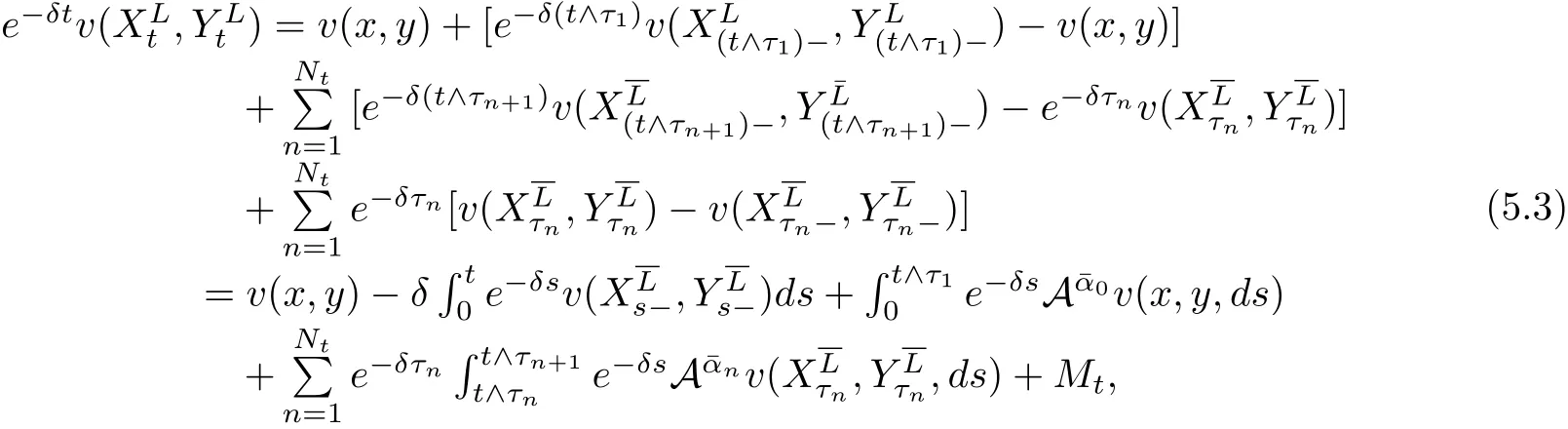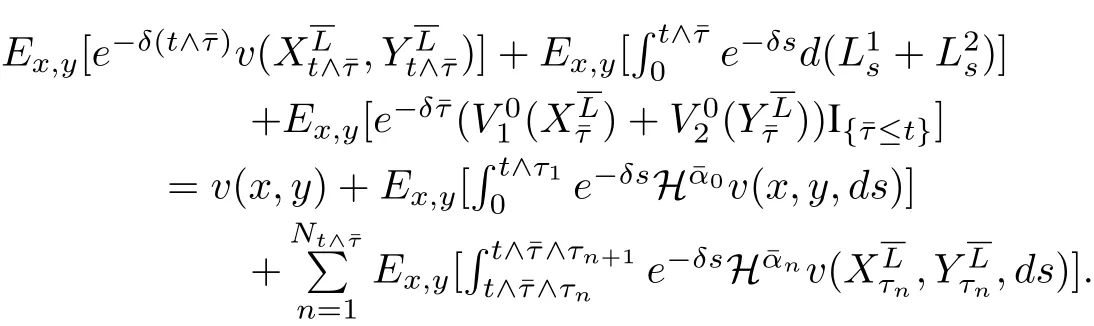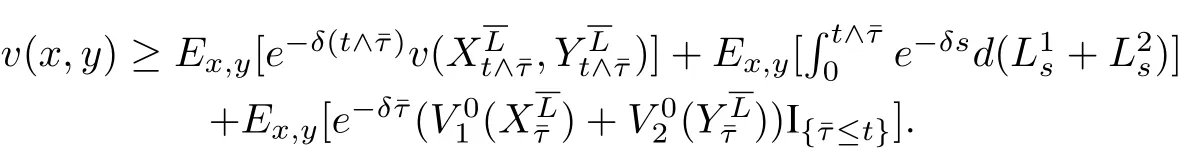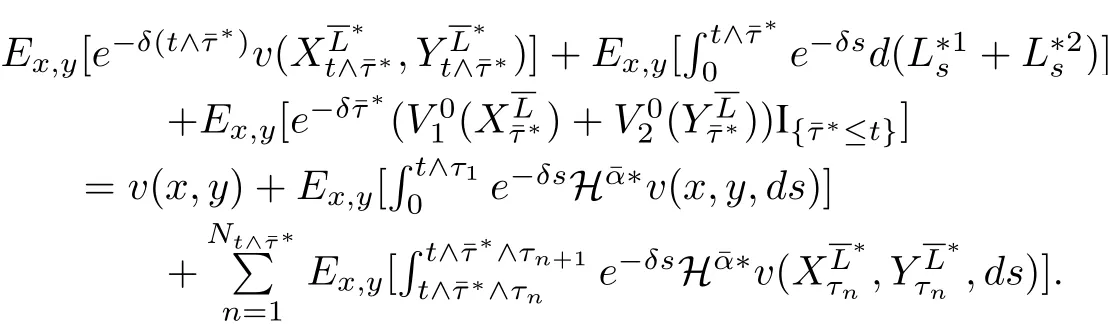两个合作保险公司的最优分红问题
2021-08-23冀宇轩刘国欣
冀宇轩 刘国欣
(河北工业大学理学院,天津,300401)
1 引言
风险模型最早由Lundberg提出,并由Cramer进行严格化.早期风险理论的主要研究问题是破产概率.1957年,De Finetti[1]在第15届国际精算学大会(纽约)上提出了最优分红问题,即最大化破产前期望折现分红,给出了一种更加“现实”的稳定性判据,并在简单的离散风险模型下研究了最优分红策略问题,证明了最优分红策略是障碍(barrier)策略,即当公司盈余额超过某一水平时,超出部分应全部进行分红.1969年,Gerber[2]用相关离散问题取极限的方法证明了在复合Poisson模型下,公司的最优分红策略一般为波段(band)策略.其后30多年的时间里最优分红策略问题的研究进展缓慢,直至上世纪90年代随机控制理论和方法的突破为最优分红策略研究提供了有效的工具.正如Borch在1967年的伦敦皇家统计学会会议上的报告指出的,随机控制理论好像是为精算学量身定做的数学工具.关于复合泊松模型的分红问题先驱性的工作见Buhlmann[3]和Gerber[4].直到今天,最优分红问题已经发展成一个需要分析、概率和随机控制学科交叉的丰富且富于挑战性的研究领域.关于最优分红问题的发展现状,可参见Schmidli[5]与Azcue和Muler[6]的两本专著及其参考文献.
近些年,二维风险模型的最优分红问题引起了广泛兴趣.二维问题可以更好地反应两个公司或一个公司中两个项目之间的关系,具有更加实际的意义.Asmussen和Albrecher[7]中详细地介绍了二维经典风险模型及相应破产问题及分红问题.Albrecher等[8]研究了二维经典风险模型下两个合作的保险公司的最优分红问题,但他们限定两个公司的盈余过程是相互独立的.
本文同样研究二维经典风险模型下两个合作保险公司的最优分红问题,但去掉了两个公司的盈余过程是相互独立的限制.本文首先给出模型,建立相应的二维最优分红问题.其次,给出值函数的基本性质,特别是给出可行策略的分析刻画,使我们可以更好地利用PDMP理论.最后,利用Liu等在[9]中给出的测度值生成元理论得到测度值DPE,证明了验证定理.
2 模型与分红问题
假设两个保险公司的盈余过程分别为
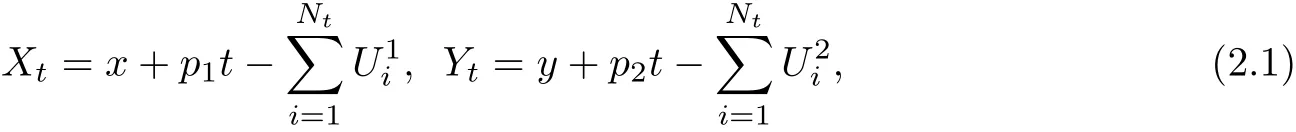
其中,x和y是各自的初始盈余;p1和p2是各自的保费收入率是公司k的第i次索赔大小,k=1,2,服从共同的联合分布F(x,y).Nt是强度为λ的泊松过程.假定Nt和随机变量是相互独立的.
两个保险公司的合作准则为:如果公司一的当前盈余为负,只要公司二可以支付公司一的实际赤字,即支付赤字后自己不会破产,就应立即支付公司一的赤字;反之亦然.当一个公司的当前盈余为负且另一个公司无法支付它的赤字,那么这个公司立即破产,另一个盈余为正的公司继续运营.
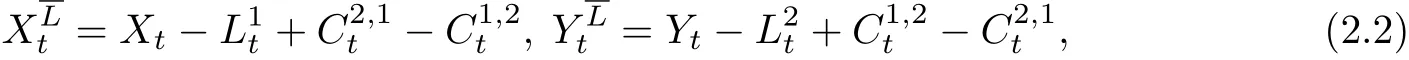
其中
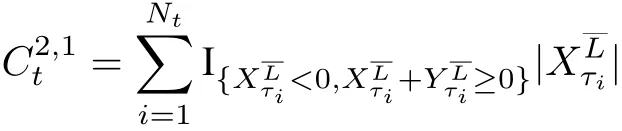
表示在时刻t,为了支付公司一的亏损,由公司二转移给公司一的累积盈余,

表示在时刻t,为了支付公司一的亏损,由公司二转移给公司一的累积盈余.上式中I{·}表示示性函数.
定义¯τ为破产时刻,表示有一个保险公司资产小于0,或两个公司资产都小于0的时刻,严格地说,
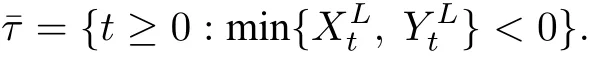

用Πx,y表示初始盈余时,所有的可行分红策略的集合.在初始盈余水平的前提条件下,我们可以写出该问题的最优值函数,如下:

其中,
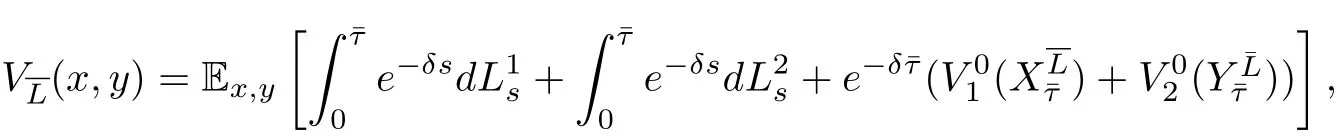
上式中δ>0是折现因子,分别为公司一与公司二单独运营时的最优分红值函数.
3 值函数性质与策略刻画
命题1∀x,y>0,最优值函数V(x,y)有良好定义,且满足

命题2最优值函数V(x,y)分别关于x,y是单调递增的,局部Lipschitz连续,且满足∀(x,y)∈有

和

上述命题的证明与Albrecher等[10]类似.
设Ω是一个有左右极限的路径的集合,(Ω,F,P)是具有由过程{(Xt,Yt)}生成的σ-代数流{Ft}的完备概率空间.定义一个推移算子θt:对s,t∈R+,ω∈Ω,有θt◦ωt=ωs+t.对∀x,y≥0,Ux,y为可测函数α:的集合,满足:
(1)α(x,y,t)关于t非降,左连右极,α(x,y,0)=0;
(2)α1(x,y,t) 定理1分红策略L∈Πx,y可行当且仅当存在两个可测函数α1(x,y,t)和α2(x,y,t),对以及Fτn×B(R+)-可测函数使得 其中¯α(t)=(α1(x,y,t),α2(x,y,t)).τi表示第i个索赔的到达时刻.称为马氏策略.若受控盈余过程是时齐的强马氏过程,则相应的可行策略L称为平稳马氏策略. 定义1若受控盈余过程是强马氏过程,则相应的可行策略 令M为Borel−可测函数l:的集合,满足 定理2可行策略为平稳马氏策略当且仅当存在函数l1,l2∈M,满足 定理1与定理2的证明分别类似于Liu等[11]中命题2.1与定理2.4的证明. 定理3(动态规划原理(DPP))对∀x,y≥0,任意停时T,有 证明由于自然流{Ft}为跳流,因此对任意停时T,存在t,使 得因此仅对固定时刻t≥0证明. 令 由最优值函数定义,有V(x,y)≤v(x,y,t). 再证V(x,y)≥v(x,y,t).任意给定ε>0,取一个可行策略使得 故V(x,y)≥v(x,y,t). 综上,V(x,y)=v(x,y,t).使得V(x,y)=则∀x,y≥0,∀t>0有 定理4(动态规划方程(DPE))假定存在一个可行策略 其中, 证明由动态规划原理,得 由Stieltjes积分分部积分公式及(4.3)可得 其中, 综合(4.4)和(4.5)式可得 定理5(验证定理)假设可测函数v是测度值DPE的解,满足∀x,y,t≥0, 证明对任意满足(3.1)的可行策略由Stieltjes分部积分公式,有 其中 为零初值鞅.由(5.3)可得 由于v是测度值DPE的解,因此所以有 令t→∞得,因此 从(4.2)和(5.1)可得,H¯α∗v(x,y,t)=0,因此 令t→∞得,因此 证毕.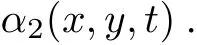


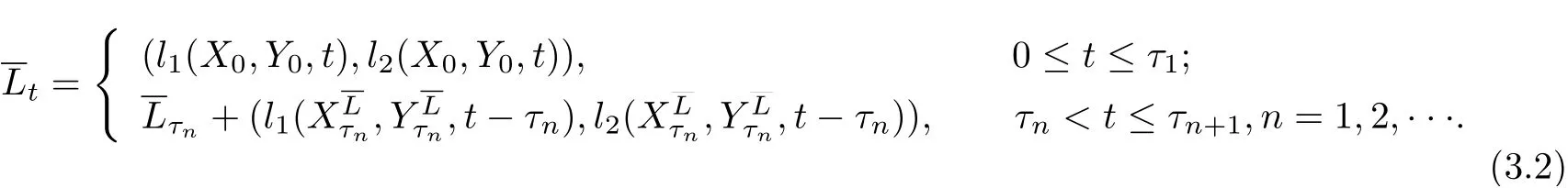
4 测度值动态规划方程
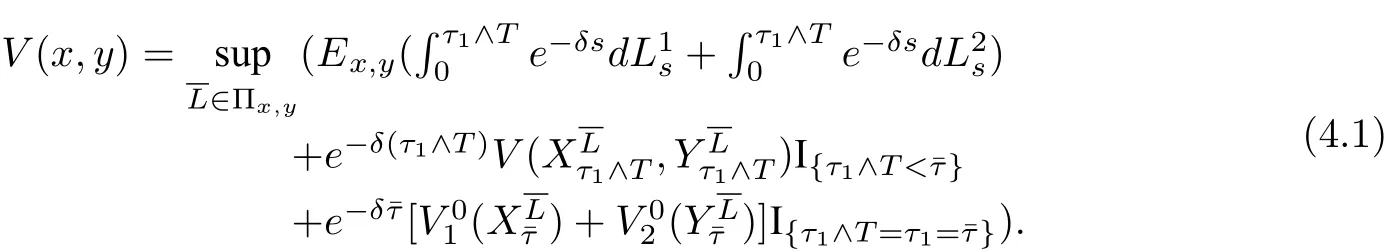
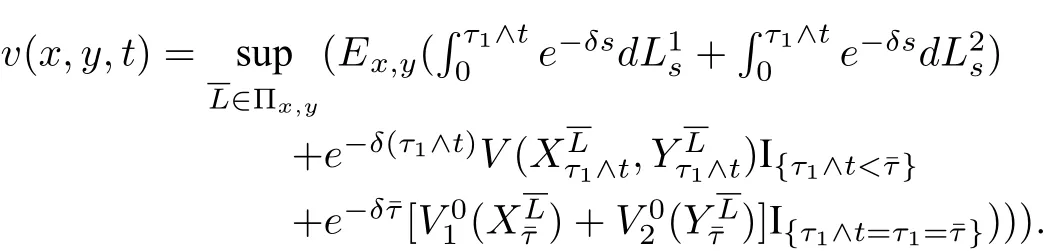



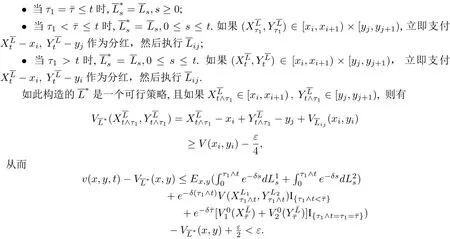







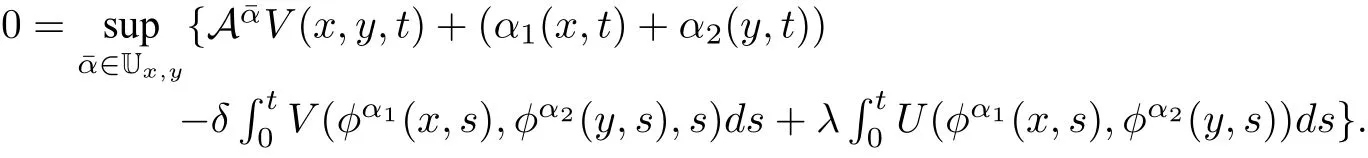
5 验证定理