基于ARMA模型的水文序列相依变异分级方法及验证

谢 平，霍竞群，桑燕芳，吴林倩，李雅晴，牛静怡

（1.武汉大学水资源与水电工程科学国家重点实验室，湖北武汉 430072；2.中国科学院地理科学与资源研究所陆地水循环与地表过程重点实验室，北京 100101）

1 研究背景

水文时间序列分析是深入了解水文现象特点与性质的重要途径，以及探究水文过程复杂变化规律的关键方法［1-2］。长久以来，对水文时间序列的认识与研究都是基于一致性假设（即物理成因不变）的基本条件开展的［1］。然而，受自然因素与人为因素等的影响，许多流域和地区的水文水资源状况发生了很大改变，导致水文时间序列不再全部满足一致性假设［3-4］，即发生了水文变异［5］，表现为统计规律随时间发生明显改变，且任意时刻数值均与前期时间内的历史值有关［6］。

依据水文变异的具体表现形式与水文序列参数的变化特征，又可分为跳跃、趋势、周期以及相依变异等［7］。其中，相依变异是水文变异的一种常见形式，表现为水文序列后一数据与紧邻的前一（几）数据具有成因、数值等方面的继承性［2］。当前，对水文序列中相依变异成分的研究和分析主要是基于数理统计方法进行［8-9］，如Hurst系数法［10-11］、极差和轮次分析法［12］、自相关分析法和谱分析法［13］等。然而，这些方法主要针对相依变异形式的识别和检验，但对相依变异程度进行量化的研究则很少涉及。在实际的水文统计分析与计算中，不仅要明确水文序列是否发生了相依变异，还要判定相依变异的强弱程度，如果未对相依变异的显著性进行定量评估，可能会对水资源安全评估以及水利工程建设等工作造成较大影响。相关系数可以描述序列间相关程度，其绝对值越大，则序列间的相关性越强，故可将相关系数作为度量水文变异程度的指标［14］。

常规的时间序列模型包括自回归模型、滑动平均模型和自回归滑动平均模型。因其具有时间相依的直观形式和较强的适用性，故水文序列的相依性一般用它们来进行描述［15］。其中，自回归滑动平均模型ARMA（Auto-Regressive Moving Average）是自回归模型AR（Auto-Regressive）和滑动平均模型MA（Moving Average）的混合，且较AR和MA能更好地反映水文变量在时序变化上的统计特性，即具有更大的弹性，在水文学中应用更为广泛［7］。国内外许多学者用其来描述水文现象在时间上的相依性。翟颢瑾等［16］使用ARMA模型模拟水质污染的相依随机过程，实现对长江未来水质情况的分析预测；栗现文和杨佳等［17-18］采用ARMA模型分析地下水位埋深时间序列中去除确定性组分之后的相依随机和纯随机组分，从而达到对未来短期地下水位动态进行准确预测的目的；Dwivedi等［19］运用ARMA等时间序列模型对降雨和径流的随机相依水文过程建模，从而实现对降雨的预测和径流量的估计；Atan 等［20］利用ARMA 模型的相依性特征模拟洪水时间序列并对流域洪灾风险进行了评估与分析等。然而，目前的研究主要是运用ARMA模型表征水文序列的相依特性，对于水文序列中相依变异强弱的量化研究则鲜有提及。赵羽西等［21］的研究虽涉及到对序列相依变异程度的分级量化，却也仅适用于AR 模型，至于其它模型尚需进一步补充和完善。此外，在运用AIC、BIC 等定阶准则对含有AR⁃MA相依成分的水文序列进行定阶时，只能确定模型的自回归阶数p与滑动平均阶数q的和（即p+q的值），而在AIC和BIC函数最小值不唯一或阶数p和q有多种组合方式时，并不能对其做出明确判断。

为此，本文以适用性更为广泛的ARMA模型为例，在已有研究［21］的基础上，以原序列与其相依成分间的相关系数为衡量标准，提出了描述水文相依变异强弱的一种方法。通过相关系数表达式的推求说明选用该指标进行变异分级的基本原理，并设计统计试验说明基本原理的合理性；以ARMA（1，1）和ARMA（1，2）模型为例，指出相关系数指标与自相关系数的联系；最后通过模拟时间序列和实测水文序列对所提方法进行验证，并结合水文序列的相依变异程度和相依成分与原序列的拟合效率系数为具有ARMA（p，q）相依成分的水文序列提供一种定阶的新思路。

2 分级原理与方法

2.1 相依变异分级原理一般情况下，在扣除确定性成分的影响之后，剩余水文序列xt中的相依成分可用自回归滑动平均模型ARMA（p，q）表示为：

式中：u为序列xt的均值；p为模型的自回归阶数；q为模型的滑动平均阶数；参数φ1，φ2，…，φp是待定系数中的自回归系数；参数θ1，θ2，…，θq是待定系数中的滑动平均系数；εt，εt-1，εt-2，…，εt-q为独立随机变量，其标准差为σε、均值为0，且与xt-1，xt-2，…，xt-q独立无关。

式（1）中的φ1(xt-1-u)+φ2(xt-2-u)+…+φp(xt-p-u)-θ1εt-1-θ2εt-2-…-θqεt-q为相依成分，用ηt表示，故xt能够表示为线性叠加的形式：

式中：ut=u+εt，其均值与标准差分别为u、σε，为水文序列中的纯随机成分，在我国水文统计分析与计算中通常认为其服从P-Ⅲ型分布［7］。

又因为ηt与ut相互独立，而xt的期望E(xt)=u、ut的期望E(ut)=u，故可得相依成分序列的期望值E(ηt)=0。

xt与ηt间的相关系数表达式为：

式中：

因此，由式（4）可得：

式中ση2与σx2分别为ηt和xt的方差，它们之间具有以下关系：

式中σu2为纯随机序列的方差，根据式（6）和式（7）可得：

将式（1）进行移项并整理得：

将式（9）两边同乘以xt-u并取数学期望得：

上式两端除以σx2后考虑到自相关系数的定义：

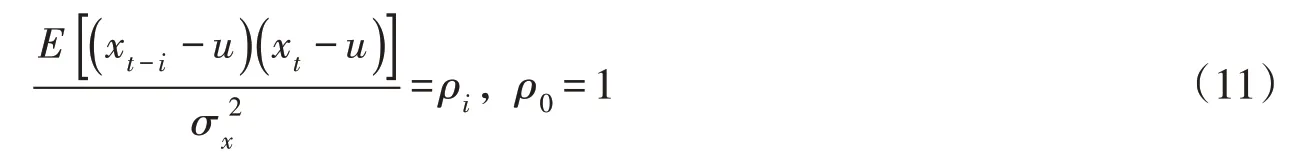
可得：

式（12）两端再同乘以σx2可得：

将式（9）两边同乘以εt并取数学期望得：

将式（9）两边同乘以εt-1并取数学期望得：

同理，依此类推，直至将式（9）两边同乘以εt-q再取数学期望得：

为此，式（13）可以化简为：

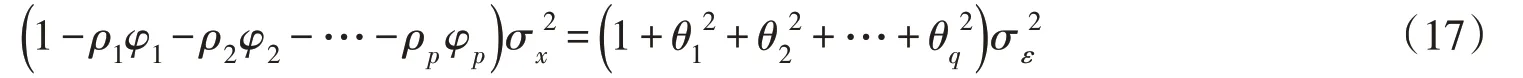
将上式进行整理得：

因为σε2=σu2，结合式（8）和（18）可得：

对式（19）进行初步验证：

当p=0时，即为滑动平均模型MA（q），式（19）可化简为：

当q=0时，即为自回归模型AR（p），式（19）可化简为：

式（20）和（21）与现有结论相符合［22］，故初步认为式（19）合理可靠。

ARMA 模型中的滑动平均系数θ1，θ2，…，θq和自回归系数φ1，φ2，…，φp的参数解与样本自相关系数存在函数关系，而样本自相关系数能够描述水文序列的相依变异程度［7］，故相关系数r能够表示样本序列的相依关系并可描述其相依程度。因此，可以用相关系数对水文序列的相依程度进行分级。

2.2 相依变异分级方法基于以上推导证明的分级原理，借鉴水文变异分级方法［21，23-25］，提出水文时间序列的相依变异分级方法。其中，选取rα、rβ、0.6和0.8作为相依变异分级界限，相应地把相关系数r分为5段区间，对应描述不同强弱的相依变异程度，具体分级标准见表1。rα和rβ分别是在已知模型阶数和序列长度的情况下，显著性水平为α和β（α>β）下的分级阈值，通常取α=0.05，β=0.01。

表1 相依变异程度分级

以ARMA（p，q）为例，利用所提方法对水文序列的相依变异程度量化分级的详细步骤如下：

（1）去除水文序列中的确定性成分，得到含有独立随机或相依成分的剩余序列xt。

（2）判断xt中是否存在相依成分。画出自相关与偏相关系数图，如果自相关系数均在容许限以内，认为剩余序列为纯随机成分；否则，认为剩余序列含有相依成分，且当自相关与偏相关系数均拖尾时，认为相依成分符合ARMA（p，q）模型。

（3）确定模型的阶数。不同于AR（p）与MA（q），据自相关系数图和偏相关系数图并不能判断出ARMA（p，q）模型的阶数，故选用两种定阶准则（AIC和BIC准则）来判定其阶数p、q。

（4）估计模型参数。用矩估计法［26］对AR⁃MA（p，q）的参数φi(i=1，2，...，p)和θi(i=1，2，...，q)进行估计，由此得到相依成分序列ηt。

（5）计算相关系数r。利用式（3）求得序列xt与ηt间的r值。

（6）判定变异等级。根据得出的相关系数r值对照表1找到对应的等级区间，由此判定出水文序列相依变异程度的强弱。

3 分级方法验证

3.1 分级原理合理性验证为验证水文相依变异分级方法对ARMA（p，q）的适用性，而实际中基于时间序列模型的水文序列预测与延展工作通常以低阶为主，故以较低阶数（p+q）的ARMA（1，1）和ARMA（1，2）模型为例，分别设计统计试验，以验证分级原理中式（19）推导过程的合理性。

3.1.1ARMA（1，1）模型ARMA（1，1）模型可以表示为xt=φ1(xt-1-u)-θ1εt-1+ut，据式（19）可得：

用Yule-Walker方程估计自回归系数φi(i=1，2，…，p)［27］：

由Yule-Walker方程可得ρ1=φ1，将其代入式（22）得到：

为满足平稳性和可逆性，各系数需符合：

统计试验详细步骤如下：

（1）利用P-Ⅲ型分布生成长为n=1000、均值u=100、变差系数Cvu=0.2、偏态系数Csu=0.4 的序列ut，然后随机生成20组自回归系数φ1值和滑动平均系数θ1值，代入式（1）得到20个ARMA（1，1）序列xi（i=1，2，3，…，20）；

（2）相依成分ηi由所得ARMA（1，1）序列xi扣除ut求取；

（3）每组系数值内试验1000 次，ηij为第i组第j次统计试验得到的相依成分序列（i=1，2，…，20；j=1，2，…，1000）；

（4）依据式（3）计算得到每组原始序列与其相依成分序列的相关系数rij（i=1，2，···，20；j=1，2，…，1000），再求出每组的平均相关系数

表2 ARMA（1，1）模型中不同参数下的ra、ri 及相对误差（δ）

3.1.2ARMA（1，2）模型ARMA（1，2）模型可以表示为xt=φ1(xt-1-u)-θ1εt-1-θ2εt-2+ut，将p=1，q=2 带入式（19）得：

因为由Yule-Walker方程得到ρ1=φ1，代入式（26）得：

为满足平稳性和可逆性，各系数需符合如下条件：

ARMA（1，2）模型的统计试验步骤参照ARMA（1，1）模型，并保持参数不变。在符合式（28）要求的情况下，随机生成20个不同φ1、θ1、θ2的系数值组合，依据模型表达式得到ARMA（1，2）序列，对比统计试验得到的平均相关系数ri与由公式求出的相关系数ra，结果见表3。可以看出，20组统计试验中只有两组结果的δ值超出5%，但不足6%，且参数个数越少，相对误差δ越小，由此验证了式（19）的合理性，说明本文所提分级原理对ARMA（1，2）模型也具有适用性。

表3 ARMA（1，2）模型中不同参数下的ra、ri 及相对误差（δ）

此外，进行了针对ARMA（2，1）、ARMA（1，3）、ARMA（2，2）和ARMA（3，1）模型的统计试验，且根据统计试验结果，本文所提分级原理与方法对于其它阶数p+q等于4阶以内的ARMA模型也是合理的，限于篇幅，详细分析结果不再展开赘述。因此，本文所提的分级原理与方法对较低阶数的AR⁃MA（p，q）模型具有普适性。

3.2 相关系数与自相关系数的关系式（19）给出了r与自相关系数的关系，其成为本文所提分级方法的理论基础。为使该分级方法的合理性更具说服力，现继续探讨相关系数与自相关系数在ARMA模型中的具体联系，此处仅以ARMA（1，1）和ARMA（1，2）模型为例。

3.2.1ARMA（1，1）模型 利用统计试验法生成具有ARMA（1，1）相依成分的序列，随机序列ut服从P-Ⅲ型分布，其长度n=1000、均值u=100、变差系数Cvu=0.2、偏态系数Csu=0.4。为单独研究两种待定系数的影响，选取两组φ1、θ1值。第一组滑动平均系数θ1取固定值0.2，自回归系数分别取φ1=-0.9、-0.5和-0.2 ； 第二组自回归系数φ1取固定值0.2， 滑动平均系数分别取θ1=0.2、0.5和0.9。图1、图2为两组情况所得各阶自相关系数。

图1和图2显示， |ρ1|不仅随着 |φ1|的增大而增大，也随着 |θ1|增加而增加。而且，序列与相依成分的相关系数r也存在与 |ρ1|一致的变化趋势，即随着 |φ1|与 |θ1|的增大而增大。由此可知，对含有ARMA（1，1）相依成分的序列而言，相关系数可以刻画其相依变异程度。

图1 滑动平均系数θ1 固定时的各阶自相关系数

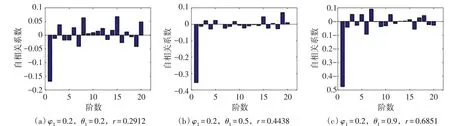
图2 自回归系数φ1固定时的各阶自相关系数

3.2.2ARMA（1，2）模型 自相关系数可以描述水文序列的相依程度［7］，在ARMA（1，2）模型中，式（27）显示r2与参数φ1、θ1、θ2有关，而滑动平均系数和自回归系数的参数解与样本自相关系数存在函数关系，所以r与自相关系数具有函数关系。根据式（28）以及自相关系数、自回归系数和滑动平均系数的关系，选取多组符合条件的ρ1、ρ2的值，并由矩估计法［26］得到ARMA（1，2）模型的参数φ1、θ1、θ2值；纯随机成分的生成同3.2.1 节。ARMA（1，2）序列减去纯随机成分得到相依成分序列。求出每种ρ1和ρ2值下的相关系数，结果如表4所示。能够看出：一阶自回归系数φ1的大小与ρ1的值无关［26，28］，且当二阶自相关系数ρ2固定不变时，相关系数r随着一阶自相关系数ρ1的增加而增加；反之，当ρ1固定时，相关系数r随着ρ2的增加而减小。说明r与 |ρ1|呈正相关关系、与 |ρ2|呈负相关关系，故对于含有ARMA（1，2）相依成分的序列，其相依性强弱也能用相关系数进行描述。

表4 不同ρ1、 ρ2 下序列的相关系数

3.3 模拟序列分析验证将所提分级方法应用于具有相依成分的模拟序列进行验证。首先从常用的显著性水平中选取第一显著性水平α=0.05、第二显著性水平β=0.01；然后根据相依变异程度分级表（即表1）中各个变异等级对应的相关系数r的取值范围，并结合所提水文相依变异分级方法的理论基础式（19），求取各相依变异程度所对应的整体变量的取值区间；最后选取满足整体变量H在取值区间内的系数值组合，生成具有相依变异成分的模拟序列。下面仍以AR⁃MA（1，1）和ARMA（1，2）模型为例进行验证。纯随机成分在模拟序列中的长度n=100、均值u=100、变差系数Cvu=0.2、偏态系数Csu=0.4，且服从P-Ⅲ型分布。

3.3.1ARMA（1，1）模型 在ARMA（1，1）模型中，它的自回归部分和滑动平均部分的阶数分别为p=1、q=1，根据式（22）—（24）可知此时整体变量H可表示为。各相依变异程度对应的整体变量H的取值区间见表5。

表5 ARMA（1，1）模型各相依变异程度区间所对应的整体变量H的取值范围

在上述条件下，分别选取一阶自回归与一阶滑动平均φ1=0.12、θ1=0.10，φ1=0.20、θ1=0.16，φ1=0.25、θ1=0.24，φ1=0.50、θ1=0.70 和φ1=0.80、θ1=0.95 共5 组系数值，由这5 组系数值求得的整体变量H分别对应相依变异程度的5个等级。模拟生成这5种情形下的序列，绘于图3，并计算出所生成序列与其相依成分之间的相关系数。

图3为相依无、弱、中、强、巨变异下模拟序列与其相依成分示意图。从图3可以直观看出，各相依成分与原序列的拟合程度依次加强，表明模拟序列的相依变异程度依次加强；求得各图的模拟序列与相依成分间的相关系数值分别为0.1556、0.2530、0.3370、0.7047、0.9004，满足表5所列出的各级相依变异程度对应的相关系数的取值区间，也从定量角度很好地验证了所提方法的合理性。

图3 ARMA（1，1）模型不同H值下相依变异分级序列

3.3.2ARMA（1，2）模型ARMA（1，2）模型的阶数为p=1、q=2，由式（26）、（27）可知整体变量H可表示为，各相依变异程度所对应的整体变量H的取值范围见表6。

表6 ARMA（1，2）模型各相依变异程度区间所对应的整体变量H的取值范围

此种条件下，分别在相依变异的5 个等级对应的整体变量H区间内各取一组满足条件的φ1、θ1、θ2组合值，同时一阶自回归系数φ1、一阶滑动平均系数θ1以及二阶滑动平均系数θ2还需满足式（28）的限制条件。选取的5 组系数值分别为φ1=0.02、θ1=0.07、θ2=0.08，φ1=0.15、θ1=0.18、θ2=0.20，φ1=0.30、θ1=0.28、θ2=0.30，φ1=0.50、θ1=-0.50、θ2=-0.40，φ1=0.80、θ1=-0.80、θ2=-0.85。所生成序列与其相依成分的示意图如图4所示，图4依次为相依变异从弱到强的5 个等级，所对应的相关系数r值分别为0.1077、0.2975、0.4703、0.6842、0.9207，均满足表6中各变异等级对应的r值区间。图4直观地显示了模拟序列相依变异的程度依次增强，而相关系数r的值也依次增加，故所提分级方法的合理性得到了验证。

图4 ARMA（1，2）模型不同H值下相依变异分级序列

4 实测序列分析

为进一步说明所提分级方法的合理性与适用性，选取实测水文序列对其进行验证，包括黄河花园口站的年径流序列（1919—2000年）、长江汉口（武汉关）站的月径流序列（2010—2015年）及长江沙市（二郎矶）站的月径流序列（1991—1998年）。按照相依变异分级方法的步骤顺序，要先扣除水文序列中的确定性成分，得到含有独立随机或相依成分的剩余序列，可以采用综合加权法［1］、滑动相关系数法［29］、Brown-Forsythe 法［30］等检测序列的跳跃点；采用分段趋势相关系数识别法［31］、过程线法、Kendall检验法［32］等鉴别趋势成分；采用滑动周期相关系数识别法［33］、周期图法、最大熵谱分析法［34-35］等检验序列的周期成分。

显著性水平分别选取α=0.05、β=0.01，对以上序列进行变异诊断分析［36］，其中结果如表7所示。结果表明，花园口站的年径流序列在1932年发生了明显的跳跃变异，这主要是气候变异直接导致的［37］；汉口站的月径流序列和沙市站的月径流序列都存在12 a 的周期变异，这种周期波动现象主要和区域的气候条件及水文地理特征密切相关［24］。

表7 实测径流序列变异诊断结果

图5为各站点实测径流去除确定性成分之后的自相关系数和偏相关系数图，蓝线为容许度为95%时的界限。由图可知，花园口站的自相关系数均在容许限以内，说明花园口站年径流序列不含有相依成分；而汉口站和沙市站序列的自相关系数和偏相关系数均呈现出拖尾的特性，表明汉口站和沙市站的月径流序列都存在相依成分，且为ARMA（p，q）相依成分。故采用ARMA（p，q）模型对汉口站和沙市站的月径流的剩余序列进行建模，ARMA（p，q）中的阶数p，q运用AIC与BIC准则进行判定：

图5 实测水文序列的自相关系数及偏相关系数

式中：n与σε2分别为序列长、残差方差。AIC准则和BIC准则类似，都是确定在有最小函数值时所对应的p和q为最佳阶数。

可得在p+q等于3和2时，汉口站和沙市站有最小的AIC与BIC值，由此可确定沙市站月径流的剩余序列符合ARMA（1，1）模型，因在ARMA（p，q）模型中q的取值一般小于p［28］，故初步判断汉口站月径流的剩余序列符合ARMA（2，1）模型，还需要根据相依成分序列与其原始水文序列的拟合效果进一步进行验证。采用ARMA（2，1）和ARMA（1，1）模型分别对汉口站和沙市站的剩余序列建模，由矩估计法［26］估计模型未知参数，并求出相关系数，具体结果如表8所示。可以看出：花园口站年径流剩余序列由AIC和BIC准则判定的阶数为1阶，但与其相依成分之间的相关系数为0.0240，比rα=0.2172小，因此该序列无相依变异，阶数也最终确定为0；汉口站序列的相关系数r=0.3418，在区间[rα，rβ]内，故其相依变异程度为弱变异；沙市站序列的相关系数r=0.4022，在区间[rβ，0.6] 内，因此其相依变异程度为中变异。

表8 实测序列相依变异强弱分级

图6为各站点实测径流序列与其相依成分的示意图。图6（b）与图6（c）为分别使用ARMA（2，1）模型和ARMA（1，2）模型对汉口站月径流序列进行拟合得到的原始水文序列及其相依成分示意图，其中ARMA（2，1）模型的相关系数为0.3418、ARMA（1，2）模型的相关系数为0.3343，从相关系数的大小初步判断ARMA（2，1）模型优于ARMA（1，2）。进一步引入一个能够验证水文模型模拟结果优劣的评价指标即纳什效率系数（NSE）［38］，其表达式为：

图6 各站点原始水文序列及其相依成分示意

式中：T为序列长度；Q0t为实测序列的第t个值；Qmt为模拟序列的第t个值；表示实测序列的均值。E的取值范围为(-∞，1]，E越接近1表示拟合效果越好，模型可信度越高；E接近0，表示模拟结果总体可信，但拟合过程存在一定的误差；E远小于0，则模型是不可信的。经计算，使用AR⁃MA（2，1）模型和ARMA（1，2）模型对汉口站月径流序列进行拟合所得的纳什效率系数分别为E1=-0.6104 和E2=-41.5755，考虑到汉口站序列的相依变异程度为弱变异，而相依变异程度越高，拟合效果越好，即拟合误差越小，所以汉口站的相依成分序列与原序列间的拟合效果相比于相依中、强、巨变异要差，此为拟合过程存在误差的原因，从而使用ARMA（2，1）模型对汉口站月径流序列进行拟合所得的纳什效率系数为E1=-0.6104 得到了很好的解释。故根据拟合效果与汉口站月径流序列的相依变异程度可以判定汉口站月径流的剩余序列符合ARMA（2，1）模型，这为AIC和BIC函数最小值不唯一或阶数p和q有多种组合方式时，提供了一种对ARMA（p，q）相依成分进行定阶的新思路。图6直观地显示，实测径流序列与其相依成分的拟合程度逐渐加强，说明实测序列的相依变异等级越来越高，故该分级方法的适用性在实测水文序列的应用中得到了验证。

受自然和人为等因素的影响，水文要素常常呈现出一定的相依特性，故从气候和人为两方面对各站径流序列的相依变异做出物理成因分析［21］。花园口站位于黄河下游，它的年径流序列无相依变异主要是其总体受气候变化与人类活动的影响较小［23］；相较于气候变化，人类活动对长江中游径流变化的影响更加显著［39］，沙市水文站地处湖北省荆州市，作为长江中游荆江河段的关键控制站，它上游葛洲坝和三峡水利枢纽的运行和建设是导致此站月径流中变异的重要原因，其次还受到沿程护岸工程以及洲滩守护工程的影响［40-41］；汉口站地处湖北武汉，是对汉江入汇长江后的水情进行控制和监测的重要站点，虽然受到长江上游水利工程的影响，但汉江的水利工程设施相对较少，汇入长江后，水文相依变异程度减轻为弱变异［13］。

5 结论

为定量研究水文序列中相依性的强弱，本文提出了一种基于自回归滑动平均模型（ARMA）的水文序列相依变异分级方法，分析验证后得出结论如下：

（1）由分级原理可知，ARMA模型中的自回归系数和滑动平均系数的大小影响着相依成分与水文时间序列间相关系数r的取值，而滑动平均系数和自回归系数的参数解与样本自相关系数存在函数关系，基于此建立了相关系数r与能够表征水文序列相依程度的样本自相关系数之间的联系，即相关系数r可以表示样本序列的相依关系并描述其相依程度。此外，本文所推导的相关系数r与ARMA（p，q）模型参数间的关系（即式（19））在以往的文献中并未提及，该关系可为后续对自回归滑动平均模型与相关系数的研究提供参考。

（2）运用统计试验证明了分级原理与方法对较低阶数的ARMA模型的合理性。①公式计算和统计试验所得r值差别很小，证明了式（19）的合理性；②在ARMA（1，1）模型中，相关系数r和自相关系数|ρ1|均随自回归系数的绝对值 |φ1|和滑动平均系数的绝对值 |θ1|的增大而增大；在ARMA（1，2）模型中，r与 |ρ1|呈正相关关系、与 |ρ2|呈负相关关系，说明以相关系数作为指标衡量序列的相依性强弱是合理的；③根据整体变量H的取值范围，生成模拟水文序列，所得相关系数处于对应变异程度的取值区间，进一步说明此方法合理可靠；④而本文所提的分级原理与方法对于更高阶数的ARMA（p，q）模型是否适用尚需进一步研究与探讨。

（3）实测序列分析表明：黄河花园口站年径流序列无相依变异、长江汉口（武汉关）站月径流序列为相依弱变异、长江沙市（二郎矶）站月径流序列为中等程度的相依变异。并结合物理成因从气候变化和人类活动两个方面很好地解释了各站点实测水文序列相依性依次加强的原因，验证了所提分级方法的合理性及对实测水文资料的适用性。

（4）提供了一种具有ARMA（p，q）相依成分的水文序列定阶的新思路：在AIC和BIC函数最小值不唯一或阶数p和q有多种组合方式时，可以先根据原始水文序列的相依变异程度初步判定模型阶数是否合适，再根据其与相依成分的拟合效率系数最终确定模型阶数。