基于输水损失动态变化特性的渠系优化配水模型研究

廖相成，胡铁松

（武汉大学水资源与水电工程科学国家重点实验室，湖北武汉 430072）

1 研究背景

渠系输配水计划编制的主要任务是在渠系物理特性固定条件下，依据未来农业气象条件和灌溉可利用水量变化合理确定灌区各级渠道引水量大小、持续时间和引水频次。因此，输配水直接关系到灌溉服务质量，输配水多了会导致灌区水资源浪费、地下水位上升和盐碱化等问题；反之，输配水少了则导致干旱缺水和作物减产。我国大型灌区骨干渠系水利用系数在2015年才达到0.597［1］，大量的水资源在渠系输配水过程中因渗漏损失浪费掉了。从这个角度讲，如何进行渠系优化配水以减少渠系渗漏损失，对于我国节水型社会建设以及最严格水资源管理具有重要的意义。

目前渠系优化配水研究主要聚焦在渠系优化配水模型构建和模型求解算法上［2］，并呈现出以下特点：对田间渠系配水的研究多于对骨干渠系配水的研究，对具体某一级渠系配水的研究多于对整体灌溉渠系配水的研究［3］，对求解算法的研究多于对模型构建的研究［4］（如模型目标中渗漏量最小是否合适与全面），尤其是等流量和不等流量条件下采用0-1规划进行田间渠系轮灌优化配水编组的研究较多［5-10］。渗漏损失最小化是渠系优化配水在模型构建方面研究的主要目标之一［6，8，11］，但目前各种优化配水模型中对渗漏损失特征的描述和准确量化研究还存在明显不足。渠系优化配水是根据不同渠道控制区域内的种植结构、作物需水量和土壤质地的时空差异性来合理调配各级渠道适宜引水过程以实现渗漏损失最小化的目标。从这个意义上讲，准确量化输配水过程渗漏损失是能否实现这一目标的关键，也是优化配水的主要挑战之一。部分学者［12］采用简单的打折法确定输配水渗漏损失，Mishra等［13］在印度普尔纳哈拉分干渠输配水研究中假设农渠和斗渠分别按照20%和15%计算；部分学者如Delgoda 等［14］、Liu 等［15］、Guo 等［16］等假设渠道中的水流始终处于稳态，将渠道每公里输水损失看成一个常数，或者假定渠床土壤透水系数和指数具有时不变特征，不随配水时间进程变化，采用如考斯加科夫（Kostiakov）公式等经验公式法计算渗漏损失［17-20］。然而在实际的渠道输配水过程中，土壤透水能力以及流量、流速等水力因素都是显著改变的，这导致渗漏损失具有明显的随时间、随流程动态变化的特征。忽视这些特征将导致渗漏损失被严重高估或低估，与实测结果相比，Shah等［21］和Zhang等［22］发现考斯加科夫公式的计算值高估了1.5倍和2.5倍，Akkuzu［23］发现莫里兹（Moritz）公式和戴维斯-威尔逊（Davis-Wilson）公式估算的渗漏损失远低于实测值。

土壤水分入渗是水分在土壤水势梯度的作用下通过土壤孔隙进入土壤并在其中运动的过程。Mishra 等［13］认为除受渠床土壤性质、渠道断面形式与衬砌状况、渠道水深等水力特性以及地下水埋深等多种因素的影响之外，渠床土壤湿润状况是渠床土壤入渗速度的重要制约因素；另一方面，渠床土壤湿润状况也受到渠道渗漏、地下水补给等因素的影响，是一个动态变化的量，从水量平衡来看，渠道输配水过程中渠床土壤当前阶段的湿润状况只与前一阶段的湿润状况以及前一阶段的地下水埋深、流量等因素有关，而当前阶段的湿润状况一旦确定，渠床土壤湿润状况未来阶段的发展不再受当前阶段以前各阶段状况的影响，即渠床土壤湿润状况具有无后效性。渠床土壤湿润状况的动态变化及无后效性特征对渠床土壤入渗具有重要影响，但目前渠系优化配水渗漏计算经验公式法并没有考虑这些特征，而是将相关的模型参数处理为常数，故而产生了较大的计算误差。因此，建立能够描述渠床湿润状况动态变化及无后效性特征的渠系优化配水模型是减少渠系渗漏损失的关键。

本文着力描述渠系渗漏损失动态衰减特征，通过对渠床湿润状况无后效性的描述，提出了渠床土壤透水系数和指数动态计算方法，在此基础上建立了一种新的考虑渠系渗漏损失动态特征的渠系优化配水模型，并在河套灌区骨干渠系优化配水中取得了良好的效果。

2 模型与方法

本文建立了一种新的考虑渠系渗漏损失动态特征的渠系优化配水模型，它包括两个模块，一个是以输水损失最小化为目标的渠系优化配水模型，一个是基于前期影响含水量的渠道输水损失动态计算模型。

2.1 基于前期影响含水量的渠道输水损失动态计算模型（DCLM）要准确计算渠道输水的渗漏损失，仅把水力参数作为变量是不够的，还必须考虑其他因素的变化。渠床土壤干湿程度直接关系其透水性能，对输配水渗漏损失有较大影响，渠床土壤湿润度越高，水分入渗锋面土水势越高，水分入渗锋面与渠床水势梯度就越小，因此土壤入渗能力越低［24-27］。渠系输配水过程初期或者是轮灌渠道，渠床土壤干燥，此时土壤入渗处于自由渗漏阶段，渠床土壤入渗速度较大；反之，若渠道行水时间较长，处于输配水过程中后期，渠床土壤已被充分湿润，渠床渗漏可能处于稳渗阶段，渠床土壤入渗速度较小。

渠床土壤含水率是准确表征其湿润程度的重要指标，但存在直接测量成本高和时空变异性大的缺陷，难以在灌区这样大尺度输配水管理中应用。借鉴水文学前期影响雨量的概念，本文探索性提出渠床土壤前期影响含水量和相对湿润度作为间接衡量渠床土壤干湿程度的指标，描述渠床土壤干湿程度在渠道输水过程中的变化，并将其与常用的计算渠道输水损失的经验公式参数结合，从而形成了既形式简便、又能考虑渠床土壤透水性变化且满足渠系输配水管理的渠道输水渗漏损失动态计算模型。

渠床土壤前期影响含水量的计算需考虑渠道输水的下渗水量补给、土壤水的蒸散发消耗及土壤蓄水容量上限，其计算公式为：

式中：Wa，t+1、Wa，t分别为第t+1 时段、第t时段的前期影响含水量，m3；Vt为第t个时段渠道的输水量，m3；K为渠床土壤蓄水的消退系数；Wam为渠床土壤蓄水容量，m3。用式（1）计算Wa时，可取渠道停水较长时间后的Wa等于零，或取渠道连续大流量运行较长时间后的Wa等于Wam，由此向后逐时段推算，便可求得渠道输水过程中各个时段的Wa。渠床土壤的干湿程度可用相对湿润度表示：

式中：θt为第t个时段渠床土壤的相对湿润度，反映了渠床土壤的透水性特征。考斯加科夫公式中渠床土壤透水系数A和指数m随渠床土壤的相对湿润度θt变化而动态变化，本文将其视为与渠床土壤相对湿润度动态有关的动态变量A(θt)和m(θt)，鉴于考斯加科夫公式在我国应用的广泛性，提出下述基于前期影响含水量的渠道输水损失动态计算方法：

式中：σ(t)为每公里渠道输水损失系数，即单位渠长的流量损失率，1/km；Qn为渠道净流量，m3/s。从式（3）可以看出，单位渠长流量损失率σ不仅与渠道净流量Qn有关系，还与渠床土壤动态透水系数A(θt)和动态指数m(θt)密切相关，而A(θt)和m(θt)是随渠床土壤相对湿润度θ的变化而变化的，是θ的函数。A(θt)和m(θt)的具体函数形式依据实际问题确定，本文简化为线性关系：

式中a、b、c、d为常数。

渠道输水损失动态计算模型中的参数K，Wam以及函数关系A(θt)、m(θt)需要结合实测的渠道输水资料进行率定，率定过程如下：首先根据渠道输水的流量数据，采用水量平衡法计算渠道输水过程中各个时段的水量损失ΔW和单位渠长流量损失率σ，计算公式见式（6）、式（7）：

式中：ΔT为输水时段时间长度，s；Q人和Q出分别为流入渠道和流出渠道的流量，m3/s；L为渠道长度，km；然后假定不同的K，Wam组合，用式（1）计算渠道输水过程中各个时段对应的前期影响含水量以及渠床土壤相对湿润度θ；再以θ为参数，点绘某一θ下的单位渠长流量损失率与渠道净流量的关系曲线，即得到渠道的σ～θ～Qn关系图；最后用式（3）对关系图中的曲线进行拟合，优选出使拟合优度最大的K、Wam，同时得到不同θ下的A与m值，采用式（4）和式（5）拟合即得到函数关系A(θt)、m(θt)。

渠道输水损失动态计算模型率定完成后，利用该模型计算渠道输水的水量损失，与采用水量平衡法计算的水量损失结果进行对比，验证模型的可靠性。模型检验的评价指标选择平均相对误差（MRE）和相关系数（R）：

式中：n为样本数；Pi为动态计算模型第i个模拟值；Oi为水量平衡法第i个计算值；Pave和Oave分别为动态计算模型模拟和水量平衡法计算的平均值。

2.2 渠系优化配水模型灌溉渠系输配水计划的编制一般要经历自上而下——自下而上——再自上而下3个编制过程［16］，即上级渠道的管理者发布整个灌溉区域的用水计划，下级灌溉子区用水户以此为基础各自制定子区用水计划，最后再由上级管理者统一协调，确定尽量满足各子区的需水要求等多个目标的计划。计划编制建模过程中通常将其概化为一个多级多水源的多目标决策问题。多级指灌溉渠系是从水源取水、输送、分配到田间的各级渠道网络，如总干渠、干渠、分干渠、支渠等骨干渠道和斗渠、农渠、毛渠等田间渠道，多水源包括河流、水库等多种水源，目标包括渗漏损失最小、产量最大等。为简化计算，本模型仅以单水源双目标的两级骨干渠道组成的渠系优化配水问题建立模型。

假设上级渠道共有M个渠段U1、U2、…、UM，连接有N条下级渠道D1、D2、…、DM，在渠段末端分水给各下级渠道再由下级渠道将水量分配到各灌溉子区C1、C2、…、CZ，配水时段总数为T，如图1所示。

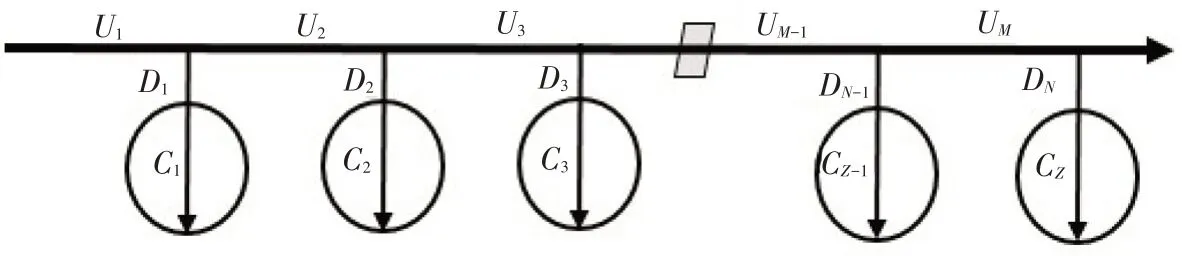
图1 灌区渠系示意（U1—UM，上级渠道渠段编号；D1—DN，下级渠道编号；C1—CZ，灌溉子区编号）

2.2.1 目标函数 模型以N条下级渠道在T个时段的渠首配水流量为决策变量，将目标函数设置为下级用水户缺水量和上级渠道输水水量损失最小，即：

式中：Wl为上级渠道输水的水量损失，m3；Ws为下级用水户各时段的缺水总量，m3；Qjtd为下级渠道Dj渠首第t时段的输水流量，m3/s；Δt为时段长度，s；Wjt为第j条下级渠道第t时段的需水量，m3；qiut为上级渠道Ui第t时段的损失流量，m3/s。

渠道流量损失分别采用考斯加科夫经验公式和上节中的动态计算模型计算，以对比分析两种优化配水结果的差异。采用考斯加科夫经验公式计算时：

式中：Aiu、miu分别为上级渠道Ui的渠床土壤透水系数和指数；Qitu为上级渠道Ui末端第t时段的输水流量，m3/s；Liu为上级渠道Ui的长度，km。

采用动态计算模型计算时：

2.2.2 约束条件

（1）渠道输水能力约束：为了保证渠道安全稳定运行，渠道输水流量不得超过设计流量。

式中：Qius、Qjds分别为上级渠道Ui、下级渠道Dj的设计流量，m3/s。

（2）灌溉可引水量约束：受来水条件限制，上级渠道渠首引水流量不得超过其最大可引流量。

式中Qtumax为上级渠道第t时段的最大可引流量，m3/s。

（3）渠段水量平衡约束：上级渠道第i渠段的末端流量应等于该渠段末端所连的各下级渠道渠首流量与上级渠道第i+1渠段渠首流量之和。

（4）非负约束：各决策变量的技术性约束。

（5）公平性约束：受到上级渠道设计流量和来水流量的限制，各下级渠道灌溉子区可能出现缺水情况。为了保证配水的公平性，需将各灌溉子区的缺水比例差值控制在合理的范围内。

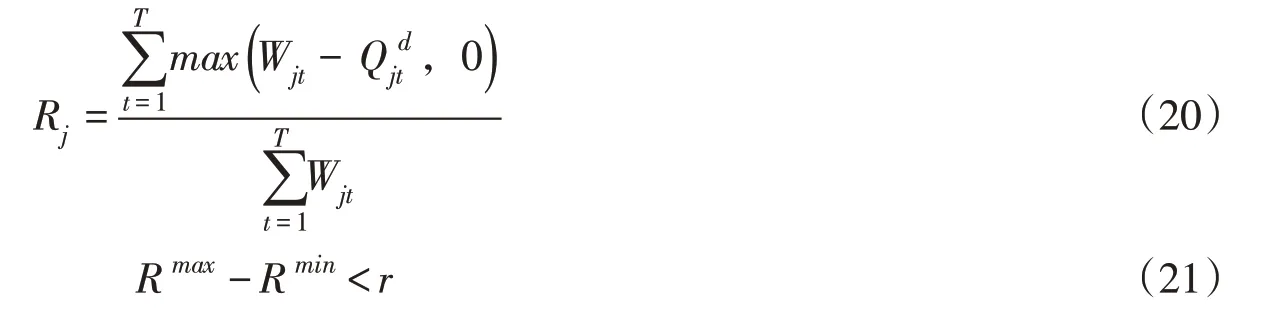
式中：Rj为第j条下级渠道所在的灌溉子区的缺水比例；R max、R min分别为各灌溉子区中的最大缺水比例、最小缺水比例；r为允许的缺水比例差值。

3 实例研究

3.1 研究区概况内蒙古自治区河套灌区的地理区域为106°20′—109°19′E、40°19′—41°18′N之间，总土地面积119 hm2，是全国特大型灌区之一，灌区自西向东分为乌兰布和、解放闸、永济、义长和乌拉特五大灌域。灌区气候干旱，属于没有灌溉便没有农业的地区［28］。总干渠是河套灌区一首制引黄灌溉的输水大动脉，位于河套平原南缘，共连接有14条干渠、9条分干渠和2条支渠，其输水运行状况对灌区渠系水的利用效率有着重大影响。为简化起见，按照所属灌域及其引水口位置，本文将总干渠上的干渠、分干渠、支渠和直口渠等多级渠道概化为7条干渠，如表1和图2所示，只研究总干渠-干渠组成的两级灌溉渠系优化配水问题。

图2 河套灌区总干渠系示意

总干渠各渠段以及各下级干渠的主要技术参数如表1所示。

表1 总干渠系渠道参数

河套灌区目前渠系输配水总干渠以续灌为主，而永济等灌域采取以轮灌为主，大轮灌、小续灌、轮续结合的方式。受地域差异大、“三秋”（秋收、秋翻、秋浇）矛盾突出等问题影响，难以做到科学合理配水和集中统一调度，存在渠系满负荷运行时间短、半渠水运行和开关口时间不一等配水流量合理控制问题，输配水效率尚待提升。从图3显示的2002—2019年总干渠输水流量概率分布来看，总干渠整体输配水流量偏小，小流量和半渠水运行的比例超过了60%，不利于渠道水利用效率的提高。

图3 总干渠2002—2019年输水流量的概率分布（流量数据为总干渠渠首2002—2019年的逐日引水流量，m3/s；设计流量为565m3/s；概率密度、累积概率分别采用MATLAB中的ksdensity函数、ecdf函数计算）

图4为总干渠2002—2019年的典型年开关闸时间变化，可以看出，总干渠开关闸时间和引水进度年际变化大。在开闸阶段，部分年份总干渠开闸后流量增加迅速，渠道很快达到大流量运行状态如2009年；相反，部分年份总干渠开闸后流量增加缓慢，渠道较长时间处于小流量运行甚至停水状态，如2003年。这种年际变化主要是由不同年份作物种植结构、气象条件、渠道可引水量等因素的差异导致的，但从渠道输配水效率来看，总干渠2003年这种输水方式易造成较大的水量损失，是需要改进的。

图4 总干渠2002—2019年典型年份的开关闸时间变化分析

3.2 动态渗漏损失模型参数率定与验证利用河套灌区总干渠及其下级渠道2002—2006年的实测输水资料对模型参数进行率定。图5为总干渠各渠段的σ～θ～Qn关系，表2给出了总干渠各渠段渠道输水损失动态计算模型率定后的参数。由图5可以看出，渠床土壤相对湿润度相同时，单位渠长流量损失率与流量呈反比关系；θ越小，对应的σ～Qn曲线位置越高，表明渠道流量相同时，渠床土壤相对湿润度越大，单位渠长流量损失率越小，这些规律都是与实践经验相符的。另外，与考斯加科夫公式的拟合结果相比，渠道输水损失动态计算模型的拟合优度普遍更大，表明该模型具有更好的拟合效果。

表2 总干渠各渠段渠道输水损失动态计算模型参数

图5 渠道的σ～θ～Qn 关系（θ，渠床土壤相对湿润度；同一颜色的点代表某一θ下单位渠长流量损失率与流量的数据分布；无k的曲线为相应颜色数据散点用动态计算模型拟合的趋势线，并给出了拟合表达式和拟合优度；标k的曲线是用考斯加科夫公式对所有数据点整体拟合而成）

采用河套灌区总干渠及其下级渠道2007—2009年实测输水资料对渠道输水损失动态计算模型和考斯加科夫公式进行验证，结果如表4所示。可以看出，动态计算模型验证的相关系数大于0.7，平均相对误差小于20%，是较为可靠的；同时，与考斯加科夫公式相比，动态计算模型验证计算的相关系数更大，平均相对误差更小，表明动态计算模型在计算渠道输水损失时更为准确。

表4 模型验证结果

3.3 不同输配水方案渗漏损失对比分析利用前文建立的渠系优化配水模型，计算求解研究区域2012年夏灌期间（4—6月）总干渠-干渠两级灌溉渠系优化配水的优化配水过程，以每5日为一个配水时段，共19个时段。根据灌区气象资料、作物种植情况计算7条概化的干渠需水过程，依据刘家峡水库下泄流量资料制定灌区可引水量过程。

将基于渠道输水损失动态计算模型（DCLM）的渠道优化配水结果与基于考斯加科夫公式（Kostia⁃kov）的渠道配水结果进行对比，两种渠系优化配水方式下总干渠各渠段的水量损失情况见表5。

由表5可知，在总干渠夏灌期间的渠首引水量皆为15.552亿m3的条件下，与基于Kostiakov 公式的渠系优化配水模型相比，基于DCLM 模型配水方案显著地减少了各个渠段的渗漏损失，渗漏水量损失减少达1560万m3，渠道水利用效率由0.919提高到0.929，特别是总干渠三闸以下渠段。

表5 总干渠各渠段输水及损失水量统计

两种渠系优化配水方式下总干渠各渠段的流量损失率变化状况如图6所示。可以看出，随着输水时间的延长，两种配水方式下各渠段的流量损失率均呈现出由初始较大值逐渐减小，最后趋于稳定的规律。然而，在4月上旬至5月上旬的渠道开闸阶段，两种配水方式对应的渠道流量损失率变化过程有显著的差异。与基于Kostiakov 公式的配水方式相比，基于DCLM 模型的配水方式中，各渠段单位渠长流量损失率的初始值更小，且更快趋于稳定水平：基于Kostiakov 公式的配水方式中，U1—U4单位渠长流量损失率的初始值分别为0.0030、0.0047、0.0130、0.0165（1/km），基于DCLM 模型的配水方式中相应初始值分别为0.0023、0.0034、0.0083、0.0139（1/km），减小幅度为16%～36%；基于Kostiakov 公式的配水方式中，U1—U4单位渠长流量损失率减小到稳定水平的日期分别为5月6日（0.00039）、5月11日（0.00065）、5月6日（0.00143）、5月16日（0.00349），基于DCLM 模型的配水方式中相应日期分别为5月1日（0.00036）、5月1日（0.00067）、5月1日（0.00143）、5月10日（0.00326），相应提前5～10日。5月上旬后，两种配水方式下各渠段的流量损失率均减小到较低水平，差异不大。

图6 总干渠单位渠长流量损失率变化对比

由表5和图6还可以看出，总干渠各渠段的渠道水利用效率差别较大，在两种优化配水模型中均呈现出从U1至U4依次降低的规律。

3.4 不同输配水方案配水进度对比分析将基于渠道输水损失动态计算模型（DCLM）的渠道配水过程与基于考斯加科夫公式（Kostiakov）的渠道配水过程进行对比，总干渠及7条概化干渠输配水流量过程分别如图7和图8所示。

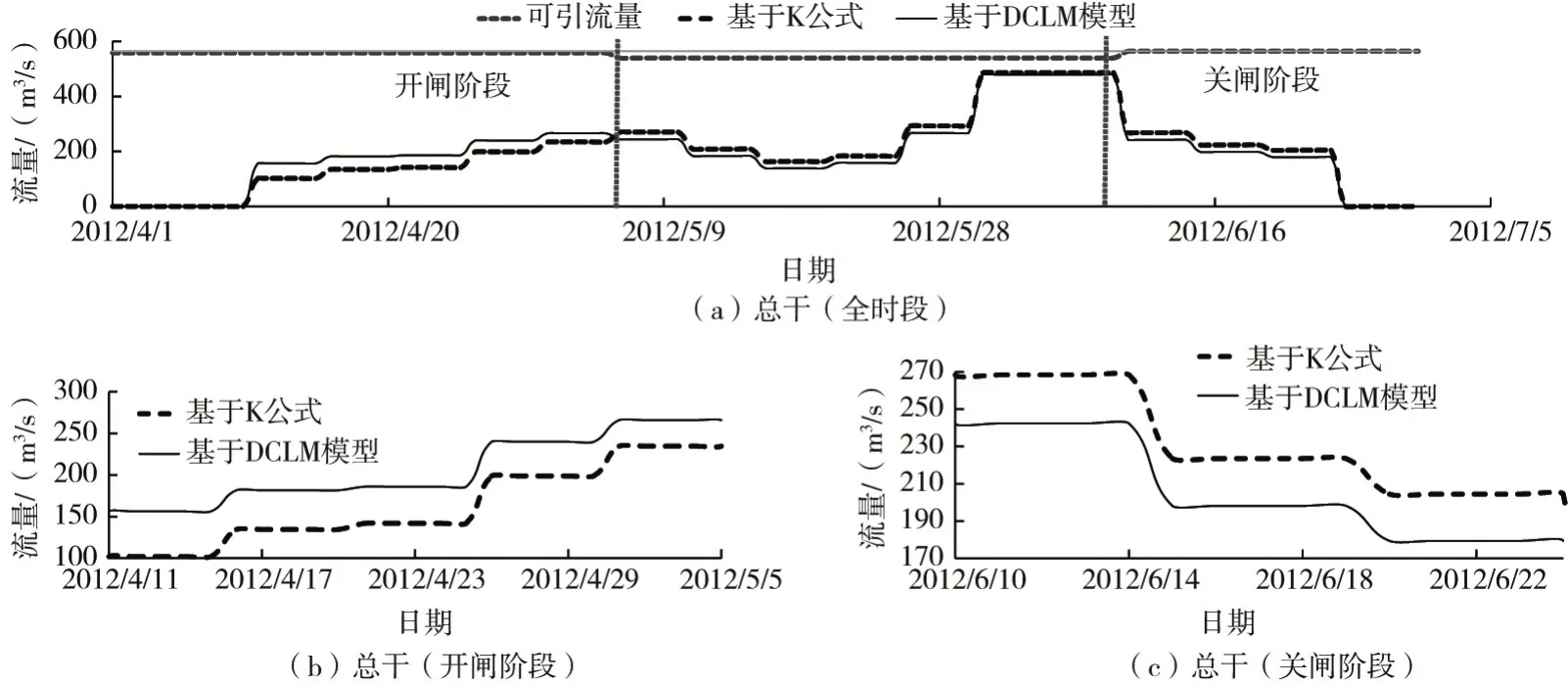
图7 两种配水方式对应的总干渠流量过程对比

图8 两种配水方式对应的干渠流量过程对比

由图7、图8可以看出，两种配水方式对应的渠道流量过程之间存在明显的差异。与基于Kostia⁃kov 公式的渠道输配水流量过程相比，基于DCLM 模型的优化配水在4月10日至5月5日的渠道开闸阶段配水的流量更大，配水中后期运行的流量更小。图7（b）中，在总干渠开闸阶段，基于DCLM模型的配水流量比基于Kostiakov 公式的配水流量大15%～55%，随着配水的进行，两种模型的配水流量差距逐渐缩小，在图7（c）显示的关闸阶段，基于Kostiakov 公式的配水流量比基于DCLM模型的配水流量普遍大10%左右。图8显示的两种配水方式下各干渠的流量过程对比也呈现出与总干渠相似的规律。产生这种区别的原因在于：DCLM模型在计算渠道的输水损失时考虑了渠床土壤干湿程度的影响，开闸阶段渠床土壤较干燥，加大流量运行有利于渠床土壤尽快达到湿润状态，为减少后续时段的损失水量打下了良好基础；配水中后期，渠床土壤已充分湿润，无需通过加大流量以减少渗漏损失，这时减少缺水量是配水调度的主要目标。

两种优化模型在渠道流量过程方面的差异导致了渠床土壤干湿程度变化情况亦有较大不同。如图9所示，基于考斯加科夫公式的配水方式，在渠道输水初期行水流量较小，导致渠床土壤湿润较为缓慢，U1—U4的渠床土壤达到完全湿润状态的日期分别为5月6日、5月16日、5月11日、5月16日；基于DCLM 模型的配水方式，在渠道输水初期加大流量运行，使得渠床土壤湿润更为迅速，U1—U4的渠床土壤达到完全湿润状态的日期分别为5月1日、5月1日、5月1日、5月11日，相应提前了5～15日。

综合图9中渠床土壤干湿程度的变化情况以及图6中单位渠长流量损失率的变化过程，可将渠道渗漏损失随输配水时间的变化过程划分为初渗和稳渗两个阶段：初渗阶段，渠床土壤由干燥状态逐渐湿润，渠道单位渠长流量损失率由初始较大值逐渐减小；稳渗阶段，渠床土壤已达到完全湿润状态，渠道单位渠长流量损失率趋于稳定较低水平。在渠道初渗阶段适当加大流量运行，可使渠道更快进入稳渗阶段，减小渠道输配水过程中的渗漏水量损失。

图9 总干渠渠床土壤相对湿润度变化对比

4 结论

本文通过引入渠床土壤前期影响含水量概念来描述渠床土壤湿润程度动态变化，建立渠床土壤透水性参数与相对湿润度之间的函数关系，在此基础上提出了一种新的考虑渠系渗漏损失动态特征的渠系优化配水模型。与考斯加科夫公式等经验公式相比，该模型能够反映渠床土壤透水性在渠道输水过程中的动态变化，对渠道输水损失机理的描述更加科学准确，配水过程更为合理。在河套灌区总干渠系的夏灌输配水实例研究中发现：与基于Kostiakov公式的配水方式相比，基于动态计算模型的渠系优化配水方式在渠道输水初期加大了15%～55%的配水流量，使渠道更快地由初渗阶段进入到稳渗阶段，渠床土壤达到完全湿润状态和单位渠长流量损失率减小到稳定水平的日期分别提前了5～15日、5～10日，从而在不增加总干渠引水量的情况下减少渠道渗漏损失水量1560万m3，将渠道水利用效率提高1%。

本文提出的渠系优化配水模型可为灌区制定合理的渠系输配水计划提供决策依据，以达到减少渗漏损失、提高渠道水利用效率的目的。但该模型对渠道渗漏损失动态变化特性的机理描述还不够全面，仅考虑了渠床土壤透水性和渠道流量在时间上的动态变化，未能反映这些因素沿渠道流程变化对渗漏损失的影响。进一步的研究将围绕这方面展开，以期更加全面准确地描述渠道输水损失机理。