基于“设计标准”的大型渡槽动力计算与隔减震研究

张多新，李嘉豪，王清云，王志强，崔越越

（1.华北水利水电大学土木与交通学院，河南郑州 450011；2.水利部水利水电规划设计总院，北京 100120）

1 研究背景

近10年内，大型渡槽的研究工作卓尔不凡［1］，标志性的成果是渡槽抗震计算与设计的相关条文被列入《水电工程水工建筑物抗震设计规范》（NB35047-2015）和《水工建筑物抗震设计标准》（GB51247-2018）（以下简称“设计标准”），结束了我国渡槽抗震设计无规范可依的历史。其中，在“设计标准”中规定［2］：“对于1级渡槽，应建立考虑相邻结构和边界条件影响的三维空间模型，采用动力法进行抗震计算。”这就要求合理的处理槽体与水体的动力相互作用、科学的建立计算模型、合理的选用和输入地震波，以及建立动力响应计算方法。同时，“设计标准”中还规定［2］：“对于设计烈度为Ⅶ度及Ⅶ度以上的渡槽，宜在槽体与槽墩间设置满足承载力要求的铅芯橡胶支座、球型抗震阻尼支座或抗震型盆式支座等减、隔震装置。”这就要求在渡槽结构抗震计算时，要对减隔震装置进行科学合理的建模，以揭示其减隔震机理及效果。

已有的研究中，限于软硬件条件，大部分成果采用了单跨或典型跨段的模型来计算大型渡槽的动力学特性和响应［3］，这类计算模型虽处理了相邻结构的影响，但处理的方法集中在对相邻跨段的质量处理，没有考虑到动力学因素的影响。同时，在槽体与水体的动力相互作用的考虑中，多采用附加质量模型［4］、弹簧-质量模型［5-6］、ALE 模型［7］、位移-压力模型［8］、流体固体接触界面的无限点对模式［9］等来简化水体与槽体的动力相互作用，这与地震作用下，槽体与水体真实的动力相互作用相差甚远［10］。在地震波的选用与激励方式上，已有研究集中在横向激励上，一般是在渡槽横向施加地震加速度进行渡槽的动力学分析，这与“设计标准”的规定相距甚远。

在大型渡槽采用隔震减震装置方面，张俊发等［11］将普通叠层橡胶支座（RB：Laminated Rubber Bearing）视为线性弹簧单元，将叠层橡胶聚四氟乙稀滑板支座（TRB：Teflon Laminated Rubber Bearing）视为弹簧-摩擦单元，开展了渡槽的地震响应分析。王博等［12］采用Wen微分型滞回恢复力模型与双线性滞回恢复力模型，建立了铅芯橡胶支座（LRB：Lead Laminated Rubber Bearing）隔震层的力学性能关系式，从渡槽槽体和墩体的位移与加速度反应结果，证明了LRB显著的隔震效果。张艳红等［13］采用双线性滞回模型模拟有阻尼隔震支座，给出8度地震作用下，渡槽顺、横槽向等效阻尼比以及隔震支座最大顺、横槽向位移。刘云贺等［14］通过非线性分析，探讨了LRB的非线性特性，深化了对LRB本质的认识。徐建国等［15］分别利用双线性模型和Wen模型来模拟LRB的非线性滞回恢复力特性，证明两种计算模型均可以较好地反映LRB的本构关系。杨世浩等［16］采用双线性模型模拟了球形减震支座（SDB：Spherical Damping Bearing），结果表明SDB具有明显的耗能效果。季日臣等［17］采用双线性滞回模型模拟了摩擦摆式支座（FPB：Friction Pendulum Bearing），证明FPB应用于大型梁式渡槽，其减隔震性能明显优于RB。黄亮等［18］采用spencer 模型模拟了磁流变阻尼器（MRD：Magneto Rheological Damper）的力学性能，表明MRD 可有效地抑制渡槽结构在地震激励下的响应，为半主动控制应用于渡槽结构的抗震设计提供了依据。郑明燕等［19］采用智能隔震结构（隔震支座和磁流变智能阻尼器构成），实现了减小地震响应和槽身侧移的目的。上述研究表明，各类隔减震装置已逐步应用于大型渡槽的抗震中，为更为清晰的理解各类装置的隔减震机理和效果，更有必要以“设计标准”为圭臬，开展大型渡槽动力学计算与隔减震研究。

本研究正在这样的背景下，以某高烈度区待建8跨大型渡槽为研究对象，把高阻尼橡胶支座应用到渡槽结构的隔减震体系中，考虑了槽内水体与渡槽的动力相互作用，建立了大型渡槽槽体-水体-支座-槽墩-基础等结构体系的动力有限元模型。同时，采用可调节阻尼的等效双线性恢复力模型对高阻尼支座进行模拟，利用傅氏逆变换拟合了符合场地特性的3套人工地震波并验证了其合理性，改进了Wilson-θ法并对渡槽体系进行了动力学求解，给出了大型渡槽的动力学响应分析和高阻尼支座的隔减震效果分析，并结合大型渡槽结构体系的动力特性和反应谱特征，分析高阻尼支座的隔减震机理，以期促进待建和已建渡槽工程的实践。

2 模型构建

2.1 槽内水体与槽体的动力相互作用模型大型渡槽的动力学问题实属流固耦合（FSI：Fluid Solid Interaction）系统的动力学问题，解析这一问题的核心在于正确认识水体与槽体的相互作用。由于渡槽的最大水深H和槽体半宽度l的比值H/l一般在1～2 之间，若忽略水体压缩性，在地震作用下，槽内水体与槽体的动力相互作用可以通过附加质量考虑，但附加质量只能表达由地震加速度引起的与其方向相同的动水压力，这也正是Westguarrd 模型［4］和Housner 模型［5-6］的缺陷。大型渡槽FSI系统正确的物理机制是：水平向地震动加速度引起的槽内动水压力，不仅是渡槽侧壁迎水面上水平向附加质量与水平向地震加速度乘积所表示的水平向动水压力，而且还会引起槽底迎水面的竖向动水压力；同样，竖向地震动加速度引起的槽内动水压力，不仅是槽底迎水面上的竖向附加质量与竖向地震动加速度的乘积所表达的竖向动水压力，而且还会引起槽壁迎水面上的水平向动水压力。故在考虑槽内水体的动水压力时，必须同时考虑地震加速度方向的动水压力分量和垂直于地震加速度方向的动水压力分量。这种复杂的槽内水体与槽体的FSI 动力相互作用，导致大型渡槽抗震计算十分复杂。基于工程实用的观点，“设计标准”中提出了渡槽槽体内动水压力的计算模型，详见“设计标准”。

大型渡槽抗震计算，应同时考虑水平向和竖向地震动分量作用，计算模型应包括支墩、槽体在内的整个渡槽结构变形体系与槽内水体的FSI作用。槽内水体的动水压力应同时考虑受渡槽结构激励处水体惯性引起的冲击动水压力和水体自身晃动导致的对流动水压力。水体可作为不可压缩流体，其冲击动水压力以固定于槽体迎水面上、沿地震动分量作用方向的附加质量体现，但同时要考虑与地震动分量方向正交的槽体迎水面上的动水压力。

2.2 高阻尼橡胶支座恢复力计算模型大型渡槽中设置的减、隔震装置，主要有RB、LRB、FPB、SDB等支座及MRD阻尼器和智能隔震结构。本文选取HDR（I）-d970×369-G1.2型支座［20］为隔减震支座，该支座的支座参数如表1所示，双线性恢复力模型如图1所示。采用可调节阻尼的弹簧单元对该支座进行模拟，每个支座采用3个弹簧模拟，竖向弹簧采用线性模型，两个水平向弹簧采用双线性模型。

表1 高阻尼橡胶隔震支座参数

图1 支座的等效双线性恢复力模型

3 地震波的选取与输入

本研究对象，场地基本烈度为8 度，采用基准期（50年）内超越概率10%的地震动峰值加速度为设计地震动峰值加速度，设计地震水平峰值加速度0.2g，特征周期0.45 s，阻尼比取0.05。依据“设计标准”推荐的设计反应谱［2］，采用逆FFT算法和Jennings包络线函数，人工拟合出符合场地特性的3套人工地震动加速度时程（如图2），作为大型渡槽的激励进行输入。

图2 人工合成地震动加速度时程特性

在图2中，每套人工地震波均给出了加速度时程、人工模拟加速度反应谱与设计反应谱曲线之间的对比、人工合成加速度时程的Fourier 谱以及功率谱。分析3套人工模拟地震加速度时程的Fourier谱，可以看出各套人工地震动加速度的低频分量较少而高频分量密集；分析3套人工模拟地震加速度时程的功率谱，可以看出第1套人工地震动低频分量的功率最大，第3套人工地震动低频分量的功率次之，第2套人工地震动低频分量的功率最小，3套人工地震动高频分量的功率相差不多。分析各套人工模拟地震加速度反应谱与设计反应谱曲线之间的对比图，可看出，3套人工地震动加速度时程均符合“抗震标准”的要求。

4 非线性地震动力方程及其求解

渡槽结构槽体-水体-减震支座-槽墩基础结构体系的地震动力反应方程是［21］：

式中：M、C、K分别为槽体的质量矩阵、阻尼矩阵和刚度矩阵，考虑到减震支座的非线性，C、K是时变的；、Dαβ、Cαβ、Gαβ分别对应流体域对流、损耗、压力和连续矩阵［22］，Ff、Fs分别为流体与固体结点外力向量；ατ为接触面已知内力向量；H为流体边界速度向量；[Cij]为流固动力耦合接触约束矩阵，可考虑接触无滑移状态和接触有滑移状态。对式（1）对称化处理并采用分时段增量法求解，可得增量方程：

式中：Cij为对称化后的接触约束矩阵；{ΔGf}、{ΔGs}为对称化后的荷载列向量。

根据Wilson-θ法基本假定，可得[t，t+θΔt]时步内任意时刻t+τ时刻加速度反应为：

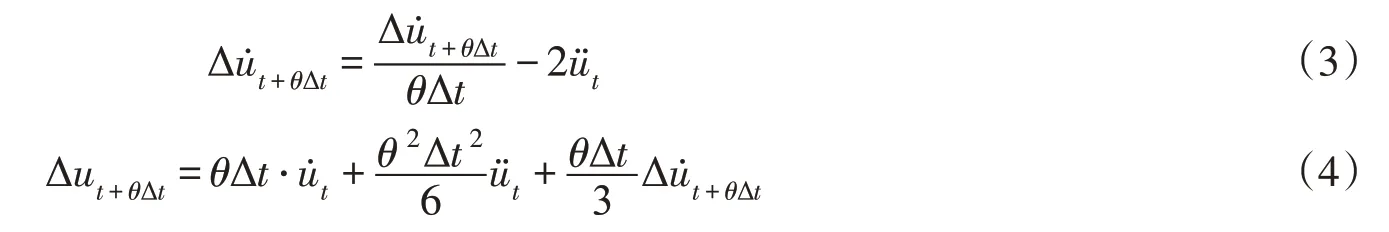
将式（3）、式（4）代入式（2）中，可得等效静力方程为：

由式（5）求得t+θΔt时刻的增量值，再由下式求得t+Δt时刻的加速度、速度、位移（对流体无意义）及压力、接触内力增量：

式（5）为隐式方程，应进行迭代求解。

5 工程实例及分析

5.1 工程背景某大型跨越河谷渡槽，设计流量120 m3/s，渡槽槽身是三箱一联的简支预应力C50混凝土结构，共计8跨，每跨30 m，全长240 m。断面净尺寸3 m～5.0 m×4.2 m（宽×高）；边墙及中墙厚0.6 m，底板厚0.5 m，拉杆尺寸为0.3 m×0.4 m（宽×高），间距2.5 m，底肋断面尺寸为0.5 m×0.9 m（宽×高），间距2.5 m。渡槽共布置7个中墩、2个边墩。槽墩采用C25钢筋混凝土实心墩，高度为6.4 m～8.4 m，中墩最大截面尺寸19.44 m×4.34 m（长×宽），墩帽平面尺寸19.8 m×4.7 m（长×宽），高2 m。柱墩基础采用C25钢筋混凝土，基础平面尺寸23.54 m×8.44 m（长×宽），高2 m。

研究建立了全段8跨渡槽的三维有限元模型，槽体、槽墩及地基土体采用三维实体单元来模拟，支座采用板壳单元-刚体单元-弹簧单元的组合来模拟，槽间止水采用三维块体单元模拟。按照取土层的长深比大于12的研究成果［23］，本文拟取土体深度为35 m，横向宽度为423 m，纵向长度为406 m，有限元模型如图3所示。采用图2所示的人工地震动加速度，并将其输入到场地底部的基岩面，横向地震动输入系数为1，竖向输入系数为2/3。

图3 有限元计算模型

5.2 计算分析研究取完建工况（空槽）和运行工况（设计水深）两个工况，分别对装有隔减震支座（高阻尼橡胶支座）和装有普通支座（普通盆式橡胶支座，其两个水平向刚度为2.72×108N/mm，竖向刚度为6×108N/mm）两种情况的大型渡槽进行了动力特性分析和响应分析。

5.2.1 动力特性分析 采用上述计算模型，利用Block Lanczos method 对渡槽结构的固有频率和振型进行提取，得到各阶自振频率及主振型。表2给了大型渡槽在完建工况时（考虑到运行工况，槽内水体会进一步影响渡槽结构体系的振动特性，故在渡槽结构动力特性分析时取完建工况来阐释高阻尼支座的隔减震效果及机理），装有隔减震支座和装有普通支座两种情况下的前10阶自振频率与周期；因一般情况支座阻尼对振型的影响不大，故图4给出了大型渡槽完建工况时的前4阶主振型。

图4 渡槽结构体系的前4阶主振型

分析表2所示内容，得出大型渡槽在设置隔减震支座之后，支座的柔性降低了渡槽结构体系的刚度，使渡槽结构的自振频率大幅降低，前10阶的最大降幅约为73%，这延长了结构的自振周期，前10阶自振周期的最大延长约为2.76倍，这成功的避开地震能量集中的范围，降低了渡槽结构的地震响应，这种“降刚增柔”的技术方法，显示出了较好的隔震效果。

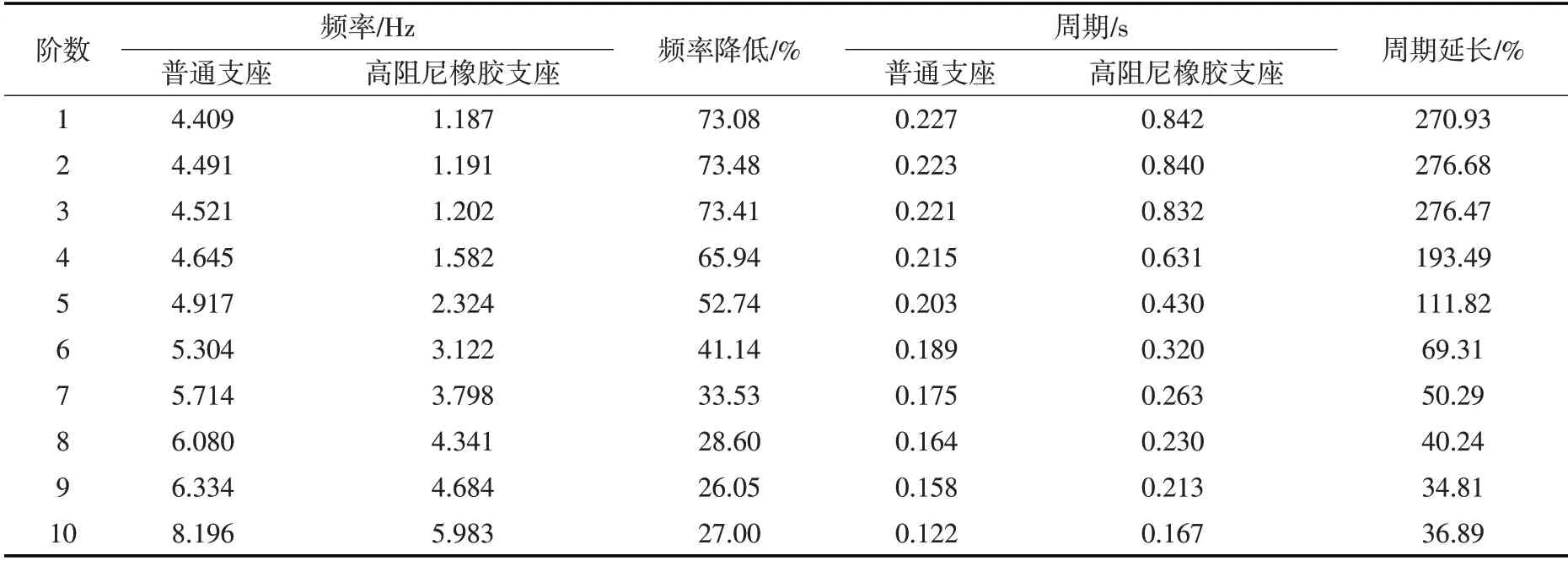
表2 渡槽结构动力特性（前10阶）

分析图4所示的主振型，可看出，渡槽结构的第1阶主振型以纵向的平移振动为主，第2阶主振型以横槽向的平移振动为主，第3阶主振型以绕渡槽纵向中断面转动振动为主，第4阶主振型和一般工程梁振动类似，以纵向弯曲振动为主，并伴随着侧向的弯曲振动。

5.2.2 动力响应分析 采用改进的Wilson-θ法，对装有隔减震支座的大型渡槽完建工况和正常运行工况的动力学响应进行了求解，地震动激励时间为20 s，峰值加速度为0.2g，给出了渡槽结构体的动位移和动应力结果。为便于论述，取中跨渡槽跨中断面上的3 个特征点（如图3（b）所示）的动位移响应和动应力响应来进行分析。以槽体顶部相对于底部的横向变形（如图5所示）、特征点C处的第一主应力时程分布（如图6所示）、空槽及设计水深时全时域全场域槽身最大第一主应力图（如图7、8所示）进行动力学响应的阐释和分析。分析图5可得出，空槽时，槽体的横向相对变形在-0.25～0.30 mm之间，最大为-0.35 mm；设计水深时，槽体的横向相对变形在-0.20～0.35 mm之间，最大为0.55 mm。分析图6可得出，空槽时，槽体特征点C处的第一主应力在0.05 MPa左右，最大值为0.1 MPa；设计水深时，槽体特征点C处的第一主应力在0.10 MPa左右，最大值为0.27 MPa。

图5 A点相对于B点的横向相对变形

图6 特征点C的第一主应力时程曲线

进一步分析图5和图6，可以得出，本研究对象中，由于水体的作用，致使渡槽在正常运行时，槽体的动应力比空槽时增大2.7倍。从槽内水体的质量和槽体的质量对比来看，槽内水体约为1687 t，槽体钢筋混凝土约为5171 t，水体质量约为槽体质量的1/3。若只考虑水体的惯性力作用，运行工况的槽体的动应力应比空槽时增大1.33倍，而计算的结果是增大2.7倍。这是由于采用“设计标准”推荐的槽体动水压力计算模型，在横向和竖向，既考虑了水体的对流冲击作用，又考虑了水体的脉动压力作用，还考虑了与地震动作用方向相垂直的动水压力，计算结果合理且有利于渡槽结构的设计。

同时，还发现，在地震波作用下，正常运营情况下槽体的动位移和动应力在地震激励后期，槽体的动响应得到了进一步的放大，这是因为“设计标准”在建立槽体动水压力时，采用的假定条件是水体无黏、无旋、不可压缩等假定，在地震作用下，槽内水体吸收了一部分能量，在地震作用后期，水体将吸收的这一部分能量释放出来的结果，这应引起工程界的足够重视。

为了适应水工混凝土结构设计承载能力极限状态计算和正常使用极限状态验算的表达式，需要将地震作用的响应按分项系数的原则，叠加到设计表达式中。而在时程分析中，每一步计算就有一个响应结果，叠加哪一步的计算结果，就值得探讨。考虑到1 级大型渡槽是调水工程的关键性建筑物，应将地震作用下最不利的状态叠加到设计表达式中，这就需要找出全激励时间内，特定（设计）跨渡槽全槽身某一响应的最大值，称之为全时域全场域的最值。

为此，本文采用先时域后场域的搜寻最值的算法，找出了大型渡槽中跨槽身的第一主应力全时域全场域的最值，如图7和图8所示。分析图7和图8，可以发现在完建工况下，中跨渡槽第一主应力全时域全场域的最值为11.50 MPa，发生在第438步（8.66 s），位于支座与槽身的连接处；在正常运行工况下，中跨渡槽第一主应力全时域全场域的最值为11.10 MPa，发生在第367步（7.32 s），两种情况第一主应力的最值均发生在支座与槽身的连接处，属于应力集中。

图7 空槽时槽身全时域全场域最大第一主应力图

图8 设计水深时槽身全时域全场域最大第一主应力图

在应用水工混凝土结构设计承载能力极限状态计算和正常使用极限状态验算的表达式时，采用同样的方法，找出相应响应在全时域全场域的最值，按分项系数的原则进行叠加。

5.2.3 隔震减震分析 本节针对大型渡槽的正常运行工况，在3套人工地震动作用下，分别对装有隔减震支座和装有普通支座两种情况下的动力响应进行求解，给出了大型渡槽的动位移和动应力解答，通过两种情况的对比，来阐释支座的隔减震机理及效果。图9给出了3套人工地震动作用下槽体顶部相对于底部的横向变形，图10给出了3套人工地震动作用下隔减震支座恢复力-位移滞回曲线。

分析图9所示内容，可以得出大型渡槽在运行工况时，采用高阻尼隔减震支座，3套人工地震动作用下槽体的横向变形量相对于普通支座分别降低了61.2%、62.3%、56.6%，应力也有同样的结论；图10给出的隔减震支座恢复力-位移滞回曲线，形状饱满，说明在运行工况中，高阻尼隔减震支座耗散地震能力较为明显。

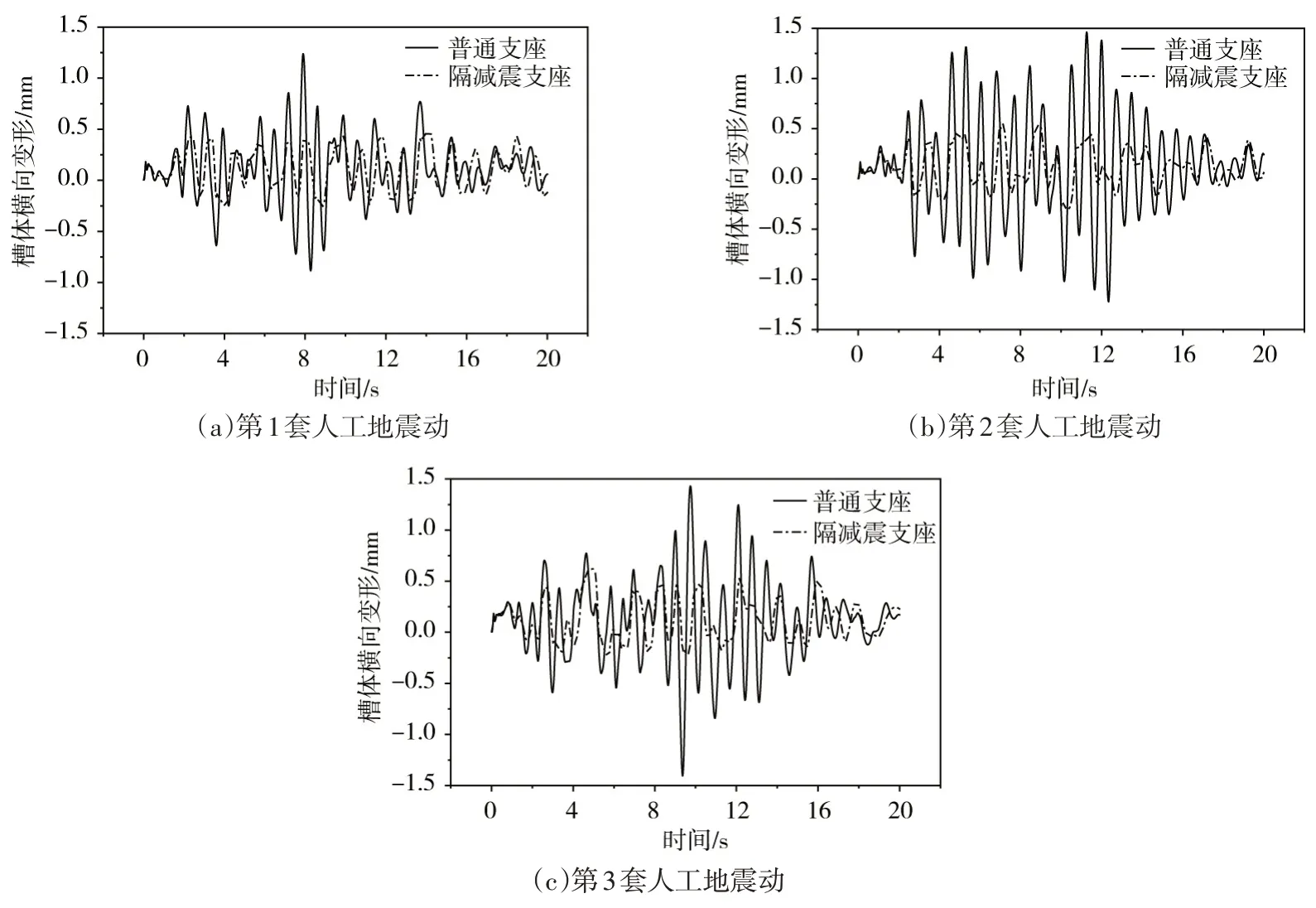
图9 A点相对于B点的横向相对变形

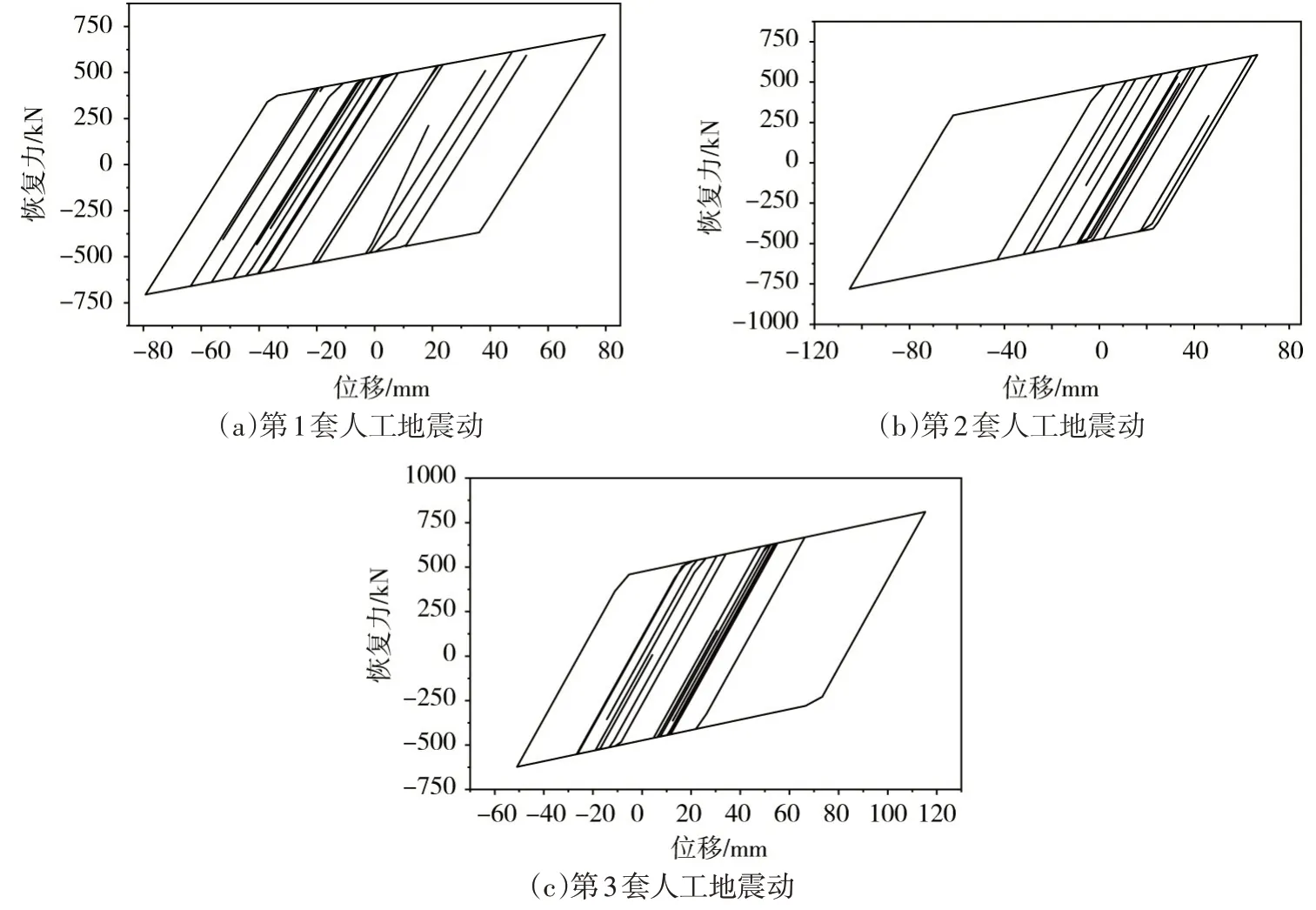
图10 隔减震支座恢复力-位移滞回曲线

分析高尼阻隔减震支座的恢复力-位移滞回曲线，可得出，在3套人工地震动加速度时程的激励下，支座的滑动位移分别约在在-80～78 mm、-105～60 mm、-50～110 mm范围之间，进一步观察渡槽结构体的主振型，可以看出，支座的滑动位移主要是由第2 阶振型（如图4（b））的“贡献”所引起。也正是支座与槽体的这种“类刚体”横向振动，致使高阻尼支座的阻尼效应充分发挥，减轻了槽体的地震响应。

综上分析，可以看出高阻尼隔减震支座的引入，显著的降低了渡槽结构体系的地震响应。这一方面是由于高阻尼隔减震支座增加了渡槽结构体系的阻尼，这种“控制增阻”的技术措施，使地震反应谱的谱值减小，即耗散了地震动输入到渡槽结构体系的能量所致。另一方面是由于高阻尼隔减震支座增加了渡槽结构体系的柔度，降低了渡槽结构体系的刚度，这种“降刚增柔”的技术措施，延长结构的自振周期，避开地震能量集中的范围，降低了渡槽结构体系的地震响应。

5.2.4 槽间相对错动位移分析 在运行工况下，渡槽槽间横向错动位移如图11所示。图11中分别给出了第1套、第2套和第3套人工地震动激励下8跨渡槽7个槽间的横向相对错动位移随激励的变化。

图11 运行工况时在3套人工地震动下的槽间相对错动位移

分析图11所示的3套人工地震动作用下渡槽槽间的横向相对错动位移变化图，可以看出，3套人工地震动激励下，渡槽槽间横向错动位移具有相似性。槽4和槽5之间横向错动位移在0附近上下波动，其余各槽以槽4和槽5之间的止水为中心，呈现出点对称的分布规律。

在第1、2、3套人工地震动激励下，槽5和槽6之间的横向错动位移最大值分别是-0.223、-0.286和0.269 mm，槽3和槽4之间的横向错动位移最大值分别是0.244、0.294和-0.290 mm，槽6和槽7之间的横向错动位移最大值分别是0.286、-0.424 和0.355 mm，槽2 和槽3 之间的横向错动位移最大值分别是0.285、0.411 和-0.366 mm，槽7 和槽8 之间的横向错动位移最大值分别是0.250、-0.372 和0.330 mm，槽1和槽2之间的横向错动位移最大值分别是0.243、0.373和-0.316 mm。

分析图11所给出的规律，清晰的看出，多跨渡槽在运行工况下，3套人工地震波激励下，横向错动位移表现出了一定的相似性，具有规律性，这与多跨渡槽的振动特性相关。由结构的动力特性分析可以看出，运行工况下的第3阶主振型（如图4（c））与槽间横向错动位移的变化趋势相似，可以说，大型多跨渡槽的槽间横向错动位移也是结构动力响应，主要由第3阶振型的“贡献”而引起。

6 结论

本文采用可调节阻尼等效双线性恢复力模型对高阻尼支座进行模拟，分别求解了大型渡槽在正常运营工况与完建工况时的动力响应，分析了高阻尼支座的隔减震效果，并结合大型渡槽结构体系的动力特性，分析高阻尼支座的隔减震机理，得到了以下结论：（1）在大型渡槽的结构体系中引入高阻尼隔减震支座，实质上是同时采用了“控制增阻”和“降刚增柔”两种技术措施，降低了渡槽结构体系的地震响应，说明高阻尼支座可以有效减轻强震对大型渡槽的破坏作用。（2）采用高阻尼橡胶支座，延长了渡槽结构的基本周期，增大了渡槽体系的阻尼，降低了槽体的地震动响应，保护了槽体。但增大了支座的侧移量，建议槽体与槽墩边挡块之间留有合理的间距，以免槽体与边挡块发生碰撞，并在槽墩边挡块与槽体之间设柔性保护，或在支座之间增设阻尼器及限位装置。（3）采用高阻尼支座的大型多跨渡槽工程，在地震作用下，虽然增大了槽体的横向位移响应，但槽间相对错动位移不大，一般的柔性止水不会发生破坏。（4）多跨渡槽槽间横向错动位移的产生，具有一定的规律性。本案例中的多跨渡槽槽间横向错动位移呈现出“中间小，两头大”的特点，故在设计渡槽槽间止水时，应在槽端部两个跨间加设一道止水。（5）多跨渡槽槽间横向错动位移的产生受渡槽结构动力特性的控制。本文中，槽间横向位移分布与渡槽结构体系的第3阶主振型相似，可以说，在3套人工地震动的激励下，渡槽结构体系的第3阶主振型对槽间横向错动位移的“贡献”最大。但地震动是随机的，也有可能激励起更高阶的振型，增大槽间横向错动位移，故在槽间止水设计时，应选用高韧高柔橡胶止水或铜止水，避免止水破坏，发生槽间漏水现象。（6）通过搜寻激励全时域渡槽全场域的响应最值，可给出渡槽结构动力学响应的最大值。考虑到1级大型渡槽的重要性，推荐在结构承载能力极限状态计算及正常使用极限状态校核时，应用分项系数的原则，叠加渡槽结构全时域全场域的最值动力响应，实现渡槽工程的运营安全。