联合采购与配送协同成本分摊方法

饶卫振，徐 丰，段忠菲

(山东科技大学 经济管理学院，山东 青岛 266590)

0 引言

联合采购是两家或两家以上需购买相同产品的企业将采购订单合并，由一方统一采购，再进行成本分摊，从而降低采购成本，获取较大折扣的活动[1]。随着供应链协同的出现，企业考虑采购端的合作博弈问题，以期降低整体成本，故联合采购一经提出便受到广泛的重视。而配送成本是联合采购情景的一个重要组成部分，目前，文献较多研究联合采购的优势与采购成本的合理成本分摊，较少考虑联合采购与配送的协同优化问题，或简单按购买货物量作为权重分摊配送成本。当企业采购的商品配送成本占总成本比率较高时(如个人护理类的护发品，冷链运输的医药产品)，如果优化联合采购与配送成本的合理分摊，企业联盟的成本分摊合理性将达到更优水平。

目前，众多学者研究发现了联合采购的优势，如汇集采购规模、共享市场、共享信息与资源[2-4]。张新鑫等[5]研究了集中采购对双寡头药物市场的影响，验证了集中采购能够降低采购成本的结论;COWAN等[6]选取了美国具有代表性的11组VPG(vaccine purchasing groups)并进行定性电话访谈，发现通过该机制购买大多数疫苗，可降低购买成本。期间有学者对联合采购联盟的影响机制进行了研究[7-9]。PINAR等[10]研究了联盟成员的需求分布情况，得出联盟成员的需求分布区间决定联合采购方案是否全局最优的结论;肖旦等[11]针对实际中广泛存在的横向竞争零售商联合采购的情形，采用合作博弈论中远视稳定性的概念，分析了不同数量折扣契约下稳定联盟的成员个数。同时，联合采购的研究主要集中在订货策略方面[12-13]。吴一帆等[14]以网络团购为背景，深入研究了商家服务质量与团购定价的协调问题。随后有学者对联合采购中的竞合博弈进行了研究[15]，ONGKUNARUK等[16]和CHEN等[17]对联合补货模型进行研究，考虑资金与运输能力限制的同时，增加了与残次品相关的约束条件。

联合采购行为能够带来一定的经济效益，同时采购成本的公平分摊问题成为关注点[18]。参与联合采购的企业成员采购量均有不同，高频次合作情况下成本的不合理分摊容易带来较大的成本差异。张云丰等[19]在二级改良品供应链中，考虑非瞬时补货下供应商进行独立采购与联合采购情况，并使用4种成本分摊模型进行分摊。当前Shapley值法与核仁解是成本分摊领域中公认合理的成本分摊方法，有学者将Shapley值法与核仁解引入联合采购情境中，以期提高采购成本的分摊合理性。谢晶晶等[20]采用Shapley值与核仁解对碳配额交易利益分配进行研究;王选飞等[21]将改进的Shapley值法应用于移动支付商业模式动态联盟利益分配研究。

随着研究维度的深入，合作不仅发生在采购行为中，因此有学者对联合采购与配送联合优化问题进行了研究[22]。CHA等[23]设计了混合遗传算法，求解一对多的联合采购与配送问题，并与启发式算法进行对比;ÇETINKAYA等[24]研究了不同的调度策略对库存补货与运输决策联合优化的影响;崔利刚等[25]基于联合采购与配送问题对RFID的投资决策进行分析;WANG等[26]研究了混合可变领域搜索算法，用于求解联合采购与配送协同问题，并证明了该算法的有效性。由上述文献可以看出，学者对考虑配送成本的联合采购行为研究较少，而在配送成本占总成本比率较大的商品中，由于参与联合采购的企业存在地理空间分布差异以及因采购量不同产生配送频次差异，容易导致配送成本不均衡，仅考虑合理分摊采购成本存在较大的不合理性。当企业联盟进行成本分摊时，考虑配送成本与物品购买成本的协同分摊能够极大地促进企业组成采购联盟。

本文考虑联合采购与配送协同优化的成本分摊模型，以配送成本占总成本比率大的商品为研究对象，对联合采购与配送协同优化的成本分摊问题进行深入研究。本文目标是改进现有联合采购的成本分摊现状，在Shapley值法分摊物品购买成本的情况下，加入配送成本部分进行协同成本分摊，以使得成本分摊达到一个更合理的状态。通过构建随机算例，利用Shapley值法与传统的权重分摊法分别对物品购买成本与配送成本进行成本分摊，计算两种方法所得结果的平均偏差，论证对配送成本占总成本比重高的商品，采用Shapley值法合理分摊配送成本部分的必要性。

1 考虑配送成本的联合采购成本分摊问题描述

本文主要研究考虑配送成本的联合采购成本分摊问题，即企业联盟采用Shapley值法分摊联合采购的物品购买成本与配送成本。主要思路是：企业组建采购联盟后，对物品购买成本与配送成本进行量化，在采用Shapley值法分摊物品购买成本的基础上，引入企业配送成本的Shapley值法分摊，并与权重法分摊配送成本进行对比，为企业联盟的成本合理分摊提供一个新思路。

1.1 考虑配送成本的联合采购问题

假设问题满足以下假设基础：

(1)供应商供货有一定的数量折扣；

(2)不考虑供应商缺货的情况。

1.2 联合采购成本分摊问题

企业形成联盟进行联合采购时，得到大联盟的物品购买成本C1(N)与配送成本C2(N)，如何将成本合理地分摊给各联盟企业是一个亟待解决的重要问题。目前的联合采购场景中，联盟企业以经典的Shapley值法对物品购买成本C1(N)进行分摊，并未考虑配送成本的分摊，或仅按货物购买量占总购买量的权重为准则进行配送成本C2(N)分摊。因企业的采购量不同，每个企业对整个大联盟的贡献不同，仅按照权重法对配送成本进行分摊具有其不合理性。因此本文考虑n个企业形成联合采购联盟时，在Shapley值法分摊物品购买成本C1(N)的基础上，使用Shapley值法替代传统权重分摊法分摊配送成本C2(N)。

Shapley值法为合作博弈领域中公认合理的成本分摊方法，其原理[27]如下：n个主体参与的合作问题中，能够形成2n-1个子联盟S，假定第j个子联盟S为Sj(1≤j≤2n-1)，则子联盟S=(S1,S2,…,S2^n-1)，第j个子联盟Sj的总成本为C(Sj)。在上述基础上，求解每个成员分摊的成本Φ(i)。Shapley值法如式(1)，式中|Sj|表示第j个子联盟Sj中的企业成员个数。

[C(Sj)-C(Sj(〗i}]。

(1)

联合采购与配送联合优化的成本分摊问题是典型的合作博弈问题，涉及两个计算环节：①对优化问题进行建模，得到成本分摊所需要的输入数值；②采用Shapley值法，基于①的输出结果得到合理的成本分摊方案。Shapley值法是合作博弈中一个成熟的分摊方法，根据式(1)可知，当参与合作的企业数量为n时，需要计算2n-1个输入数值。对物品购买成本的Shapley值法分摊而言，输入数值为各个子联盟S的采购量合并后计算的采购总金额，即2n-1个子联盟对应的采购金额C1(S)；对配送成本的Shapley值法分摊而言，输入数值为2n-1个子联盟S的配送成本C2(S)，每一个C2(S)的计算均涉及一个VRP问题，用数学语言描述即求解一个包含n个成员的VRG(Vehicle Routing Game)问题[28]，等价为求解2n-1个VRP问题，从而得到2n-1个C2(S)的相关数值。

本文涉及2n-1个联合采购与配送问题。第j个企业联盟Sj的协同总成本为C(Sj)，C(Sj)中包括物品购买成本C1(Sj)与配送成本C2(Sj)，协同总成本C(Sj)=C1(Sj)+C2(Sj)。为直观体现各子联盟的构成，采用长度为n的二进制0-1数组表示子联盟，引入子联盟序列变量j，将所有2n-1个子联盟S根据其成员构成转换为二进制数组，再按照对应的十进制从小到大排序，最后求解对应的2n-1个VRP问题。子联盟S的表示方法如图1所示。

图1中，第1个子联盟S1代表{n}，即仅包含第n个企业的子联盟；第2个子联盟S2代表{n,n-1}，即包含第n个与第n-1个企业的子联盟；同理，第2n-1个子联盟S2^n-1代表{1,2,…,n}，即包含所有企业的大联盟N={1,2,…,n}。

2 成本分摊问题中输入数值的量化

本文研究n个企业随机组成的联盟S进行联合采购的成本分摊问题。设第j个企业联盟Sj的协同总成本为C(Sj)，其中包括物品购买成本C1(Sj)，配送成本C2(Sj)，即协同总成本C(Sj)=C1(Sj)+C2(Sj)。

2.1 企业联盟Sj的物品购买成本C1(Sj)

(1)供应商提供的价格梯度表述如式(2)：

(2)

(2)hSj代表联盟Sj得到的采购价格，根据式(2)可得hSj的数学表达式：

(3)

(3)企业联盟Sj的物品购买成本C1(Sj)如式(4)所示：

(4)

2.2 企业联盟Sj的配送成本C2(Sj)

本节的配送成本计算较为复杂，需要一次性求解成本分摊所需要的2n-1个成本输入数值。用数学语言描述即可看作求解一个包含n个成员的VRG(vehicle routing game)问题，等价于求解2n-1个子联盟的VRP问题。

本文建模涉及的数学符号如下：

N为所有加入联合采购的企业，N={1,2,…,n}；

O为供应商(配送中心)；

C为配送中心的待配送企业集合，C={1,2,…,n}；

K为配送中心的车辆集合，K={1,2,…,k}；

Q为配送车辆的最大载量；

qi为第i(1≤i≤n)个企业需求量，且0≤qi≤Q；

Sj为第j(1≤j≤2n-1)个企业子联盟，且Sj≠∅；

B2D(·)为将1×n维0-1向量“·”看成2进制数值，并将其转化为十进制值；

D2B(·)为B2D(·)的逆运算，即将数值小于等于2n-1的十进制值转化为n位的二进制值，并表示为1×n维0-1向量；

Bj为与Sj对应的1×n维归属向量，当i∈Sj(1≤i≤n)时Bj(i)=1,否则Bj(i)=0，且B2D(Bj)=j，D2B(j)=Bj；

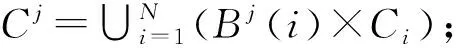
cst为任意两企业或配送中心与一个企业s,t之间的配送成本；

xstk为0-1变量，xstk=1表示配送车辆k∈Kj经过弧(s,t)，其中s,t∈Cj∪O，否则xstk=0。

模型基于的假设条件：

(1)每辆车的起点和终点均为配送中心；

(2)每辆车均不允许超过最大载量Q。

构建的模型如下：

目标函数：

(5)

约束条件：

(6)

(7)

(8)

(9)

(10)

(11)

xstk∈{0,1}∀s,t∈Cj∪O,k∈Kj。

(12)

目标函数(5)是指最小化子联盟Sj中的企业配送成本C2(Sj)；约束(6)和(7)保证每个企业被1辆车确切的服务一次；约束(8)表示一辆车没有重复经过某个节点；约束(9)表示每辆车在配送过程中不超过载量；约束(10)和(11)表示配送车辆从配送中心出发，最后回到配送中心；约束(12)表示变量的取值范围。值得注意的是，当一个企业的订购量超过一辆车的载重Q时，可将整车运输货物直接化为点对点直线距离进行配送成本的求解，再采用本模型对剩余的零担运输货物配送成本进行求解。

本模型的主要贡献是：将任意2n-1个子联盟Sj(Sj⊆N)对应的VRP问题构建为一般化模型，从而能够一次性连续求解所有2n-1个C2(Sj)，得到后续成本分摊需要的输入数据。

3 VRG问题中Shapley值法的应用

目前，企业多采用Shapley值法分摊物品购买成本，而在企业联盟N的配送成本C2(N)结算完成后，以企业商品采购量占总采购量的比重为分摊标准，得出每个企业的配送成本分摊值。当企业采购商品的配送成本占总成本比重较高时，传统权重分摊方法得到的分摊结果特点为：采购量占总采购量比重最大的企业分摊最多的成本。但是在联盟中，采购量最大的企业对配送车辆满载的贡献最大，故采用传统权重分摊方法分摊配送成本对采购量最大的企业是不公平的。由此可见，传统权重分摊方法具有其不合理性，本文致力于采用Shapley值法对配送成本进行合理分摊，为企业联盟公平分摊成本提供一个新思路。

根据本文设计的模型，对第4章算例运算流程作详细的步骤分析，如图2所示。

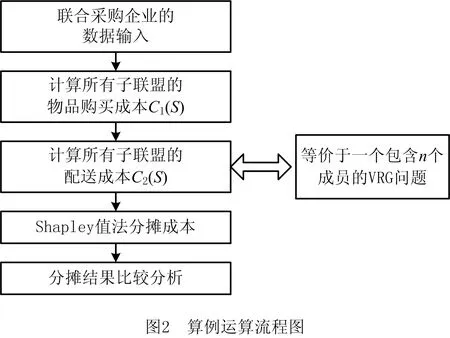
步骤1联合采购企业的数据输入。输入n个企业收货位置，商品采购量的信息。

步骤2计算所有子联盟的物品购买成本C1(S)。根据物品购买数量对应价格折扣信息，计算任意非空子联盟S(共有2n-1个)中的成员协作采购需要的物品购买成本C1(S)。

步骤3计算所有子联盟的配送成本C2(S)。子联盟的配送成本等价于求解1个包含n个顾客的VRG问题，即求解2n-1个对应的VRP问题，其对应的目标函数值记为C2(S)。

步骤4Shapley值法分摊成本。采用Shapley值法分别对大联盟N(S⊆N)的物品购买成本C1(N)、配送成本C2(N)和总成本C1(N)+C2(N)进行分摊。

步骤5分摊结果比较分析。传统采购成本分摊方法，即按每个企业购买数量占总购买量的权重分配物流配送成本。本文按上述分摊思路分别对C1(N)，C2(N)，C1(N)+C2(N)进行Shapley值法分摊，并将结果与传统分摊方法进行对比。

3.1 VRG问题

算例流程中步骤3计算所有子联盟的配送成本，等价为求解1个包含n个企业的VRG问题，从而转化为求解2n-1个VRP问题。联合采购的物流配送点数量等于参与联合采购的企业数，求解规模较小，故仅采用节约算法求解VRP问题得到最优解。最后借用MATLAB R2016a平台编程实现高效率运算。

本文求解所有子联盟配送成本的三阶段算法设计思路是：

(1)阶段1，读取所有企业的信息(物品购买数量、位置信息)，并判断企业i是否属于子联盟Sj，如果是，则保留该企业的收货位置与采购量信息；否则删除该企业的相关信息，最终形成子联盟Sj的数据信息。

(2)阶段2，采用Cluster经典算法，聚类顾客所属配送车辆。

(3)阶段3，基于经典Savings算法，用其求解所有企业子联盟的配送成本。三阶段算法流程如图3所示。

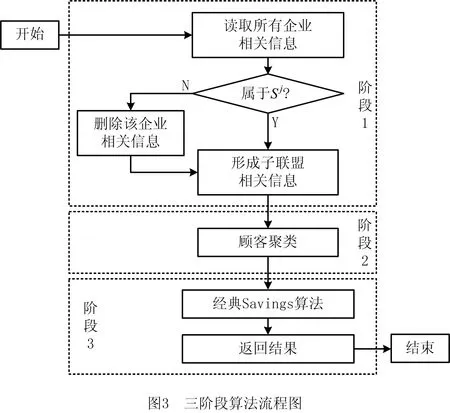
3.2 Shapley值法

Shapley值法是由Shapley提出的一种用于解决n人合作的利益分配方法。涉及的符号描述如下：假设n个参与者组成联盟S，第j个子联盟Sj的总成本为C(Sj)，第i个参与者需要分摊的成本为Φ(i)，联盟N={1，2，…，n}的总成本为C(N)，求解每个成员的分摊成本Φ(i)。一个n人参与的合作问题中，能够形成的联盟子集数有2n-1个，Shapley值法依次求解大联盟中成员i分摊的成本值，其计算量随着n的增大呈指数增长。Shapley值法的计算公式如式(1)所示。

本文考虑采用Shapley值法分摊配送成本，从而使得协同总成本在联盟企业之间的分摊更合理。Shapley值法需要求解2n-1个子联盟的物品购买成本与配送成本，运算量较大，故本文借助MATLAB R2016a编程软件实现2n-1个子联盟的成本计算，并求解每个企业的成本分摊值。最后将得出的数据导入Excel表格进行处理，绘制成表，作为进一步分析算例的基础。

4 算例与分析

4.1 算例构建

假设某配送中心覆盖的配送区域半径为10公里，每辆配送车辆的载重Q=50。基于上述条件，本文将配送半径按比例缩小，即设定在区间[0，10]随机生成n+1个点的x与y值，将其作为企业与配送中心的坐标，在区间[5,30]随机生成对应的n+1个q值，其中第n+1个点代表配送中心，将其q值设置为0。然后利用MATLAB R2016a编程，计算每个企业子联盟的物品购买成本与配送的成本，并采用Shapley值法分摊物品购买成本，分别使用Shapley值法与权重分摊法对配送成本及协同总成本进行分摊，并将分摊结果进行对比。

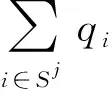
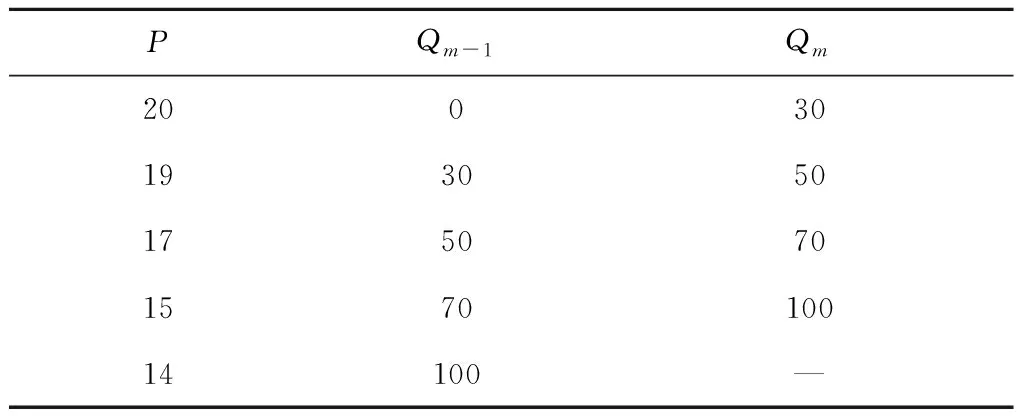
表1 价格梯度表

为了更直观地体现采用Shapley值法同时分摊联合购买与配送成本的优势，本文引入“平均偏差”指标的概念，用于衡量Shapley值法的优势，将指标简称为AD(Average Deviation)。该指标用于说明不同情况下，Shapley值法分摊配送成本与权重法分摊配送成本之间所产生的偏差率：AD越大，说明Shapley值法对应的成本分摊方案与权重法对应成本分摊方案的偏差越大；AD越小，说明Shapley值法对应的成本分摊方案与权重法对应成本分摊方案的偏差越小。因权重分摊法具有不合理性，而Shapley值的合理性已被证明，故平均偏差代表成本分摊方案的可改进程度。

假设第i个企业采用Shapley值法分摊协同总成本的分摊结果值为ai，采用权重法分摊协同总成本的分摊结果值为bi，两种不同方法分摊结果的偏差值为di，C(N)表示n个企业的商品购买成本与配送成本相加，即合作联盟N中所有企业产生的协同总成本值，故有：

(13)

di=|ai-bi|。

(14)

由此推导得出：

(15)

此时，企业采用两种不同分摊方法得到的协同总成本平均偏差

(16)

0≤AD≤100%。

(17)

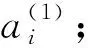
(18)

(19)

(20)

(21)

0≤AD(1),AD(2)≤100%。

(22)

因商品的特性不同，配送成本占总成本的比重α不同。据中国交通新闻网统计，我国2018年9月生鲜农产品物流成本占总成本的30%～40%，故本文选取配送成本占比20%与50%的商品作为实验对象，算例从两个不同的情景进行考虑。

情景1配送成本占总成本的20%，物品购买成本占80%。

情景2配送成本占总成本的50%，物品购买成本占50%。

(1)标准算例数据

假定配送成本占据总成本的比重为α，为更简单清晰地表示不同算例的特性，将算例的命名规则设定为“配送成本占比—位置分布均匀与否—企业数量—算例次序”，即“α-uniform-n-β”与“α-scatter-n-β”。选取算例“20%-uniform-10-1”为标准。该算例命名所代表的含义为：当采购的商品特性为“配送成本占比为20%”时，地理位置分布均匀(uniform)的10个企业进行联合采购的第1个算例。该算例包含的企业以及配送中心点位置分布如表2所示，其中：xi为第i个企业所在位置的横坐标，yi为第i个企业所在位置的纵坐标，qi为第i个企业的商品购买量，序号0为配送中心的位置，序号1～10为参与联合采购的企业位置。

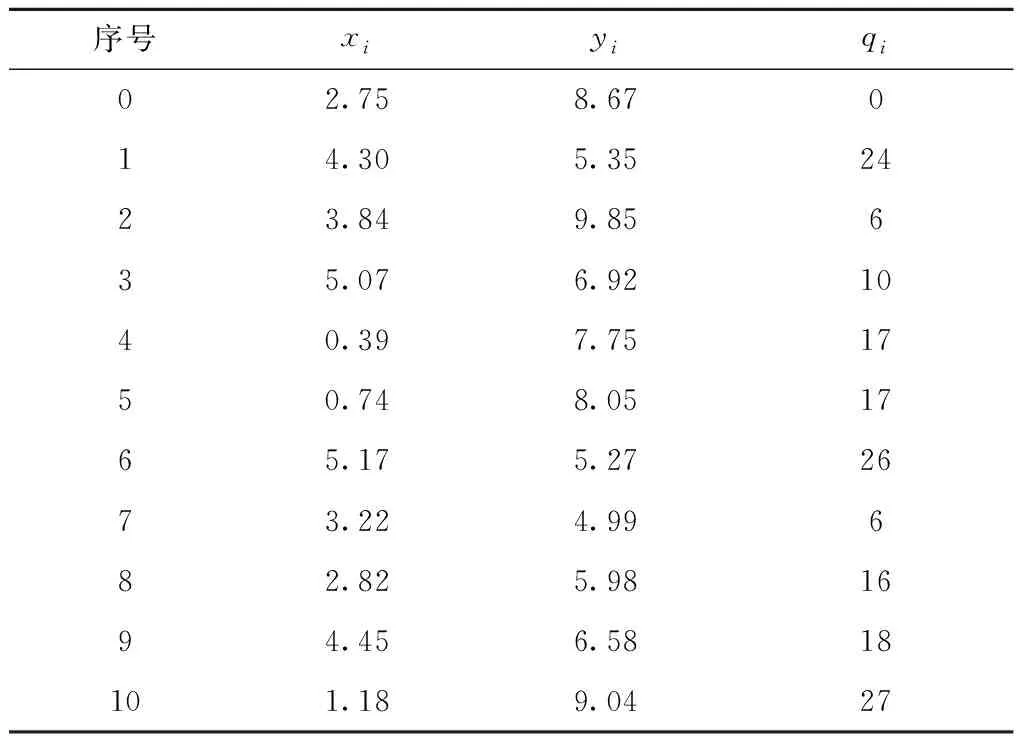
表2 算例“20%-uniform-10-1”的相关信息

根据表2的数据信息，计算得到对应的成本分摊结果，如表3所示。该算例中，当采购商品特性为配送成本占比20%时，物品购买成本采用传统权重法与Shapley值法分摊产生的平均偏差AD(1)为0.85%，而配送成本采用传统权重法与Shapley值法分摊产生的平均偏差AD(2)可高达18.70%，协同总成本采用传统权重法与Shapley值法分摊产生的平均偏差AD可达4.42%。

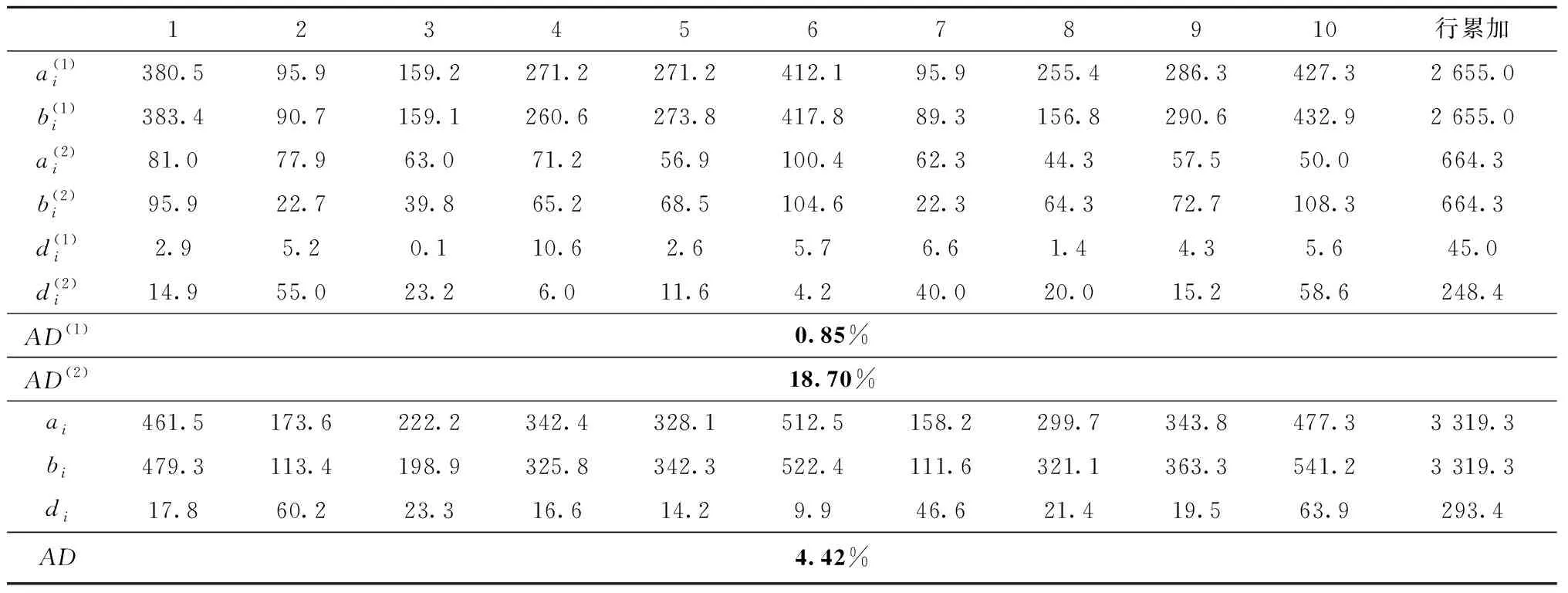
表3 算例的成本分摊结果

当前研究已经证明，Shapley值法在分摊领域中的合理程度较高，故分摊成本对应的平均偏差越大，越有必要采用合理的Shapley值法进行成本分摊。由数据对比可知，联合采购成本分摊问题中，配送成本对平均偏差的影响较大，将配送成本加入物品购买成本中进行分摊可以提高分摊的合理性。同时，联合采购是一个多频次行为，一次分摊的偏差即可达到4.42%，随着合作次数的增加，仅采用合理的分摊方法对物品购买成本进行分摊的不合理性将更加突出。综上所述，采用Shapley值法同时分摊物品购买成本与配送成本将提高企业进行合作的积极性，得到更高的经济效益。

(2)规模为10的随机算例

对α=20%，α=50%两种情况分别选取n=10的7个算例进行数据分析，同时控制“配送成本占比”指标不变，每个企业的需求量不变，仅变动企业的位置分布情况，选取位置分布均匀与不均匀的算例各7个，对算例求解出的AD(1)、AD(2)、AD数值进行分析。如表4所示，因所有算例的企业需求量不变，故算例计算得出的物品购买成本分摊的平均偏差AD(1)均为0.85%，具体的算例数据分析见4.2节。为简化算例命名，表4中的α值全部省略%，即表中α=20的含义为α=20%。

表4 规模n=10的算例数据表

4.2 算例分析

(1)对“α”指标的分析

由表4数据可知：控制“位置分布”变量，位置分布情况不变时，仅改变α指标，对配送成本分摊的平均偏差AD(2)无影响(算例设定，当企业位置分布一致时，仅变更商品的特性，配送路线不变)。故本部分仅对α指标对AD(即协同总成本分摊的平均偏差)的影响趋势进行分析，如图4所示。

对图4进行分析可得，当参加联合采购的企业位置分布不均匀时，α指标的值越大，使用Shapley值法分摊配送成本与权重法分摊配送成本得到的总成本平均偏差AD越大，最大偏差可达11.75%。同理，参加联合采购的企业位置分布均匀时，α指标的值越大，使用Shapley值法分摊配送成本与权重法分摊配送成本得到的总成本平均偏差AD越大，最大偏差可达10.57%。由此可知：当联合采购企业联盟所采购商品的运输费用占总成本比重越高，分摊方法的合理性对成本分摊结果产生的影响越大，采用Shapley值法同时分摊联合购买与配送成本，使得企业之间的成本分配方案更加合理。

(2)对“位置分布”指标的分析

根据表4中数据，控制“α”变量，当α指标不变时，分析仅改变企业位置分布对AD(2)(配送成本分摊的平均偏差)、AD(协同总成本分摊的平均偏差)两个指标的影响趋势，如图5和图6所示。

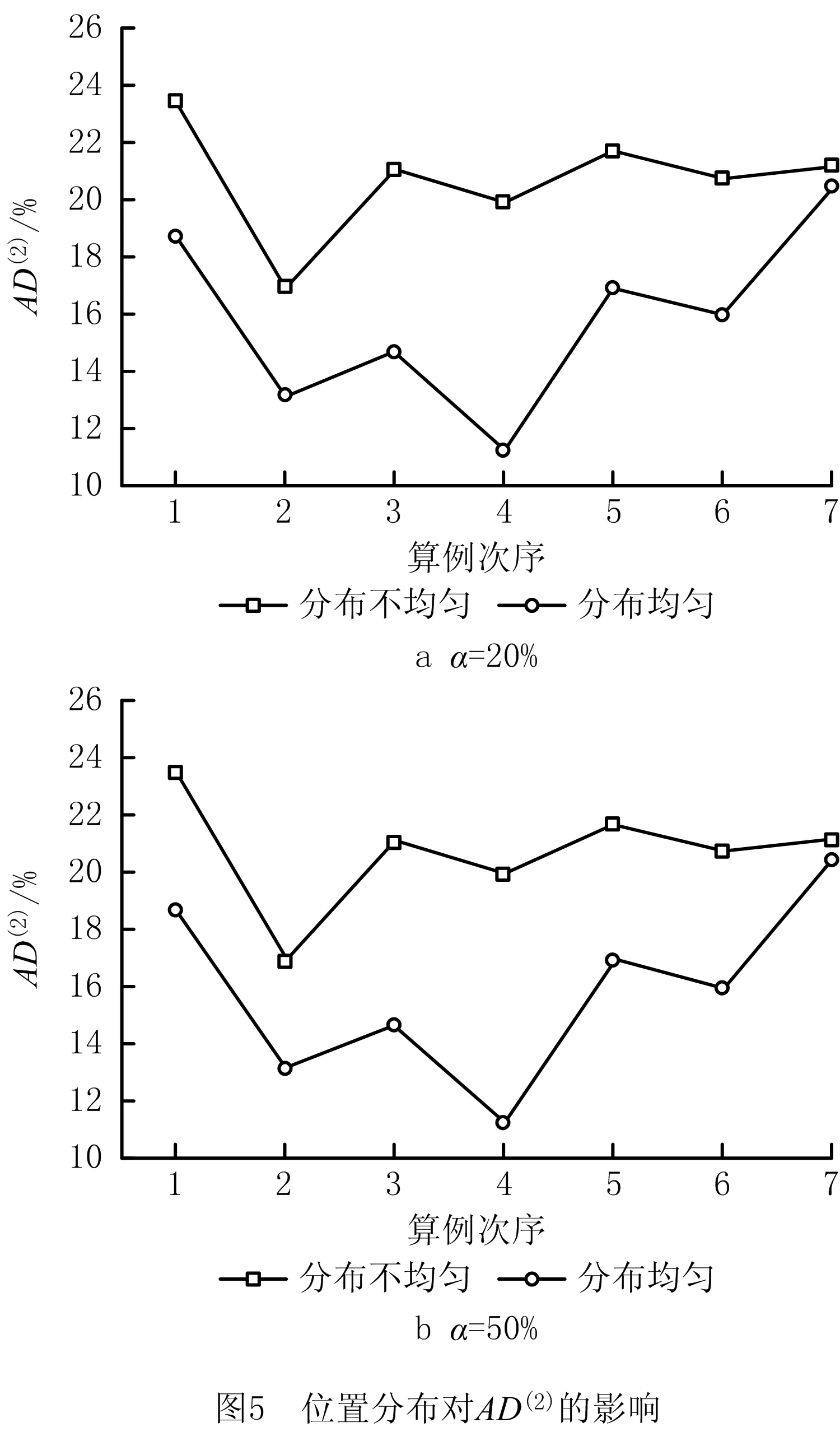
1)“位置分布”指标变动对AD(2)的影响。

分析图5可得，α指标为20%与50%时，企业的位置分布均匀与否，对配送成本分摊的平均偏差AD(2)的影响波动较大。且相较于位置均匀分布的情况，企业位置分布不均匀时，对采用两种不同分摊方法得到的配送成本分摊平均偏差AD(2)的影响程度更高，平均偏差值最高可达23.48%。即联合采购的企业位置分布对配送成本平均偏差AD(2)有一定的影响，且位置分布越不均匀，对应的平均偏差波动越大，越应采用合理的Shapley值法分摊配送成本。

2)“位置分布”指标变动对AD影响。

分析图6可知，α指标为20%与50%时，位置分布均匀与否对企业协同总成本分摊的平均偏差AD影响波动较大。且相较于位置分布均匀，企业位置分布不均匀时，对应的协同总成本分摊平均偏差AD的波动更明显，平均偏差值最高可达11.75%。即联合采购企业位置分布对协同总成本分摊平均偏差AD有一定的影响，位置分布越不均匀，对应的平均偏差波动越大，越应采用合理的Shapley值法同时分摊联合购买与配送成本，使得参与联合采购的企业对成本分配方案更加满意。

(3)分析总结

本章实验证明：当配送成本占比达20%及以上时，采用Shapley值法分摊配送成本更为合理。与现实中仅按货物购买数量作为权重的分摊方法相比，对应的配送成本平均偏差AD(2)可达23.48%，同时总成本平均偏差AD可达11.75%，即Shapley值法能更加合理地将成本分摊给各联盟企业，以提高企业参加联合采购的积极性。在现实情况中，合作采购的总金额较大，且采购是经常性活动，1%的偏差可以产生很大的实际成本。因此，对于配送成本占比高的物品，在联合采购中考虑采用Shapley值法分摊配送成本是有必要的。同时得出两个因素的影响效应：企业采购某种商品的配送成本占比越高，联合采购联盟的企业位置分布越不均匀，Shapley值法与权重法分摊配送成本带来的成本分摊平均偏差越大，越需要对联合采购与配送协同优化对应的成本进行合理分摊。

4.3 不同规模的随机算例结果

根据算例“20%-uniform-10-1”的步骤，对不同规模的算例进行求解，得出的数据如表5所示。为直观体现配送成本占比对协同总成本平均偏差的影响，本文在算例设计方面，设定相同规模算例中的企业需求量不变，则相同规模算例对应的物品购买成本对应分摊平均偏差AD(1)数值不变。

同时，当两个“位置分布—规模—算例次序”相同，配送成本占比不同，对应的算例设定企业位置分布信息不变，因而对应的算例中采用两种分摊方法分摊配送成本产生的平均偏差AD(2)相同。由表5可知，不同特性的算例求解结果均表现出一定的成本平均偏差，“α指标”和“位置分布”两个因素对成本平均偏差均有较大影响。企业采购某种商品的配送成本占比越高，参与联合采购联盟的企业位置分布越不均匀，Shapley值与权重法分摊配送成本带来的成本分摊平均偏差越大，则更有必要选取更合理的Shapley值法进行联合采购与配送协同优化的成本分摊。(表中α省略%)

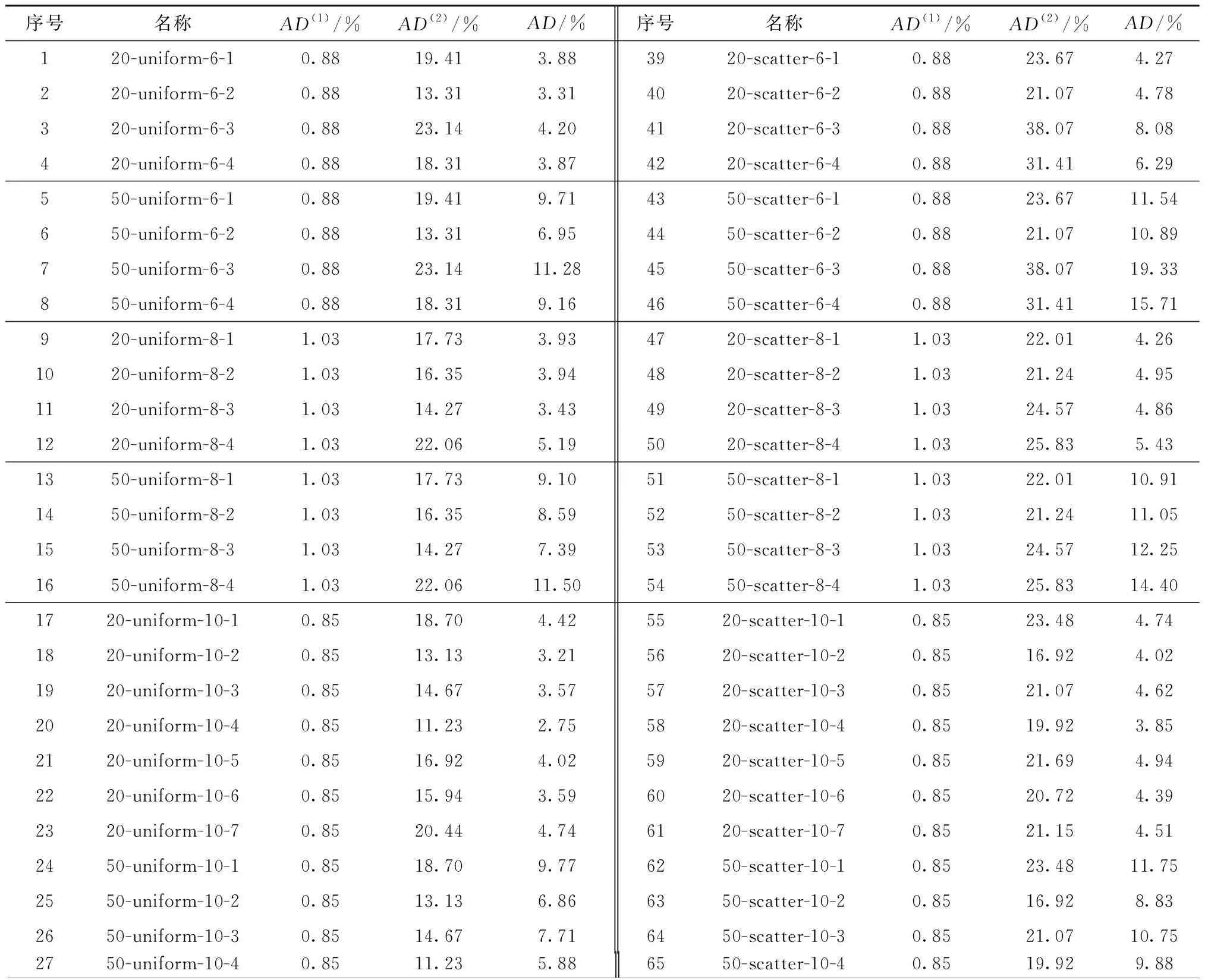
表5 随机算例数据表

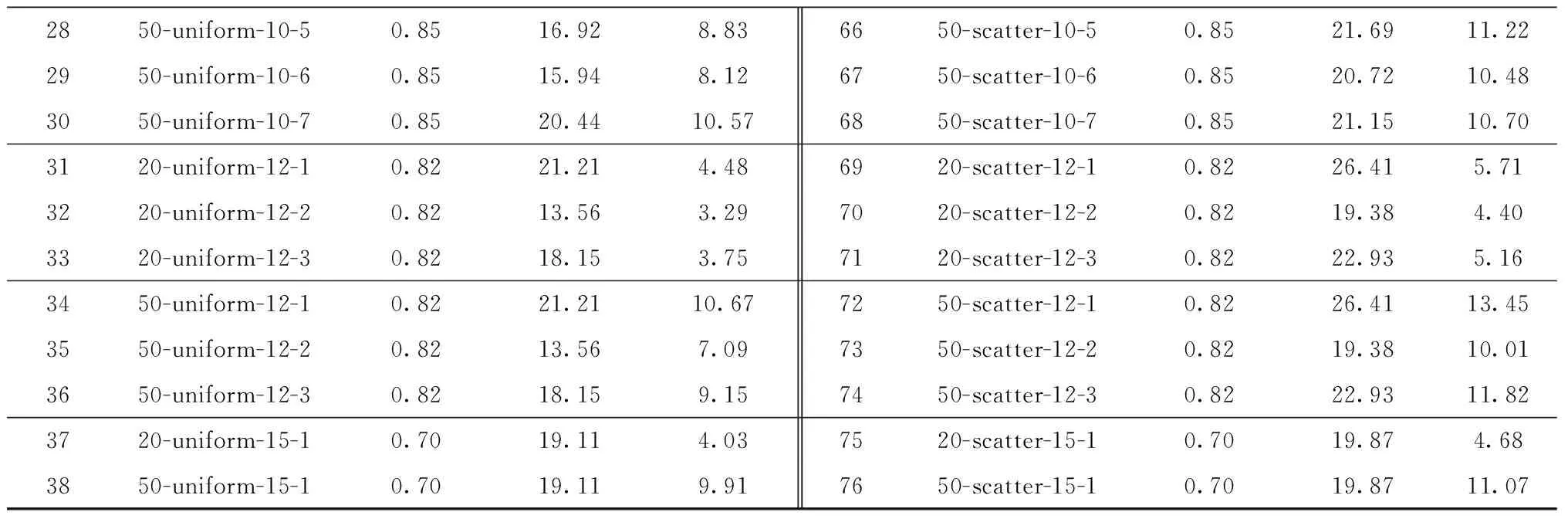
续表5

5 结束语

本文提出采用Shapley值法分摊联合采购与配送协同优化的总成本，即在分摊物品购买成本的同时，对配送成本采用Shapley值法进行分摊，为企业联盟公平分摊协同总成本提供一个新思路。根据实际联合采购问题，在考虑“企业位置分布”与“配送成本占比”等因素的基础上设计了大量算例，通过算例实验得出：与传统权重分摊方法对比，采用Shapley值法分摊配送成本更能提高成本分摊的公平性。在实践上，本文的理论成果可以用于指导企业组成联盟进行联合采购与配送协同优化的成本分摊，合理的成本分摊方法可提高联盟企业成员的满意度。同时，本文得到结论如下：

(1)采用Shapley值法分摊配送成本，与按货物购买数量作为权重的分摊方法相比，配送成本分摊的平均偏差可达23.48%，协同总成本分摊平均偏差可达11.75%。因此，Shapley值法可大幅度改进现有分摊方案的公平性。

(2)配送成本占比越大，Shapley值与权重法分摊协同总成本的平均偏差越大；当企业位置分布越不均匀时，Shapley值与权重法分摊总成本的平均偏差会更大。因此，当配送成本占总成本比率越大，联合采购的企业位置分布越不均匀时，越需要采用Shapley值法对配送成本部分进行公平分摊。

由于企业之间合作可能存在单个或多个企业违约的问题，未来的研究将在考虑企业违约这一因素的情况下，对成本的合理分摊进行更深入的研究。