产品族配置与考虑升级的再制造设计主从关联优化

张英英,夏 一,杜 纲

(1.石家庄铁道大学 经济管理学院，河北 石家庄 050043；2.天津大学 管理与经济学部，天津 300072)

0 引言

大规模定制所带来的规模经济效用使其在最近十几年受到了行业和学术界广泛关注[1]。产品族设计与基于平台的产品开发是实施大规模定制的一种有效方法[2]，在降低产品开发制造成本的同时，也可增强产品的升级换代能力[3]。基于模块化平台的产品族配置优化，是以模块化平台为基础，选择属性不同、功能类似的模块，完成产品变体的最优配置问题。因此，配置设计可以说是一个组合优化问题，目的是使单位成本效用最大[4-5]，或企业利润最大，或成本最小[6]。

随着人们对环境问题的日渐关注及环境法规的日臻严格，制造企业面临着实施有利可图的绿色制造的挑战。再制造是应对这种挑战的有效方法[7]，其利用来自废旧产品的组件或模块，生产近乎全新的产品[8]。通过再制造，企业可以降低废物处理的数量，减少资源的浪费，而产品设计是成功实施再制造的重要因素之一[9]。对于一个同时生产新产品和再制造产品的制造企业来说，优化产品设计是一项复杂的工作，对于产品族的设计优化更为艰巨。产品族配置方案会影响其后续的生产和再制造过程[10]，为了实现产品族全生命周期的利润最大化，企业需要将产品族配置和再制造模块配置进行关联设计。由于技术的快速进步，顾客的消费偏好变化越来越快，使得最初进入市场的产品族配置，很快过时或被淘汰。为吸引顾客，再制造产品需要升级或更新原产品族配置的部分属性或功能。因此，基于最初产品族配置，企业需要在再制造过程中选择合适的产品组件或模块进行升级[7,10]，即进行再制造设计。目前，考虑升级的再制造设计已经开始应用于试验仪器、军用装备和电子设备等的再制造中[11]。也有一些学者开始关注再制造升级设计的研究，如朱胜等[12]提出了军用装备再制造升级的工程技术体系，为军用设备的再制造升级设计提供了参考;KWAK等[7]研究了同时优化产品初始配置和后生命周期的再制造设计升级问题，并通过一个台式电脑的实例加以说明。对于一个同时生产新产品和再制造产品的制造企业来说，最初的产品族配置方案直接决定了再制造设计中的再制造模块和升级模块的选择，进而影响再制造的成本和收益；而再制造的模块配置设计也会影响产品族配置方案及产品族的总制造成本[10]。产品族配置与再制造设计在决策顺序上存在先后关系并且相互影响，有各自的决策目标，他们之间是主从关联关系。

目前，虽然再制造得到了行业和学术界大量关注，但关于面向再制造的产品或产品族设计优化及在再制造过程中考虑升级的研究却较少[13]。其中，有的研究只考虑在不改变产品最初配置情况下的再制造决策，如KWAK等[10]研究了在给定新产品设计的情况下，再制造产品的设计和定价问题；肖文星等[14]虽同时考虑了产品模块化架构与生态升级的协同设计，但只是从单个产品的角度出发，着眼于再制造过程中模块的升级设计，没有考虑对模块的再制造问题。还有一些研究将产品配置过程与再制造过程分成两阶段来考虑新产品和再造产品的竞争问题：第一阶段为原始设备制造商(Original Equipment Manufacturer, OEM)设计和销售新产品；第二阶段为再制造商按照既定产品设计结构，实施产品的再制造并销售再制造产品，与新产品形成竞争。如WU等[15]在考虑新产品和再制造产品竞争的情况下，研究了企业在确定产品设计的可拆解程度时OEMs的决策选择问题。即使有些研究在再制造过程中考虑了产品升级，但均是假定产品最初配置是已知的，没有考虑产品最初配置对产品后续的再制造设计的影响。RACHANIOTIS等[16]提出一个决策支持模型用来解决再制造一组系统的决策问题,该模型根据产品最初配置决策哪些零部件重用、替换、升级及废弃的问题。以往研究中所采用的两阶段方法通常会使所得解决方案非最优解[17]，并且这种方法没有考虑到产品族配置与再制造设计之间的交互耦合关系。将产品族配置设计与考虑升级的再制造设计关联优化主要有以下难点：

(1)优化方法选择 产品族设计开发中常用的优化方法主要为单目标规划和多目标规划方法，是针对只有一个决策者的单层优化方法[18-21],常用的两阶段方法本质上也是一个单层优化模型。然而，产品族配置设计与考虑升级的再制造设计关联优化问题涉及多个领域、多个决策者，且不同决策者之间相互影响，可以看成一个博弈问题。因此，单层优化模型并不能很好地刻画这类博弈问题中的不同决策者之间的耦合决策过程。

(2)主从结构 产品族配置设计与考虑升级的再制造设计关联优化过程中，不但存在多个决策者，而且这些决策者的地位不同，决策具有先后顺序。一般来说，制造企业的设计部门在初期产品设计阶段先决策产品族的最初配置设计；在产品生命周期即将结束时，该制造企业的再制造部门结合产品族的最初配置设计，来完成考虑升级的再制造设计，并根据该再制造设计方案进行再制造。该过程中，产品族配置设计决策者和再制造设计决策者可以视为两个不同的决策主体，并处于不同的决策层级，通常产品族配置设计在先，会直接影响后期的再制造设计，处在主导地位；再制造设计决策在后，会将再制造设计结果反馈给产品族配置设计决策者，处在从属地位。因此，以产品族配置设计为主，考虑升级的再制造设计为从,建立一个揭示这种主从关系的决策框架是具有挑战性的。

因此，本文针对产品族配置与考虑升级的再制造设计主从关联优化问题，基于Stackelberg理论，开发了一种主从关联优化方法(Leader-follower Joint Optimization, LFJO)，建立了以产品族配置问题为主，考虑升级的再制造设计问题为从的非线性双层规划模型。上层优化问题以最大化产品族全生命周期利润为目标，决策产品族的最初配置参数；下层优化问题以最大化再制造利润为目标决策，选择再制造模块及升级模块。然后，设计了一个嵌套遗传算法及相应的编码策略求解该模型。最后，将所提出的模型和算法应用在一个台式电脑产品族案例中，并将所得结果与两阶段方法进行比较分析，验证方法的优越性。

1 产品族配置与考虑升级的再制造设计关联优化问题

1.1 问题描述

对于一个同时生产新产品和再制造产品的制造企业，在初期产品设计阶段，针对不同的细分市场i(i=1,2,…,I)，由其设计部门设计出一个包含J个产品变体的产品族，其中细分市场i(i=1,2,…,I)的容量为Qi，且市场中存在NC个竞争者提供类似的产品。产品族中第j个产品变体表示为Pj(j=1,2,…,J)，由一组功能类似但属性不同的模块Mk(k=1,2,…,K)构成，而模块Mk有l(l=1,2,…,Lk)个模块候选项。产品族配置决策是根据市场需求，从这些模块候选项中选择最优的模块候选项组成产品变体，确定产品族结构并进行生产，之后选择合适的价格销售给顾客，追求全生命周期的产品族利润最大化的过程。全生命周期的产品族利润为初期新产品利润和后期的再制造利润之和。

在产品生命周期即将结束时，企业的再制造部门对该产品族进行回收、再制造，且同时向市场销售该产品族的全新产品和再制造产品。该公司的再制造流程由回收、再制造操作两种活动组成。企业按照给定回收率对最初投入市场的产品变体进行回收，然后对其再制造。再制造过程首先将产品拆卸成若干个产品模块，每个模块作为一个独立的再制造修复单元可选的修复操作有再利用和原材料回收两种。只有被确定为可再利用的模块才能选择再利用操作，不可再利用的模块将卖给第三方原材料回收商。此外，制造企业决策再制造产品中的模块升级时，如果模块Mk(k=1,2,…,K)被确定为升级模块，则该模块是不能被再利用的，且需要决策升级到第几代。因此，模块的升级决策将影响再利用模块的选择及所需再利用模块的数量。最后，将这些升级模块和再利用模块进行再装配，形成产品族中的再制造产品。当再利用的模块不足时，需要生产相同规格的新模块。综上，企业再制造部门需要决策哪些模块再利用，哪些模块将作为原材料回收以及哪些模块升级，来最大化产品族的再制造利润。

通过上述优化问题的描述可知，产品族配置问题与考虑升级的再制造设计问题所处的决策层次不同，决策顺序亦有先后，一般先决策产品族配置设计，后进行再制造设计。产品族配置方案直接影响再制造设计的再制造模块和升级模块的选择，以及进行再制造的成本和收益；而再制造设计也会影响产品族配置设计结果及总制造成本。此外，产品族配置由制造企业的设计部门来决策，其决策目标是从全局视角出发考虑产品族全生命周期利润最大化；而考虑升级的再制造设计是由再制造部门决策的，其目标则只关注于再制造阶段的利润，并不会考虑产品族设计和制造阶段的成本及收益(即新产品的利润)，这就使得产品族设计生产阶段的利润与再制造设计的利润在一定程度上存在冲突。因此，本文基于Stackelberg博弈理论建立了双层规划模型，解决产品族配置与考虑升级的再制造设计关联优化问题。

1.2 问题假设

本文主从关联优化问题基于以下几个假设条件来建立优化模型：

(1)产品具有模块化结构，且产品模块是最小的拆卸单元，产品升级是通过替换相应的模块来实施的。

(2)再制造模块的顾客感知效用与新模块相同。

(3)再制造是即时的，可以忽略再制造生产的提前期。

(4)所有不可再利用的模块以及多余的可再利用模块卖给第三方原材料回收商，进行原材料回收。

2 主从关联优化模型的建立

2.1 变量及参数说明

2.1.1 参数

在本文中，主从关联优化模型中用到的参数如表1所示。

表1 参数说明

续表1

2.1.2 决策变量

主从关联优化模型中的决策变量如表2所示。

表2 决策变量符号说明

2.2 顾客购买选择模型

(1)

(2)

其中：uikl为细分市场i中顾客对模块k的模块候选项l的效用值;wjk为模块k在产品j中的比重;viklzjkl为细分市场i中顾客对模块k的第l个模块候选项升级到第zjkl个版本的效用;εij和ηij均为误差项。

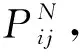
(3)

(4)

由于产品族进入市场初期不存在再制造产品，而到产品族生命周期后期采用了再制造设计，使得市场中同时存在新产品、再制造产品和竞争者产品。

2.3 成本估算

2.3.1 制造成本计算

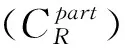
(5)

(6)

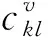
2.3.2 再制造成本计算

再制造过程涉及产品回收、修补翻新、再组装等活动，这里将这几个活动所产生成本定义为再制造成本，具体表示如下：

(7)

式中:大括号中第一项为回收产品的可再利用模块能够满足再制造产品生产情况下(gjkl=1时)的再制造成本；第二项表示不能满足生产的情况下(gjkl=0时)的再制造成本。

2.4 原材料回收收入

由所提出的假设可知，制造企业按照一定的回收率将废旧产品回收。拆卸旧产品所得到的模块并不是所有都能再利用，因此制造企业会将不能再利用的模块卖给第三方原材料回收商。此外，如果回收获得可再利用模块的数量大于再制造产品所需的模块数量，则多余的可再利用模块也需要卖给第三方原材料回收商。因此，原材料回收收入具体表示如下：

(8)

2.5 双层规划模型

结合上下层优化问题涉及到的式(1)～式(6)，本研究中的主从关联问题的双层优化模型具体表示如下：

maxπT=πN+(1+θ)-t·πR。

(9)

s.t.

(10)

(11)

(12)

(13)

xjkl+τjkl·t-1≤αkl≤xjkl+τjkl·t;

(14)

Xj,xjkl∈{0,1};

(15)

αkl∈{非负整数}；

(16)

(17)

(18)

s.t.

βkl=αkl·yjkl+zjkl;

(19)

yjkl·zjkl=0;

(20)

Yj,yjkl,gjkl∈{0,1};

(21)

βkl,zjkl∈{非负整数}；

(22)

(23)

其中:式(9)为上层优化问题的目标函数，产品族全生命周期总利润由新产品利润和再制造利润两部分组成，其中再制造利润以年利息率θ进行折现；式(10)为新产品利润，即新产品的销售收入与新产品制造成本之差；式(11)为各个可选模块必须并且只能选择一个模块候选项；式(12)为产品族中产品变体的差异化约束；式(13)为产品族中产品变体的总数量小于或等于产品族的最大产品数；式(14)为产品族中模块候选项代际差的范围约束；式(15)～式(17)为产品族中新产品变体，模块候选项是否被选则的0-1约束，代际差异取值约束及新产品的零售价格为正约束；式(18)为再制造利润，即采用再制造所获得的收入与成本之差，其中采用再制造所获得收入由再制造产品销售收入和原材料回收收入两部分组成，采用再制造的成本由再制造产品中新模块的制造成本和再制造成本两部分构成；式(19)和式(20)共同约束产品模块kl是否升级及升级到第几代；式(21)～式(23)为下层决策变量及参数的取值范围约束。

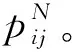
3 求解算法设计

第2章所建立的双层优化模型为0-1整数非线性规划模型，这类模型的求解已被证实是一个NP难题[6]。由于模型中的决策变量规模庞大、复杂性高，且其取值范围非连续，传统的双层规划求解方法如分支定界法、罚函数、KKT条件等难以求解这类组合优化问题[17]。遗传算法因搜索速度快、鲁棒性强、收敛效果好等优点[24]，目前已被广泛运用到产品开发的各类工程优化问题中[2,4-6,9]。因此，本文开发了一个双层嵌套遗传算法，将下层考虑升级的再制造设计问题以序贯的形式嵌入到上层产品族配置优化问题中进行求解，并将所得的考虑升级的再制造设计方案传回上层优化问题。该双层嵌套遗传算法的具体流程如图1所示。

(1)种群初始化 设置配置设计参数及上下层优化遗传算法的种群规模和最大迭代次数。随机生成产品族配置设计决策变量所对应的初始种群X，将每个可行个体传递给下层，并执行下层优化的遗传算法，得到下层变量最优值所对应的个体。采用式(9)所表示的产品族全生命周期利润作为适应度函数，基于上层问题的约束条件，计算每个个体的适应度值。

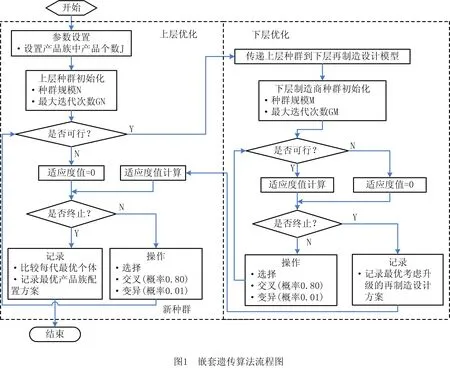
(2)上层算法的选择与进化 评估上层每个染色的适应度后，利用基于适应度值排序的选择规则，选择相应的染色体作为父代染色体。

(3)上层算法的进化 针对上层所选择的父代染色体，进行两点交叉和随机变异操作，产生新的子代染色体。

(4)下层算法优化过程 对于上层生成的每个子代染色体，传递给下层优化，并随机生成与下层考虑升级的再制造设计变量对应的初始种群，执行下层遗传算法的交叉和变异操作，得到下层考虑升级的最优再制造设计方案所对应的个体。在此过程中，采用式(18)再制造利润作为下层适应度函数。

(5)子代适应度值的评估 对于子代的每个染色体，结合(2)中得到的上层产品族配置设计结果和(4)中得到的下层考虑升级的再制造设计的最优个体，计算上层目标函数值，评估子代染色体的适应度值。

(6)种群更新 评估子代适应度值后，将上层子代种群和父代种群成员放在一起，然后按照适应度值的大小挑选优良种群个体构成新的上层种群。

(7)判断是否满足终止条件 判断遗传算法是否达到最大迭代次数。如果达到，记录最优解及相应的最优值；否则重复步骤(2)～步骤(6)，直到达到最大迭代次数。

3.1 嵌套遗传算法的编码

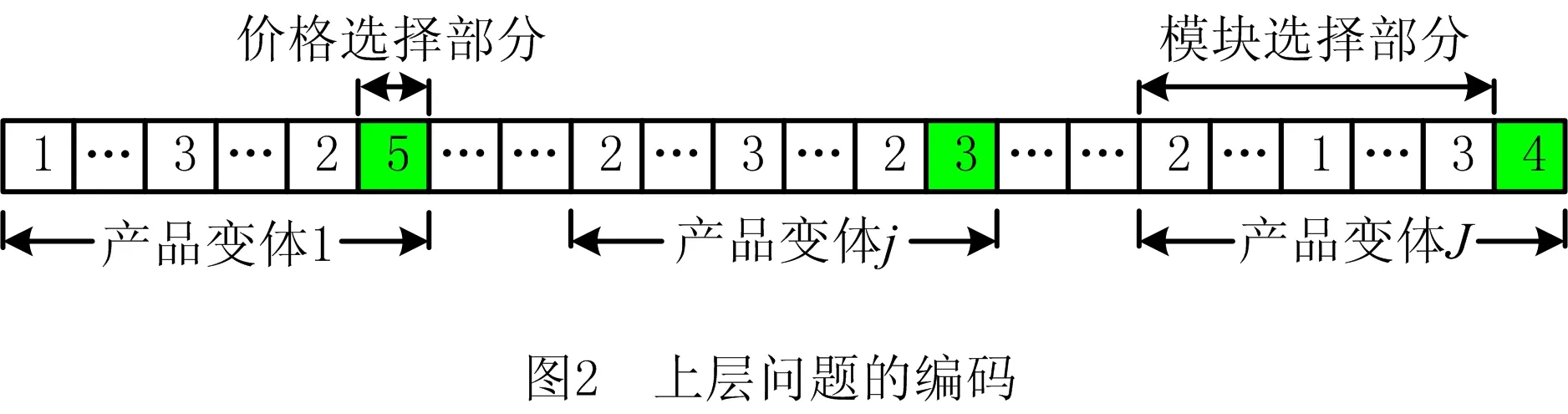
应用遗传算法求解所建立的双层优化模型，需要将决策变量表示为一定长度的字符串，即染色体。在此设计一种新的编码方法，重新定义上、下层决策变量。在上层编码中，令X表示产品变体中模块候选项及新产品价格的选择方案。如图2所示为产品族配置问题的通用整数编码策略。该编码策略按照产品族中产品变体的个数，将一条染色体分成J个部分，其中第j部分表示第j个产品变体的配置选择。每个产品变体由模块选择部分和价格选择部分两个子部分构成，其中，模块选择部分由K个子部分组成，每个子部分分别代表产品变体的不同模块，对应染色体中的各个基因。如图2所示，白色方格部分为模块选择部分，每个方格分别代表对应产品变体的不同模块，即每个基因；有色方格部分为价格选择部分。模块选择部分采用正数编码策略，第k个基因值l表示第k个可选模块的第l个模块候选项被选中。如图2所示，在产品变体j中，第一个方格表示产品变体j的中第1个模块，即产品变体j的染色体的第1个基因，其值为2，说明产品变体j的第1个模块的第2个模块候选项被选中。由于零售价格为连续变量，在进行编码之前，需要结合企业经验和历史产品的定价数据，由企业直接给定产品变体的离散价格备选集合。然后，再对离散价格采用正整数编码。价格选择部分的基因值p表示选择第p个离散价格作为对应产品变体的零售价格。例如，企业所给定的新产品价格集合为{$860，$880，$900，$920，$940}，如图2中产品变体j，价格选择部分的基因值为3，则$900就作为产品变体j的零售价格。因此，包含J个产品变体的产品族的染色体长度为J·(K+1)。

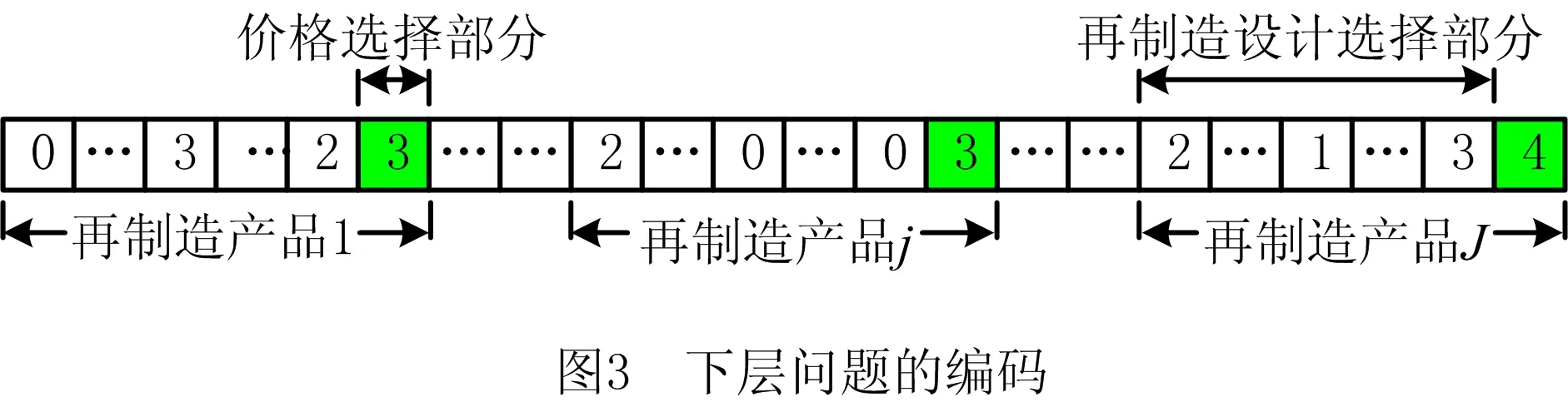
在下层考虑升级的再制造设计的遗传算法编码中，令Y表示再制造选择方案及再制造产品价格的选择方案(如图3)。该编码策略按照产品族中再制造产品的个数，将染色体分成J个部分，第j部分表示第j个再制造产品的再制造模块选择方案。每个部分包含再制造模块选择子部分和价格选择子部分两个子部分，如图3所示，白色方格部分为再制造设计选择部分，有色方格部分为价格选择部分。第j个再制造产品由K个模块构成，第j个再制造产品的第k个基因值s表示第j个再制造产品的第k个模块所选择的再制造方式。若基因值s=0，则表示第k个模块选择再制造；若基因值s的取值为正整数，则表示第k个模块选择升级，并升级到第s代。图3中，再制造产品j的第1个基因值为2，表示再制造产品j的第1个模块选择升级并升级到第2代。类似于上层遗传算法对价格的编码，下层优化问题中的再制造产品价格也是先结合企业经验和历史数据，直接给定再制造产品的离散价格备选集合，然后采用对离散价格正整数编码的形式。价格选择部分的基因值p表示选择第p个离散价格作为对应再制造产品的零售价格。因此，包含J个再制造产品的染色体长度为J·(K+1)。

3.2 算子的选择

这里所采用的选择算子为轮盘赌选择。种群中每个个体的适应度值与整个种群中个体适应度值的总和之比为其被选入下一代的概率。因此，个体的适应度值越高，被选入下一代种群的概率也就越大。

为避免染色体早熟，所提出的双层嵌套遗传算法采用多点随机交叉算子来生成新的一对子代染色体。交叉之后，以一个很小的概率在每个子代染色体中随机选择变异点进行变异，即选择变异算子。通过变异算子可以随机改变相应的模块或价格的选择。交叉和变异操作不断重复，直到种群收敛或达到最大迭代次数。

4 案例分析：台式电脑

4.1 案例描述

为验证本文所提方法的有效性和可行性，将其应用到一个包含两个产品变体的台式电脑产品族的设计中，并假设该台式电脑产品族最初销售的所有产品在4年后(即t=4)均可回收。具体来说，该台式电脑产品族的架构包含6个可选模块：CPU(M1)、内存(M2)、主板(M3)、硬盘(M4)、显卡(M5)、显示器(M6)及1个公共模块电脑机架(M7)。各个模块所具有的模块候选项个数分别为3，3，4，4，3，3，1，台式电脑的模块具体信息如表3所示。

为了获得一个市场细分内顾客对产品模块的偏好，通过市场调研，采用联合分析法，利用SPSS软件进行正交分析和部分因子实验，获得该市场细分内产品模块各的成分效用值，如表4所示。估计新产品和再制造产品的市场容量分别为50 000和10 000。表5给出了t=4情况下，产品模块的各项操作的成本及参数信息，其中第2列和第3列分别为单位制造成本和单位再制造成本，这些数据可以根据对企业实际制造或再制造过程中的成本通过联合分析获得，制造固定成本为200 000美元；第4列为该台式电脑制造公司将不可再利用的模块及多余的可再利用模块卖给第三方原材料回收商的价格；最后两列分别为t=4情况下，年平均换代率和可再利用率。此外，该制造企业在t=4情况下的产品回收率为15%。结合企业经验及历史数据，假定新产品的备选价格集合为{$860，$880，$900，$920，$940，$960，$980，$1 000};再制造产品的备选价格集合为{$280，$290，$300，$310，$320，$330，$340，$350}。

表3 产品模块及模块候选项信息

表4 产品模块各代的成本效用

表5 模块的各项成本及参数信息(t=4)

4.2 实施与结果

利用第3章设计的嵌套遗传算法求解该台式电脑产品族配置及考虑升级的再制造设计。设置种群规模为30，迭代次数为200代，交叉变异算子分别为0.8和0.01；MNL选择规则中参数μ=6.45；年利息率θ=3%。

模型上层产品族配置模块候选项变量及价格变量的下限为：[1 1 1 1 1 1 1 1，1 1 1 1 1 1 1 1]；上限为：[3 3 4 4 3 3 1 8，3 3 4 4 3 3 1 8]。两个产品变体的变量编码中间用逗号隔开，其中每个产品变体编码的前7位代表模块候选项的编码，第8位代表离散价格的编码。模型下层再制造方案变量及再制造产品价格变量的下限为：[0 0 0 0 0 0 0 1，0 0 0 0 0 0 0 1]；上限为：[3 3 3 3 3 3 3 8，3 3 3 3 3 3 3 8]。再制造的两个产品变体的变量编码中间用逗号隔开，每个变体编码的前7位代表再制造选择方案，第8位代表再制造产品的价格选择。

如图4所示为本研究所设计的双层嵌套遗传算法的进化过程。从图4的收敛过程来看，上层产品族配置的评价指标值——产品族生命周期总利润不断增加，最后收敛为一条水平直线;而下层再制造利润函数值则随着上层产品族生命周期总利润的增加而上下波动。在第109代时，上层产品族生命周期总利润收敛于3.250 921×106，同时下层再制造利润值也随之收敛于7.204 7×105。该过程反映了该双层优化模型上下两层目标函数之间的相互权衡。

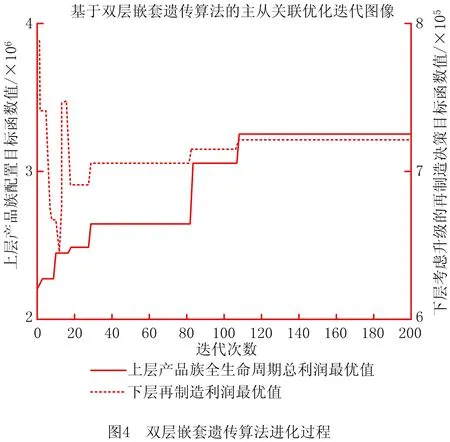
最优的产品族配置方案和对应的考虑升级的再制造设计方案如表6所示。产品变体1中，除了显卡和光驱所选择的模块候选项不是顶级配置外，其他模块所选择的都是顶级配置，因此定价较高($1 000)；产品变体2中，硬盘、显卡和光驱所选的模块候选项不是顶级配置，因此定价略低($860)。相对应的考虑升级的再制造设计中，产品变体1中内存和显卡需进行升级，分别升级到G1代和G3代，其他模块进行再制造；产品变体2则仅将内存升级到G3代，其他模块选择再制造。

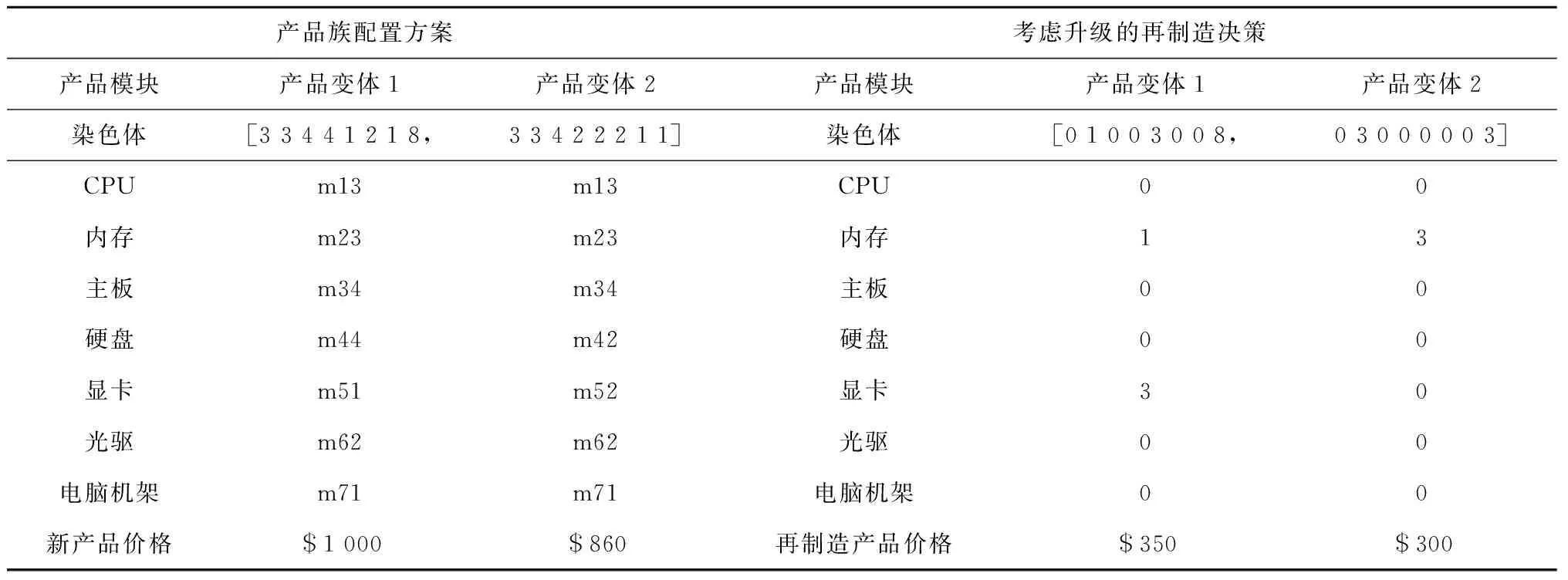
表6 产品族配置与考虑升级的再制造主从关联优化结果

4.3 分析与比较

为了验证所建模型和求解算法在解决产品族配置和考虑再制造设计关联优化问题的优越性，将这种LFJO方法得到的结果与通常使用的两阶段方法(Tow Stage Method, TSM)进行比较，结果如图5所示。TSM法是将产品族配置与考虑升级的再制造设计看成独立的两个阶段，先进行产品族配置的优化，然后根据得到的配置方案，选择考虑升级的再制造设计方案。第一阶段，根据企业再制造的历史数据，估计再制造利润，并将其作为参数代入式(9)中，在此基础上进行产品族配优化。第二阶段，将第一阶段所得的产品族配置方案作为依据，以再制造利润最大化为目标，选择最优的考虑升级的再制造设计方案。TSM法的目标函数仍为式(9)，只是将上下层的约束条件合并即可。与TSM法相比，LFJO法得到产品族全生命周期总利润从3.136 747×106增加至3.250 921×106，增加了3.64%；而且再制造利润由6.904 73×105美元增加至7.204 7×105美元，增加了4.34%。这主要是由于TSM方法在进行产品族配置时，再制造利润的计算是通过历史数据估算的，整个优化过程中并没有考虑到第二阶段的考虑升级的再制造设计对产品族配置中模块的成本和效用的影响，从而不能及时动态地调整产品族配置方案。由图5可以看出，本文所提出的LFJO法在优化结果上都要优于TSM方法，主要是因为考虑了产品族配置与考虑升级的再制造设计耦合交互关系。通过上述比较，可以看出在解决此类协同优化问题时，本文所提出的LFJO方法更具有优势。

5 结束语

针对产品族配置与考虑升级的再制造设计主从关联优化问题，基于Stackelberg理论，建立以产品族配置为主优化问题，考虑升级的再制造设计为从优化问题的非线性双层规划模型，并通过所开发的双层嵌套遗传算法对该模型进行求解。最后，将上述模型及求解方法应用到了一个台式电脑产品族案例中，说明了模型及算法的可行性及有效性。所提出的方法适用于大规模定制背景下，具有核心竞争力的制造企业，其产品族配置设计在产品设计领域和再制造设计决策中处于主导地位的情形。如制造企业完成产品配置设计和核心模块生产，再通过众包的形式，由其他企业完成非核心的产品模块及零部件、再制造模块、升级模块的供应。其中，产品配置设计为主，不同模块的选择基于产品配置设计，为此所提出的方法可应用于电子设备(如服务器、电脑等)，机械装备(如汽车发动机、航天航空器等)等产品的设计、制造及再制造的决策过程中。

本文创新之处在于从产品族全生命周期视角出发，研究了周期初期的产品族配置设计与周期末端的再制造设计之间的关联优化问题，通过定义代际差的概念来刻画再制造设计中产品升级模块的选择过程。同时，提出了LFJO方法来揭示产品族配置设计与考虑升级的再制造设计关联优化问题的内在耦合交互关系。与传统的TSM法相比，LFJO方法更符合所研究问题的分布式协同决策过程。通过台式电脑产品族算例结果显示，LFJO方法能够得到更好的考虑再制造设计的产品族配置设计方案。

基于对产品族配置与考虑升级的再制造设计的主从关联优化研究，提出了一些未来的研究方向：

(1)未来研究中，将考虑改善对市场趋势估计的方法。本研究从产品族的全生命周期视角出发，针对产品族配置与考虑升级的再制造设计主从关联优化问题，选取了产品族开发初期和生命周期末期两个时间节点来估计模块的可再利用性和其市场价值趋势，并没体现其随时间变化的趋势。因此，未来研究可以考虑对开发预测这种趋势的模型，如利用动态模型，数据挖掘技术，时间序列分析等技术和方法。

(2)由于顾客感知效用，废旧产品的回收数量及质量存在随机性和不确定性，在未来的研究中，可以设计随机模型或通过鲁棒设计来应对这种随机性和不确定性。