基于绝对节点坐标法的变截面拱面外弯扭振动分析

刘 茂, 王忠民

(西安理工大学 土木建筑工程学院，西安 710048)

拱形结构以其优美的造型、合理的受力特点和相对良好的经济指标，被广泛应用于土木工程、机械设备和航空航天等领域中。例如拱桥、吊车拱形吊臂、拱形太阳能电板等。在工程实际中，拱形结构截面多以变截面的形式出现，如拱桥则是两端横截面积较大，中间横截面积较小的拱结构。当这种拱结构受到侧向外力作用时，会发生面外的弯扭振动，其动力学特性研究具有重要的理论意义和实用价值。

自19世纪以来，许多研究人员对拱的振动问题做了大量的研究。Irie等[1]应用传递矩阵法研究了两端固定圆形和矩形横截面的Timoshenko圆形拱的面外自由振动特性。赵章泳等[2]研究了弹性支承对圆弧拱自由振动特性的影响规律。Laura等[3]使用Ritz方法，研究了厚度呈线性变化并带有集中质量的对称圆弧拱的自由振动特性。Eftekhari[4]考虑了横向剪切和转动惯性的影响，通过初值方法研究了具有均匀横截面的圆弧拱的面外弯扭自由振动。危媛丞等[5]使用Rayleigh-Ritz法分析了配重影响下两端固定圆拱的面外自由振动问题。陈耀等[6]对固接抛物线浅拱的静力及动力稳定性问题进行了研究。康婷等[7]运用样条有限点法分析了恒载效应对拱结构自振频率的影响。

对变截面拱面外弯扭振动问题，其运动微分方程为变系数的偏微分方程，一般的数值计算方法效率较低。1996年，Shabana首次提出了基于大变形有限元和连续介质力学的绝对节点坐标法(absolute nodal coordinate formulation, ANCF)，该方法选取全局坐标系下的位置矢量及梯度作为节点坐标，对大位移、大转动和大变形问题具有较好的适用性，并且质量阵为常数阵，没有科氏力和离心力的影响。Berzeri等[8]系统地归纳了基于欧拉-伯努利梁的平面一维梁单元弹性力的表达形式。李彬等[9]利用能量守恒原理验证了ANCF在分析大变形柔性梁系统刚柔耦合动力学问题中的正确性。赵春璋等[10]基于ANCF研究了变截面梁的动力学特性。王忠民等[11]基于ANCF分析了伸展悬臂梁的挠度响应。李鹏飞等[12]通过对比分析发现ANCF法对柔顺机构建模与分析更具有适应性。张君茹等[13]讨论了ANCF斜率不连续问题的解决办法。

本文基于ANCF建立Euler-Bernoulli拱单元的质量矩阵和刚度矩阵，应用Lagrange方程得到变截面拱面外弯扭的运动微分方程，分析了两端固定的变截面圆弧拱的面外自由振动特性，获得了圆弧拱中心角、半径、高宽比以及均布径向载荷等参数对变截面圆弧拱面外弯扭振动的频率的影响，最后分析了变截面抛物线型非圆弧拱的弯扭振动特性。

1 变截面拱面外弯扭变形描述

1.1 基本假设

为便于计算，对变截面拱面外弯扭振动模型作以下几个基本假设：拱的面外弯扭振动为小变形情形；材料的应力-应变关系服从胡克定律，即材料为线弹性；拱面外弯扭变形时，其横截面保持为平面，轴线无伸缩变形。

1.2 ANCF的单元形函数

(a)矩形变截面拱模型

在图1(a)中，将矩形变截面拱等分为n个等弧长拱单元，建立单元坐标系osyz，se为每个单元的轴线弧长，s为单元弧坐标，如图2所示。

图2 拱单元模型

设拱单元轴线上任意一点P的面外线位移u和面外扭转角θ的列阵表示为

(1)

式中，S(s)、N(s)是单元弧坐标s的函数，与时间无关，可表示为

(2)

式中，

式中，λe=s/se。

(3)

式中，i,j为拱单元两端的节点编号，e(e=1,2,3,…,n)为单元编号。

2 变截面拱面外弯扭振动微分方程

2.1 拱单元的质量矩阵和刚度矩阵

设拱材料的密度为ρ，横截面积为A(s)，则拱单元的动能为

(5)

拱结构面外挠曲率Ky和绕s轴的扭曲率Ks分别为[14]

(6)

式中，u′=du/ds，u″=d2u/ds2。

(7)

式中:EIy(s)为拱面外弯曲刚度；GJs(s)为扭转刚度。

(8)

拱单元的总势能表示为

(9)

式中，Iy(s)=b(s)3h(s)/12，Js(s)=βb(s)3h(s)，β为扭转因数，设高宽比η=h(s)/b(s)，β与高宽比η的值有关[15]。

拱单元的刚度矩阵为

(10)

2.2 运动微分方程和特征方程

设q为总体节点坐标列阵，Be为总体节点坐标列阵q和单元节点坐标列阵qe之间的转换矩阵，则有

q=Beqe

(11)

于是，拱的总动能和总势能表示为

(12)

式中:M为总体质量矩阵;K为总体刚度矩阵：

(13)

Lagrange函数为

(14)

把式(14)代入Lagrange方程

(15)

得到拱结构的运动微分方程

(16)

方程(16)的解设为简谐运动形式

q=Asin(ωt+φ)

(17)

式中:A为幅值列阵;ω为拱面外弯扭振动的频率;φ为初相位。

把式(17)代入式(16)，利用线性齐次方程非零解的充要条件，得到变截面拱面外弯扭自由振动时的特征方程

det(K-ω2M)=0

(18)

3 算 例

3.1 矩形等截面圆弧拱

表1 两端固定矩形等截面圆弧拱面外弯扭振动频率随单元数目变化情况

图3 两端固定等截面圆弧拱振型图

从表1的数据可以看出，基于ANCF计算等截面圆拱的频率，划分的单元数目较少时(n=4)便可得到较好的结果。随着单元数目的增多，ANCF的计算结果与文献[16]解相对误差逐渐变小，当拱单元的单元数n=24时，其相对误差仅为0.46%。从图3可以看出，一阶振型形状近似为半波正弦曲线，二阶振型近似为一个周期的正弦曲线，三阶振型近似为一个半周期的正弦曲线；对于奇数阶(如一阶和三阶振型)，对称于圆弧拱中心角的对称线；对于偶数阶振型(如二阶)，反对称于对称线。

3.2 矩形变截面圆弧拱

(19)

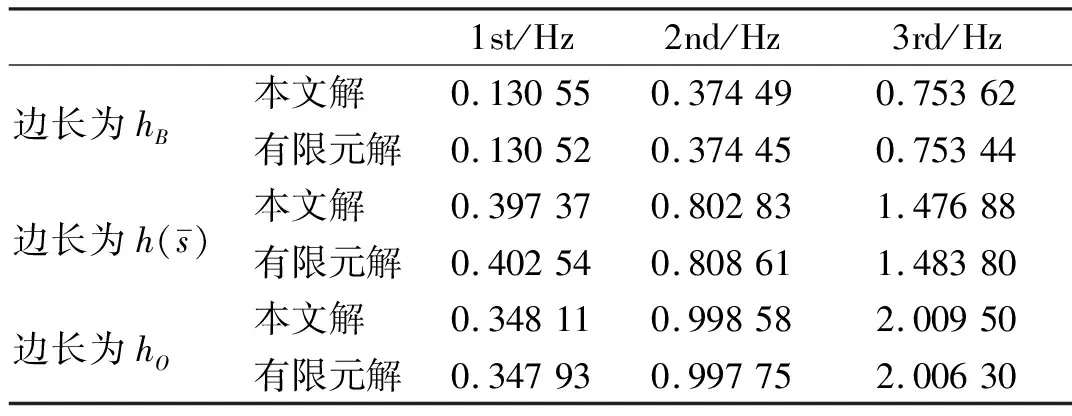
表2 两端固定正方形变截面圆弧拱面外弯扭振动频率

图4 两端固定正方形变截面圆弧拱弯扭振型图

由表2可以看出，计算结果与有限元解(作者用ANSYS软件计算的结果)相对误差较小；正方形变截面圆弧拱的一阶频率比以边长为hO和边长为hB的等截面圆弧拱的频率要大，而二阶、三阶频率处于两者中间。对比图3与图4可以看出，等截面圆弧拱和变截面圆弧拱振型图的形状基本一致。

下面讨论不同参数对结构频率影响规律。

中心角对变截面圆弧拱的频率的影响。在保证半径不变、高宽比η=1的条件下，计算得到中心角对变截面圆弧拱的频率的影响如图5所示。

图5 正方形变截面圆弧拱频率随中心角的变化关系

从图5中可以看出，变截面圆弧拱的频率随着中心角的增大而减小，并且其改变对二、三阶频率影响较大，对一阶频率影响较小；随着中心角的增加，曲线越来越平缓，说明中心角越大时，其对圆弧拱频率的影响越小。

半径对变截面圆弧拱频率的影响。在保证圆心角不变、高宽比η=1的条件下，计算得到半径对变截面圆弧拱频率的影响如图6所示。可以看出，频率随着半径的增大而减小，且其改变对二、三阶频率的影响较大，一阶频率影响较小。

图6 正方形变截面圆弧拱频率随半径的变化关系

横截面高宽比对变截面圆弧拱的频率的影响。在保证高度与正方形变截面圆弧拱的边长相同、圆心角和半径不变的条件下，计算得到高宽比对变截面圆弧拱频率的影响如图7所示。可以看出，变截面圆弧拱的频率随着高宽比的增大而减小，其改变对二、三阶频率影响较大，对一阶频率影响较小。

图7 变截面圆弧拱频率随高宽比变化关系

图8 正方形变截面圆弧拱的频率随外载荷倍数的变化关系

3.3 矩形变截面抛物线拱

图9 正方形变截面抛物线拱模型

(20)

其近似曲率半径表示为

(21)

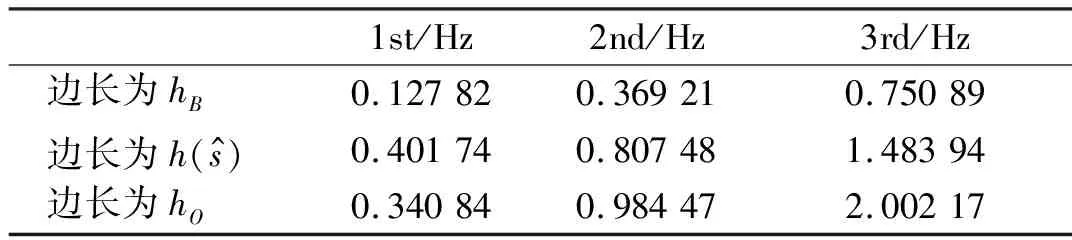
表3 两端固定正方形变截面抛物线拱面外弯扭振动的频率

图10 两端固定正方形变截面抛物线拱弯扭振型图

由表3可以看出，变截面抛物线拱的一阶频率比以边长为hO和边长为hB的等截面抛物线拱的频率都要大，而二、三阶频率则处于两者中间，这点与正方形变截面圆弧拱频率的变化规律基本一致，但是抛物线拱的所有频率数值均大于圆弧拱，振型图基本一致。

4 结 论

(1)通过等截面圆弧拱面外弯扭振动的数值计算结果和已有结果对比，说明绝对节点坐标法是一种很实用的动力学计算方法。

(2)正方形变截面圆弧拱面外弯扭振动振型的整体趋势与等截面圆弧拱基本一致，但是变截面圆弧拱的一阶频率比以左端、中间的正方形作为等截面圆弧拱的一阶频率都要大，而二阶、三阶频率则处于两者中间；变截面圆弧拱振动的频率分别随中心角、半径和高宽比增大而减小，并且他们改变对二、三阶频率影响较大，对一阶频率影响较小；均布径向载荷增大使得结构频率减小，其对二、三阶频率影响较小，对一阶频率影响较大。

(3)相同跨度和矢高的变截面抛物线拱与变截面圆弧拱的频率相差不大，其前三阶频率变化规律基本一致，振型图大致基本一致。