震损不规则装配框剪结构损伤评估
2021-08-11姜绍飞张漳荣
姜绍飞, 祝 豪, 张漳荣, 赵 剑, 王 耀
(1.福州大学 土木工程学院,福州 350108;2.中建海峡建设发展有限公司,福州 362000)
装配建筑因其生产效率高、节能环保而得到蓬勃发展。我国是一个地震多发国家,汶川地震、雅安地震[1]均造成大量结构损伤或破坏,而装配建筑的整体性能还略差于现浇整体式结构。为降低财产损失和方便后续结构加固,开展震后装配建筑快速评估显得至关重要。
黄超等[2]基于性能的抗震评估思想,以建筑结构的层间位移和构件塑性变形作为抗震性能评估的目标,从定量角度,基本上解决了目前既有RC建筑结构的整体抗震性能评估与加固处理问题;叶列平等[3]通过考虑建筑结构的抗震承载与塑性变形,提出了建筑结构抗震能力指标IS和需求指标IS0,并通过结合实际结构的震害强度,对它们的取值进行了确定;陈再现等[4]根据结构经过抗震性能试验后产生的裂缝位置、形状、宽度和长度评估结构的损伤程度;杜晓菊等[5]基于材料、构件损伤计算结构损伤指标D来评估结构的损伤程度;后来Park等[6]通过分析模态参与系数与层刚度损伤因子之间的关系,对环境激励下的建筑结构进行了损伤识别和评估。这些工作说明,选择某一性能指标(广义力或者位移)、结构固有特性(频率、阻尼比和模态参与系数等)或外观特性(裂缝、整体变形等),都可以评估结构损伤状态。
随着研究工作的深入,各国相继开展震后RC结构的鉴定评估标准的制订。如日本的《既有钢筋混凝土建筑抗震评估与加固标准》考虑构件塑性变形、结构抗震承载能力等因素,划分了三级抗震评估体系[7]。欧洲EC8[8]则是基于力和基于位移进行RC框架结构抗震性能评估,美国综合考虑建筑风险识别和抗震加固方法,我国也制订了相应的抗震鉴定与评估技术标准[9-10]。
虽然目前关于建筑结构抗震设计与评估的理论比较成熟,但对于(装配)结构的抗震性能评估存在诸多问题有待研究:① 损伤评估多集中在结构构件[11]、规则结构[12-13],且结构或构件基本为现浇式,而不规则、装配建筑震后评估未见报道;② 单一指标评估结构或构件偏差较大,如局部损伤较严重但整体损伤指标却无法较好反映真实状态;③ 量化的评估指标虽能指导现浇结构性能化设计,但对装配建筑的量化适用性不高。
据此,基于结构材料属性、层间变形、扭转变形及裂缝等参数,本文研究震损不规则装配框剪结构的综合损伤指标DI,建立DI限值与地震破坏水准之间的关系,其后用振动台试验和数值分析对所提评估理论的可行性和有效性进行了验证,并与脉动无损测试、规程评估结果进行了比较。
1 地震模拟振动台试验
1.1 试验概况
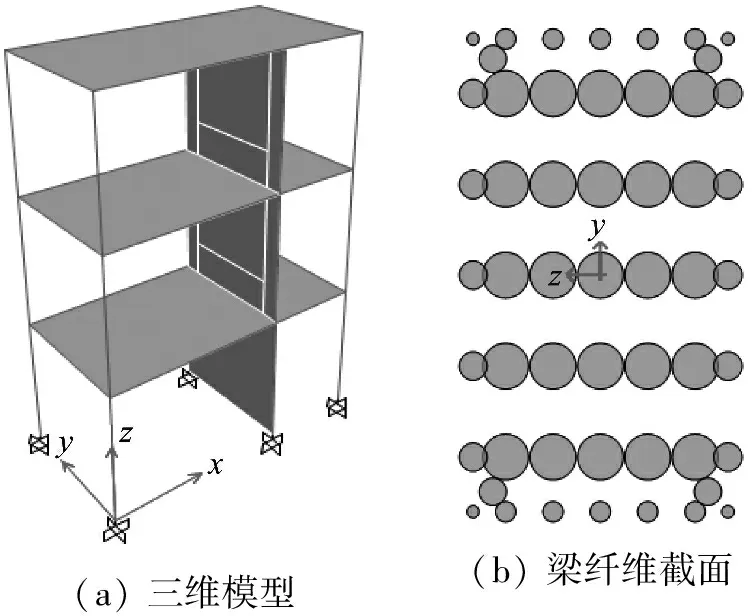
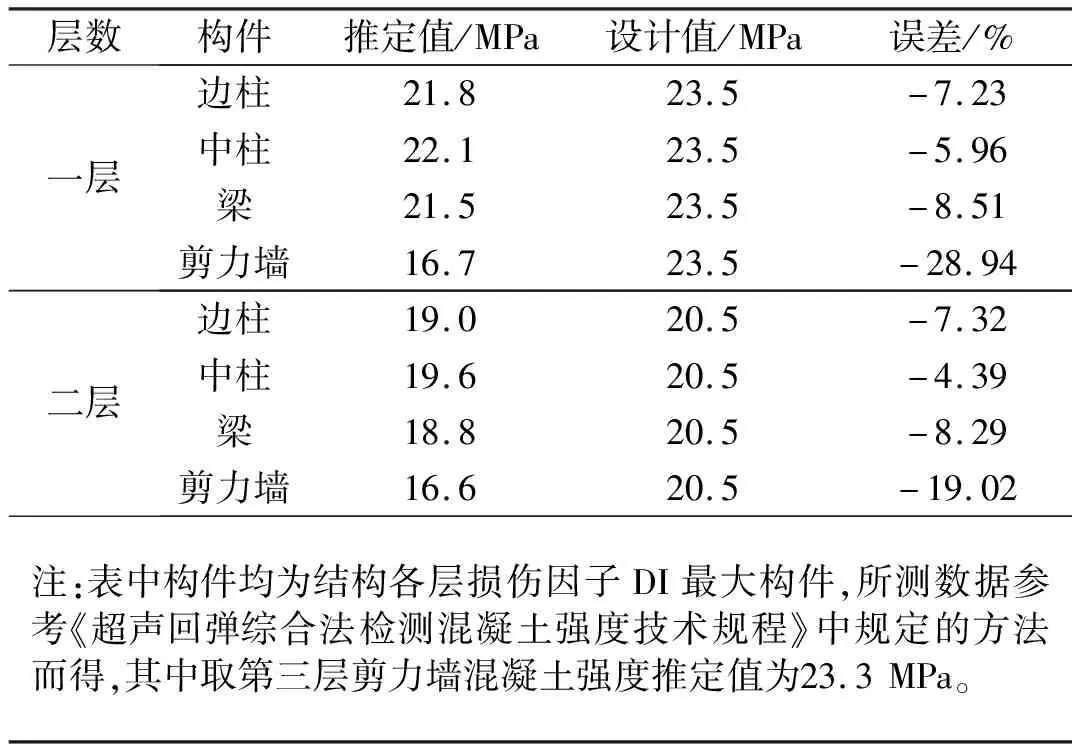
根据文献[14-15]、试验设备和场地,设计了一栋3层1/3缩尺RC不规则装配框剪模型(图1),其二、三层的剪力墙为干式连接(图2)。
主要设计参数如下:设防烈度为7度,设计基本地震加速度为0.15g,设计地震分组为第二组,抗震等级为二级,场地类别为Ⅱ类。结构平面尺寸为0.9 m×1.8 m,横向2跨(1.2 m+0.6 m),纵向1跨(0.9 m),层高均为1 m;梁、柱截面尺寸分别为75 mm×135 mm、100 mm×100 mm,剪力墙厚75 mm,楼板厚60 mm,梁、柱、剪力墙以及楼板的混凝土强度均为C30;箍筋为镀锌铁丝,梁箍筋为Ø3@50,柱箍筋为Ø3@60,梁柱纵筋均采用直径为6 mm的HPB300级钢筋;剪力墙采用双排双向受力分布筋Ø6@100;钢板为Q235且厚度为5 mm,螺栓为8.8级,连接钢框总长为660 mm;混凝土保护层厚度均为5 mm。相关材料参数见表1、2。

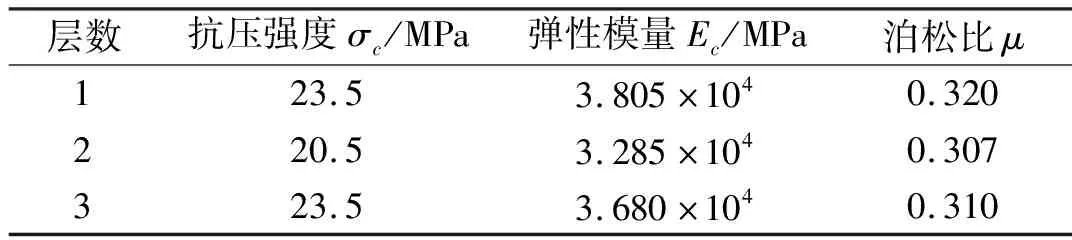
表1 混凝土材料参数
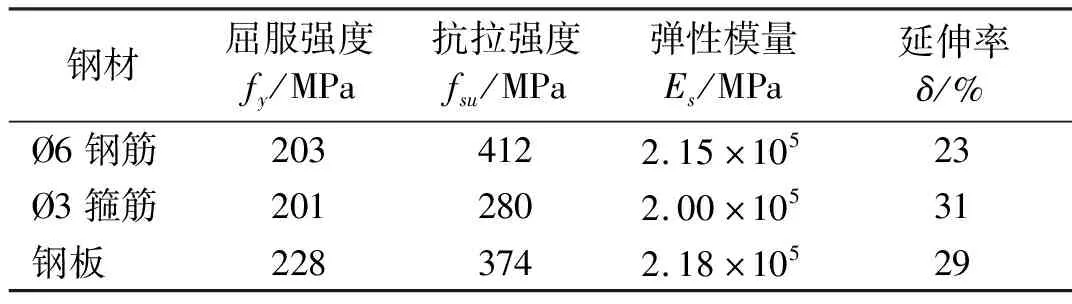
表2 钢材力学性能
选取El-Centro波、Taft波以及SHW2波作为地震动输入,沿结构横向施加地震动,对结构模型进行振动台试验。选取峰值地面加速度(PGA)作为强度度量参数,PGA取值为0.1g、0.15g、0.2g、0.31g、0.4g、0.51g和0.62g,其中SHW2波只加到0.51g。
1.2 变形分布
图3~图5给出了El-Centro波、Taft波和SHW2波作用下结构各层的层间位移,反映了整体结构的变形情况。当楼层变形超过结构本身的变形能力时,便发生破坏,层间变形的最大响应一般出现在结构受损较严重的部位即1~2层,它也反映了结构裂缝分布的主要规律。
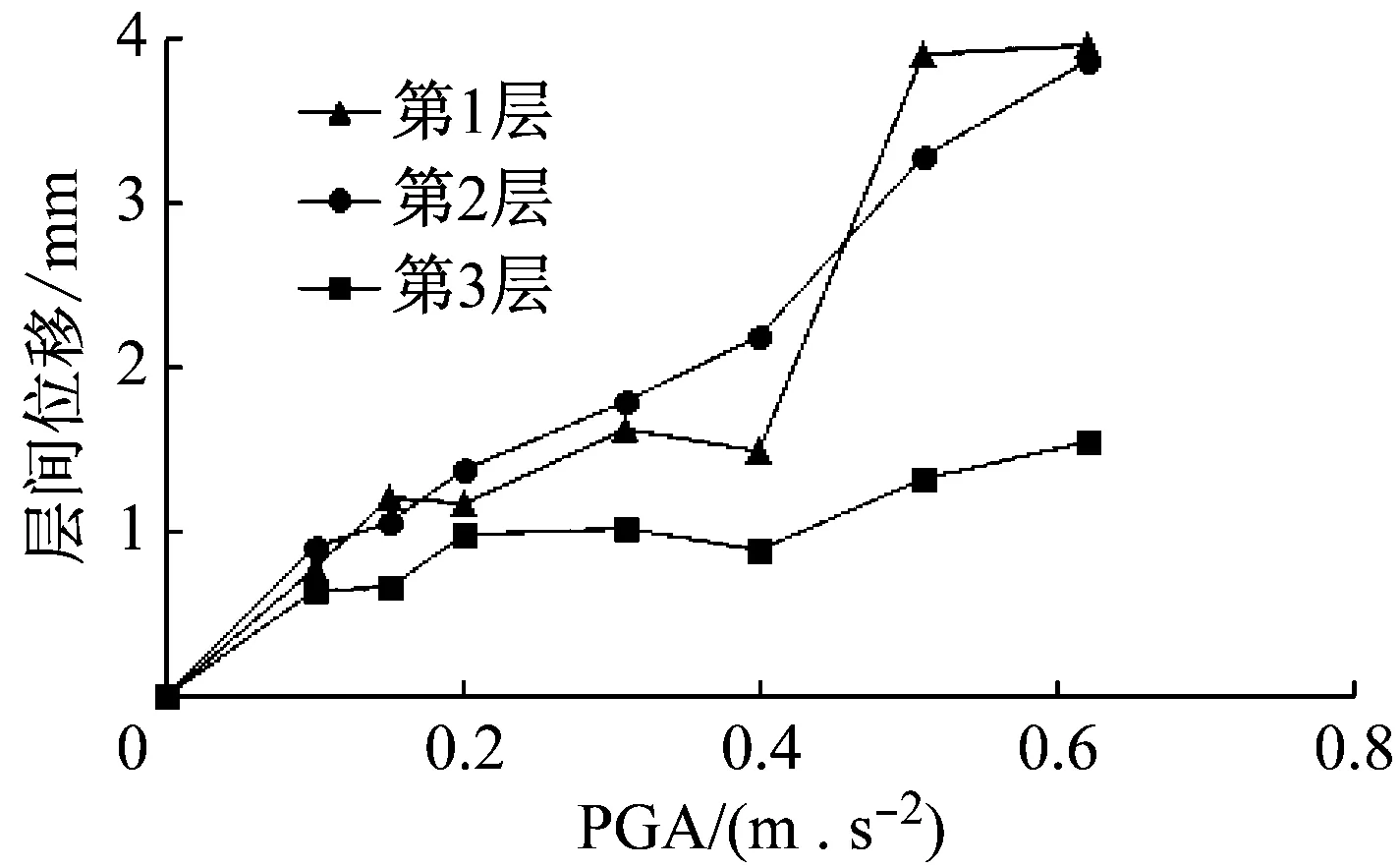
图3 El-Centro波作用下的层间位移
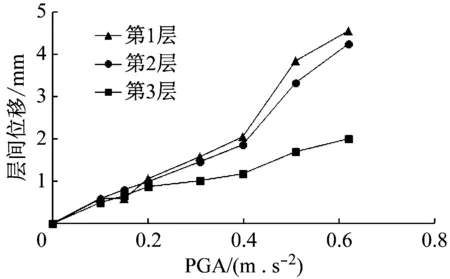
图4 Taft波作用下的层间位移
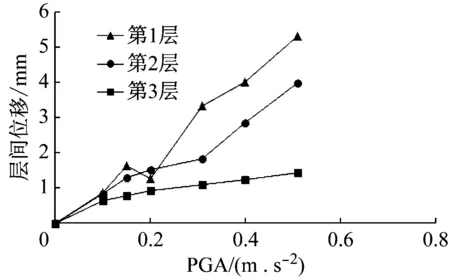
图5 SHW2波作用下的层间位移
图6~图8给出了三种波作用下结构各层的扭转角最大值。由于结构刚度分布不均匀,质量中心与刚度中心不重合导致结构发生扭转。几个图中都可看出,最大扭转变形出现在结构第2~3层,即不规则层,反映了结构平立面刚度分布的不规则性,增大了结构损伤程度。

图6 El-Centro波作用下的扭转角

图7 Taft波作用下的扭转角
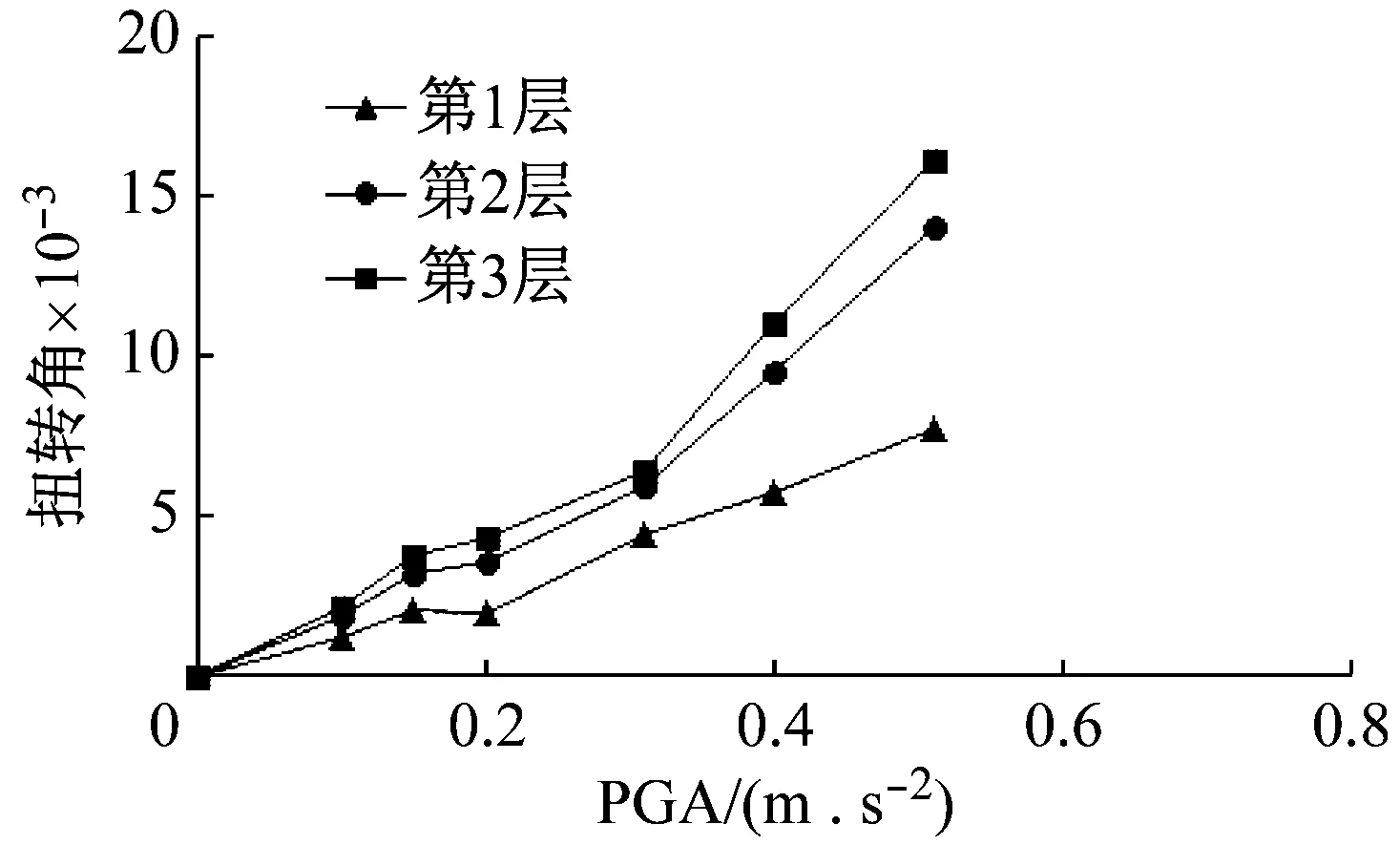
图8 SHW2波作用下的扭转角
1.3 裂缝分布
混凝土裂缝直观反映了结构的损伤情况,对结构进行裂缝检测,以保障其继续安全使用至关重要。
图9给出了不规则装配框剪结构裂缝分布图,测量其主要构件的25条裂缝,部分损伤较严重的列入表3,裂缝宽度及其数量如表4。

表4 裂缝宽度与其数量
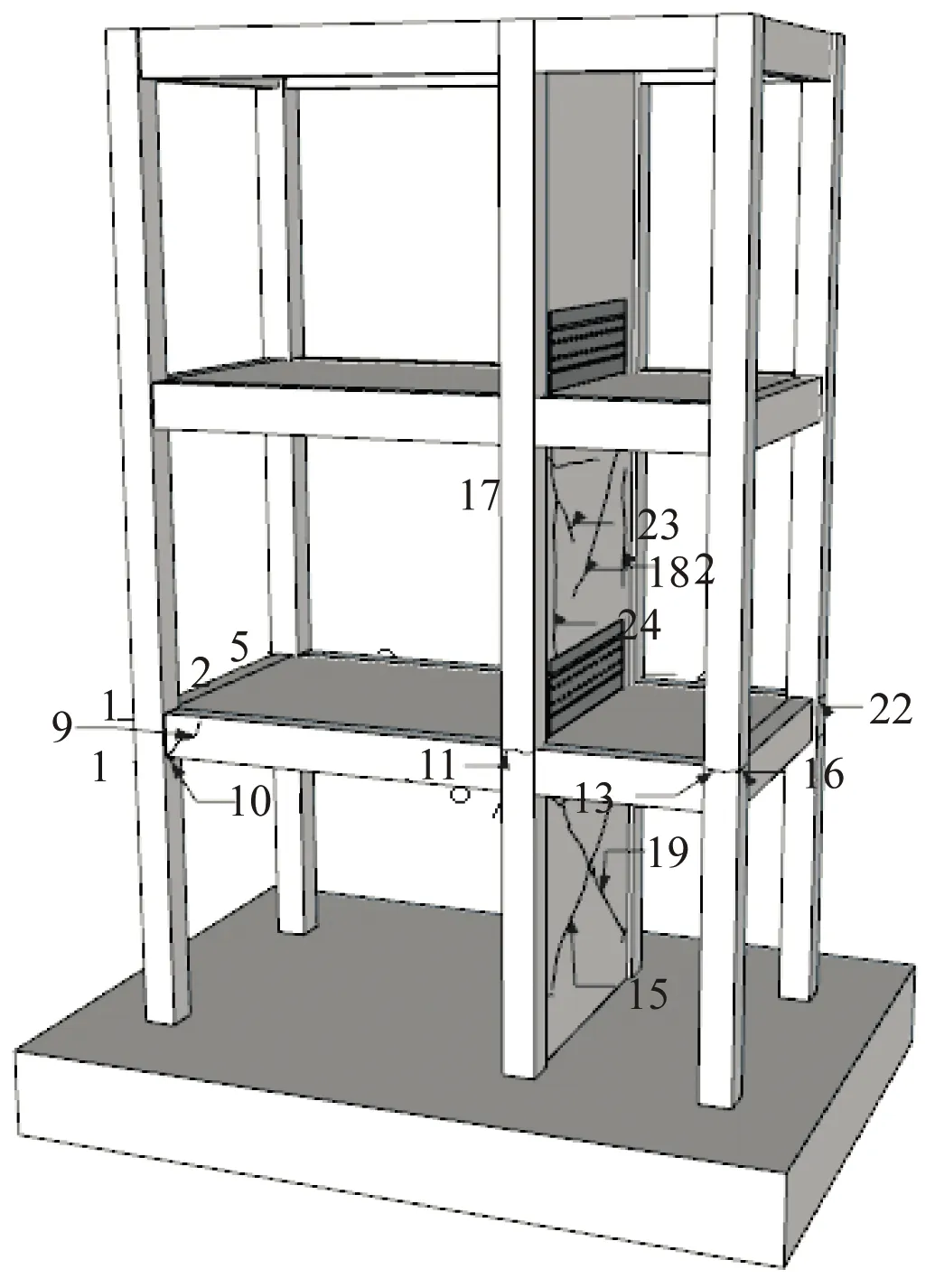
(a)三维立体图
损伤最严重几条未列入表 3:编号1贯穿梁端外沿,裂宽为0.861 mm;编号2孔洞缺陷较多,裂缝贯穿梁端外沿且柱端局部硂有脱落风险,裂宽为0.689 mm;编号5裂缝贯穿柱端表面外延,缝宽>1 mm且缝长接近100 mm,也可能为楼层拼接裂缝;编号22孔洞裂纹较多,裂缝贯穿梁柱相接部分。
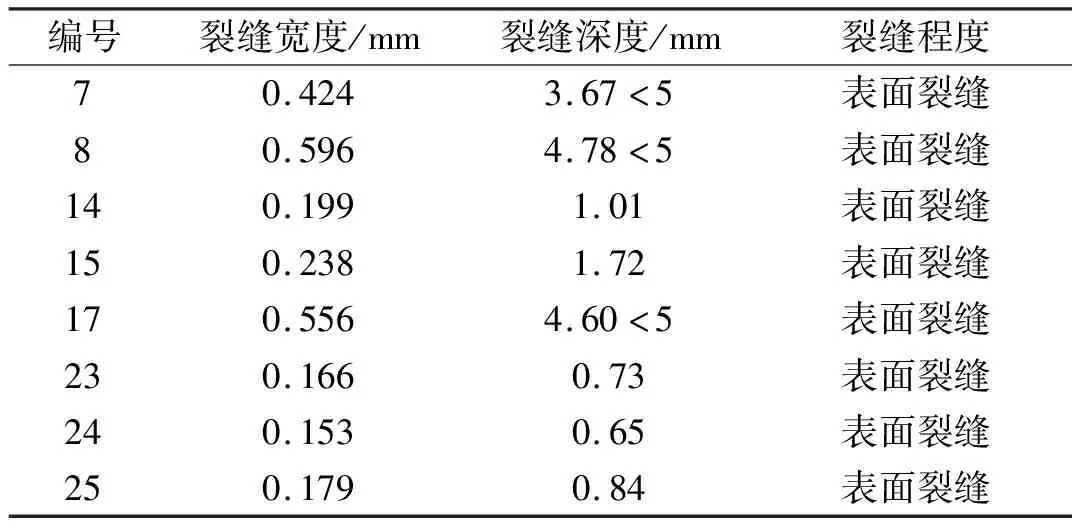
表3 主要构件裂缝
1.4 动力特性
地震损伤引发结构物理参数的改变,进而引起动力参数的变化,这里用动力参数的变化来评价结构状态。
(1)自振频率:它与结构质量和刚度相关,一般结构整体质量不会发生变化,故结构自振频率变化反映的是结构刚度的改变。由图10知,IAFSW结构前二阶频率变化趋势基本一致,其中震前结构前两阶频率分别为4.639 Hz、6.836 Hz,PGA=0.62g时下降为3.418 Hz、5.371 Hz,且随地震波PGA增大而下降幅度增大。说明结构出现累积损伤,整体刚度受到极大削弱。
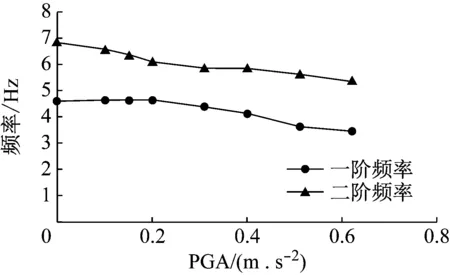
图10 不规则装配框剪结构频率变化
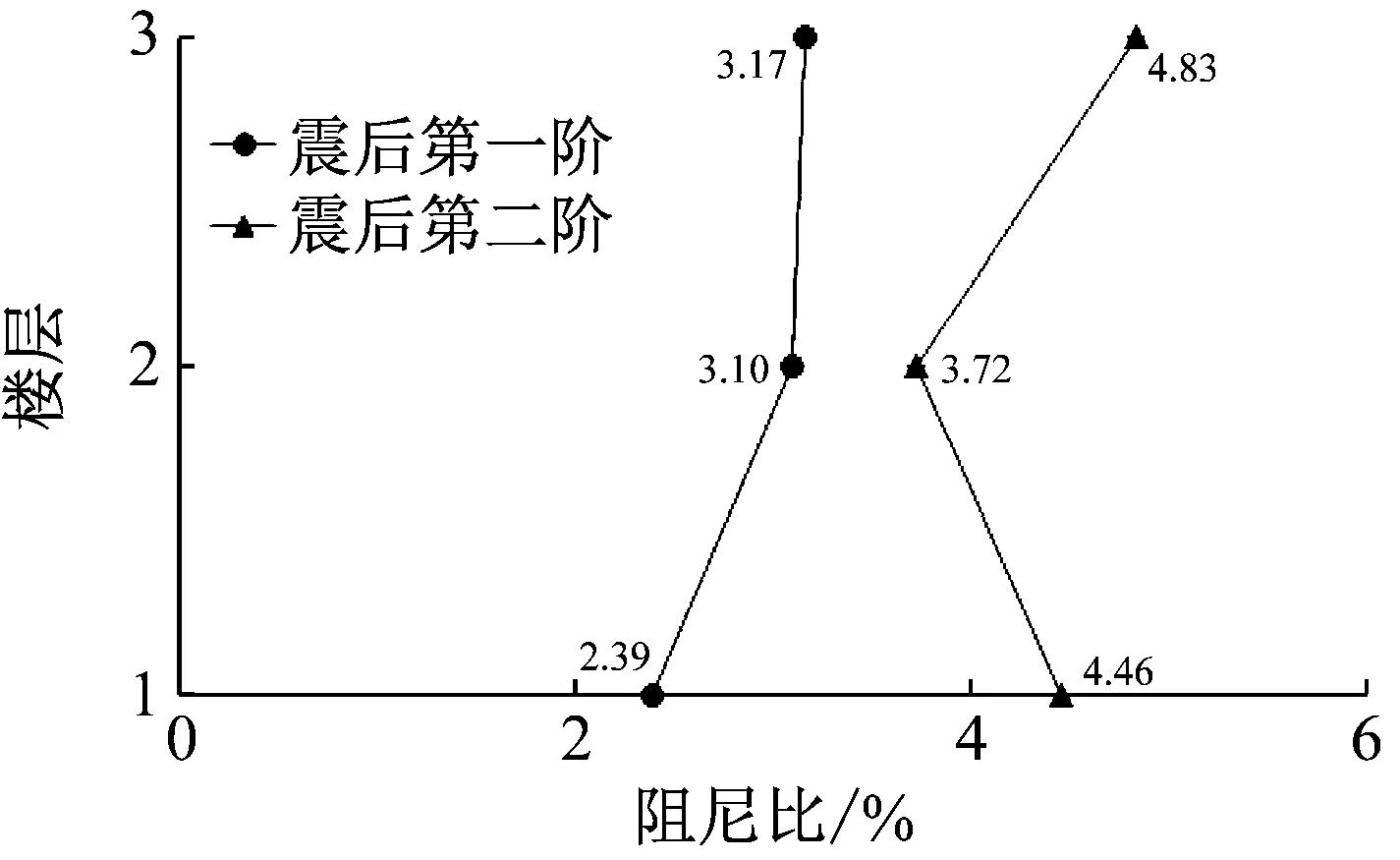
(2)阻尼比:它反映结构在振动过程中的耗能程度,阻尼比越大,耗能越大、结构损伤越轻微;当结构接近或进入弹塑性阶段后,阻尼比会随结构内力或变形的增加而迅速增大[16]。从图11的前2阶阻尼比看出,在PGA=0.2g前前2阶阻尼比基本一致,但PGA=0.51g前结构一阶阻尼比大于二阶阻尼比。
从振动形态看,结构一阶主要表现为横向平动,结构二阶表现为扭转变形;结构受到地震波PGA越大或越早进入弹塑性阶段,结构平扭耦合变形越明显,而一阶阻尼比突然大于二阶说明一阶阻尼对结构的平动耗能程度大于二阶阻尼对结构的扭转耗能程度。图11看出震前一二阶阻尼比为11.12%、12.35%,PGA=0.62g时提高到17.46%、16.31%,阻尼比均随地震波PGA增大而变大,说明结构阻尼对整体结构耗能越来越大。

图11 不规则装配框剪结构阻尼比变化
(3)振型:结构主振型与质量、刚度有关,随着地震波PGA增大结构损伤不断积累,结构质量基本不变而刚度变小。由图12知,弹性阶段,不规则装配框剪结构一阶振型呈弯剪变形形态,一、二层振型有逐渐外凸的迹象,整体变形形态由弯剪型向弯曲型过渡。由图知整体结构随地震波PGA增大而振型变化幅度较小,振型从反映了结构的相对刚度,说明低层结构振型对结构损伤影响较小。
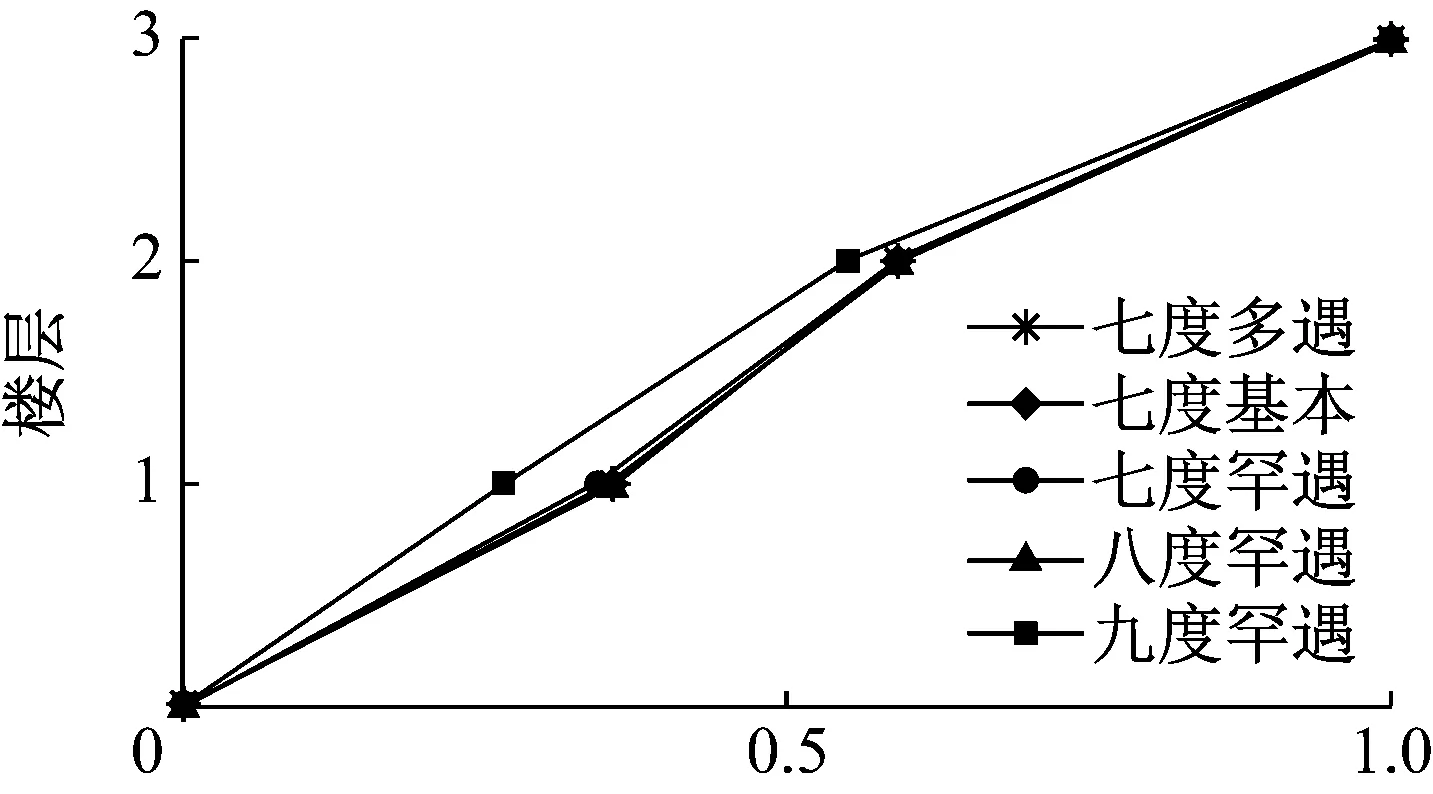
图12 不规则装配框剪结构一阶振型变化
2 震损不规则装配框剪结构损伤评估
2.1 现浇RC结构规程:层间最大位移角
按照现浇混凝土GB 50011—2010《建筑抗震设计规范》[14]规定,按照层间最大位移角限值(表5)对震损IAFSW结构进行损伤评估。

表5 不同破坏等级的层间最大位移角限值
由于IAFSW结构各层均为1 m,结合图3~图5的层间位移,可知层间最大位移角[θ]:①各楼层的层间最大位移角均小于抗规限制值0.02,满足“三水准”抗震设防要求;②各楼层最大层间位移角总的趋势是max([θ]1)≥max([θ]2)≥max([θ]3),在地震波不变的情况下,3层最大层间位移角与1、2层最大层间位移角差值随地震强度增加而增大,说明1、2层层间变形越来越大,3层层间变形相对很小;③图4中1、3层在0.51gPGA下的最大层间位移角以及图5中2层在0.31gPGA下的最大层间位移角变化较大。图4是由于1层抗侧刚度不及2层和3层的,结构扭转效应或弯剪变形突然加大;图5是局部构件中钢筋疲劳甚至屈服,提前进入弹塑性阶段或地震波频率与结构自振频率很接近。
除SHW2波作用下PGA=0.51g时,结构层间最大位移角为0.005 295 8>4[Δue]=0.005(层高1 m)外,其余层间最大位移角对应的结构破坏程度都在中等破坏或中等破坏以下。按最大损伤程度综合评估震损不规则装配框剪结构,应属中等破坏。
2.2 层间最大扭转角
由图13计算可得结构1~3层刚度中心的X向坐标:1.191 2 m、1.181 5 m、1.166 m,知结构楼层刚心不重合;另外计算楼层在El-Centro波、Taft波和SHW2波作用下的最大层间位移δmax均介于1.2倍~1.5倍的楼层两端最大层间位移的平均值(δ1+δ2)/2,两者的比值在Y向分别为:1.31、1.44和1.42,故本文研究结构为不规则结构。
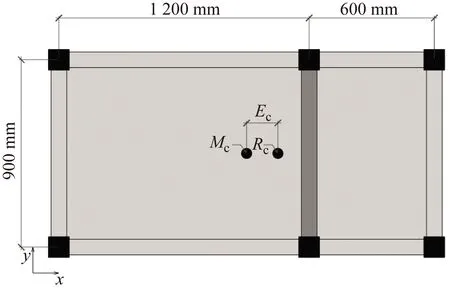
图13 结构平面不规则平面图
结构扭转角越大,结构扭动就越厉害,结构累积损伤效应也随之增加,扭转角亦是评估震损不规则结构的指标。这里采用广义层间扭转角θ/h来表征损伤[17]:
θ/h=(μ-1)[θ]/(μR)
(1)
式中:θ为结构的扭转角;h为结构层高;μ为扭转位移比,取值为1.2~1.5;[θ]为结构的层间位移角;R为构件到楼层转动中心的最大距离,假定结构刚度中心与转动中心重合。
广义层间扭转角θ/h限值可由层间最大位移角[θ]限值范围确定。由式(1)得震损结构1~3层的广义扭转角限值分别为2/815×10-3、2/753×10-3和1/665×10-3。
由图6~图8知,不规则装配框剪结构各层扭转角随PGA的增大而增大,最大扭转角都出现在三层,但每层的扭转角增长幅度却不一样,它随着楼层的增加而降低;与此同时,结构模型的扭转反应还和地震波的类型有较大关联,由于上海人工波强震时间长,所带来的地震冲击力更大,在PGA为0.4g时,SHW2波所引起的扭转反应明显要大于其他波。
根据图中数据除以层高h=1 m与上述限值比较,评定震损不规则装配框剪结构为严重破坏。
2.3 结构构件裂缝
裂缝可获得构件损伤情况。由GB 50011—2010《混凝土结构设计规范》[15]中结构构件最大缝宽限值和张坤[18]所述混凝土裂缝限值标准,知震损结构整体属轻微破坏。
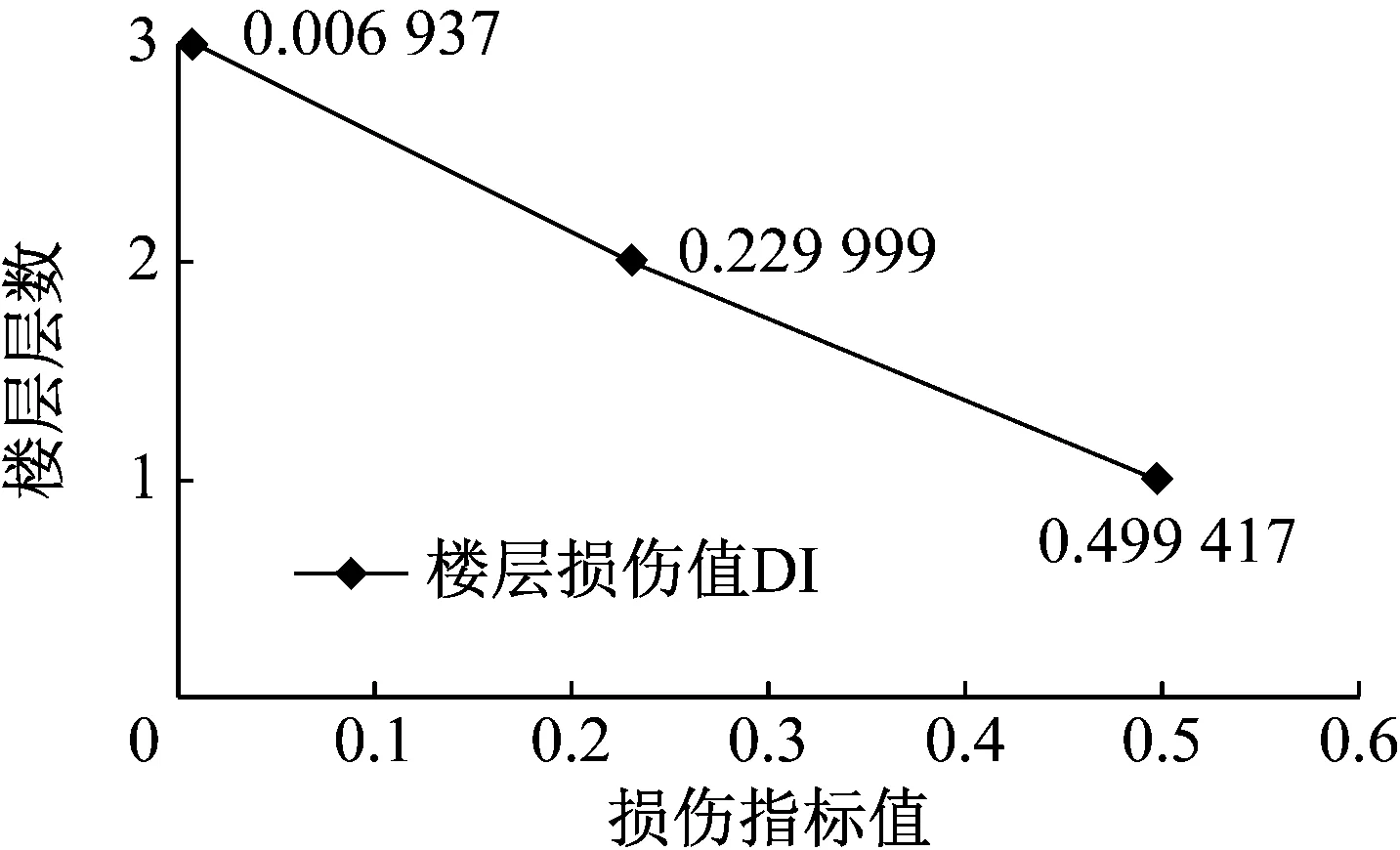
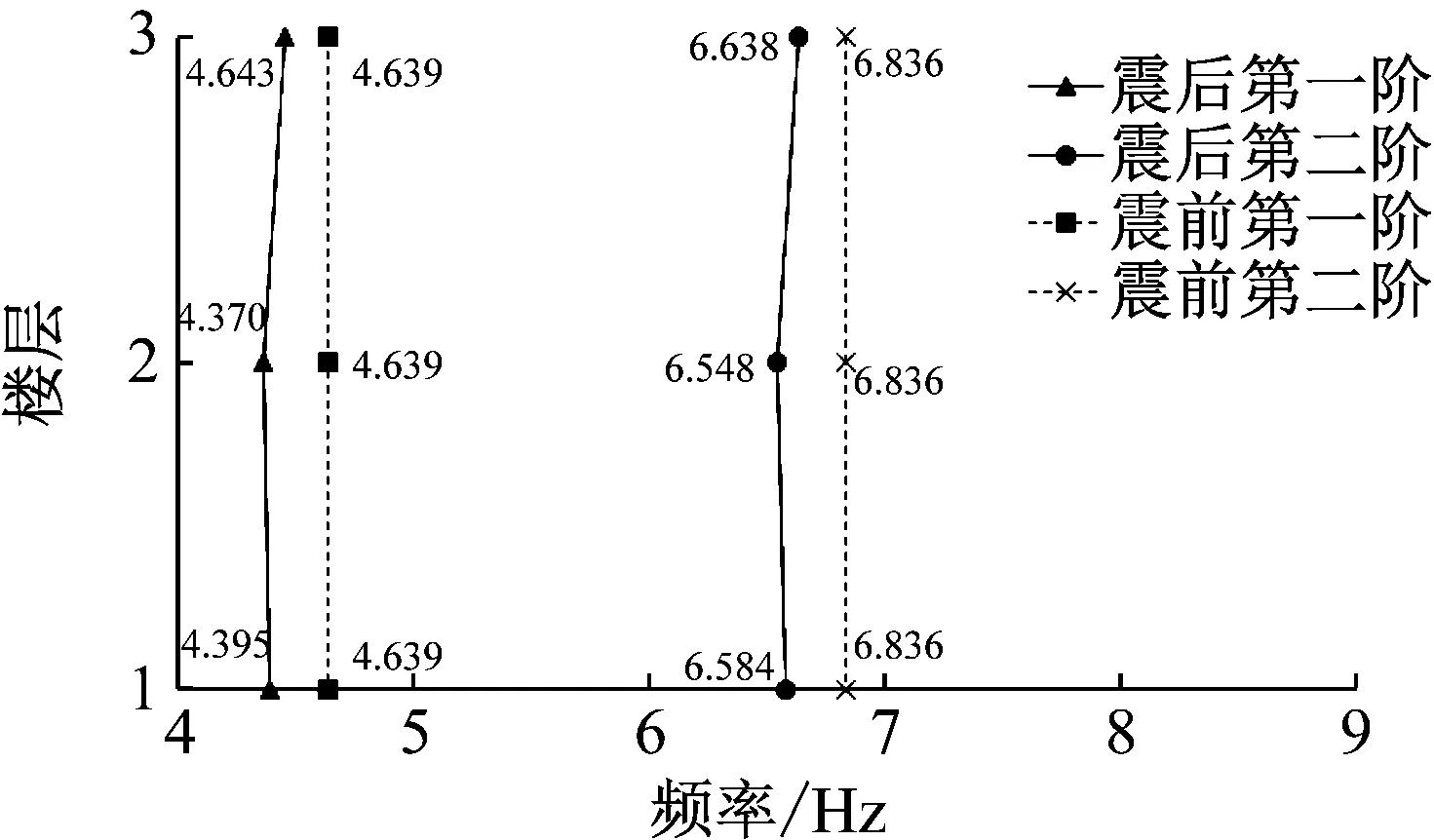
用单面平测法[19]测量结构构件裂缝深度。裂缝深度h与结构厚度H关系如下:h≤0.1H表面裂缝;0.1H 2.4.1 DI与结构性能等级 DI的范围为[0,1]:DI=0,完好状态;DI≥1,结构或构件完全破坏,DI值越大结构损伤越严重。DI能够反映从材料到构件截面、构件、楼层及结构多个层面[20],可精确评估震损不规则装配框剪结构的状态。 基于材料属性,通过加权系数得到初步的指标DI0,然后基于试验中的变形、裂缝分布等,对指标计算式中的系数修正,并依据文献[21]建立损伤指标限值DI与地震破坏水准之间的关系。DI计算过程如下。 DI0由混凝土和钢材损伤加权得到,其中混凝土纤维损伤量化采用双线性模型[22],见式(2)~(3),混凝土单轴本构为考虑箍筋约束作用的Mander模型[23]。 (2) (3) 式中:Dci为第i根混凝土纤维的损伤指标;Dcu为混凝土达到极限抗压强度时对应的损伤指标;σcd、σcu、σcf为混凝土棱柱体(150 mm×150 mm×450 mm)的初始破坏强度、极限抗压强度和残余强度,εcd、εcu、εcf为前述混凝土强度对应的应变。 钢筋、钢板和螺栓均属钢材,采用由CB 50010—2010《混凝土结构设计规范》[15]附录C中应力-应变本构模型,钢材纤维损伤量化采用式(4)来确定[24]。 (4) 式中:Dsi为第i根钢材纤维的损伤指标;(2Nf)j为第j周期下按塑性应变幅值加载至钢材断裂的半周期数。 震损不规则装配框剪结构的构件、楼层和结构体系的损伤指标值,均按式(5)计算: (5) 式中:λi为构件或楼层加权系数,λi修正为λi(1+λc+λd)。 构件加权系数除考虑材料外,还需考虑构件开裂影响,所以引入单个构件裂缝数量与结构总裂缝数量比值λc作为附加考量因子,由1.3节确定。楼层加权系数除使用构件损伤指标外,还应引入层间变形影响因子λd,来考虑薄弱层与损伤楼层位置的变化对结构的影响。 λd=λθ·λt (6) (7) (8) 式中:λθ为考虑层间最大位移的加权系数;λt为考虑层间最大扭转的加权系数。 根据GB 50011—2010《建筑抗震设计规范》[14],这里使用修正的DI对震损不规则装配框剪结构进行了损伤分析,将结构性能目标划分为五个等级,如表6所示。 表6 不同性能等级 2.4.2 结构损伤评估 图14和图15分别为震损不规则装配框剪结构的各个构件损伤值分布图、由构件损伤值加权组合得到的结构楼层损伤图,可以发现楼层越高结构损伤越轻,由式(5)得到结构损伤指标值DI=0.193 3,所以震损不规则装配框剪结构为中等破坏。 图14 震损IAFSW结构构件损伤指标值 图15 震损不规则装配框剪结构楼层损伤指标值 图16 结构有限元模型 上述有限元模型建立的过程中需要对材料本构模型修正。2.4.1小节的结构损伤指标DI考虑了结构材料最大的损伤程度,故可将其应用于混凝土材料和钢材,作为梁、柱、剪力墙中材料本构的影响因子。 对于混凝土材料的单轴本构修正,即将实测得到的混凝土结构构件强度(见表7)输入Mander曲线中并考虑损伤因子DI对本构参数的影响。其中结构模型第三层除剪力墙外,其余构件损伤不明显。 表7 结构构件混凝土强度 对于钢材的本构模型修正,因装配结构模型的损伤指标DI装配=0.193 3属中等破坏,而由戚永乐[11]给出的中等破坏限值知,纵筋的极限拉应变应取为εsu=0.05/0.6=0.083,结构震后Ø6钢筋的屈服强度fy装配=203×(1-0.193 3)=163.76 MPa,相应地抗拉强度ft装配=215.48 MPa,而钢筋的弹性模量Es装配根据各个构件的损伤程度确定。Ø3箍筋本构各个参数修正同Ø6钢筋。 3.2.1 无损脉动测试 用DH5920测试分析系统对震损IAFSW结构进行动力参数检测,布置x、y向各一个加速度传感器于如图17(a),测试结构2个方向振动加速度。 图17 现场动力测试震损装结构 使用DHDAS动态信号采集分析系统对IAFSW结构的加速度响应进行频谱分析,提取模态参数并分析频率、阻尼比和振型的变化,如图18~图20所示。 分析图18与1.4小节结构自振频率发现,(1)脉动法测试的不规则装配框剪结构震后自振频率小于前述1.4小节结构震前自振频率,但两者很接近,结构震后前2阶频率衰减程度均不超过6%,说明结构经地震作用后刚度退化,有真实损伤产生;(2)脉动法测试的结构自振频率明显大于结构在PGA=0.62g时的3.418 Hz和5.371 Hz。这里考虑到结构在震中受到的损伤是一个不断累积叠加的过程,持续受到强荷作用,而脉动法测试的条件是环境激励,结构受自然条件的影响,另外考虑到结构自身质量的影响,整体结构在震中的自身质量包含楼层的配重块质量,而脉动测试无楼层配重块质量,由(1)知结构是有真实损伤的,刚度存在退化,所以脉动法测试的结构自振频率大于PGA=0.62g时结构的自振频率。 传统的“食品添加剂”课程教学模式较为单一,多采用以教师为主的讲授式教学方法,机械性地将不同种类的食品添加剂分章节“满堂灌”,导致学生将“食品添加剂”简单理解为“食品化学”课程的延伸,无法真正理解食品添加剂在食品行业和日常生活中的作用,使得部分学生学习积极性不高、兴趣不浓厚。因此,传统的教学模式亟待革新突破以适应“食品添加剂”在新形势下的教学需求。 图18 结构震前后频率 分析图19与1.4小节结构阻尼比部分发现,而脉动法测试的不规则震损结构前两阶阻尼比小于结构震前阻尼比和结构在PGA=0.62g时的前两阶阻尼比17.46%和16.31%,原因是脉动法测试与后两者测试的条件不同,前者是自然条件下的阻尼比而后两者受地震波(白噪声和其它波)作用,另外结构阻尼比大小反映着结构耗能程度,在自然条件下结构耗能明显小于在地震波作用下的结构耗能。 图19 结构震后阻尼比 由图20和1.4小节的图12知,IAFSW结构震后一阶振型第一层增大8.73%、第二层增大26.12%,线型外凸,几乎呈线性。在此过程中,结构变形形态由弯剪型向弯曲型过渡,说明振型的变化与结构变形形态有关,从而对结构损伤有影响。 图20 结构震前后一阶振型 由图18~图20知,考虑频率、阻尼比和振型的影响,结构震后损伤增大,一二层损伤较第三层明显。 3.2.2 有限元验证 为保证有限元模型能够可靠地反映前述结构的真实损伤,和为了能够更好地且有效地保证参数设置的准确性,本小节对修正后的有限元损伤模型进行了模态分析,模态参数亦是检查模型是否正确建立的标志之一。将白噪声、有限元程序和脉动法对应的频率分别记为f白、f有和f脉,误差记为e1=|f有-f白|/f白,e2=|f有-f脉|/f脉。 由表8知,不规则装配框剪结构震前在有限元程序里面的一二阶频率与试验时白噪声所得频率分别相差1.23%和0.57%,震后在有限元程序里面的一二阶频率与脉动法所测频率分别相差5.15%和0.87%,上述比例均不超过6%,说明结构模态周期匹配良好。 表8 结构模型模态频率 由图21知,IAFSW结构震前在有限元程序里面的一阶振型第一、二层的振型数值与试验时白噪声所得数值分别相差0.02%和7.64%,震后在有限元程序里面的一阶振型第一、二层的振型数值与脉动法所测数值分别相差3.63%和1.15%,上述比例均不超过5%,说明结构振型匹配良好。 图21 结构模型一阶振型 结构模型的阻尼比在程序中默认为0.05,经分析装配框-剪结构模型震后一二阶阻尼均比为0.050 2,可发现,结构震后阻尼比会返回至接近最初状态的值。 综上所述,结构模拟效果较好,说明有限元损伤模型中的参数设置合理,可用于相关后续的分析工作。 采用“全面分析、综合判断”的原则可快速掌握震损结构的整体破坏状态和薄弱环节,如表9所示。 脉动法评估指标由式(9)确定,该指标基于刘成清等[25-26]提出的考虑高阶振型、振型参与系数、结构自振频率、阻尼比等影响因素的损伤模型,本文对其损伤指标进行了修正。 (9) 由式(9)计算得D试验=0.593 4;D脉动=0.443 3,两者均介于0.4~0.6之间[26],脉动法评估结果与1.4节试验评估结果一致,不规则装配框剪结构属中等破坏。 由表9知,震损IAFSW结构由试验结果直接取层间最大扭转角、层间最大位移角和结构动力特性等指标评价时,震损结构分别为严重破坏、中等破坏和中等破坏;采取测量手段使用裂缝参数评价震损结构时,震损结构表现为轻微破坏,表明结构局部损伤并不严重;而使用修正的结构损伤指标DI评价震损结构时结构表现为中等破坏,这与无损脉动法、规范层间最大位移评估结果一致。由此可知,震损IAFSW结构评估为中等破坏才符合实际状态,即DI能精确评估震损结构。 表9 无损指标评估 (1)提出了不规则装配建筑损伤指标DI,并对指标计算式中相关参数进行了修正,该指标考虑了结构材料属性、层间变形、扭转变形以及裂缝参数等影响,此外,还建立了该指标DI限值与地震破坏水准之间的关系,对震后结构破坏程度的整体快速评估和局部薄弱环节的识别具有重要意义。 (2)使用振动台试验案例和有限元分析对所提结构综合损伤指标DI进行了验证。结果发现,结构综合损伤指标DI相对层间最大扭转角、裂缝等更能真实反映震损结构损伤情况,而且与基于脉动法的结构整体损伤检测评估和规范层间最大位移评估结果一致,说明结构综合损伤指标DI用于评估装配震损结构是可行的。 本文初步验证了结构震害级别与所提评估指标之间的对应关系,但还需更多的试验或仿真来进一步验证相关理论。上述工作为装配混凝土结构损伤评估、震损结构剩余使用寿命预测以及加固提供技术参考。2.4 综合损伤指标DI

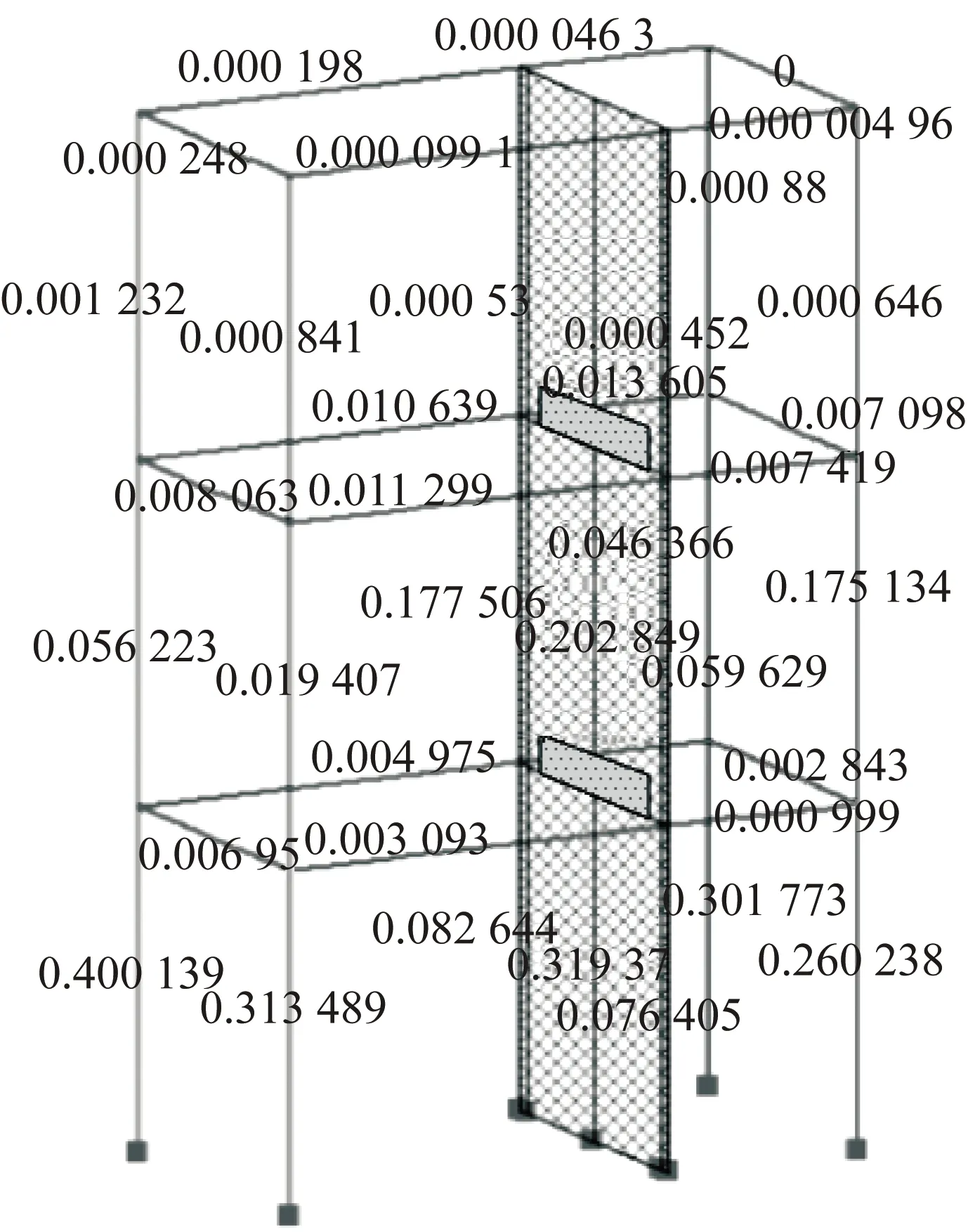
3 IAFSW结构损伤模型与验证
3.1 IAFSW结构的损伤模型
3.2 模型有效性验证

3.3 比较与讨论

4 结 论
