基于区域PMU和节点故障注入电流的广域后备保护算法

童晓阳，张生鹏，2，张广骁

（1.西南交通大学电气工程学院，四川省成都市 610031；2.国网阜宁县供电公司，江苏省盐城市 224400）

0 引言

随着电力系统的发展，电网结构日益复杂，基于本地信号的传统后备保护整定变得困难［1-3］。相量测量单元（PMU）由于时间精度高、测量结果准确等优点，成为输电线路故障检测和定位的新手段［4］。考虑PMU的经济性，需要研究基于一定数量PMU的输电线路广域后备保护算法，在信息不全的条件下进行检测，比传统后备保护更快地检测出线路故障。

文献［5］提出了基于电压故障分量和功率分布的后备保护方案；文献［6］通过比较疑似故障线路两端正序电流相角绝对值检测故障线路；文献［7］采用多源数据融合法判断故障线路；文献［8］采用阻抗矩阵，利用一个区域内同步或非同步PMU信号，以负序故障分量构造线性方程，通过残差判断故障线路。文献［5-8］均需要全局布置PMU，成本较高。文献［9-10］仅利用同步电压相量进行故障定位，只需要配置少量PMU，但需要进行遍历搜索，算法较为复杂且不能满足全局可观性。文献［11］提出间隔母线布置PMU策略，是一种可满足全局可观性、故障可定位的PMU最优布点策略。文献［12］利用S变换构造时频矩阵，利用奇异值分解剔除冗余信息，对时频矩阵与样本库矩阵计算矩阵相似度，从而识别区内外故障。文献［13-14］从故障电阻为纯电阻角度构造测距方程，准确求出故障点位置，但计算过程复杂。

本文考虑负载电流对节点注入电流的影响，基于间隔母线布置PMU，先确定故障区域，估计故障区域中未布置PMU母线的电压和节点注入电流，由故障前后的节点电压方程推导出节点电压故障分量方程，构造节点故障注入电流相量，分析其在故障前后的变化特征，构造广域后备保护判据。最后，利用电磁暂态软件PSCAD/EMTDC搭建了IEEE 39节点系统仿真模型，在各种故障场景下对所提广域后备保护算法进行了验证，结果表明所提方法不受故障位置、类型和过渡电阻影响。

1 基于节点故障注入电流的线路故障检测

设线路i-j上f点 发生故障，如 图1所示。f与节点i之间距离占线路i-j全长的比例为x，线路i-j的阻抗为Zij。

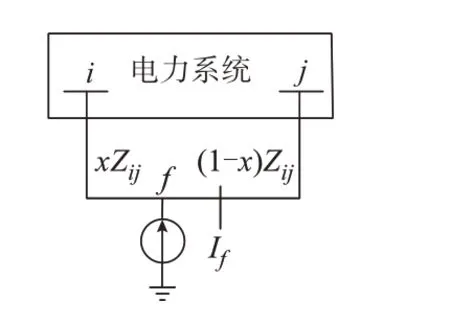
图1 线路故障示意图Fig.1 Schematic diagram of line with fault

基于节点电压方程思路［7］，考虑各节点注入电流，对于一个区域中节点数为n的电网，列出故障发生前该区域的节点电压方程为:

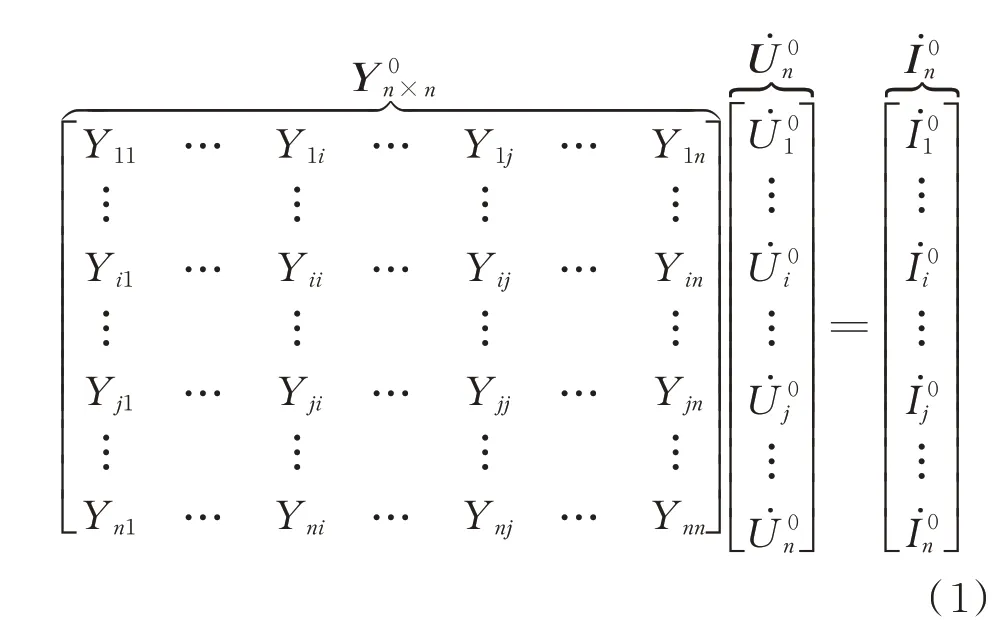
2 区域中节点电压与节点注入电流估计

在保证所有发电机节点都布置PMU的基础上，间隔母线布置PMU，将与未布置PMU母线直接相连的所有已布置PMU母线所形成的包络区域作为一个典型保护区域。

区域Z包含n+1个母线节点，除中间母线M未布置PMU外，其余母线均布置了PMU，见图2。

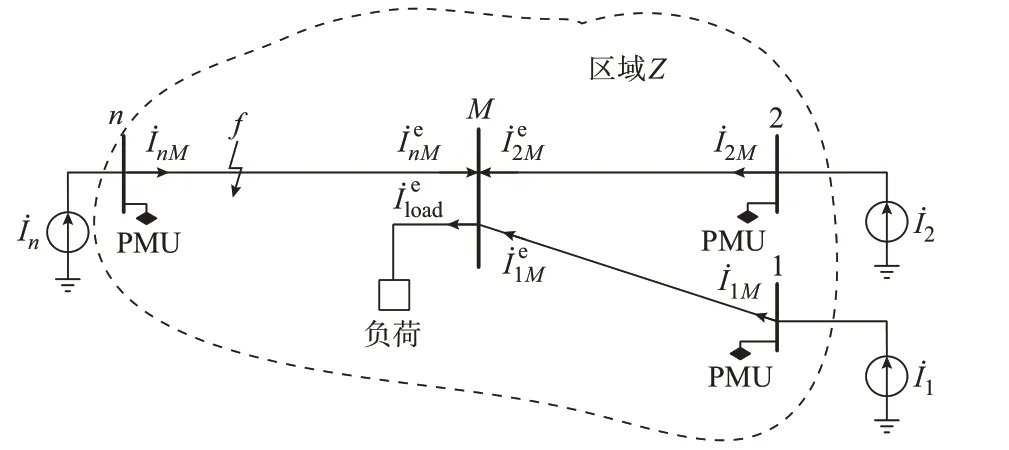
图2 间隔母线布置PMU的典型区域示意图Fig.2 Schematic diagram of typical area with PMUs spaced apart

由式（18）可知，对该区域应用节点电压故障分量方程求取İdn，必须先获得各节点的注入电流和节点电压。由于正序分量存在于各种故障类型中，故本文均采用正序分量进行计算。图2中规定流向母线的节点电流为注入电流正方向，İi(1≤i≤n)为布置有PMU节点的等效注入电流。

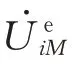
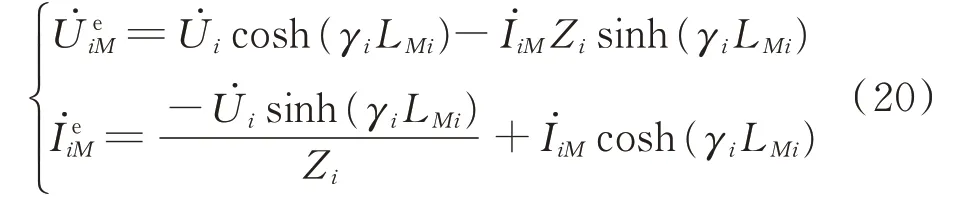
式中:γi为线路M-i的传播系数；Zi为线路M-i的特征 阻 抗；LMi为 线 路M-i全 长；İiM为 线 路i-M的i侧电流。

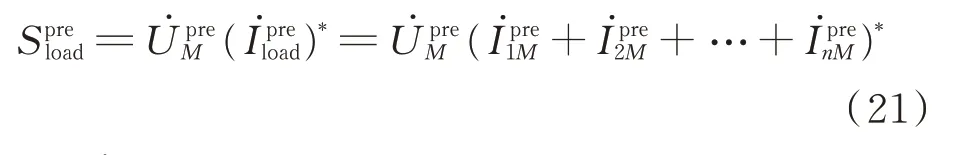
当线路M-N正常时，来自n个PMU的各正序推算电压幅值理论上相等。当线路M-N发生故障后，对于一般性多数故障情景如金属性接地故障、相间故障等，来自故障线路PMU侧（如N侧）的正序推算电压的幅值要明显小于来自正常线路PMU侧的各推算电压幅值。因此，在估计母线M电压时需要舍弃来自故障线路侧的正序推算电压。对于近末端高阻故障情形，来自故障线路侧的推算电压可能与来自某相邻正常线路的推算电压的幅值差异不大，这时，舍弃的幅值最小的推算电压可能不是来自故障线路侧的推算电压，但是它们比较接近，用式（22）计算的母线M的估计电压仍然相对准确。

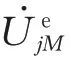
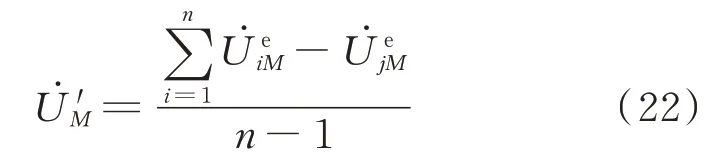
文献［15］利用动态加权因子求取未布PMU母线的估计电压，因为考虑了故障侧的推算电压，母线的估计电压的求取并不太准确。

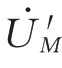
根据传统电力系统潮流计算原理，对整个系统列写节点电压方程，某节点的注入电流就是发电机注入电流减去负载电流。

本文对电力系统中边界布置有PMU区域，在列写节点电压方程时，节点注入电流的定义有所不同，即区域内母线i的节点注入电流除了发电机注入电流减去负载电流外，还需要加上区域外与母线i相连线路注入母线i的电流之和。根据电路理论中的替代定理，将区域外与母线i相连各线路流向母线i的电流和替换成一个等值的电流源İk，i。

区域内母线节点注入电流示意图如附录A图A1所示，节点i的注入电流表达式为:

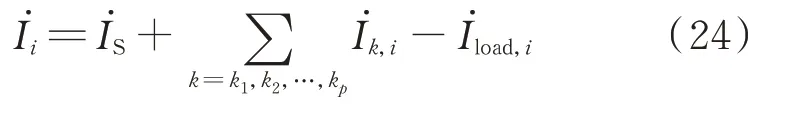
式 中:İS为 发 电 机 向 母 线i注 入 的 电 流；İload，i为 母 线i的 负 载 电 流；İk，i为 区 域Z外 线 路k流 向 母 线i的 电 流相量，k1，k2，…，kp对应与区内母线i相连各线路对侧的区外母线。

对于图2区域Z中布置有PMU的母线i，其节点注入电流由式（24）得到。需要指出，式（24）为节点注入电流的一般表达式，并非所有布置有PMU母线的等效注入电流均由这3部分组成，有的布置有PMU母线的节点注入电流只包含其中一部分或两部分。例如:当母线i仅与发电机相连时，等效注入电流就等于发电机注入电流İS；当母线i仅与区域外线路相连时，等效注入电流只包括İk，i。当母线i与区域外线路相连且接有负载时，等效注入电流包括İk，i和İload，i两 部 分。因 此，需 要 根 据 具 体 情 况 应 用式（24）。

对于图2中未布置有PMU的母线M，没有区域外线路和发电机与其相连，母线M的节点注入电流只有负载电流，这时可用式（23）求出该节点的负载电流，母线M的节点注入电流为负载电流的负值。如果母线M没有负载，其节点注入电流为零。

将区域内各节点故障后等效注入电流减去故障前等效注入电流，得到等效注入电流故障分量列向量Δİ。区域内各线路参数及拓扑均为已知量，求得区域内各节点的电压故障分量、等效注入电流故障分量后，由式（19）得到节点故障注入电流。

3 基于节点故障注入电流的广域后备保护

3.1 子站启动判据和故障区域的搜索

为了减少广域保护系统的通信量和计算量，一般根据相关算法筛选故障区域。本文采用广域电流差动原理来确定故障区域，引入文献［16］确定故障关联域的保护判据。调度中心通过广域通信网络实时收集每个区域的各边界节点的正序电流，计算每个区域的所有边界节点的电流相量和的幅值为Itotal，如果某个区域的Itotal大于设定阈值，就判断该区域为故障区域，判据如下:

式中:Iset为区域内因负荷电流、线路的分布电容电流而额外产生的注入电流启动阈值，其值设定为电网正常时一个区域的所有边界节点的电流相量和幅值乘以一个系数，该系数为1.3～1.5。

在确定故障区域后，再采用本文提出的基于节点故障注入电流的算法来检测故障线路。

3.2 保护动作判据

由第1章可知，线路发生故障时，故障线路两端的 节 点 故 障 注 入 电 流 分 别 为(1−x)İf、xİf。它 们 与故障点位置x呈比例关系，而其他正常线路两端的节点故障注入电流理论上为零，利用它们之间的比值，可自适应检测故障线路。

考虑到计算、测量、估计等环节误差的影响，正常节点的节点故障注入电流不可能完全等于零。在计算得到区域内各节点的节点故障注入电流后，将所有故障注入电流按照幅值进行排序。定义K为节点故障注入电流幅值最大值与第三大值的比值。

如果检测到存在连续的3个K满足K＞Kset，则判断İdn中元素最大值和次大值对应的线路为故障线路，Kset为设定阈值。

电网正常运行时某区域中所有节点故障注入电流的比值约为1，考虑测量误差、计算误差等，乘以可靠系数（1.5～3），对于估计误差，再乘以一个可靠系数（2～3），故设置Kset=10。

3.3 算法步骤

步骤1:对整个电网进行区域划分，按照间隔母线布置PMU策略，调度中心或区域控制主站通过广域通信网络实时收集各区域中各PMU的电压、电流，计算各区域的所有边界节点的电流相量和的幅值Itotal，如果某区域的Itotal大于Iset，就判断该区域为故障区域，此时广域保护启动。

步骤2:针对故障区域，收集保护启动后该区域中每个PMU在各采样时刻的电压、电流。

分别计算故障区域的各节点电压故障分量ΔU̇、节点注入电流故障分量Δİ，通过式（19）计算得到故障区域各节点的故障注入电流İdn。

步骤3:对İdn中各电流幅值排序，计算得到K，如果K大于Kset，则记录超过1次。当K连续超过阈值3次，则判断İdn中最大值和次大值对应线路为故障线路，否则，返回步骤2。

所提算法的流程图如附录A图A2所示。

4 仿真验证

4.1 仿真模型

利用电磁暂态仿真软件PSCAD/EMTDC搭建IEEE 10机39节点系统，系统结构如图3所示。

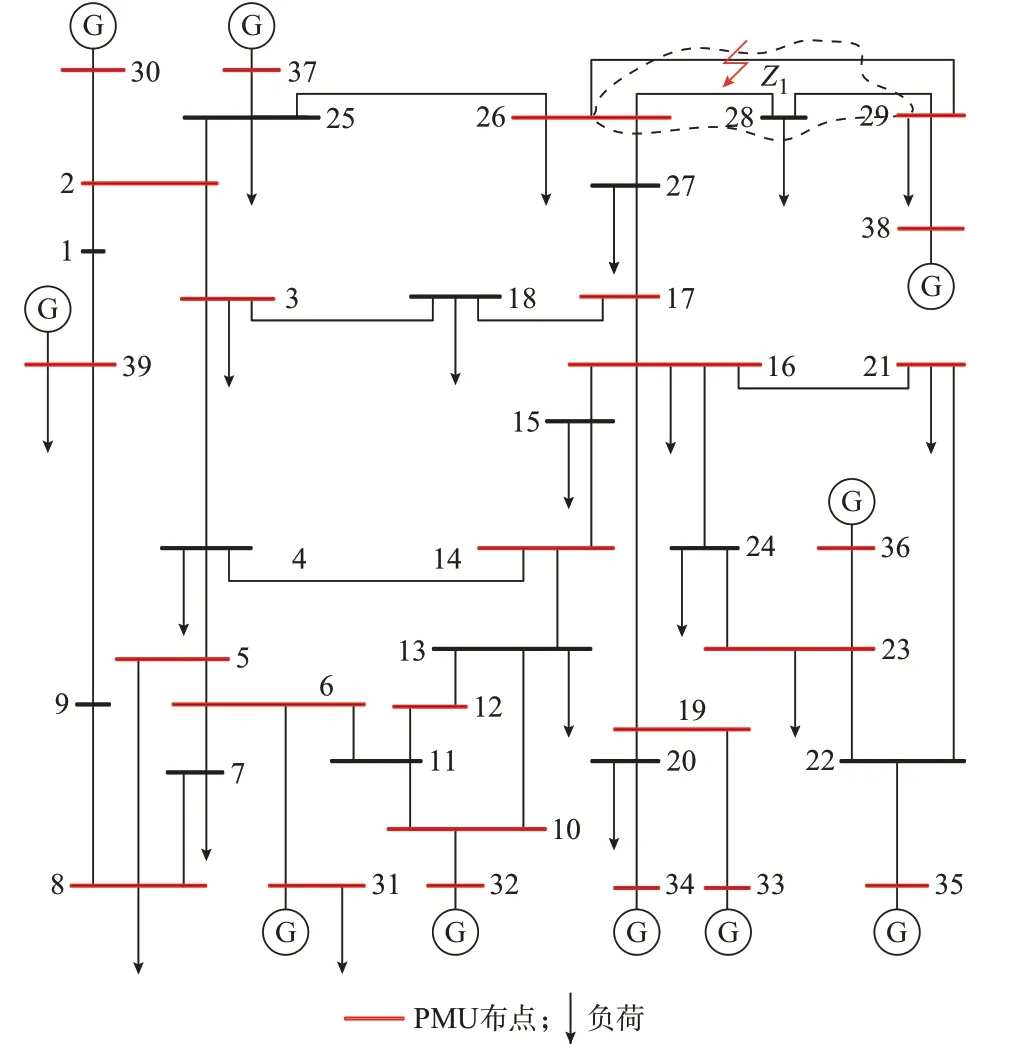
图3 IEEE 39节点测试系统Fig.3 IEEE 39-bus test system

图3中红色母线表示安装PMU，系统电压等级为345 kV，频率为60 Hz，采样频率为3 kHz。系统中各母线的负荷设置为恒功率模型。

4.2 算例分析

4.2.1各种故障情景的仿真结果

为了验证故障点位置、故障类型和过渡电阻对本算法的影响，设置区域Z1中的线路26-29发生故障。故障分别在距离母线26的5%、50%、95%处，故障类型有A相接地（AG）、AB相间接地短路（ABG）、AB相间短路（AB）、ABC三相短路（ABC）故障，对于接地故障设置300Ω过渡电阻。其中，区域Z1中母线26、29布置PMU，母线28未布置PMU。

线路26-29发生各种故障时各节点故障注入电流的仿真结果如表1所示。其中，数据均取自故障后1个周期之后的稳态值；Id26、Id28、Id29分别表示母线26、28、29的节点故障注入电流幅值。

表1 区域Z1中线路26-29发生各种故障的仿真结果Table 1 Simulation results of various faults on line 26-29 in zone Z1

由表1看到，在线路26-29发生各种故障时，其两侧的节点故障注入电流Id26、Id29总是区域中节点故障注入电流的最大值和次大值，且最大值是第三大值Id28的10倍以上，即正常节点的节点故障注入电流始终远小于最大值。本方法能够准确检测故障线路26-29，不会对区域内的正常线路误判。

当线路26-29于0.3 s在距离母线26的50%处发生A相金属性接地故障时，各节点的电压故障分量和节点故障注入电流波形如附录A图A3所示，对应的各节点故障注入电流幅值见附录A图A4。由图A4可见，在0.3 s发生故障后，故障节点注入电流幅值Id26、Id29迅速增大且近似相等，正常节点28的故障注入电流幅值Id28保持接近于0，与理论符合。

故障后约1个周期，节点26、28、29的电压故障分 量 稳 定 值 分 别 为14.304 4∠−83.551 6°、6.245 3∠−83.566 1°、3.644 3∠−86.528 2° kV，节点 故 障 注 入 电 流 分别为0.899 8∠−167.826 2°、0.021 6∠−82.740 9°、0.892 2∠−175.566 3° kA。故障节点26、29的故障注入电流幅值分别为0.899 8、0.892 2 kA，二者近似相等，正常节点28的故障注入电流幅值为0.021 6 kA，不会因为区外故障而增大。

此时K的变化曲线如图4所示。由图4可见，0.3 s发生故障约1个周期之后，比值K较平稳，且远大于阈值，可准确检测出故障线路26-29。

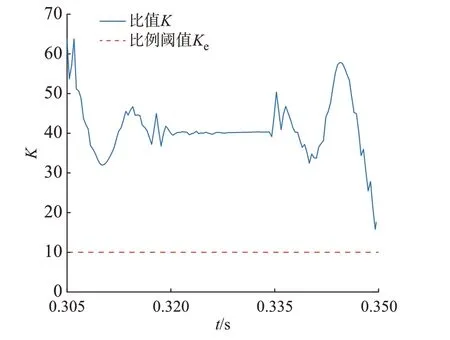
图4 线路26-29在50%处发生AG故障时K值曲线Fig.4 Curve of K with AG fault at 50% of line 26-29

4.2.2非全相运行再故障仿真结果

为了验证非全相运行时再发生线路故障时本方法的有效性，在0.3 s分别设置线路26-29、26-25两侧B相断路器跳开，形成B相断开的线路非全相运行状态，再在0.35 s时设置发生AG、AC相间短路（AC）、AC相间接地短路（ACG）、C相接地（CG）故障进行试验，过渡电阻为300Ω。

0.35 s时线路26-29在距离母线26的5%处发生经300Ω过渡电阻接地故障，仿真结果如附录A图A5所示。由图A5可见，发生非全相运行时非全相运行线路两侧母线的节点注入故障电流幅值与正常母线相等，接近于零，K不满足故障判断阈值，算法可靠不会导致误动。0.35 s发生故障后，Id26、Id29迅速增大为最大值和次大值，稳态值分别为0.215 5、0.012 6 kA，正常节点28的故障注入电流幅值Id28最小，稳态值为0.002 9 kA，K为74.310，远大于设定阈值，能够准确识别出故障线路26-29。

4.2.3系统振荡及再故障时的仿真结果

为了检验本算法在系统振荡及再故障时的有效性，设线路17-27在0.2 s时发生三相短路故障，在0.3 s时跳开线路17-27两侧断路器切除故障，造成系统的暂态稳定破坏来模拟系统振荡［17］。

当系统发生振荡后，线路26-29于50%处在0.35 s发生ABG故障，仿 真数 据如 附录B表B1所示，各节点故障注入电流幅值如附录A图A6（a）所示，K的变化曲线如图A6（b）所示。由图可见，0.3 s系统开始振荡后各节点的故障注入电流幅值均为0，本方法不会发生误动。线路26-29在0.35 s发生ABG故障、过渡电阻为0.01Ω，节点26、29的故障注入电流幅值Id26、Id29迅速增大，而正常节点28的故障注入电流幅值Id28保持在0附近。由保护故障判据检测出线路26-29故障，表明在系统振荡中再发生线路故障且线路拓扑结构未受到破坏时，本方法能够正确检测故障线路，不受系统振荡的影响。

4.2.4线路参数存在误差时的仿真结果

为了验证本算法在电气参数变化时的性能，设置线路26-29、26-28的线路参数误差分别为1%、5%，过渡电阻分别为0.01Ω、300Ω，不同位置发生AG故障的仿真结果如附录B表B2和表B3所示。

由表B2和表B3可见，当故障线路26-29、相邻正常线路26-28分别存在参数误差时，仅对误差线路两侧的节点故障注入电流幅值造成小的影响，对其他母线的节点故障注入电流幅值没有影响，不影响三者的大小排序关系，比值K均大于阈值，能够准确地检测出故障线路26-29。

5 算法动作时限分析

本算法采用区域集中式的广域后备保护系统，由区域内各子站PMU采集电气量，计算得到各自的基波相量，上送至区域决策中心，再由区域决策中心根据广域后备保护算法，进行故障线路的检测。

在广域保护启动后，各子站将定时上传各采样时刻前1/4个周期内所有采样点的电压、电流基波相量。上传时间间隔为1/4个周期（非实时上传数据），减轻了广域通信网络的负担。

设区域Z1中线路26-29距母线26的5%、95%处0.3 s发生A相接地故障，过渡电阻为300Ω，K的变化曲线如附录B图B1所示。由图B1可见，两种故障情景下K在故障发生0.3 s后约1个周期趋于稳定，此时进入故障检测阶段。

根据连续3个K满足K＞Kset的保护判据，本算法在故障发生1个周期后第3次数据上送时检测出故障，故障检测时间最大为5/4个周期。再考虑到通信传输延时（广域网络延时一般为50 ms［17］），故障检测时间极限为70 ms，可满足广域后备保护需要，比传统后备保护动作时间有较大提前。

实际上，对于一个电网有多种PMU布局策略，本文算法中节点故障注入电流相量（式（19））在其他布局策略也适用。对于一个区域，只要估计出其中各节点的注入电流和节点电压，通过本文判据就能检测出故障线路。某线路一端有PMU，另一端没有布置PMU，该端的注入电流和节点电压可通过与其相邻线路的各母线PMU估计，如果与其相邻某线路的对侧母线没有布置PMU，则通过后者母线的相邻PMU类似估计得到，同样可检测出故障线路。

6 结语

本文利用区域中各PMU电压、电流及节点故障注入电流构成广域后备保护算法，有以下结论。

1）算法简单。通过对未布置有PMU节点的电压、注入电流的估计，将节点电压方程运用到间隔母线布置PMU的子区域，减小通信量和计算量。

2）由于采用故障分量，在各种故障情况下均能检测出故障线路，所提算法在原理上不受故障位置、故障类型、过渡电阻的影响。采用最大值与第三大值的比值作为判断量，能够适应各种故障情景。

3）在系统振荡再故障、非全相运行再故障等情景下，仍能检测出故障线路，并且具备一定的抗参数变化能力。

所提算法与区域拓扑结构相关，未考虑相邻线路复故障及测量误差的影响，后续将研究有限PMU配置情况下广域后备保护算法的抗异常数据能力。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。