导管螺旋桨结构参数对永磁电机推进器效率的影响*

汪宗彪, 田海涛, 姜淑忠, 罗 响

(1. 上海交通大学 电子信息与电气工程学院 电气工程系, 上海 200240；2. 中国舰船研究设计中心， 湖北 武汉 430064)

0 引 言

自主/遥控水下机器人(ARV)是深海探测和开发中的重要设备。电机推进器作为ARV的动力核心部件，其设计直接关系到ARV的动力性能、续航能力等技术指标。直驱式电机推进器主要由推进电机、导管和螺旋桨构成。推进电机大多采用永磁电机，其结构简单、调速范围宽、功率密度高、效率高[1]。与普通无导管螺旋桨相比，导管螺旋桨使水流定向通过螺旋桨，在载荷较重时推进效率高、推力大[2]。

由于ARV所携带的电池电能有限，在推进器设计时希望尽可能提高推进器的整体效率，在保证ARV动力性能的同时，降低能耗，提高续航能力。永磁推进电机负载运行时的效率可以达到90%以上，并且在较宽的转速范围内均能保持较高的效率，通过优化电机设计来提高推进器整体效率的空间不大。因而可以通过优化导管螺旋桨的结构设计，为已有的推进电机匹配最佳的导管螺旋桨，提高推进器的整体效率。

导管螺旋桨结构优化涉及水动力性能计算，主要有2类方法：螺旋桨环流理论方法和计算流体力学(CFD)方法。螺旋浆环流理论方法是将流体力学中的机翼理论应用于螺旋浆作用力的研究，包括升力线理论、升力面理论和面元法[3]。文献[4]采用桨升力面法与导管面元法耦合的方法来预估导管可调螺距螺旋桨水动力性能，通过迭代计算考虑桨和导管的相互影响。实践中该方法要求经验性强，并且不能给出复杂流场的细节信息。与螺旋桨环流理论方法相比，CFD方法的流动控制方程考虑了流体黏性作用，能真实地反映流体流动状态，较准确地计算水动力性能，因此广泛应用于螺旋桨水动力分析中[5-7]。

目前关于导管螺旋桨结构参数优化的研究较多[8-11]，但在优化设计时只考虑了导管螺旋桨自身的推进效率，优化得到的导管螺旋桨结构参数无法保证推进器整体效率最大化。本文将导管螺旋桨与推进电机结合，搭建导管螺旋桨CFD仿真模型及推进电机本体与控制系统的联合仿真模型，分析在导管螺旋桨产生的总推力一定时，其结构参数与推进器整体效率之间的关系，为导管螺旋桨的优化设计提供依据，以提高推进器整体效率。

1 导管螺旋桨三维建模

1.1 导管螺旋桨结构参数

螺旋桨的主要结构参数包括桨叶切面类型、叶数、直径、盘面比、螺距、毂径比和纵倾角等。螺旋桨正车旋转时迎水的一边称为导边，另一边称为随边。导管的主要结构参数包括剖面类型、长径比和攻角等[12]。

1.2 螺旋桨三维坐标计算

螺旋桨三维建模即将不同半径处叶切面投影的二维型值点还原到对应的三维空间坐标系中。螺旋桨叶切面投影原理如图1所示，其中OH为基线，θ为纵倾角，φ为螺距角。坐标系Oxyz为全局坐标系，xOy平面与螺旋桨轮毂端面平行。坐标系O1x1y1z1与Oxyz平行。O2点为叶切面与螺旋线的切点，O2z2轴经过叶切面的最厚处。M为叶切面轮廓上任意一点，A点为O1在圆柱底面的投影点，B点为M在圆柱底面的投影点。图1右侧为圆柱面展开而成的平面，其中M1、A1、B1分别与左侧图中的M、A、B点相对应[13]。

图1 螺旋桨投影原理

根据螺旋桨投影原理推导出坐标转换式[14]：

(1)

式中：Ri为各叶切面对应的半径值；W为切面最厚处至导边的长度；(X,Y)为Ri处叶切面投影的型值点二维坐标；(x,y,z)为还原到三维空间的型值点坐标。

1.3 螺旋桨模型

以上海交通大学水下工程研究所万米ARV的主推进器为研究对象，其参数如表1所示。针对主推进器所使用的螺旋桨，基于式(1)使用MATLAB软件编程，计算各叶切面型值点的三维笛卡尔坐标，将计算得到的各型值点坐标导入SolidWorks软件，经过曲线拟合、曲面填充、放样、圆周阵列等操作完成不同结构参数螺旋桨的实体建模，如图2所示。

表1 万米ARV主推进器参数

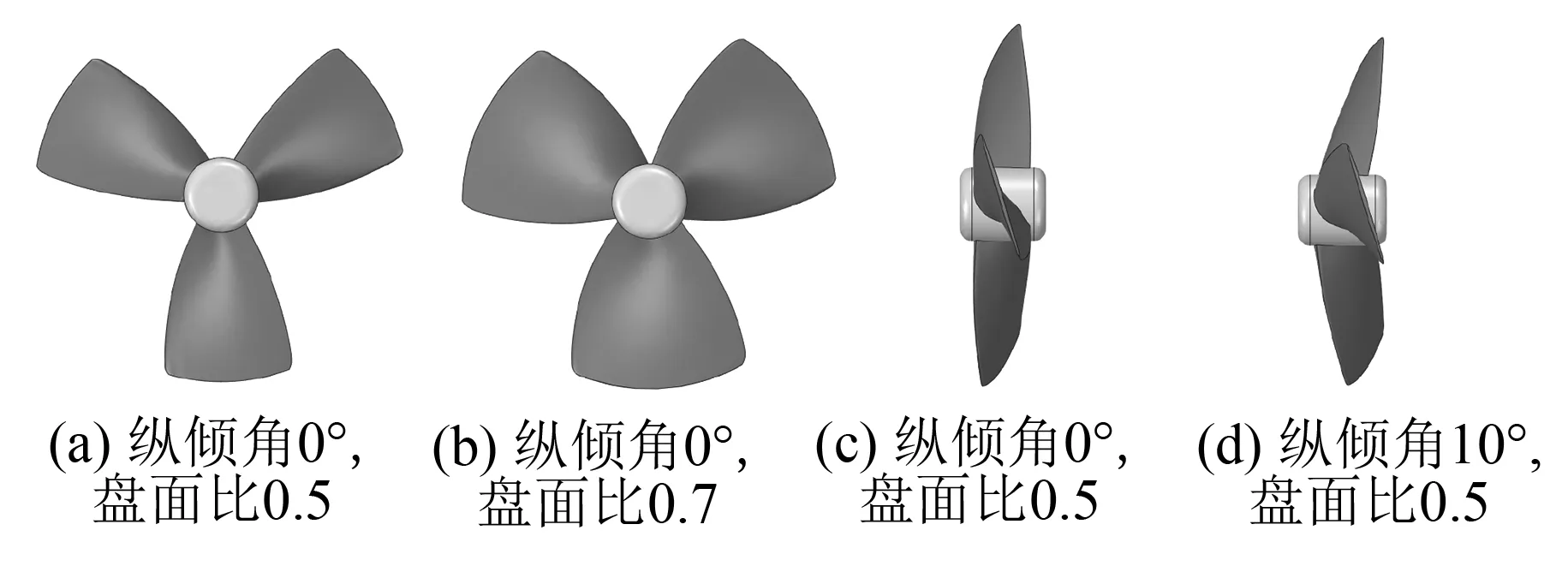
图2 不同盘面比和纵倾角的螺旋桨模型

2 导管螺旋桨水动力性能计算

2.1 螺旋桨水动力性能

螺旋桨水动力性能是指螺旋桨在水中运动时所产生的推力、消耗的转矩和效率与其运动(进速VA和转速n)之间的关系，可用下列无量纲系数表示[12]：

(2)

(3)

(4)

(5)

(6)

(7)

式中：J为进速系数；KTP、KTN和KT分别为螺旋桨推力系数、导管推力系数和总推力系数；Tprop、Tduct和T分别为螺旋桨推力、导管推力和总推力；KQ为扭矩系数；ρ为水的密度；η为导管螺旋桨效率。

2.2 CFD仿真模型

使用Fluent有限元仿真软件计算导管螺旋桨的水动力性能，采用多重参考系(MRF)方法模拟螺旋桨的旋转运动。

计算域设置如图3(a)所示，整个流场区域分为2部分：包含螺旋桨的内部动域和包含导管的外部静止域。外部静止域直径为6D(D为螺旋桨直径)，速度入口距螺旋桨中心4D，压力出口距螺旋桨中心5D。采用非结构化网格剖分，边界层设置为5层，网格数约1.5×106，导管螺旋桨表面网格如图3(b)所示。采用standardk-ε湍流模型和coupled压力速度耦合求解方法进行求解。

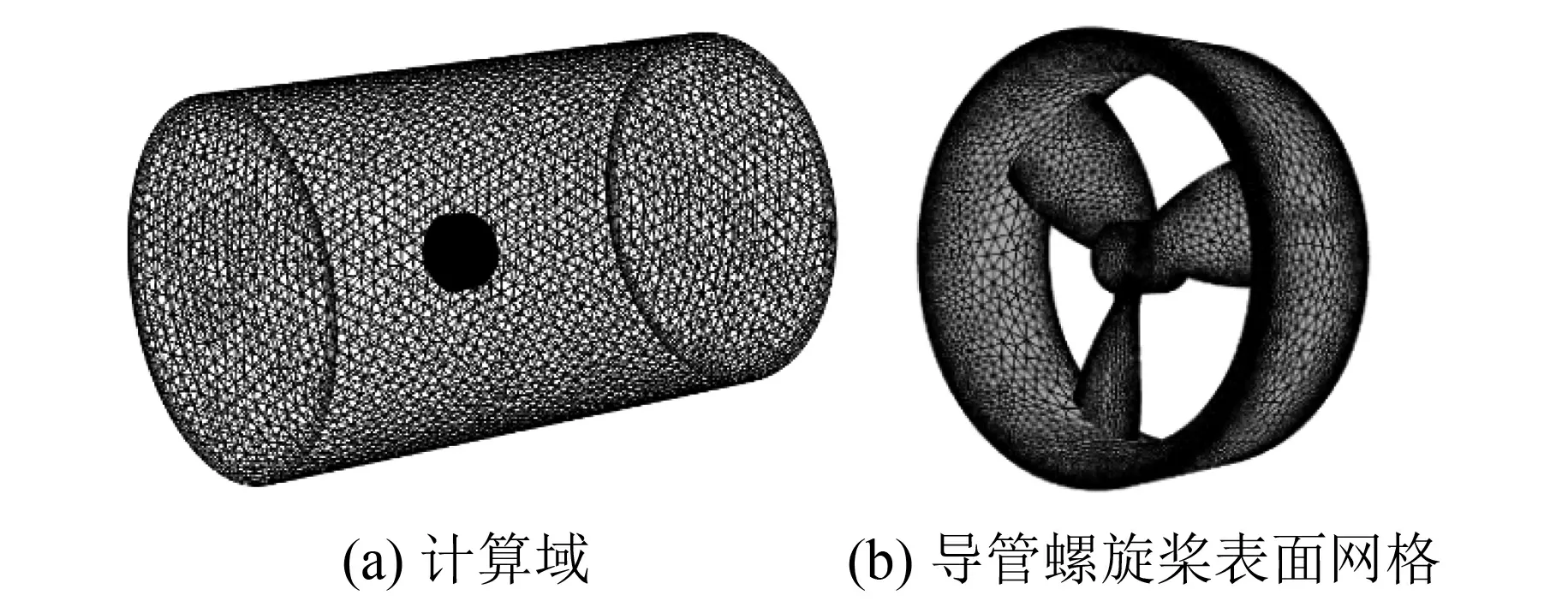
图3 计算域及导管螺旋桨网格

2.3 计算结果

在敞水情况下，对No.19A+Ka4-70导管螺旋桨在进速系数0.1～0.7范围内进行水动力性能计算，并与上海交通大学船舶流体力学研究所公开的试验数据对比[12]，如图4所示。可以看出，计算结果与试验数据吻合度较好。在各进速条件下，推力系数、扭矩系数及效率的最大误差不超过7%，验证了CFD仿真模型的可靠性。

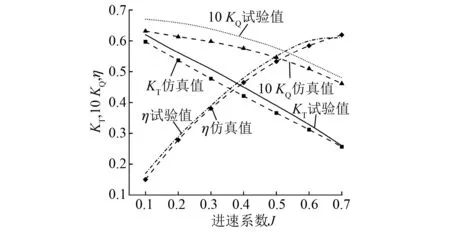
图4 No.19A+Ka4-70导管螺旋桨水动力性能曲线

在静水情况下，对本文研究的SUB380导管螺旋桨在转速200～980 r/min范围内进行水动力性能计算。在水池中对主推进器进行推力试验，将其安装在推力测量装置上，放入水池中，如图5、图6(a)所示。拉压力传感器测得的推力值经过换算得到主推进器实际产生的推力，根据图6(b)可计算出力臂换算系数为1.083。搭建的试验平台如图7所示，推进电机基于id=0的磁场定向控制(FOC)算法，采用PI调节器实现转速、电流双闭环控制。将仿真结果与试验结果对比，如图8所示，可以看出，两者吻合度较好，最大误差不超过8%，验证了CFD仿真的准确性。

图5 主推进器

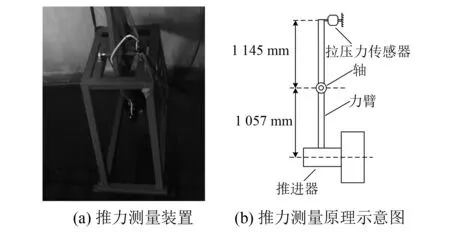
图6 推力测量装置及推力计算示意图

图7 推力试验平台

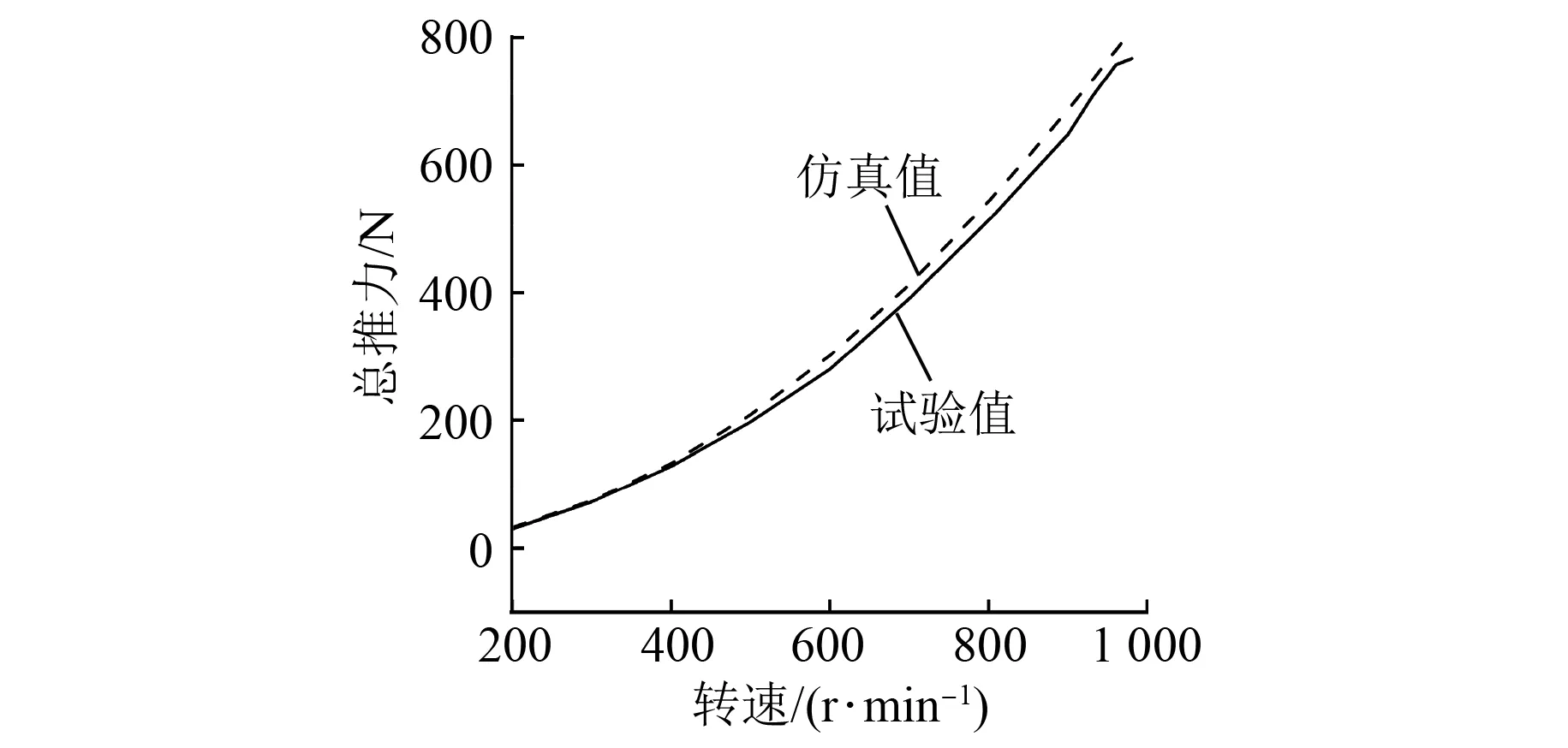
图8 SUB380导管螺旋桨总推力仿真值与试验值对比

3 推进电机联合仿真

3.1 电磁仿真模型

推进电机结构参数如表2所示。在Maxwell软件中搭建推进电机二维电磁仿真模型，如图9所示。计算负载时的铜耗和铁耗，从而计算电机效率。

表2 推进电机结构参数

图9 推进电机二维电磁仿真模型

3.2 联合仿真模型

Maxwell只能提供正弦形式的电源激励，而实际电机控制系统中采用变频器供电，电流中存在大量谐波，使得绕组和铁心中产生的损耗增加[15]。为了充分考虑谐波电流的影响，使仿真结果更贴合实际，搭建了基于Maxwell、Simplorer和MATLAB的联合仿真平台。其中，在MATLAB中搭建矢量控制系统，在Simplorer中搭建功率电路和信号采集模块，作为桥梁实现电机本体与控制系统的数据传递和交换，如图10、图11所示。

图10 MATLAB中搭建的矢量控制系统

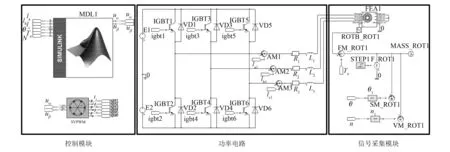
图11 Simplorer中搭建的功率电路和信号采集模块

4 导管螺旋桨结构参数变化

在SUB380导管螺旋桨直径D为300 mm、进速VA为2.45 m/s、产生的总推力T为300 N的条件下，研究盘面比、纵倾角和导管攻角变化时所需的电机转速、转矩，计算导管螺旋桨效率、电机效率和推进器整体效率，分析导管螺旋桨结构参数变化对推进器整体效率的影响。

4.1 盘面比变化

保持螺旋桨纵倾角为0°、导管攻角为0°，盘面比在0.45～0.70范围内变化。仿真得到电机转速、转矩与盘面比之间的关系如图12所示，导管螺旋桨效率、推进器整体效率与盘面比之间的关系如图13所示。

图12 盘面比变化时的转速和转矩

图13 盘面比变化时的推进效率

由图12、图13可以看出，螺旋桨盘面比变化引起的转速、转矩和推进效率变化较小。随着盘面比增大，推进器整体效率呈略微降低的趋势，因此在螺旋桨设计时可选取较小的盘面比，以减少材料使用，一方面可节约成本，另一方面也能减轻螺旋桨重量。但盘面比过小会带来螺旋桨强度问题，需要进行强度校核。

4.2 纵倾角变化

纵倾螺旋桨一般均是向后倾斜，以增大桨叶与船体间的间隙，减小螺旋桨诱导的船体振动，但考虑到桨叶强度问题，纵倾角不宜过大，一般小于15°。

保持螺旋桨盘面比为0.5、导管攻角为0°，纵倾角在0°～15°范围内变化。仿真得到电机转速、转矩与盘面比之间的关系如图14所示，导管螺旋桨效率、推进器整体效率与盘面比之间的关系如图15所示。

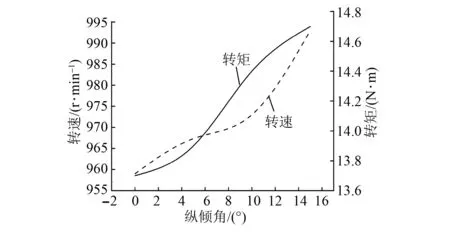
图14 纵倾角变化时的转速和转矩

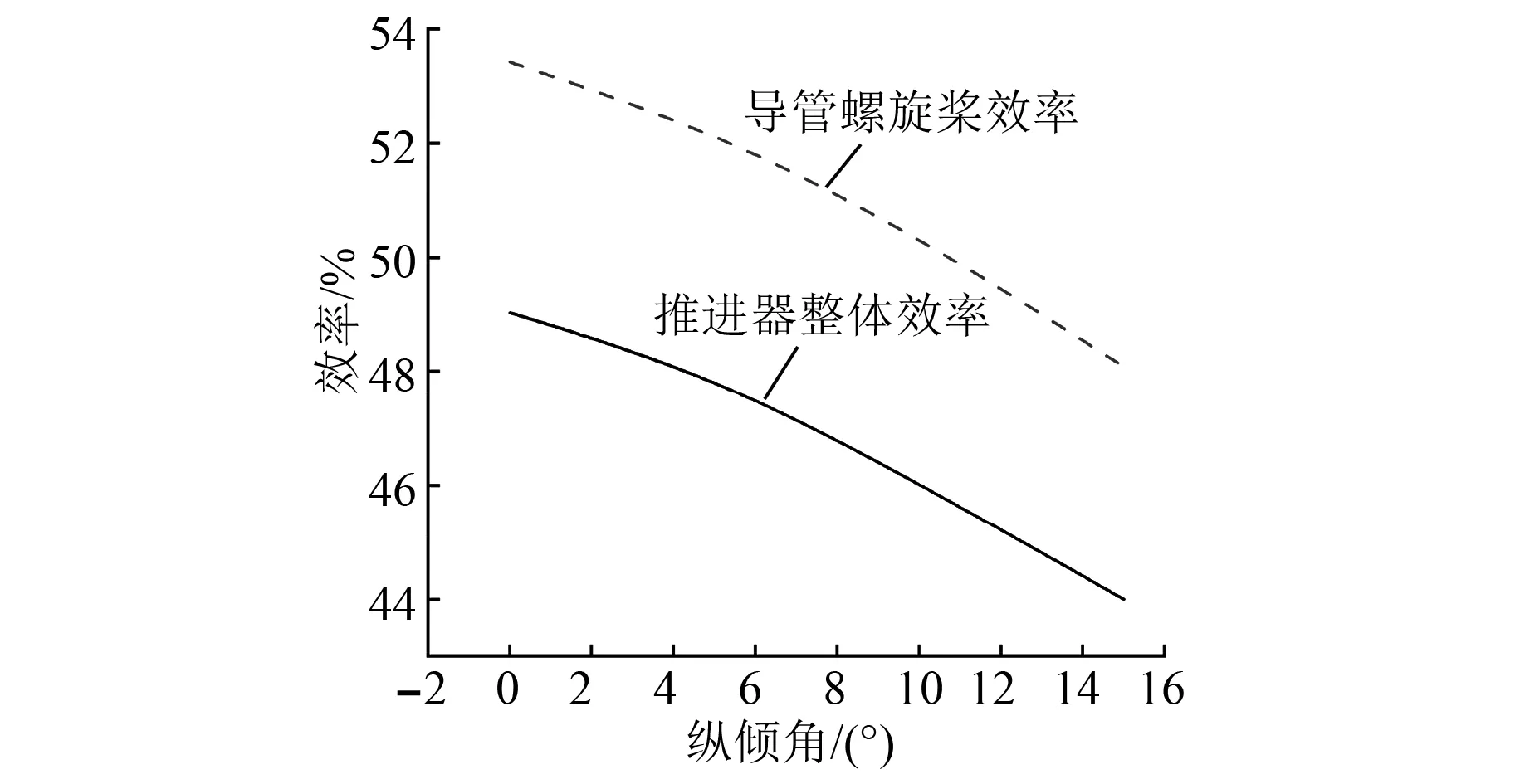
图15 纵倾角变化时的推进效率

由图14和图15可以看出，随着纵倾角增大，推进电机转速和转矩增大，输出功率增加，而推进器整体效率降低，即推进器消耗的功率增加。因此在设计螺旋桨时应尽量选取小的纵倾角。

4.3 导管攻角变化

保持螺旋桨盘面比为0.5、纵倾角为0°，导管攻角在-8°～8°范围内变化。攻角为-8°、0°和8°的导管剖面如图16所示。仿真得到电机转速、转矩与导管攻角之间的关系如图17所示，导管螺旋桨效率、推进器整体效率与导管攻角之间的关系如图18所示。

图16 不同攻角的导管截面

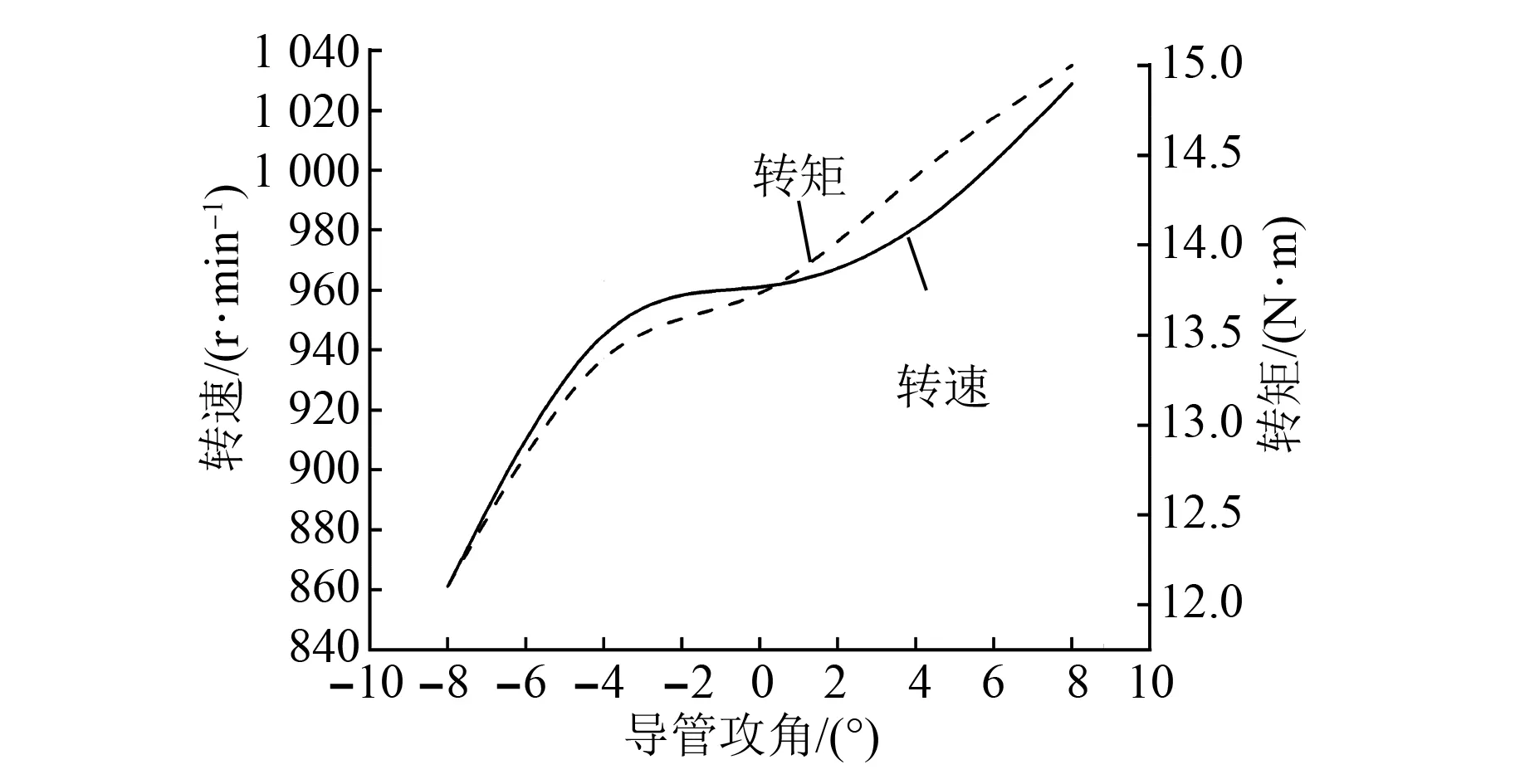
图17 导管攻角变化时的转速和转矩

图18 导管攻角变化时的推进效率

由图17和图18可以看出，导管攻角变化引起的转速、转矩和推进效率变化较大。随着导管攻角从负到正变化，推进电机转速和转矩增大，输出功率增加，而推进器整体效率降低，即推进器消耗的功率增加。因此，在设计导管时可选取负攻角，但负攻角会使导管入口增大而出口减小，阻碍流体流出，需对流场情况作进一步分析。

5 结 语

针对传统螺旋桨优化设计未考虑推进器整体效率的问题，本文以万米ARV主推进器为研究对象，将导管螺旋桨与推进电机结合，搭建导管螺旋桨CFD仿真模型及永磁推进电机本体与控制系统联合仿真模型，分析了在导管螺旋桨产生的总推力一定的条件下，其结构参数与推进器整体效率之间的关系，为导管螺旋桨的设计和优化提供了参考。结论如下：

(1) 盘面比变化对推进器整体效率的影响较小，在设计时可适当选取小的盘面比，以节省材料，但应考虑强度问题。

(2) 纵倾角越大，推进器整体效率越低，在设计时应选取小的纵倾角。

(3) 导管攻角变化对推进器整体效率的影响较大，攻角由负到正变化时效率降低，在设计时可选取负导管攻角，但需对流场情况作进一步分析。