永磁辅助同步磁阻电机改进型滑模观测器无位置传感器控制

吴昌隆, 储剑波

(南京航空航天大学 自动化学院，江苏 南京 211100)

0 引 言

永磁辅助同步磁阻电机(PMASynRM)具有高调速范围、高性价比、高容错能力等优势，在电动汽车、航空航天、伺服控制等领域均有广泛应用[1-4]。与传统永磁同步电机(PMSM)相比，PMASynRM的电磁转矩以磁阻转矩为主，永磁转矩为辅，其成本相对更低，发展前景较为广阔[5]。传统方法下电机转子角度转速信息通过机械传感器获取，例如旋转变压器和光电编码器等[6]，但增加了成本且易受环境因素的影响。因此，PMASynRM的无位置传感器矢量控制受到了广泛关注。

针对电机转子角度和速度的估算，无位置传感器矢量控制方法主要包括适用于低速场合的低频信号注入法、高频信号注入法，适用于中高速的开环估算法、模型参考自适应法、滑模观测器(SMO)法、状态观测器法和扩展卡尔曼滤波器法等。由于PMASynRM具有磁路饱和(包括交叉饱和)现象，高鲁棒性、抗干扰性的滑模控制算法得到更广泛的关注与应用。文献[7-8]用sat饱和函数代替理想滑模动态中的sgn符号函数，控制边界层的取值范围，有效减小了抖振。文献[9]用双曲正切函数代替符号函数，优点是抑制抖振效果好，缺点是影响了系统的控制精度。文献[10]用Sigmoid函数代替符号函数，进一步削弱系统的高频抖振信号。文献[11]将变指数趋近律引入滑模结构，其速度跟踪、抗扰动抖振等特性良好。

超螺旋滑模观测器(ST-SMO)算法是高阶滑模算法，区别于传统的一阶SMO算法，二阶的ST-SMO可以有效地抑制系统抖振。ST-SMO滑模面内的轨迹不是近似的直线，而是绕原点螺旋分布，且ST-SMO算法对系统非连续项积分，提高了系统的连续性与鲁棒性。算法能够有效抑制高频抖振，提升动稳态性能，且算法较容易实现[12-14]。

为实现PMASynRM的无位置传感器矢量控制，提出一种改进型SMO传感器矢量控制算法。本文基于ST-SMO搭建滑模变结构，使用Sigmoid函数代替ST-SMO中sgn符号函数，并采用锁相环(PLL)估算转子角度，提取速度信息。

1 PMASynRM的滑模观测器

1.1 电机数学模型

PMASynRM是一种结合PMSM与同步磁阻电机优点的电机，其具有调速范围宽、功率密度高、性价比高等显著优点。与传统PMSM所采用的钕铁硼永磁材料相比，PMASynRM通常采用铁氧体磁极材料，成本更低。

为了方便分析电机的特性，对理想状态下的数学模型进行假设：忽略铁心饱和及磁滞损耗；忽略永磁体的阻尼作用；只考虑基波，不考虑高次谐波；三相绕组互相对称。

得到两相静止坐标系中电机数学模型的表达式如下：

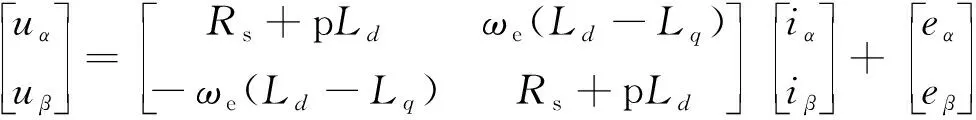
(1)

1.2 传统滑模观测器模型

传统的SMO基于静止坐标系下的数学模型，提取扩展反电动势参数为位置信息，对扩展反电动势进行反正切函数计算，从而获取电机角度速度信息。传统SMO算法实现原理框图如图1所示。

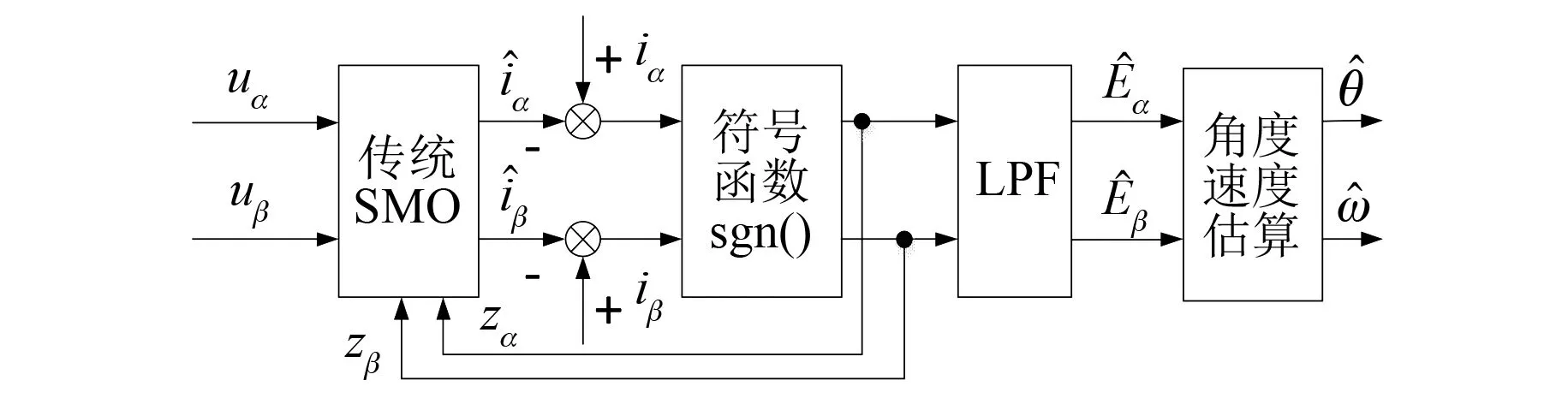
图1 传统SMO算法原理框图

对式(1)进行整合变换，电机的电流方程如下：

(2)

传统的SMO取定子电流作为滑模面s(x)=0的目的轨迹，滑模切换面方程如下：

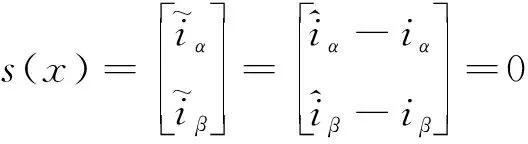
(3)

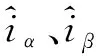
根据SMO变结构矢量控制的原理，可得定子电流误差方程：

(4)

(5)

对式(4)和式(2)作差，得定子电流误差：

(6)

当系统状态变量到达滑模面时，即满足式(3)，对式(6)等效化简可得：

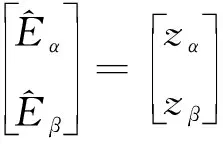
(7)

经过低通滤波器(LPF)的处理，扩展反电动势估计值的幅值和相位均有一定改变，尤其是相位延迟，弥补方法为在原转子位置计算结果基础上加入角度补偿。

(8)

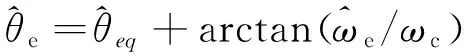
(9)

2 改进型SMO设计

针对传统滑模观测器无位置传感器控制的高频抖振、相位延迟、抗干扰性差等特点，设计改进型SMO算法，优化控制性能。

2.1 边界区设计

常用的SMO无位置传感器矢量控制算法采用sgn符号函数作为边界区。为了减小滑模系统的高频抖振现象，设计Sigmoid函数作为边界区:

(10)

式中:a为收敛因子，正常数，其大小影响着函数的收敛性。

Sigmoid函数示意图如图2所示。

图2 Sigmoid函数示意图

2.2 ST滑模算法设计

以ST算法的理论为基础，并结合Sigmoid理想滑模边界函数，本文设计了ST-SMO无位置传感器控制方法。ST算法数学模型表达式如下[将Sigmoid(x)简写为sig(x)]:

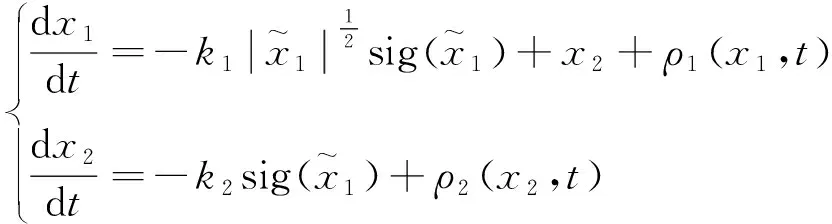
(11)

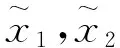
ST-SMO可以在有限时间内收敛至滑模面，但满足以下2个条件:

(1) 系统的扰动项满足边界条件:

(2) 滑模增益系数满足最小组要求：

(13)

为了简化算法，δ2取值为0，则取值ρ2=0，式(12)、式(13)简化为

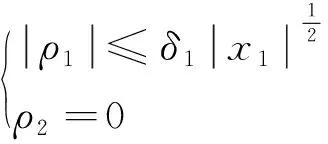
(14)

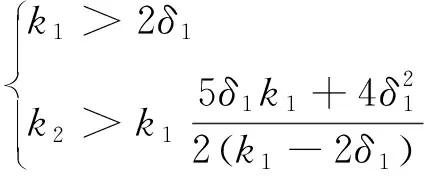
(15)

式中:δ1为正常数。

根据ST-SMO原理设计的PMASynRM定子估算电流方程如下：

扰动项定义为

(17)

将式(16)与式(2)作差，得到定子电流误差式：

(18)

根据SMO的等效控制原理，当观测器的状态变量到达滑模面时，即定子电流误差为0时，控制量可看作等效控制量。将式(6)滑模切换面方程代入式(18)，得控制量方程：

(19)

通过ST-SMO算法提取了PMASynRM的扩展反电动势，其具有精度较高、抑制抖振性能强、抗干扰性好的优点。

2.3 PLL设计

为确保提取转子位置信息的精度，采取PLL的方式进行转子位置与速度跟踪，其原理如图3所示。

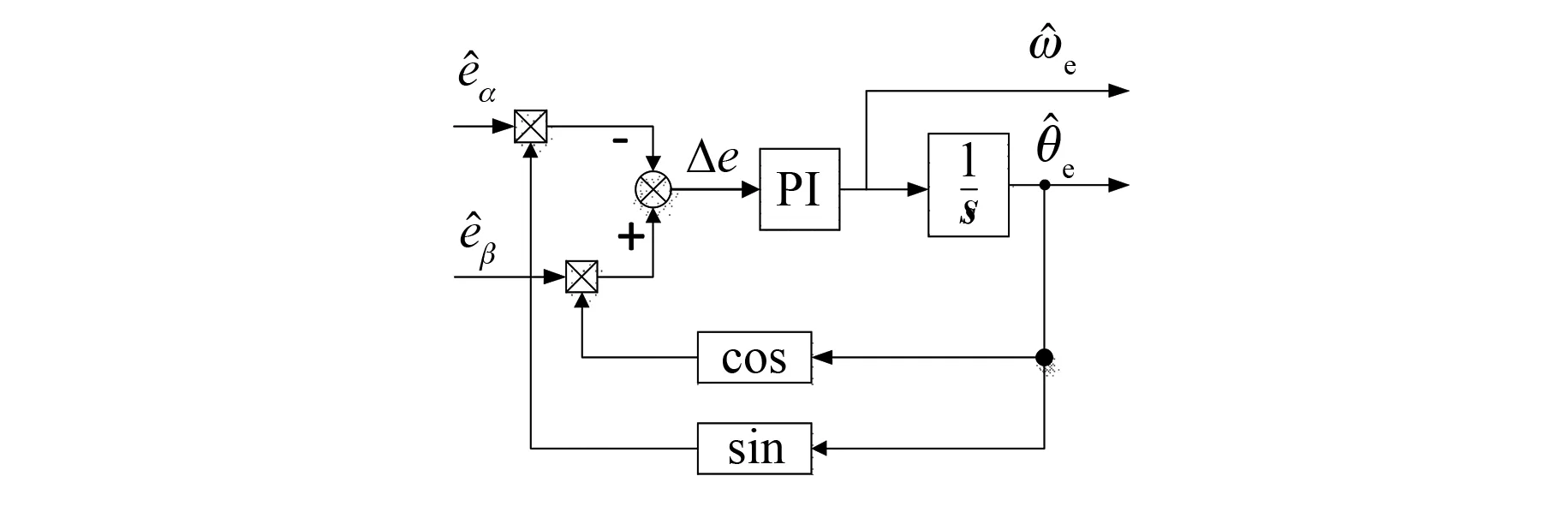
图3 转子位置与速度跟踪法

锁相环PI控制器的输入信号表达式为

(20)

当转子位置观测误差小于30°，可化简式(20)为

(21)

该误差经过PI调解后即可得转子角速度的估计值。

3 仿真验证与结果分析

3.1 系统仿真模型

基于ST-SMO算法、PLL等搭建的PMASynRM无位置传感器矢量控制系统如图4所示。电机矢量控制系统包括电压电流PI控制器、最大转矩电流比(MTPA)模块、空间矢量脉宽调制(SVPWM)模块、SMO无位置传感器模块等若干子系统模块。

图4 PMASynRM无位置传感器矢量控制系统框图

在MATLAB/Simulink工具中搭建电机无位置传感器矢量控制系统模型，如图5所示，其中主要包括电机数学模型与无位置传感器双闭环矢量控制模型。无位置传感器双闭环矢量控制模型中，其关键算法模块如图6所示，主要包括ST-SMO算法与PLL算法模块。

图5 电机无位置传感器矢量控制系统模型

图6 ST-SMO及PLL算法模块

3.2 仿真结果及分析

在MATLAB/Simulink搭建PMASynRM无位置传感器矢量控制系统并仿真，电机仿真参数如表1所示。

表1 PMASynRM参数表

采用PMASynRM矢量控制，仿真条件为,电机给定转速n*=8 000 r/min，给定形式为斜坡函数，斜率为2 000 r/(min·s)；直流侧电压Udc=310 V；负载转矩初始给定TL=0.1 N·m；仿真时长为10 s，在t=1 s时系统切换成无位置传感器算法，将SMO估算的电机转速和角度信息反馈至转速环和电流环。经过整定，确定ST-SMO的滑模增益系数k1=3.5，k2=0.000 1，根据试凑法确定Sigmoid函数中的收敛因子a=2。

图7是8 000 r/min转速下传统SMO和改进型SMO无位置传感器算法的电机转速波形对比。

图7 加速度2 000 r/(min·s)的电机转速波形

由图7(a)和图7(b)的波形对比可知，采用常规SMO无位置传感器矢量控制方案的电机转速振荡较大，动稳态性能一般；采用改进型ST-SMO无位置传感器控制方案电机稳态时的转速振荡减小，电机的实际转速与给定转速误差很小，转速误差在0.5%以内。证明改进型SMO无位置传感器算法的动稳态性能较好。

图8和图9是在8 000 r/min转速下传统SMO与改进型SMO无位置传感器算法的扩展反电动势波形对比。

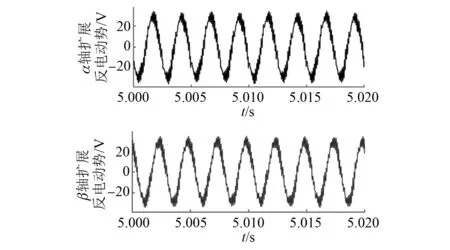
图8 传统SMO静止坐标轴扩展反电动势波形

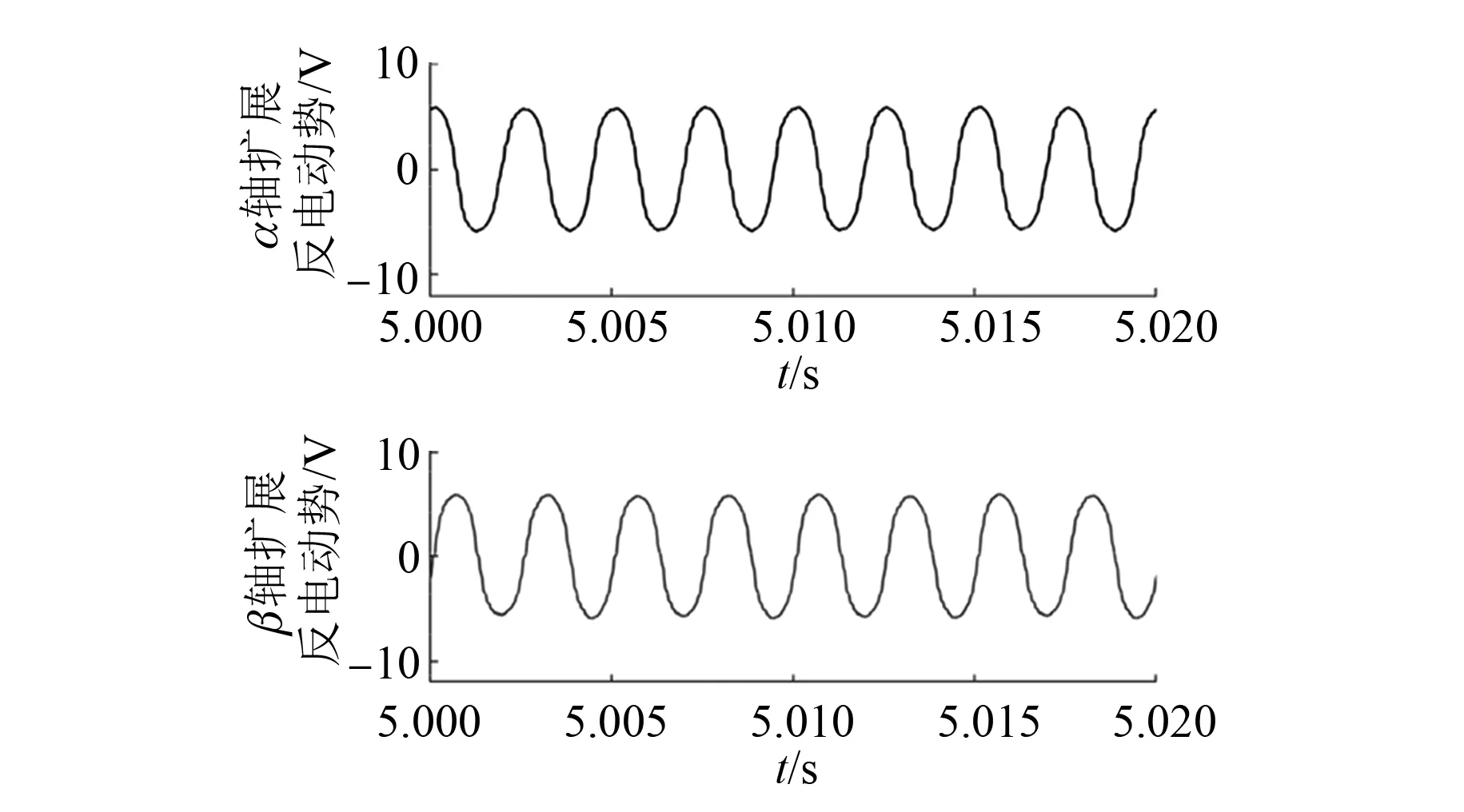
图9 改进SMO静止坐标轴扩展反电动势波形

对比图8和图9波形，采用改进型SMO算法所提取的扩展反电动势波形幅值小于传统SMO算法，但是其误差比例也明显小于传统SMO算法。使用传统的SMO无位置传感器算法，所得位置信息扩展反电动势具有强烈的高频抖振现象，需经过LPF削弱高频抖振信号。而ST-SMO算法所得扩展反电动势波形为较理想的正弦波形，无高频抖振现象。证明改进型SMO能够抑制高频抖振，精确地提取电机位置信息。

图10和图11是在8 000 r/min转速下传统SMO与改进型SMO无位置传感器算法的电磁转矩波形对比。

图10 传统SMO电磁转矩波形

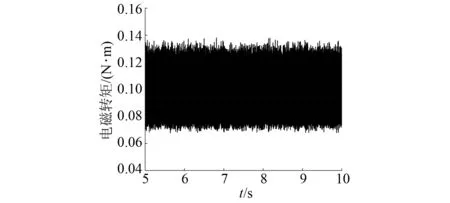
图11 改进SMO电磁转矩波形

由图10和图11波形的对比可知，改进型SMO算法电磁转矩的振荡小于传统SMO算法，证明ST-SMO算法下的电机转矩输出的动稳态性能提升。

提升给定转速斜率至4 000 r/(min·s)，t=0.5 s时刻切换无位置传感器算法，其余参数不变。转速波形对比如图12所示。

图12 加速度4 000 r/(min·s)的电机转速波形

由图12可知，在增大转速斜率的情况下，改进型SMO更快到达稳态转速，转速振荡较小，因而改进型SMO动稳态性能更好。

对电机系统做突加负载仿真测试。给定转速斜率设为2 000 r/(min·s)，t=2 s时切换无位置传感器双闭环，t=6 s时突加负载0.5 N·m。突加负载时的转速和电磁转矩波形对比如图13和图14所示。

图13 突加负载0.5 N·m时电机转速波形

图14 突加负载0.5 N·m时电磁转矩波形

由图13波形的对比可知，在突加负载前，传统SMO转速超调量1.34%，改进型SMO的转速超调量1.125%，明显小于传统SMO；突加0.5 N·m负载后，2种方法的转速突降且超调量接近，但改进型SMO的转速恢复较快，且转速稳态振荡较小。由图14的波形对比可得，传统SMO与改进型SMO的电磁转矩在突加负载后峰值分别为1.85 N·m和0.9 N·m，且改进型SMO的转矩稳态波动明显小于传统SMO。上述波形说明ST-SMO算法的抗抖振性能好，动稳态性能更优。

通过转速突增突减的系统仿真验证ST-SMO算法的鲁棒性。在t=6 s对系统给定转速突增阶跃300 r/min，其余仿真条件同上，仿真波形如图15所示。在t=6 s对系统给定转速突减阶跃300 r/min，其余仿真条件同上，仿真波形如图16所示。

图15 给定转速突增时仿真波形

图16 给定转速突减时仿真波形

由图15和图16可知，电机突加转速阶跃300 r/min时，转速恢复时间0.5 s，转速超调量0.88%，转矩最大值0.7 N·m；电机突减转速300 r/min时，转速恢复时间0.8 s，转速超调量1.61%，转矩最小值-0.03 N·m。ST-SMO算法在转速突增突减情况下均能较快恢复稳态，且静态误差很小。说明ST-SMO无位置传感器算法的动稳态特性好，鲁棒性强。

4 结 语

为提高PMASynRM无位置传感器控制的动稳态性能，减少高频抖振，基于扩展反电动势设计了一种改进型SMO无位置传感器算法。算法采用ST-SMO获取位置信息，使用Sigmoid函数代替sgn函数，并通过PLL提取位置转速信息。将改进型SMO无位置传感器算法与传统SMO对比分析，仿真结果表明，改进型SMO无位置传感器矢量控制系统能较好地抑制高频抖振，抗干扰性较好，且动稳态性能更优良。