基于提升数学核心素养的课堂教学模式的案例分析
2021-08-06陈志强
陈志强

摘要:在高中课程改革不断深化的背景下,本文以《直线与平面垂直》的教学设计为切入口,探讨在基于提升高中生数学核心素养的课堂教学模式研究中的一些做法。
关键词:数学核心素养;教学模式;案例分析
中图分类号:G633.6 文献标识码:A文章编号:1992-7711(2021)11-111
教学模式是构成课程和作业、选择教材、提示教师活动的一种范式。因此教学模式可以定义为是在一定教学思想或教学理论指导下建立起来的较为稳定的教学活动结构程序。本文结合《直线与平面垂直》教学设计为例,谈一谈笔者探究的基于提升高中生数学核心素养的课堂教学模式——以问题导学为核心的四环节教学模式。
一、创设情境,引入问题
在课堂伊始,创设合适情境,让学生参与进来,勾起学生的好奇心,进而在情境中提出问题,启发学生思考。
1.回顾旧知,引入课题
问题1:空间内一条直线和一个平面有哪几种位置关系?你能借助手边的课本和笔演示一下吗?
问题2:同学们观察这两幅图,从数学的角度看,有何异同?(PPT展示旗杆和比萨斜塔)
问题3:类似于旗杆与地面的位置关系,你还可以再举其他的例子吗?它们都有怎样的特点?
2.探索观察,抽象概念
问题4:直线与平面满足怎样的条件,才能称“直线与平面垂直”呢?
问题5:同学们回忆一下,前一节课我们是如何判断线面平行的?它的研究方法可以给我们一点启发吗?
问题6:类比线面平行,我们会产生这样的思考,“线面垂直”是否可转化为“线线垂直”呢?
分组活动(或由老师演示):
(1)把纸平放到桌面上,把一支笔直立放到纸面上;
(2)用一个手电筒将其打开,观察两个画笔主体所在的两条垂直线和两个影子主体所在的垂直线之间的两个相对所在位置上的关系;
(3)通过旋转一个手电筒,观察者看到更多的像是影子画笔所在的点直线和小画笔所在之处的点直线之间的相互关系;
问题7:我们在设计中如何使用直线和平面之间的垂直,这样的直线和平面内的直线是怎么样的位置关系?
(4)把一支笔倾斜地放置,观察一支笔所处的直线和影子所处的直线之间是怎么样的位置关系?
(5)注意寻找在一个平面内和与一个倾斜笔触点垂直的圆形画框上的一个影子;
问题8:如何在一条直线和平面内无数条相等的直线之间竖立,这些点和平面之间的位置有什么关系?
问题9:上述发现说明了什么?你能用自己的语言描述直线与平面垂直的定义吗?
概念生成,板书三种语言(文字,图形,数学符号)定义直线与平面垂直。
3.辨析理解、认识定义
(几何画板展示圆锥的生成动画,以形象的数学模型巩固定义的理解。)
问题10:定义中的“任意一条”可以改为“无数条”吗?
问题11:我们在实验中发现,当一条直线和平面呈垂直状时,这条直线和平面内的任何一条直线之间有什么相互关系?
二、探究发现,意义建构
创设情境后的下一个环节是“探究发现,意义建构”,这是课堂的核心环节。“探究发现”的主要意义在于通过调动和培养激发学生对数学的探究积极性和探究兴趣,养成良好的数理学习行为习惯,启发学生的独立思考,“意义建构”的目的在于让学生掌握数学知识,理解知识的本质。根据目前我校学生的情况和特点,在研究问题设计的过程中要求必须符合以下几个条件:(1)考核问题的清晰性;(2)解决问题的深度和层次性;(3)提高了问题的理论实用性。
问题12:我们在实践和理论的基础上,我们如何判定直线与平面垂直呢?你遇到了什么困难?
假设1:如果一条直线和在平面内有一条直线垂直,是否可以用来判断该线与这个平面是否垂直?
假设2:如果一条直线和平面内有无数条相等长度的直线相互垂直,我们可以用来判断直线与这个平面垂直?
假设3:如果一条直线与平面内的两条同时相交的直线垂直,我们可以用来判断这条线与这个平面垂直?
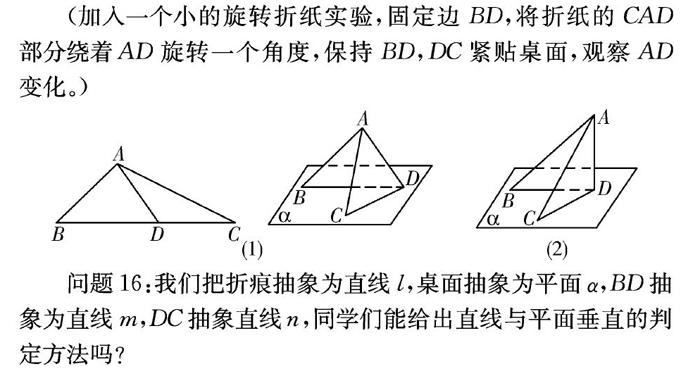
操作一个实验,确认一个猜想:(分组进行三角纸折叠实验)拿出一张三角形纸片,过三角形的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD、DC与桌面接触)。
(将正确的折叠与错误的折叠对比,让学生从线面垂直的定义分析实验结果的合理性。)
问题13:在(1)的折叠中,折痕AD可能与平面垂直吗?为什么?
问题14:如何进行翻折,才能让折痕垂直于其所在的平面?
问题15:由AD与平面内的两条相交直线BD、DC都垂直,进而推导出“直线与平面垂直”,合乎情理吗?
(加入一个小的旋转折纸实验,固定边BD,将折纸的CAD部分绕着AD旋转一个角度,保持BD,DC紧贴桌面,观察AD变化。)
问题16:我们把折痕抽象為直线l,桌面抽象为平面α,BD抽象为直线m,DC抽象直线n,同学们能给出直线与平面垂直的判定方法吗?
问题17:如果直线l与平面α内的两条相交直线m、n都垂直,但不经过它们的交点,那么直线l还与平面α垂直吗?
(引导学生用图形、文字、符号三种语言表示,并明确定理中的5个条件)
问题21:定义和判定定理的共同点是什么?两者相比,判定定理的优越性在哪里?
三、数学应用,巩固新知
根据我校教师多年的实践工作经历和对农村地区学生的理解与认知规律,数学教师在第三个环节中需要设置的主要问题是:(1)根据条件可以得到什么样的结论?(2)根据所求的问题可以溯源到什么?(3)公式或公理在使用时有什么限制条件?
问题18:在正方体ABCDA1B1C1D1中。
(1)判断:直线AC是否与平面CC1D1D垂直?
(2)证明:直线AC⊥平面BB1D1D。
(3)证明:AC⊥BD1。
(让学生对条件和需求进行分析及要求证明的结果,教师在课堂上板书了解题的全过程,引导他们进行归纳。)
四、梳理总结,拓展提升
这一环节不仅在于对所学知识点的归纳分析总结,对于学习的方法与知识点获取路线的分析总结,更是一个对于课堂教学的深化、扩充的过程。总结的方式既可以由老师在学生掌握了任务之后给予教师点拨,也或者可以由老师在实践中进行总结并向学生提出较多的具有扩散性的问题以及如何引起老师与学生一种新的认知冲突,为后续内容的学习提供新的支撑点。
问题19:本节课你学会了哪些判断直线与平面垂直的方法?
问题20:除了新的知识,本节课你还有哪些收获?(掌握了哪些方法?体会了哪些思想?)
课后作业:
必做题:课本38页练习2,3,5,6
拓展题:1.阅读课本37页直线与平面垂直的性质定理;
2.思考除了线面平行、线面垂直,在空间里我们还可以进行哪些研究?
综上所述,以问题引领导学四环节教学模式,以问题导入为中心创设情境,对于培养学生运用数学的眼光去发现问题,分析问题和解决实际问题的能力具有非常重要的意义。同时,运用这样的教学方法更加有利于培养学生的数学综合核心素养。
参考文献:
[1]余文森.从三维目标走向核心素养[J].华东师范大学学报,2016(01):11-13.
[2]黄建财.高中数学核心素养的培养、评价与教学实施[J].高考教育探索,2018,5(175).
[3]洪燕君.《普通高中数学课程标准(修订稿)》的意见征询——访谈张奠宙先生[J].数学教育学报,2015,6(3):35-39.
[4]钱万会.基于数学核心素养的课堂教学研究.中学数学研究[J],2018,7(下):18-21.
(作者单位:常州市武进区横山桥高级中学,江苏 常州213119)