基于ABC-SMC回归算法具有观测噪声的AR(p)模型的参数估计
2021-08-05许淑婷郑斌斌李安水张慧增
许淑婷,郑斌斌,李安水,张慧增
(杭州师范大学数学学院,浙江 杭州 311121)
时间序列自回归(AR)模型参数估计是统计学中一个重要的研究课题,其估计方法已经日趋成熟,主要有格点搜索、Newton-Raphson方法、最陡爬坡法、极大似然估计等[1]方法以及贝叶斯统计框架下的马尔科夫链蒙特卡洛(MCMC)方法和近似贝叶斯计算(ABC)算法[2].然而当观测数据存在噪声时,如何对模型参数进行有效的估计更是具有理论意义和应用价值.
对于具有观测噪声的AR模型,1979年Sakai和Arase[3]使用补偿最小二乘法(CBLS)对其参数进行估计,在此基础上,郑卫星[4]提出了一种具有直接结构的(ILSD)改进最小二乘法, Mahmoudi和Karimi[5]提出了一种将逆滤波方程与Yule-Walker方程结合的方法(IFILS).2008年,Diversi等[6]利用误差不变(EIV)的概念来估计具有观测噪声的AR模型.2020年,Esfandiari等[7]提出了4种方法来估计具有观测噪声的AR模型:第一种方法旨在减少低阶Yule-Walker方程中观测噪声方差的破坏性影响,并以递归的方式估计参数;第二种方法将其看成约束最小二乘优化问题并找到最佳值,通过迭代算法确定观测噪声方差,然后估计参数;第三种是使用近似值,将未知参数的数量减少到仅两个参数,并以递归方式估计参数;最后一种是将观测噪声的方差估计为充分放大的自相关矩阵的最小特征值,并使用它来估计参数.以上方法或计算成本大、不易实现,或是在高阶情况下估计效果不佳.本文在贝叶斯统计的框架下,采用简单又易于实现的近似贝叶斯序贯蒙特卡洛(ABC-SMC)回归算法来估计具有观测噪声的AR模型的参数.
近似贝叶斯计算(ABC)[8]是近年来贝叶斯统计推断中常用的方法.当模型比较复杂,似然函数难以写出具体表达形式时,利用ABC算法模拟参数近似后验分布的样本进而得到参数估计.1984 年Rubin[9]提出了ABC基本思想,2002 年Beaumont等[10]提出了最基本的ABC拒绝采样算法,基本ABC算法的缺点是当待估参数的维数比较大时计算成本很大,并且当模型具有噪声时,可能导致估计效率低下.2007年Sisson等[11]首次将粒子滤波器融入ABC方法,粒子滤波器[12]能从不完整的或者是含有噪声的观测序列中估计出动态系统的状态,从而提升估计效率.2009年Toni等[13]在处理动态系统问题时引入了序列重要性采样(SIS),提出ABC序贯蒙特卡洛算法.然而对于不同的采样粒子而言,生成的模拟数据集与观测数据集的差异程度是不同的,为此我们引入回归模型对采样结果进行调整,形成ABC-SMC回归算法.
本文内容组织如下:第1节介绍了具有观测噪声的AR模型及其自协方差函数;第2节阐述了具有观测噪声的AR模型的ABC-SMC算法.最后通过数值模拟,并与ABC算法、ABC-SMC算法进行了比较.模拟结果表明,所提出的ABC-SMC回归算法显著提高了具有观测噪声的AR模型参数估计精度.
1 具有观测噪声的AR(p)模型
定义1设{Yt:t∈T}为一时间序列,其中T=0,±1,±2,…,如果对于∀t∈T,有
其中{εt:t∈T}和{νt:t∈T}为均值为0,方差分别为σ和ν的高斯白噪声序列,且{Xt}和{νt}相互独立,则称{Yt}为具有观测噪声的AR(p)模型.
1.1 具有观测噪声的AR(p)模型的自协方差函数
命题1假设{Xt:t∈T} 为宽平稳的中心化AR(p)过程,令γX(0)=Var(Xt),γX(h)=Cov(Xt,Xt-h),h=±1,±2,…,则
1){Yt:t∈T}为宽平稳过程;
2)令γY(0)=Var(Yt),γY(h)=Cov(Yt,Yt-h),h=±1,±2,…,则γY(0)=γX(0)+ν,γY(h)=γX(h),h=±1,±2,….
证明由{Xt:t∈T}是宽平稳的中心化AR(p)过程,可知E(Xt)=0,则
E(Yt)=E(Xt+vt)=E(Xt)+E(vt)=0.
(1)
由{Xt}和{νt}相互独立,则对于∀t,τ∈T,t≠τ,有E(Xtvτ)=E(Xt)E(ντ)=0.由{νt}是高斯白噪声序列,可知
因此,{Yt:t∈T}的方差为
Var(Xt)+ν=γX(0)+ν,
(2)
并且当h=±1,±2,…时,有
Cov(Yt,Yt-h)=E(YtYt-h)=E(Xt+vt)(Xt-h+vt-h)=E(XtXt-h+Xtvt-h+Xt-hvt+vtvt-h)=
E(XtXt-h)=Cov(Xt,Xt-h)=γX(h).
(3)
由式(1)、(2)、(3)可知,{Yt:t∈T}是宽平稳的.由式(2)可知,γY(0)=γX(0)+ν;由式(3)可知,γY(h)=γX(h),h=±1,±2,….
注以下讨论的 {Xt:t∈T} 均为宽平稳的中心化AR(p)过程.
命题2对于具有观测噪声的AR(p)模型 {Yt:t∈T},自协方差函数满足:
1)γY(0)=φ1γY(1)+φ2γY(2)+…+φpγY(p)+σ+ν;
2)γY(h)=φ1γY(h-1)+φ2γY(h-2)+…+φpγY(h-p)-φhν,h=1,2,…,p;
3)γY(h)=φ1γY(h-1)+φ2γY(h-2)+…+φpγY(h-p),h=p+1,p+2,….
证明由{Xt:t∈T}为宽平稳的中心化AR(p)模型可知,{Xt:t∈T}的自协方差函数满足以下关系:
由命题1可得
γY(0)=γX(0)+ν=φ1γX(1)+φ2γX(2)+…+φpγX(p)+σ+ν=
φ1γY(1)+φ2γY(2)+…+φpγY(p)+σ+ν.
当h=1,2,…,p时,
γY(h)=γX(h)=φ1γX(h-1)+φ2γX(h-2)+…+φpγX(h-p)=
φ1γX(h-1)+φ2γX(h-2)+…+φhγX(0)+φh+1γX(-1)+…+φpγX(h-p)=
φ1γY(h-1)+φ2γY(h-2)+…+φh(γY(0)-ν)+φh+1γY(-1)+…+φpγY(h-p)=
φ1γY(h-1)+φ2γY(h-2)+…+φpγY(h-p)-φhν.
当h=p+1,p+2,… 时,
γY(h)=γX(h)=φ1γX(h-1)+φ2γX(h-2)+…+φpγX(h-p)=
φ1γY(h-1)+φ2γY(h-2)+…+φpγY(h-p).
1.2 具有观测噪声的贝叶斯AR(p)模型
1.2.1 具有观测噪声的AR(p)模型的似然函数
设{Yt:t∈T}为一具有观测噪声的AR(p)模型,记 Φ=(φ1,…,φp) 为模型系数.令y1:n为{Yt:t∈T}的可观测样本,x1:n为{Xt:t∈T}的不可观测样本,其中1:n表示1,2,…,n.那么y1:n,x1:n的似然函数为
p(y1:n,x1:n|Φ,σ,ν)=p(y1:n|x1:n,Φ,σ,ν)p(x1:n|Φ,σ,ν),
样本y1:n的似然函数为
1.2.2 具有观测噪声的AR(p)的参数先验分布
记I(λ)=λp-φ1λp-1-…-φp=0 是AR(p)模型 {Xt:t∈T} 的特征方程, Λ=(λ1,…,λp) 为该特征方程的特征根.众所周知, AR(p) 模型平稳当且仅当 |λi|<1,i=1,2,…,p.
令特征多项式因式分解如下:
防治适期掌握在发生高峰期前,且田间若虫占总虫量80%以上。无公害茶园用高效、低毒、低残留的2.5%高效氯氟氰菊酯微乳剂 1 500 克/公顷、25%噻虫嗪水分散粒剂50克/公顷进行防治;有机茶园则选用生物药剂0.3%苦参碱水剂4.5~9.0克/公顷[4]、30%茶皂素水剂30%茶皂素水剂60毫升/公顷[5]。采用低容量蓬面喷雾施药。
λp-φ1λp-1-φ2λp-2-…-φp=(λ-λ1)(λ-λ2)…(λ-λp).
(4)
式(4)右边展开得到
与式(4)左边比较有如下关系:
由此可知, AR(p)模型的模型系数φ1,φ2,…,φp由特征根λ1,λ2,…,λp唯一确定.
为了书写方便,我们将模型系数与特征根的关系记为 Φ=f(Λ).
由于在高阶情况下,难以刻画 AR(p) 模型的平稳域,可由根与系数的关系,将对模型系数Φ的估计转换成对特征根 Λ 的估计.因此在贝叶斯统计的框架下,具有观测噪声的AR(p)模型的待估参数为Λ,σ和ν.假设Λ,σ,ν相互独立,通常我们选取σ的先验分布为逆Gamma分布IG(ασ,βσ),ν的先验分布为逆Gamma分布IG(αν,βν),其中超参数ασ,βσ,αν,βν均为已知.
特征方程I(Λ)=0既有实根也有复根,且复根以共轭的形式成对出现.若{Xt:t∈T}平稳,则特征根的模小于1.若特征根的先验分布为复平面单位圆上连续型分布,则特征根为实根的概率为0,显然这是不合理的.本文对于特征根先验分布构造思想如下:首先定义共轭复根的对数为均匀分布,在共轭复数对数已知的条件下,遵循先验分布简单的原则,先在上半单位圆内按照均匀分布取复根,并确定其共轭复根,然后在区间(-1,1)上按照均匀分布对实根进行抽样.下面我们给出Λ先验分布的表示.


当k=0时,令λi~U(-1,1),i=1,2,…,p,且λ1,λ2,…,λp相互独立.则有Λ=λ1:p的条件分布如下:
故参数 Λ 的先验分布为
1.2.3 具有观测噪声的AR(p)模型的参数后验分布
假设具有观测噪声的AR(p)模型的参数先验分布为π(Λ),π(σ),π(ν).由1.2.1有y1:n,x1:n的似然函数为
p(y1:n,x1:n|Λ,σ,ν)=p(y1:n|x1:n,f(Λ),σ,ν)p(x1:n|f(Λ),σ,ν),
样本y1:n的似然函数为
则有模型的联合分布为
p(y1:n,Λ,σ,ν)=p(y1:n|Λ,σ,ν)π(Λ)π(σ)π(ν).
由贝叶斯公式可知,具有观测噪声的AR(p)模型的参数后验分布为
由于模型参数的后验分布无法给出具体的表达形式,下面我们通过给出参数后验分布的ABC-SMC抽样算法和ABC-SMC回归抽样算法,给出后验分布的估计.
2 具有观测噪声的AR(p)模型的贝叶斯估计
在本节中我们首先使用ABC-SMC算法对参数后验分布进行抽样,然后引入回归模型对抽样进行调整,本文把该算法称为ABC-SMC回归算法.
2.1 具有观测噪声的AR(p)模型的ABC-SMC算法
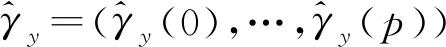
算法1Λ 的先验分布抽样算法
输入:模型的阶数p.
输出:生成Λ的随机向量.
算法步骤:

1.生成k~U{0,1,2,…,p2}.2.if k=0 then3.生成λi~U(-1,1),i=1,2,…,p.4.end if5.if k>0 then 6.生成λ'i~U(D),i=1,2,…,k.7.令λ2i-1=λ'i,i=1,2,…,k.8.令λ2i= λ'i,i=1,2,…,k.9. end if 10.生成λi~U(-1,1),i=2k+1,…,p. 11.输出Λ=λ1:p.
ABC-SMC算法基于蒙特卡洛方法,引入了序贯重要性采样方法.在ABC-SMC算法中,每次采样不再是一个样本,而是预定数量的样本N,每个样本称为粒子,一次采样的样本序列称为“粒子池”.对于粒子池中的每个粒子,设定扰动核q(·|·)进行扰动,再判断其是否满足所设定的条件,以此选择接受或拒绝.对接受的粒子进行赋权,以此权重进行下一次采样,生成新一代的粒子池.
对于具有观测噪声的AR(p)模型,由于Λ,σ,ν,相互独立,因此模型参数的先验分布为
π(θ)=π(Λ)π(σ)π(ν).


算法2Λ的扰动算法
输入:当前参数Λ(t)=λ1:p;当前共轭复数对数k.
输出:扰动后的参数Λ*.
算法步骤:
1.ifk=0 then
2.k*=1.


5.生成λ*~U(D).

7.end if

9.生成k*~U{k-1,k+1}.
10.ifk*=k-1 then
11.抽取I~U{1,2,…,k}.

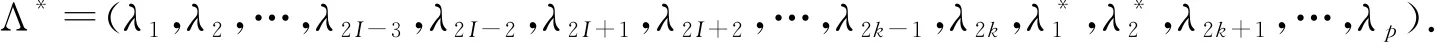
14.end if
15.ifk*=k+1 then


18.生成λ*~U(D).
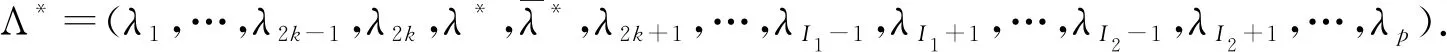
20.end if
21.end if

24.抽取I~U{1,2,…,k}.

26.ifp为奇数 then
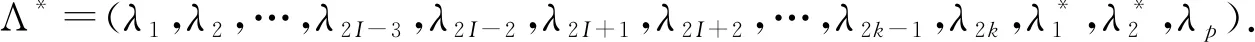
28.else

30.end if
31.end if
令k为Λ的共轭复数的对数,k*为Λ*的共轭复数的对数.由算法2可知,当k*=k-1 时,
当k*=k+1时,
设参数σ的扰动核为q(σ*|σ,ησ)=N(σ,ησ).参数ν的扰动核为q(ν*|ν,ην)=N(ν,ην).为了保证扰动得到的σ,ν均大于等于0,先扰动得到σ*和ν*,直至满足条件为止.下面是参数σ,ν的扰动算法.
算法3σ,ν的扰动算法
输入:当前参数σ(t),ν(t).
输出:扰动得到的下一代参数σ(t+1),ν(t+1).
算法步骤:

1.repeat 2.σ*~q(·|σ(t),ησ).3.until σ*>04.repeat5.ν*~q(·|ν(t),ην). 6.until ν*>07.输出 σ(t+1)=σ*,ν(t+1)=ν*.
令θ*=(Λ*,σ*,ν*),θ=(Λ,σ,ν).由算法2和算法3可得
q(θ*|θ)=q(Λ*|Λ)q(σ*|σ,ησ)q(ν*|ν,ην).


(5)
下面给出具有观测噪声的AR(p)模型的ABC-SMC算法.
算法4ABC-SMC算法
输入:观测数据集y∈Rn;模型阶数p;先验分布π(θ);超参数ασ,βσ,αν,βν;距离函数d(·,·);扰动核函数q(·|·);容忍度δ>0;粒子池数目N;迭代次数T.
算法步骤:

2.fori=1 toNdo
4.end for
6.fort=1 toTdo
7.fori=1 toNdo
8.repeat
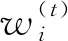
10.ifπ(θ**)≠0 then
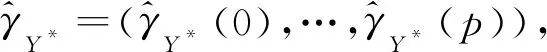
12.end if
13.untild(s,S*)≤δ

15.end for
17.end for
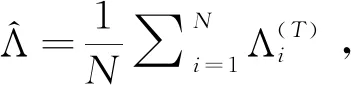
2.2 具有观测噪声的AR(p)模型的ABC-SMC回归算法



(6)

算法5ABC-SMC回归算法
输入:观测数据集y∈Rn;模型阶数p;先验分布π(θ);超参数ασ,βσ,αν,βν;Rp+1上距离函数d(·,·);扰动核函数q(·|·);容忍度δ>0;粒子池数目N;迭代次数T.
算法步骤:
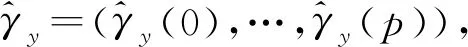

3.由式(6)定义X,Θ.



7.fori=1 toNdo

9.end for
3 数值模拟
为了说明以上方法的有效性,下面给出如下数值模拟.
假定模型为
先由模型随机地生成观测数据集y1,…,yn;取样本量n=1 000,超参数ασ=1,βσ=0.3,αν=1.2,βν=0.5,粒子池数目为N=100,迭代次数T=1 000,容忍度δ=3,参数的扰动核方差ησ=ην=0.1;分别使用ABC-SMC算法以及ABC-SMC回归算法对参数后验分布进行抽样,计算样本均值作为参数的估计值,并与ABC算法进行比较.为了观察先验分布选取对模拟结果的影响,再取先验分布σ~Exp(0.5),ν~Exp(0.8)进行模拟,并与前面的估计结果比较.
以下图1、 图2和 图3分别为ABC算法、 ABC-SMC算法以及ABC-SMC回归算法抽样所得的参数近似后验分布结果,实曲线为核密度估计,实直线表示真实值,虚线表示估计值.其估计值以及估计相对误差的比较见表1.由表1可以看出,ABC-SMC算法的估计精度比ABC算法高很多,而引入回归之后的ABC-SMC回归算法估计效果有显著提升.表2为不同先验分布的模拟结果.由表2可以看出,不同的先验分布均能将估计误差控制在10%以内,说明先验分布的选取对模拟结果的影响不大.
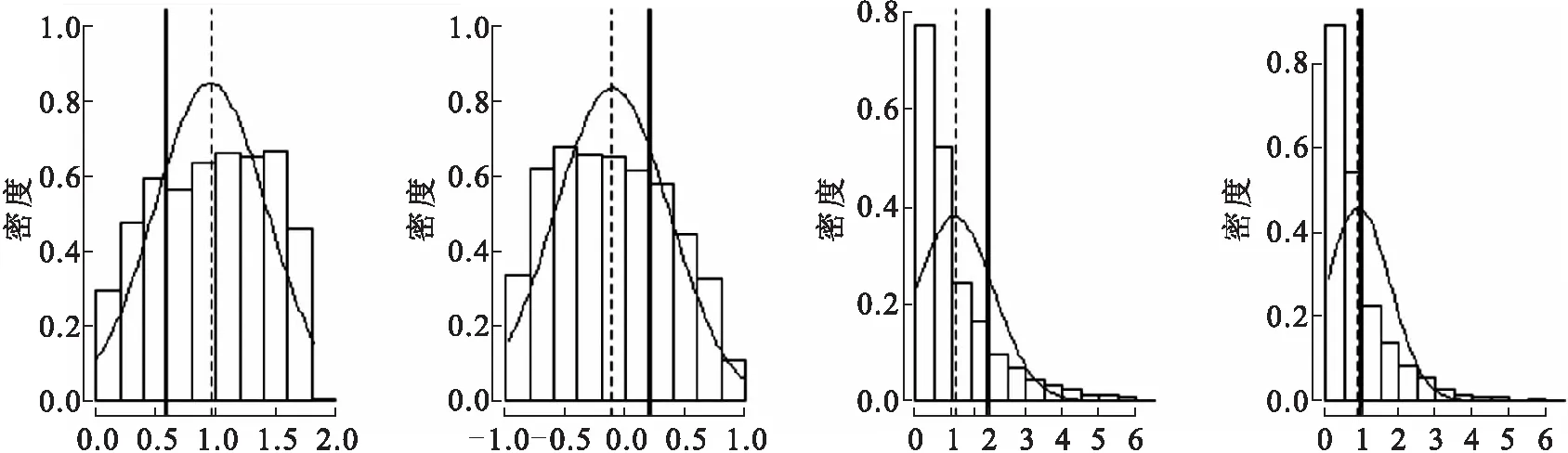
φ1 φ2 σ υ
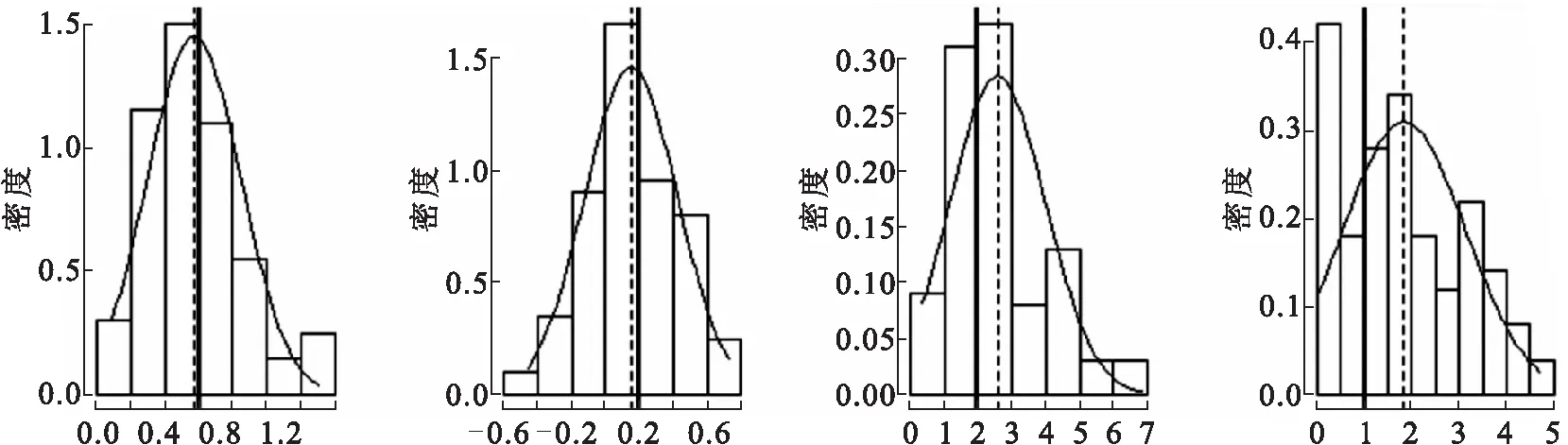
φ1 φ2 σ υ

φ1 φ2 σ υ

表1 ABC算法、ABC-SMC算法和ABC-SMC回归算法估计结果对比

表2 ABC-SMC回归算法选取不同先验分布的估计结果对比
4 结论
对于具有观测噪声的AR(p)模型,采用前p阶样本自协方差函数作为统计量,使用ABC-SMC算法对其参数进行估计是有效的;在此基础上引入回归模型调整采样结果后,估计精度有显著提升.
