仓内拣货路程优化问题研究

谢晓敏，李 琳

（川北幼儿师范高等专科学校 初等教育系，四川 广元 628017）

1 问题的提出

随着物流业的迅速发展，越来越多的企业构建属于自己的仓储体系。在整个仓储体系中，拣货作业是其核心，且涉及的计算复杂。因此，拣货作业的优化设计与综合控制至关重要。某电商公司的双区型[1]仓库中有13个复核台，4排（行）货架，每排25组货架，每组2个货架，共200个货架，每个货架包含15个货格。货架与复核台分布如图1所示。相邻货架间的垂直过道宽1 500 mm，水平过道宽2 000 mm，货格长宽均为800 mm，复核台长宽均为1 000 mm。13个复核台用F01～F13标记，其中：F01～F08在最下面，处于同一行，从左至右排列，横坐标以4 500 mm的量增加；F09～F13在最左面，处于同一列，从下至上排列，纵坐标以4 500 mm的量增加。每个货架中的15个货格从下至上纵向排列。图2为1号、2号货架上货格的分布情况，其中字母S代表“货格”，数字编号的前三位表示货架号，后两位表示货格号。3000个货格和13个复核台的左下角坐标都已给定。货架和复核台为障碍物，不可通行，其余位置均可通行，不用考虑拣货车尺寸、货架和复核台高度。当拣货员在仓库中拣货时，要在货格与复核台之间行走，通常需绕过障碍物，不能直接采用坐标计算欧几里得路程[2]。要求设计一种方法，计算3 000个货格和13个复核台（共3 013个元素）之间的最短路程，并满足如下要求：

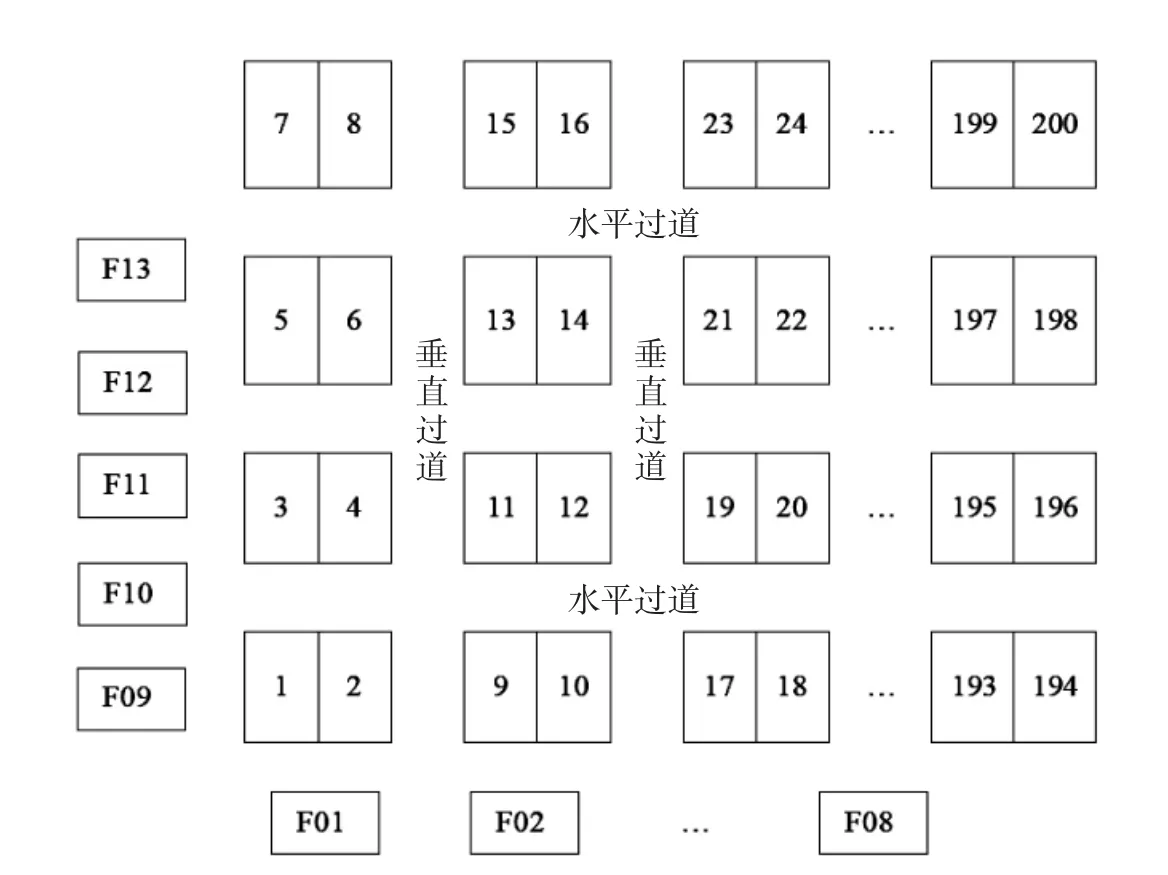
图1 货格与复核台的分布

图2 货架上货格的分布

（Ⅰ）当绕障碍物折线行走时横向和纵向偏移均取d=750 mm；

（Ⅱ）奇数号货架上的货格从左边中点出发，偶数号货架上的货格从右边中点出发；

（Ⅲ）复核台F01～F08的出发点是上边中间位置，复核台F09～F13的出发点是右边中间位置。

2 标识点及其坐标变换

编号为n的货格标记为S n，五位数n的前三位表示其所在的货架号，记作i（n），也可用算式表示为

如图3所示，从货格S n的边线中点出发，先要偏移距离d=750 mm，偏移后的点Bn称为S n的标识点，An为给定原始坐标的点。

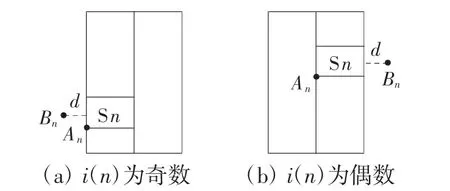
图3 货格的标识点

将所有货格的原始纵坐标都加400 mm；当i（n）为奇数时，将货格S n的原始横坐标减d；当i（n）为偶数时，将货格S n的原始横坐标加（d+800）mm。经坐标变换得到货格标识点Bn的坐标，记为（xn，yn）。

如图4所示，编号为j的复核台标记为F j（j=01~13），字母F代表“复核台”。F j也有标识点，记做Qj，Pj为给定原始坐标的点。

图4 复核台的标识点

当j=01~08时，将F j的原始纵坐标加（d+1 000）mm，原始横坐标加500 mm；当j=09~13时，将F j的原始纵坐标加500 mm，原始横坐标加（d+1 000）mm。经坐标变换得到复核台标识点Qj的坐标，记为（Xj，Yj）。

引入标识点及其坐标，可消弭奇数号货架上货格与偶数号货架上货格偏移方式的差异，同时也消除了横排复核台与纵列复核台偏移方式的差异，大大降低了计算的复杂程度，使得所建模型简洁明了。

因为要绕过障碍物，有时需在货架下方或上方的水平过道行走，所以还要引入货格S n所在货架的下沿纵坐标gn和上沿纵坐标hn。gn等于该货架第1个货格（最下方货格）的原始纵坐标，而hn=gn+2c，2c=15×800＝12 000 mm是货架的纵向长度，gn和hn都是已知数据，共只有4对不同的数值。

3 问题的求解

3013个元素之间的路程存储在路程矩阵中，该矩阵是一个方阵，对角线上元素都为0，对称位置的元素相等，总共有9 078169个元素。由于数量庞大，需分成货格与货格、货格与复核台、复核台与复核台三个部分来求解[3]。

3.1 货格与货格之间的路程计算

货格S m与货格S n（m≠n）之间的路程用dmn表示。当S m与S n所处货架不同行时，其标识点Bm和Bn之间有水平过道，无须绕行，如图5所示。计算dmn只需先算得Bm和Bn之间的路程，再加上图中的虚线段偏移即可：

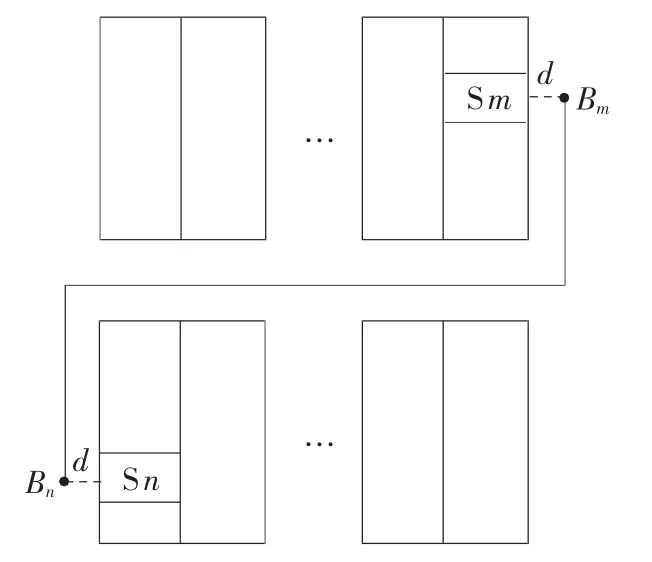
图5 不同行货架中货格之间的路径

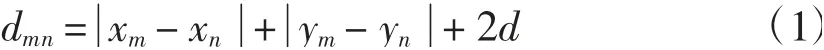
若S m与S n所处货架虽在同行，但它们的标识点处于同一垂直过道，则无须借助水平过道行走，dmn仍可按式（1）计算，例如S00202和S00913、S01312和S01303、S01605和S01614等等。

若S m与S n所处货架在同行，且标识点Bm和Bn未处于同一垂直过道，则行走路线需经货架下方或上方绕行，如图6所示。路程计算取下行路程d′mn和d″mn上行路程中的较小者，即：

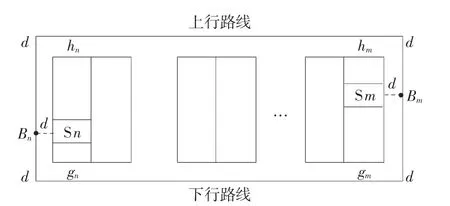
图6 同行货架中不共过道货格之间的路径

其中：d′mn=xm-xn+（ym-gm）+（yn-gn）+4d，d″mn=xm-xn+（hm-ym）+（hn-yn）+4d，并且对于同行货架的上、下沿，有gm=gn，hm=hn。

3.2 货格与复核台之间的路程计算

货格S n与复核台F j间的路程用dnj表示。

当j=01~08时，复核台F j处于所有货格的下方，标识点Bn和Qj之间必有水平过道，无须绕行，路程计算可仿照式（1），有：

3.3 复核台与复核台之间的路程计算

复核台F j与复核台F k（j≠k）之间的路程用djk表示。由于标识点Qj和Qk之间总有水平过道或者处于同一垂直过道，所以路程计算可仿照式（1），有：

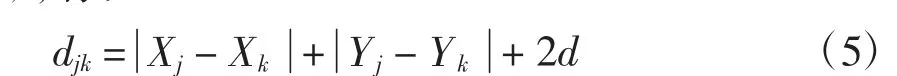
4 模型的评价与推广

模型通过针对性的坐标变换，引入标识点并进行分类归纳，大大降低了复杂距离的计算难度。

本文的坐标变换方法和路程计算方法在拣货模型[4]和路径问题中都可以应用，能有效降低拣货路径分析的复杂程度。