超超临界机组全负荷段机炉协调系统建模研究

高 峥，吕剑虹，屈小凡，葛 浩

(东南大学 能源与环境学院，南京 210096)

随着电网清洁能源增加，以及全社会用电需求增速放缓，使得电网峰谷差越来越大，在保证清洁能源不弃风弃光的情况下火电机组调峰任务越来越突出。因此，提升火电机组运行灵活性，使其大规模参与电网深度调峰将是大势所趋。

国内外在协调系统建模方面的研究有很多，LIU J Z等[1-2]在文献[3]的基础上，通过合理简化和机制分析，根据质量、能量和动量平衡方程建立适用于直流炉机组协调控制系统控制器设计的简化非线性数学模型，该模型结构简单，具有一定的实用性。陈宝林等[4]利用最小二乘法建立了协调系统的模型，该模型在某个负荷点上的模拟结果精确，但不适用于大范围工况变化的情况，运用神经网络模型进行改进，模拟结果的精度明显提高。韦根原等[5-6]运用粒子群算法分别建立了350 MW超临界机组和1 000 MW超超临界机组的传递函数模型，提高了辨识的精确性与快速性。

深度调峰负荷变化范围较广，目前的建模研究大多集中在干态情况下，为了进一步了解湿态下的机组运行动态特性，同时在模型基础上研究深度调峰下的新型协调控制方法，需要建立能够正确反映机组中各设备参数的变化，以及机组动态响应的全负荷段非线性模型。笔者以国内某1 000 MW超超临界机组为研究对象，由于锅炉和汽轮机中汽水系统复杂，对工质采用移动边界建模实施难度大，所以采用分段集总参数法建立非线性模型，采用教与学算法计算模型中的参数，通过与现场实际数据仿真验证，证明了该模型具有一定应用价值。

1 全负荷段非线性模型

1.1 模型结构及假设

超超临界机组的协调系统主要包括锅炉燃烧系统、汽水系统和汽轮机系统三部分。锅炉燃烧系统为煤通过磨煤机制粉后进入锅炉燃烧，汽水系统包括省煤器、水冷壁、过热器和再热器。给水先后进入省煤器、水冷壁加热后经汽水分离器将蒸汽分离，分离出的蒸汽进入过热器进一步加热，产生的高温高压蒸汽进入汽轮机系统高压缸做功，高压缸排汽经过再热器加热后进入中低压缸做功。

对于超超临界机组的协调系统建模，一般输入量为给水流量、给煤量和汽轮机调节阀开度，需要求解中间点温度(汽水分离器出口蒸汽温度)、主蒸汽压力、主蒸汽温度和机组功率。往常的干态模型若应用于全工况下湿态模型有较大的误差，误差来源为：(1)机组在低负荷段时，汽水分离器出口带水，机组进入湿态，汽水分离器中一部分流量经过再循环回到水冷壁，在干态下的质量平衡方程将不准确；(2)水冷壁和过热器由于吸热特性不同，吸热量比例发生变化，从而导致汽水分离器出口参数发生变化；(3)当机组在低负荷段时进入湿态，汽水分离器储水罐的水位也应作为输出量。因此，需要建立适合干态和湿态的全负荷段模型。笔者首先对真实系统进行适当简化：锅炉段模型将省煤器和水冷壁简化为一根均匀受热的管道，吸热量为Q1；将过热器单独简化为一根均匀受热的管道，吸热量为Q2。简化后锅炉模型结构见图1。

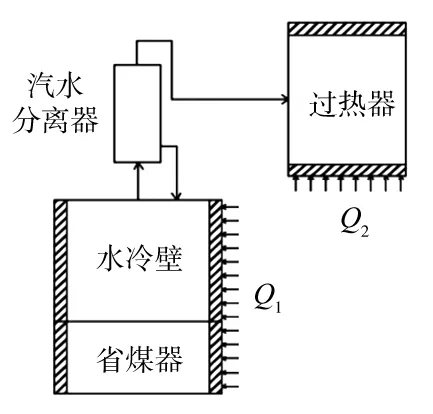
图1 锅炉段简化模型

对简化后的锅炉模型进行以下假设：

(1)假定省煤器-水冷壁、过热器的金属温度与工质温度相同，且金属温度与工质温度同步变化。

(2)将汽水分离器和储水罐简化为一个圆柱形容器。

(3)忽略汽水分离器内工质旋流对能量损失的影响。

(4)忽略汽水分离器散热对能量损失的影响。

(5)假定汽水分离器内部工质分布均匀且分离效率为1。

由此简化后的协调系统可分为锅炉部分和汽轮机部分，锅炉部分又分为锅炉燃烧过程、省煤器-水冷壁吸热过程、过热器吸热过程3个过程以及汽水分离器1个中间环节，采用出口参数作为集总参数。

1.2 全负荷段模型建立

1.2.1 锅炉部分

(1)锅炉燃烧过程。

锅炉燃烧过程采用文献[7]中所建模型的制粉过程和燃烧放热，计算公式为：

(1)

Qb=μbqm,b

(2)

式中：qm为给煤质量流量，kg/s；qm,b为煤粉质量流量，kg/s；s为复参数，t0为惯性时间，s；τ为纯延迟时间，s；Qb为锅炉总放热量，kJ/s；μb为煤燃烧热值,kJ/kg。

(2)省煤器-水冷壁吸热过程。

为进一步简化模型，假设：忽略烟气侧的动态过程；烟气侧向管侧传热是强制传热；忽略管长方向的轴向传热。考虑管内工质的密度变化带来的流量变化，以及金属的蓄热量，则工质的质量平衡方程和能量平衡方程为：

(3)

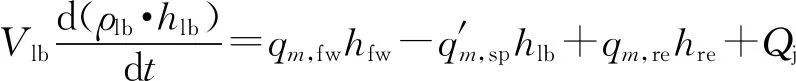
(4)

式中：t为时间，s；Vlb为省煤器-水冷壁管内体积，m3；ρlb为省煤器-水冷壁出口工质密度，kg/m3；qm,fw为给水质量流量,kg/s；q′m,sp为汽水分离器进口工质质量流量，kg/s；qm,re为再循环水质量流量；kg/s；hlb、hfw和hre分别为省煤器-水冷壁出口工质焓、给水焓和再循环水焓,kJ/kg；Qj为省煤器和水冷壁的金属吸热量，kJ/s。

而省煤器-水冷壁的金属吸热量的一部分传递给管内工质，另一部分用于自身蓄热，因此其能量平衡方程为：

(5)

(6)

式中：k为传热系数，W/(cm2·K)；Qlb为省煤器-水冷壁吸热量，kJ/s；Tj为省煤器-水冷壁的金属壁温,℃；cj为金属比热容,kJ/(kg·K)；mj为省煤器-水冷壁的金属质量,kg。

由于省煤器-水冷壁出口工质焓hlb即为汽水分离器进口工质焓hsp，将其作为状态变量，对式(3)和式(4)整理可得：

(7)

qm,fwhfw-q′m,sphlb+qm,rehre+Qj

(8)

令a1=2Vlb(∂ρlb/∂hsp)，a2=2Vlbρlb，将式(7)代入式(8)并将式(6)代入式(5)可得省煤器-水冷壁部分模型：

(9)

省煤器-水冷壁出口工质密度ρlb等于汽水分离器进口工质密度ρsp，a1为待辨识的动态参数。

(3)汽水分离器环节。

对汽水分离器建模主要是为了在机组进入湿态时得到再循环水流量和汽水分离器储水罐水位，因此对汽水分离器列出质量和能量平衡方程。

质量平衡方程为：

(10)

式中：Vsp为汽水分离器中工质体积，m3；q″m,sp为汽水分离器出口蒸汽质量流量，kg/s。

由汽水分离器储水罐水位H和汽水分离器截面积F可得：

Vsp=Vw+Vi=HF+Vi

(11)

式中：Vw和Vi分别为汽水分离器中水和蒸汽的体积,m3。参照式(8)单独对Vw部分列质量平衡方程可得汽水分离器储水罐水位变动方程为：

(12)

式中：ρw为饱和水密度，kg/m3；x′为汽水分离器进口工质干度。

能量平衡方程为：

q′m,sph′sp-q″m,sph″sp-qm,rehre

(13)

式中：hw为饱和水焓，kJ/kg；ρi为饱和蒸汽密度，kJ/kg；hi为饱和蒸汽焓，kJ/kg。

式(13)对汽水分离器出口压力psp求偏导并代入式(12)可得：

(14)

令b1=∂ρihi/∂psp,b2=∂ρwhw/∂psp,b3=∂Tj/∂psp，b1、b2、b3为待辨识的动态参数，式中ρw、ρi、hi和hw均可由psp得出，因此令g=(ρihi-ρwhw)/ρw=f(psp,hsp)，整理后汽水分离器模型为：

(15)

W=g(q′m,sp-q″m,sp-qm,re)

(4)过热器吸热过程。

主要研究协调系统部分的建模，故不考虑过热减温水的影响，由汽水分离器模型可得汽水分离器出口蒸汽压力，可根据动量方程得到主蒸汽压力：

(16)

式中：qm,st为主蒸汽质量流量,kg/s；pst为主蒸汽压力，MPa；λst为流动阻力系数；ρst为主蒸汽密度，kg/m3。由文献[7]可将式(16)简化为：

qm,st=k3(psp-pst)

(17)

式中：k3为待辨识参数。质量平衡方程和能量平衡方程与省煤器-水冷壁模型相似，以过热器出口参数为集总参数，进入过热器蒸汽质量流量为汽水分离器出口蒸汽质量流量q″m,sp，进入汽轮机蒸汽质量流量为主蒸汽质量流量qm,st，可得过热器段的质量平衡方程为：

(18)

式中：Vgr为过热器段管内体积，m3。

过热器段吸热量Qg由省煤器-水冷壁吸热比例klb可得，即Qg=(1-klb)Qb，因此过热器段能量平衡方程为：

(19)

式中：mg为过热器段金属质量,kg；Tg为过热器段金属壁温,℃。参考省煤器-水冷壁部分模型可得过热器部分模型：

(20)

式中：Tst为主蒸汽温度，℃。

1.2.2 汽轮机部分

对汽轮机部分，将汽轮机入口处的蒸汽流量和压力、温度的关系表示为：

qm,st=g(ut)f(pst,Tst)

(21)

式中：ut为汽轮机调节阀开度，%；g(·)、f(·)分别表示一种函数关系。文献[4]提出函数关系可以表示为：

(22)

式中：ttur为惯性时间，s，一般取10～20 s。在式(22)的基础上辨识函数k(ut)，假设k(ut)为多项式形式：

(23)

机组发电功率Ne可由能量平衡[2]计算得出：

Ne=k2qm,st(hst-hfw)

(24)

式中：k2为考虑机组发电效率的等效系数。

2 模型参数求取

2.1 静态参数计算

由上述建模结果可知，待辨识的参数有a1、b1、b2、b3、c1、c2、klb、k、k2和k3，共10个，klb和k2可根据表1数据静态辨识，另外制粉过程的时间常数t0和τ可以参考同类型磨煤机的取值[7]。

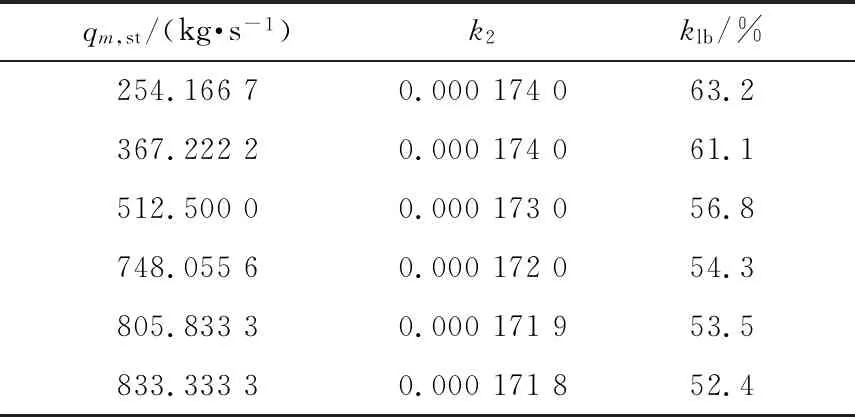
表1 模型静态参数

表1中qm,st和klb由国内某1 000 MW机组现场历史运行数据得到，因为省煤器-水冷壁金属质量与包括顶棚过热器、包覆过热器、一级过热器和二级过热器的过热器部分金属质量相近，因此可以近似认为省煤器-水冷壁吸热比例为工质在省煤器-水冷壁的吸热量与工质总焓升之比[8]。由表1可见：k2在随qm,st变化时变化不大，故取k2=0.001 73。klb经过测试采用有理函数逼近效果最佳，有理函数可写为：

(25)

式中：P(x)和Q(x)均为(ax-b)n的多项式，a和b为待拟合系数。利用MATLAB软件拟合工具箱拟合一次有理函数得到：

klb=(9.63qm,st+195 200)/(0.278qm,st+2 665)

(26)

2.2 动态参数计算

2.2.1 教与学算法

动态参数部分利用机组实际运行数据，通过教与学算法辨识。教与学算法与粒子群算法、遗传算法等同属于一种群智能优化算法，与其他群智能算法不同的是教与学算法不需要设置算法自身的计算参数，且简单易实现。

教与学算法中学生成绩Xi被当作种群中的第i个个体，学生各个科目的成绩作为待优化的解，科目的多少为待优化解的维度，最好的成绩作为老师成绩Tj，分为“教”和“学”两个阶段。

在教阶段，学生向老师学习，假设在第j次循环中，学生根据所有学生的平均成绩Pj与老师成绩之间的差距Dj进行学习，其中：

Dj=rj(Tj-R·Pj)

(27)

式中：rj为1到2之间的随机数；R代表学习作用的强弱，一般取1或2。此时学生根据平均成绩更新自身成绩：

Xi,j=Xi,j-1+Dj

(28)

若成绩优于更新前则接受更新，否则不更新。

在学阶段，学生之间相互学习，假设在第j次循环中，随机抽取一个学院成绩Xk,j进行学习：

Xi,j=Xi,j-1+n·rj(Xi,j-Xk,j)

(29)

式中：n为学习判断系数。如果Xk,j成绩优于Xi,j,则n=1,否则n=-1。同样检验更新后的成绩是否优于更新前，若优于更新前则接受更新，否则不更新。

2.2.2 参数计算

由于教与学算法本身基不需要参数设置，只需要对待辨识参数设置搜索范围，共有a1、b1、b2、b3、c1、c2、k和k38个参数需要辨识，搜索范围见表2。

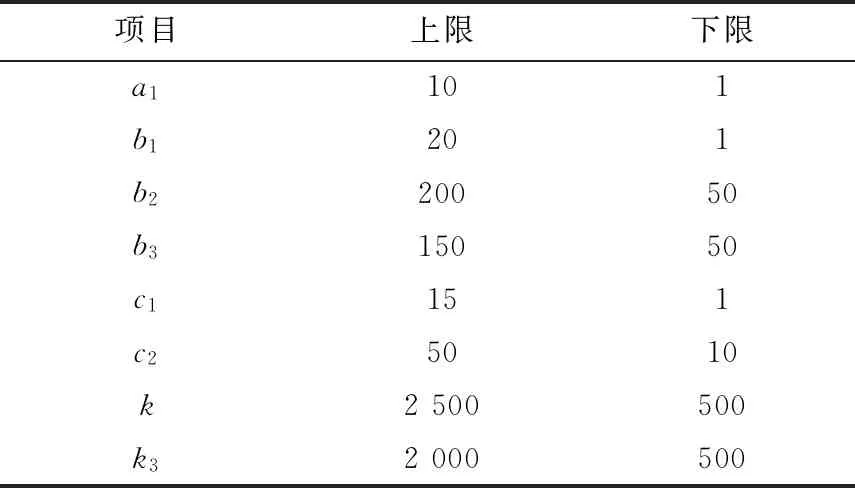
表2 待辨识参数搜索范围

算法适应度函数为：

(30)

式中：t1为仿真结束时间；Δ为模型计算值与现场实际值的差；下标0为现场实际值。F(x)越小表明模型与实际过程越接近，当算法达到迭代上限或已收敛，则停止迭代，得到最终的模型参数。

设置教与学算法种群数量为50，迭代上限为50次，利用国内某1 000 MW机组现场运行数据，输入给煤量、给水量、再循环水流量和汽轮机调节阀开度，得到计算结果见表3。

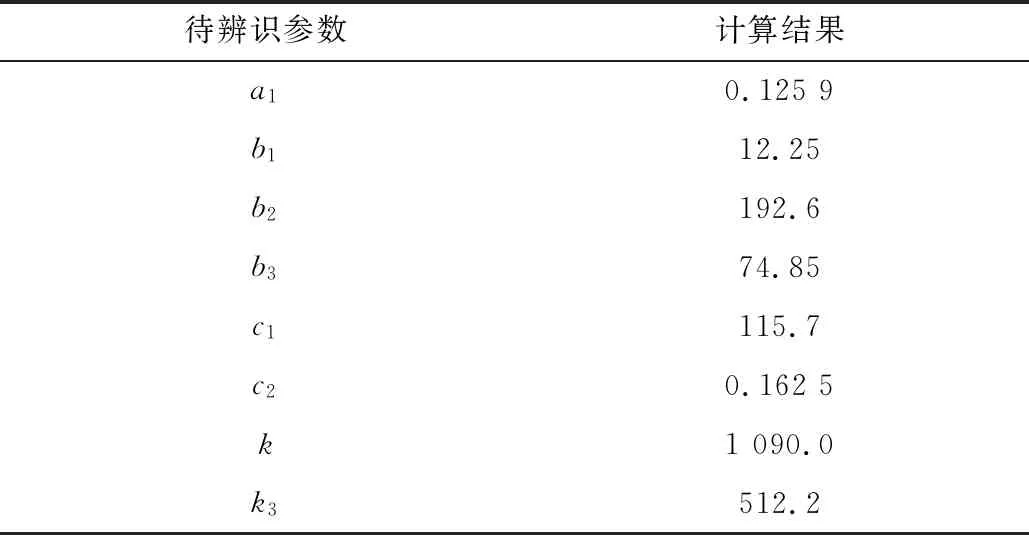
表3 待辨识参数计算结果

3 模型验证

利用现场机组降负荷时干态转湿态过程的数据对模型进行验证，0 s时机组实发功率为338 MW，给煤质量流量为120 t/h，进入省煤器的给水质量流量为1 066 t/h，主蒸汽压力为9.8 MPa。当实发功率为319 MW时机组由干态开始进入湿态。对比模型输入给煤量、给水量、再循环水流量和汽轮机调节阀开度,得到模型对比验证曲线见图2。

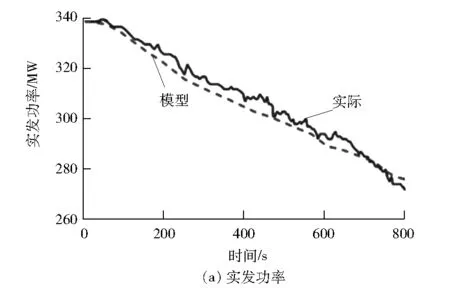
图2 干态转湿态模型对比验证曲线

由图2可得：模型对机组实发功率和主蒸汽压力的模拟比较准确；在储水罐水位方面，干态过程时，模拟值与实际值误差较小，而湿态过程在250 s开始水位有较大幅度上升，在610 s开始下降至稳定，这是因为再循环水流量增加使得模型输出水位出现较大变化，其中模型计算的水位变化速率较快，变化幅度较大，这是由于储水罐容积计算与实际存在偏差，惯性容积不同导致水位变化速率有差异；在汽水分离器出口焓方面，在干态和湿态的起始过程，模拟值和实际值的计算误差较小，在430 s后有一定偏差，其原因一方面是模型计算简化，忽略了散热等能量损失，另一方面是汽水分离器干度存在计算误差或分布不均，在功率变化过程中给水对主蒸汽压力的作用较快导致在湿态下模拟值与实际值有偏差。但总体上该模型可以正确反映机组变化状态并满足仿真的要求。

利用模型仿真机组湿态转干态的过程，0 s时机组实发功率为388 MW，给煤质量流量为176 t/h，进入省煤器的给水质量流量为1 100 t/h，主蒸汽压力为11.46 MPa，得到模型对比验证曲线见图3。

图3 湿态转干态模型对比验证曲线

从图3可以看出：湿态转干态过程的煤量变化与干态转湿态时相比变化较大，导致主蒸汽压力和实发功率发生振荡，主蒸汽压力最大偏差为0.06 MPa，实发功率最大偏差为5.4 MW，在整个振荡过程中模型输出与实际情况趋势基本一致，总体上模型输出比较准确。储水罐的实际水位与模型计算结果趋势一致，但模型的水位速率变化较快，理论分析水位在干态中应变为0 m水位，而实际水位在干态中仍留有一点水位，是由于水位已处于测量下限以下。在湿态转干态过程中，实际汽水分离器出口焓先下降后再上升，其原因可能是调节过程中实际水对主蒸汽压力的作用比煤快，实际汽水分离器热容与模型计算有偏差导致，在湿态转干态过程有一定幅度的下降。

结合图2和图3可得：该模型在干态过程比较准确，在湿态过程时有一定误差，但整体趋势是一致的，可以反映机组的运行状态，满足仿真的要求。

4 结语

随着对超超临界机组的深度调峰要求越来越高，在对超超临界模型的研究中，往常的干态模型应用于全工况下湿态模型有较大的误差，由于汽水分离器出口带水导致干态计算公式不再适用于湿态，需要重新建模。笔者提出的全工况协调系统模型，利用质量和能量平衡建立了省煤器-水冷壁、汽水分离器、过热器和汽轮机的非线性模型，针对模型中无法确定的参数，通过理论与经验相互结合的方式，基于历史数据，采用教与学的启发式算法进行确定。最后进行干态转湿态和湿态转干态过程的仿实验，仿真结果表明模型在干态和湿态能够较好地反映机组的特性，其中干态过程更为准确，湿态过程有一定误差。