基体表面粗糙度对HVOF 粒子沉积行为的影响
2021-08-03查柏林贾旭东王金金石易昂苏庆东曹晓恬许可俊
查柏林,贾旭东,王金金,石易昂,苏庆东,曹晓恬,许可俊
(1.火箭军工程大学,西安 710038;2.火箭军装备部装备项目管理中心,北京 100085)
HVOF 作为表面改性方法之一,相较于冷喷涂与等离子喷涂,其以高动能、低热能输出,广泛应用于耐磨、防腐、绝热涂层的制备[1-2]。WC-12Co 以其高熔点、高硬度、高耐磨性,广泛应用于机械零部件表面强化与修复[3-4]。45#碳钢以其高硬度、高强度,广泛应用于交通运输、机械制造、国防军工等领域[5-6],但是使用过程中的摩擦振动,会加剧45#碳钢材料的磨损失效。在45#碳钢表面制备WC-12Co 耐磨涂层,可以对45#碳钢实现有效保护,延长其使用寿命。研究结果表明[7],涂层制备实质上是喷涂粒子的沉积堆垛过程,而喷涂粒子与基体的结合行为将对粒子与基体的结合强度以及涂层的性能产生影响。因此,研究喷涂粒子的沉积行为对于提升涂层性能具有重要意义。
S. Gu 等[8]采用ABAQUS 软件,针对不同速度、温度、形状下的喷涂粒子在基体上的沉积行为进行了模拟计算。结果表明,粒子与基体的成功结合存在临界速度,低于临界速度,粒子将产生反弹剥落,并夯实基体。粒子初始温度或者速度越高,粒子扁平化程度越高,与基体结合越充分。非球形粒子相比球形粒子,需要更高的速度与温度,才能与基体结合。在文献[8]的研究基础上,S. Gu 等[9]还探讨了不同孔隙率的粒子的沉积变形行为。结果表明,粒子内的孔隙在扁平化过程中,逐渐由球形向线形发生转变,在一定范围内增加粒子孔隙率,不仅能够增加粒子的扁平化程度,而且可以促进粒子与燃气射流中的动量交换,获得质量更为优异的涂层。袁晓静、王汉功等[10]在单个粒子与基体碰撞的基础上,进行了双粒子沉积仿真研究。结果表明,后续粒子对已沉积粒子的撞击行为将引起已沉积粒子的二次变形,已沉积粒子的塑性变形将对基体产生粗化作用,降低后续粒子的临界沉积速度,有利于后续粒子的沉积。
综上,针对喷涂粒子的沉积行为,人们已进行了大量的数值模拟研究,但是研究内容多针对粒子与基体沉积前的状态参数对粒子沉积行为的影响,同时数值模拟过程均将基体表面理想平面化,忽略了基体表面粗糙度对粒子沉积行为的影响。实际喷涂作业过程中,不同基体表面粗糙度下,粒子-基体结合强度具有显著差异[11]。因此,深入研究基体粗糙度对粒子沉积行为的影响,对于改进涂层结构,提升涂层结合强度具有重要意义。
1 仿真模型
飞行粒子测速实验以及仿真研究结果表明[12]:超音速火焰喷涂粒子撞击速度通常可达400~800 m/s,粒子温度可达800~1500 K。粒子沉积过程中,接触区域将产生剧烈的塑性应变,发生物理结合,甚至冶金结合。因此,本文在非线性动力冲击背景下,使用LS-DYNA 软件,对不同表面粗糙度下45#碳钢基体上的WC-12Co 粒子沉积行为进行建模分析,计算结果综合考虑了粒子沉积过程中的应变强化、升温熔化、摩擦以及塑性功与热能之间的转化。
1.1 有限元撞击模型
超音速火焰喷涂实验使用具有良好耐磨性[13]的Metco-WOKA-3102 型WC-12Co 喷涂粉末,微观结构见图1。其形状近似为球形,具有良好的流动性,粉末粒径分布范围为15~45 μm。

图1 喷涂粒子形貌Fig.1 Morphology of spray particles
根据粒子与基体的几何与物理参数,建立二维超音速火焰喷涂WC-12Co 粒子与45#碳钢基体的撞击模型。图2 所示为Ra分别为2.51、5.34、10.26 μm时,基体表面形貌图以及横截面形貌波动图。由图可知,当Ra=2.51 μm 时,波峰-波谷最大深度差小于粒子半径;Ra=5.34 μm 时,波峰-波谷最大深度差介于粒子半径与粒子直径之间;Ra=10.26 μm 时,波峰-波谷最大深度差大于粒子直径,基体表面波动幅度显著增加,存在明显沟壑。

图2 不同表面粗糙度下基体表面形貌与横截面形貌波动曲线Fig.2 Fluctuation curves of surface morphology and cross section morphology of substrate under different surface roughness
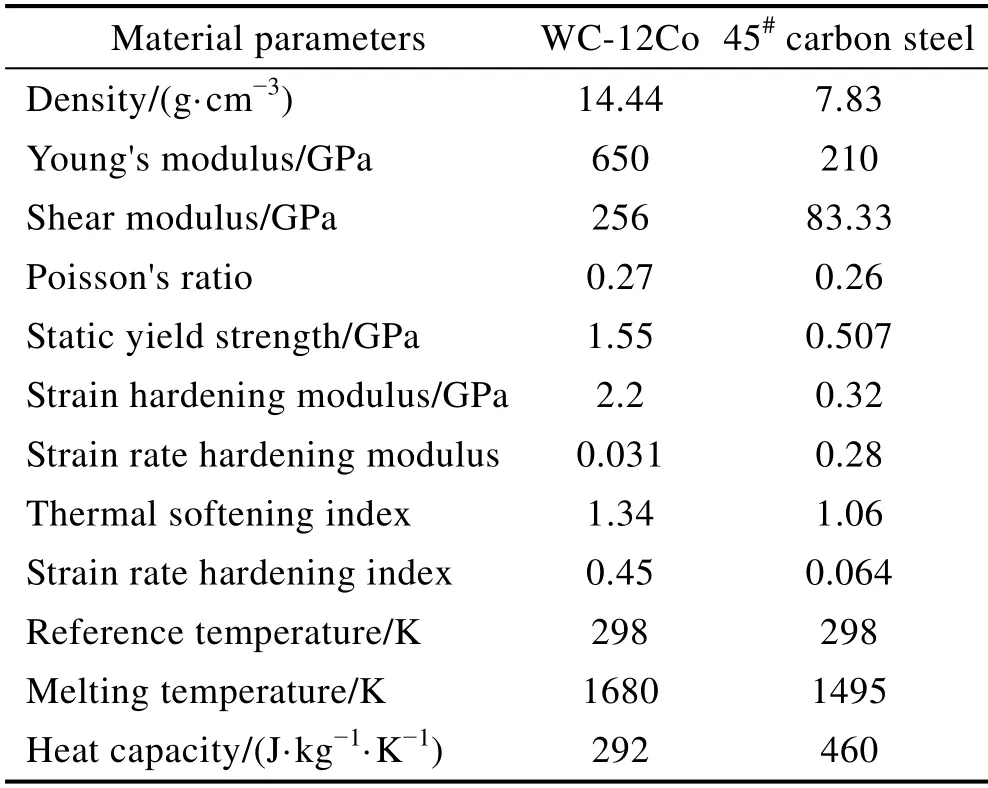
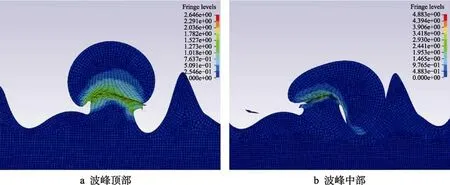
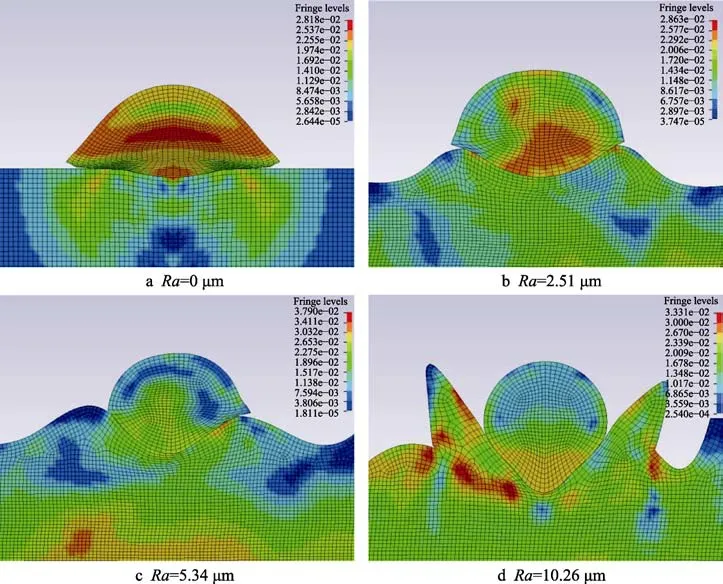
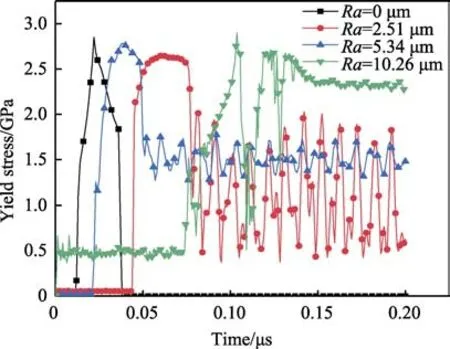
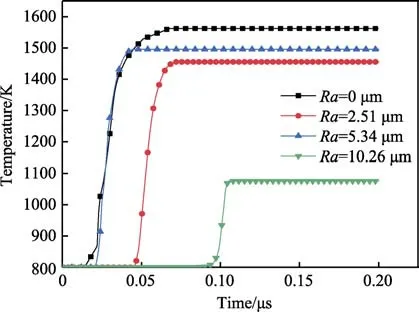
由于基体表面形状复杂多变,为降低模型复杂程度,对图2 所示的基体截面形貌波动进行简化处理,波峰与波谷均采用光滑曲线构成,基体表面无不规则折线存在,构建如图3 所示的不同表面粗糙度下的基体表面形貌。在图3 所示的计算模型中,WC-12Co粒子直径取粉末粒径分布的平均值,即30 μm。45#碳钢基体的长度、宽度分别为粒子直径的6 倍及4 倍,较大的基体尺寸可以有效忽略粒子沉积过程中基体边界节点对基体中心变形区域的影响[14]。根据表面粗糙度定义[15-16],设定相邻两波峰或者波谷的水平距离为l,相邻两波峰与波谷的水平位差为波高h。当50 图3 不同表面粗糙度下基体表面形貌Fig.3 Surface morphology of substrate under different surface roughness 考虑到网格尺寸对材料的热传导以及塑性变形会产生很大影响[20],因此对计算区域进行网格细化,以保证计算精度。本模型网格划分过程中,粒子与基体的网格尺寸为0.5 μm。 针对图3 所示的二维有限元模型,对基体的底面施加全约束,对基体侧面施加Non-Reflecting 边界条件,其余表面均设置为自由状态。粒子与基体的接触算法采用2D-Automatic-Single-Surface 接触算法,基体预热温度设置为常温298 K。 WC-12Co 粒子与45#碳钢基体的弹性响应采用线弹性模型,塑性响应采用Johnson-Cook 塑性模型,该模型综合考虑了粒子沉积过程中的应变强化、升温熔化、摩擦以及塑性功与热能之间的转化。粒子与基体的热材料模型选取Thermal-Isotropy-Phase-Change模型。为减少计算误差,计算所用数据均来自实验测量。Johnson-Cook 塑性模型具体表达式[21]如下: τ表示材料屈服应力,εp表示材料等效塑性应变,ε˙p表示材料等效塑性应变率,ε˙0表示材料参考等效塑性应变率,T表示材料温度,Tr表示材料参考温度,Tm表示材料熔化温度(固液相分界线),A表示静态屈服强度,B表示应变强化模量,C表示应变率强化模量,m表示温度软化指数,n表示应变强化指数。表达式第一项 [A+B(εp)n]表示等温状态下,材料应力与应变之间的函数关系;表达式第二项 (1+Clnε˙*)与第三项 [1 -(T*)m]分别表示材料应变率以及材料温度对材料屈服应力的影响。WC-12Co 粒子与45#碳钢基体的材料属性如表1 所示。 表1 粒子与基体参数[5,12]Tab.1 Particle and substrate parameters[5,12] 设定粒子与基体表面的接触位置为基体表面波谷最深处,以最大程度表征波峰与波谷高度差对粒子沉积行为的影响。由于粒子沉积过程绝热,二者的温升均源于二者塑性功的转化与摩擦生热[22]。针对粒子沉积过程中的能量流动,存在如下关系: 式中,EKp为粒子初始动能,UKp为粒子内能变化,UKs为基体内能变化,Up为粒子弹性势能,Us为基体弹性势能,Tp为粒子温升,Ts为基体温升。 图4 为初始速度Vp=500 m/s、初始温度Tp=800 K的球形粒子在不同表面粗糙度的45#碳钢基体上的最终沉积形貌。图4a 为Ra=0 μm 时(理想表面)粒子沉积形貌示意图,粒子扁平化变形均匀明显,但粒子边缘存在明显翘曲,基体中心存在轻微凹陷,变形程度较低,粒子与基体结合面积有限。非理想表面情况下,伴随基体表面粗糙度增加,基体表面的波峰与波谷高度差增加,粒子与基体的结合面积逐渐增大,但是粒子扁平化程度逐渐下降,粒子沉积形貌由Ra=0 μm 时的形状规则对称逐渐向不规则变形转变。此外,同一基体表面粗糙度下,粒子两侧波峰高度的不同,将导致粒子两侧不同程度的塑性变形,观察图4b—d 可得,波峰高度相对较低的一侧的粒子,塑性变形程度较高。当Ra增加至10.26 μm 时,波峰与波谷的高度差相当于粒子直径,粒子水平铺展对两侧波峰造成挤压,并增加波谷深度,粒子变形全过程均在波谷内完成,并对波谷产生填充弥补作用。 图4 不同基体表面粗糙度下的粒子沉积形貌(等效塑性应变)Fig.4 Particle deposition morphology under different substrate surface roughness (equivalent plastic strain) 原因在于粒子沉积过程主要包括粒子垂直压缩与水平铺展两个过程。Ra=0 μm 时,基体表面光滑平整,粒子在各方向受力均匀,且扁平化变形消耗的动能较低,粒子可以实现自由铺展变形且形貌对称[11]。伴随基体表面粗糙度增加,粒子的扁平化将受到波峰的阻碍作用,波峰与波谷的高度差越大,粒子水平铺展所受阻力越大,从而抑制粒子扁平化变形。当Ra增加至10.26 μm 时,波峰与波谷的高度差相当于粒子直径,由于粒子水平铺展挤压两侧波峰,将消耗极大的动能,剩余能量不足以变形,越过波峰,因此粒子的变形过程均在波谷内完成,并在谷底以及波峰侧面堆积。此外,当Ra=10.26 μm 时,粒子沉积至波谷底部与沉积至波峰不同位置处的形貌具有显著差异。 图5 为不同沉积位置处粒子的沉积形貌示意图。图5a 为粒子撞击波峰顶部时的沉积形貌示意图,粒子撞击波峰顶部后,波峰受到粒子挤压下陷,并嵌入粒子内部,此时波峰仅受到垂直压缩力,同时粒子沿波峰两侧向下铺展,并填充波谷,粒子中部的塑性变形明显高于两侧,粒子撞击点附近形变充分,其余部分无明显形变。图5b 为粒子撞击波峰中部时的沉积形貌示意图。粒子撞击波峰中部后,波峰将对粒子产生“切割”作用。粒子左侧部分与波峰产生明显的塑性变形,波峰既垂直压缩嵌入粒子内部,又同时产生水平位移铺展于基体表面;粒子右侧部分沿波峰侧面切向铺展,并对波谷进行填充弥补,但是二者之间的填充仅局限于二者一定程度上的塑性变形,且填充部分存在明显的间隙。 图5 不同沉积位置处粒子沉积形貌示意图Fig.5 Schematic diagram of deposition morphology of particles at different deposition positions: a) crest top; b) middle of the wave crest 粒子撞击波峰顶部时,波峰的塑性变形消耗了粒子大量动能,粒子中部受压产生变形,两侧受惯性影响向下铺展;当粒子撞击波峰中部时,波峰同时受到水平与垂直压缩力,因此产生双向位移,由于右侧部分粒子温度远低于材料熔点,粒子仅产生塑性变形而非粘性流动[23],无法完全沿波峰侧面切向变形,因此二者存在一定间隙。 综上,不同基体表面粗糙度下粒子最终沉积形貌存在明显差异,随基体表面粗糙度增加,粒子与基体结合面积逐渐增大,但粒子扁平化变形程度下降,粒子沉积形貌由Ra=0 μm 时的规则对称形状逐渐向不规则变形转变。粒子沉积过程中,需具备足够动能越过波峰,完成扁平化变形,否则将完全填充弥补波谷。粒子沉积位置不同,将引起粒子最终沉积形貌的不同。不同点在于:沉积至波峰顶部,将引起波峰剧烈压缩变形,并嵌入粒子内部;沉积至波峰中部,将引起波峰垂直压缩与水平铺展,同时对粒子产生“切割”作用,部分位置塑性应变剧烈;沉积至波谷,底部粒子对两侧波峰造成挤压,并增加波谷深度。相同点在于,粒子均会对波谷进行不同程度地填充,并存在一定间隙。 前文描述了不同基体表面粗糙度下粒子沉积变形行为的总体变化趋势,本节将重点探讨基体表面粗糙度对粒子屈服应力的影响。设定粒子初始速度Vp=500 m/s,初始温度Tp=800 K,设定粒子等效塑性应变最大处作为监测点,以进行粒子屈服应力观察。 图6 为不同基体表面粗糙度下粒子屈服应力云图。粒子沉积过程中,粒子中下部的屈服应力均高于粒子顶部,粒子先接触基体的部分的屈服应力高于后接触部分。原因在于沉积过程中,粒子中下部产生剧烈塑性变形,发生加工硬化与应变率强化现象[24],导致屈服应力增加,粒子顶部无形变,因此粒子中下部的屈服应力均高于粒子顶部。同理,粒子先接触基体的部分的塑性应变程度高于后接触部分,加工硬化与应变率强化现象更为严重,因此粒子先接触基体的部分的屈服应力高于后接触部分。 图6 不同基体表面粗糙度下粒子屈服应力云图Fig.6 Distribution of yield stress of particles under different substrate surface roughness 图7 为不同基体表面粗糙度下粒子屈服应力峰值变化曲线。由图可得,理想表面的屈服应力峰值与Ra=5.34 μm 时近似相等,约为2.8 GPa。基体表面粗糙度Ra<10.26 μm 时,粒子的屈服应力峰值变化曲线趋势总体相同,均呈现先升、后降、再震荡。当基体表面粗糙度Ra=0 μm 时,粒子屈服应力最终下降至0。非理想表面状态下,Ra逐渐增加时,粒子的屈服应力稳定变化范围逐渐减小。当Ra=10.26 μm 时,粒子的屈服应力波动剧烈,且出现“二次激增”趋势。 图7 不同基体粗糙度下粒子屈服应力变化曲线Fig.7 Yield stress curve of particles with different substrate surface roughness 粒子沉积过程中,等效塑性变形峰值位于粒子与基体的结合薄壁界面处,当等效塑性变形引起足够温升时,热软化效应相对加工硬化以及应变率硬化占据主要优势,粒子将发生绝热软化现象[25],加之材料热力性质波动以及应变、应变率、温升等因素干扰,绝热软化会转变为绝热剪切局部化,粒子局部区域屈服应力迅速下降为0。Ra=0 μm 时,粒子热软化效应占据主要优势,因此产生上述现象;Ra=10.26 μm 时,波峰与波谷的高度差逐渐接近于粒子直径,粒子的扁平化过程受波峰阻力较大,加工硬化以及应变率硬化相对热软化效应占据主要优势,导致屈服应力峰值逐渐上升;Ra=10.26 μm 时,粒子在沉积过程中产生“一次、二次形变”,“一次形变”发生于粒子与波峰“侧壁”碰撞,侧壁对粒子产生挤压,粒子屈服应力发生突变,“二次形变”发生于粒子与波谷底部接触,粒子挤压波峰的同时,将加深波谷深度,形成沉积坑,粒子自身塑性变形增加,导致屈服应力二次增加。 综上,粒子沉积过程中,粒子中上部与先接触基体部分的屈服应力均高于粒子底部与后接触部分,理想表面的屈服应力峰值与Ra=5.34 μm 时近似相等,约为2.8 GPa。Ra=0 μm 时,因发生“绝热剪切局部化现象”,粒子屈服应力下降至零。Ra一定程度的增加将降低粒子屈服应力,但Ra过大将导致粒子产生二次形变,屈服应力出现“二次激增”现象。 前文描述了不同基体表面粗糙度下粒子屈服应力的变化情况,本节将重点探讨基体表面粗糙度对粒子等效塑性应变的影响。设定粒子初始速度Vp=500 m/s,初始温度Tp=800 K。设定粒子等效塑性应变峰值处作为监测点,以进行粒子等效塑性应变观察。 根据图4 不同基体表面粗糙度下粒子等效塑性应变云图可知,4 种情况下,粒子中下部的等效塑性应变程度均高于粒子顶部,同时粒子中心轴线对称位置处的塑性应变程度亦不相同,粒子先接触基体的部分的等效塑性变形程度高于后接触部分。原因在于粒子中下部与基体表面直接接触产生形变,消耗大量粒子动能,而粒子中上部无法与基体直接接触,因此粒子中下部等效塑性应变程度高于粒子顶部。由于基体表面形貌不均匀,粒子中心轴线对称位置与基体表面波峰接触存在先后顺序,率先与基体表面接触的粒子将消耗大量动能,产生剧烈塑性变形,而后接触的粒子则消耗较少动能,导致变形程度较低。 图8 为不同基体粗糙度下粒子等效塑性应变曲线。由图可得,不同基体表面粗糙度下,粒子的等效塑性应变变化趋势相同,均呈现先升、后平稳的趋势。当基体表面粗糙度Ra=0 μm 时,粒子的等效塑性应变峰值最大为2.03,伴随基体表面粗糙度逐渐增加,粒子的等效塑性应变均低于理想表面情况,Ra=2.51、5.34、10.26 μm 时,对应等效塑性应变峰值分别为1.57、1.83、0.46,呈现出先增后降趋势,且Ra=10.26 μm 时的等效塑性应变明显低于其他情况。 图8 不同基体粗糙度下粒子等效塑性应变变化曲线Fig.8 Equivalent plastic strain curve of particles with different substrate roughness Ra=0 μm 时,基体表面光滑平整,粒子在各方向受力均匀,且扁平化过程消耗动能较低,粒子可以实现自由铺展变形,因而扁平化塑性变形程度较高。伴随基体表面粗糙度逐渐增加,波峰与波谷的高度差逐渐接近于粒子直径,粒子的扁平化过程受波峰阻力影响,逐渐增大,波峰与波谷的存在将抑制粒子水平铺展,降低粒子塑性变形程度,因此粒子的等效塑性应变均低于理想表面情况。Ra=5.34 μm 时,粒子两侧碰撞基体的时间差较大,先接触基体一侧的粒子消耗大量动能,塑性变形程度剧烈,且只有单侧粒子跨越波峰进行水平铺展。而Ra=2.51 μm 时,粒子两侧几乎同时与基体表面接触,且两侧都越过波峰进行水平铺展,因此等效塑性变形程度相对Ra=5.34 μm 有所下降。Ra=10.26 μm 时,波峰与波谷的高度差超越粒子直径,粒子沉积过程中,粒子挤压两侧波峰形成波峰偏移,消耗大量粒子动能,同时波谷深度增加,粒子整体镶嵌于波峰之间,因此自身塑性变形程度较低。 综上,粒子沉积过程中,粒子中下部的等效塑性应变程度高于粒子顶部,同时粒子中心轴线对称位置处的塑性应变程度亦不相同,粒子先接触基体的部分的等效塑性变形程度高于后接触部分。Ra=0 μm 时,粒子等效塑性程度最大,等于2.03。非理想平面状态下,一定程度增加Ra时,波峰波谷的存在可促进粒子等效塑性变形,但是过度增加Ra将引起波峰变形偏移,导致粒子能量消耗殆尽,粒子等效塑性变形程度下降。 前文描述了不同基体表面粗糙度下粒子的等效塑性应变变化情况,本节将重点探讨基体表面粗糙度对粒子温度的影响。设定粒子初始速度Vp=500 m/s,初始温度Tp=800 K,设定粒子等效塑性应变最大处作为监测点,以进行粒子温度观察。 图9 为不同基体粗糙度下粒子温度云图,由于粒子温升均源自粒子自身等效塑性变形,因此粒子的温度分布与等效塑性应变分布相同。4 种情况下,粒子中下部的温升幅度均高于粒子顶部,同时粒子中心轴线对称位置处的温升幅度亦不相同,先接触基体的粒子部分的温升幅度高于后接触部分。 图9 不同基体粗糙度下粒子温度云图Fig.9 Distribution of temperature of particles under different substrate surface roughness 粒子中下部与基体表面直接接触产生形变,消耗大量粒子动能,而粒子顶部无法与基体直接接触,因此粒子中下部等效塑性应变程度高于粒子顶部,从而粒子中下部的温升幅度高于粒子顶部。由于基体表面形貌不均匀,粒子中心轴线对称位置与基体接触存在先后顺序,率先与基体接触的粒子部分将消耗大量动能,产生剧烈塑性变形,而后接触的粒子部分则变形程度较低,因此先接触基体的粒子部分的温升幅度高于后接触部分。 图10 为不同基体粗糙度下粒子温度峰值变化曲线。由图可得,4 种基体表面粗糙度下,粒子的温升峰值变化趋势相同。Ra=0 μm 时,粒子温升峰值最高,为1562 K;Ra= 2.51、5.34、10.26 μm 时,相应温升峰值表现为先升后降的趋势,分别为1455、1496、1075 K。Ra=0 μm 与5.34 时,粒子温升峰值幅度十分接近,二者温差仅66 K。原因在于,粒子沉积过程中,粒子的温升主要源于自身的等效塑性应变,粒子与基体之间的摩擦可引起部分温升,但是相对等效塑性应变而言,对粒子的温升峰值影响较小,粒子温升峰值变化趋势与粒子等效塑性应变变化趋势总体一致。 图10 不同基体粗糙度下粒子温度峰值变化曲线Fig.10 Temperature curve of particles with different substrate roughness 综上,粒子沉积过程中,粒子的温升源于自身等效塑性应变与摩擦生热,粒子中下部的温升幅度高于粒子顶部,同时粒子中心轴线对称位置处的温升幅度亦不相同,先接触基体的粒子部分的温升幅度高于后接触部分。Ra=0 μm 时,粒子温度峰值最高为1562 K;Ra=0、5.34 μm 时,粒子温升幅度十分接近,二者温差仅为66 K。 本文采用线弹性本构模型以及Johnson-Cook 塑性模型,开展了基体表面粗糙度对WC-12Co 粒子在45#碳钢基体上的沉积行为的影响分析,结论如下: 1)不同基体表面粗糙度下粒子最终沉积形貌存在明显差异。Ra=0 μm 时粒子沉积形貌对称但粒子-基体结合面积最小。伴随基体表面粗糙度增加,粒子沉积形貌逐渐向不规则变形转变,且粒子与基体结合面积逐渐增大。粒子沉积过程中,粒子动能充足对于翻越波峰,完成扁平化变形至关重要,否则粒子将填充弥补波谷;粒子沉积位置对粒子最终沉积形貌影响甚重,沉积至波峰顶部将引起波峰压缩变形,并嵌入粒子内部,沉积至波峰中部将引起波峰垂直压缩与水平铺展,同时对粒子产生“切割”作用,沉积至波谷底部将对两侧波峰造成挤压,并增加波谷深度。相同点在于粒子均会对波谷进行不同程度的填充,并存在一定间隙。 2)粒子沉积过程中,受热软化、加工硬化以及应变率硬化效应综合影响,粒子屈服应力与等效塑性应变变化趋势接近一致,粒子中下部与先接触基体处均高于粒子顶部与后接触部分。Ra=0 μm 时,粒子等效塑性程度最大,等于2.03,但粒子屈服应力因热软化效应相对加工硬化以及应变率硬化占据主要优势最终下降至零。非理想表面状态下,一定程度增加Ra可促进粒子等效塑性变形,降低粒子屈服应力,但Ra过大将导致粒子等效塑性变形程度下降,屈服应力出现“二次激增”趋势。 3)粒子沉积过程中,粒子温升与等效塑性应变变化趋势总体一致,粒子中下部与先接触基体处的温升程度均高于粒子顶部与后接触部分;Ra=0 μm 时,粒子温度峰值最高为1562 K,Ra=0 与5.34 μm 时,粒子温升幅度十分接近,二者温差仅为66 K。 4)综合比较,Ra=5.34 μm 时,粒子屈服应力、等效塑性变形程度、温升幅度在非理想表面状态下最佳,粒子与基体结合状态最优。因此,一定程度提升基体表面粗糙度有助于改进粒子与基体之间的结合状态,提升涂层性能,但过度提升基体表面粗糙度将抑制粒子变形,导致粒子-基体间存在间隙,增大涂层孔隙率,导致涂层性能下降。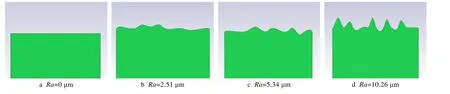

1.2 材料模型
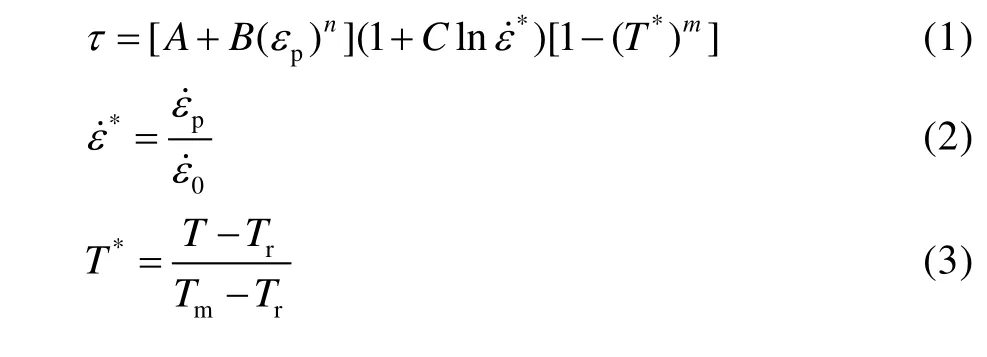
2 结果与讨论
2.1 喷涂粒子沉积动态变形行为


2.2 基体表面粗糙度对粒子屈服应力的影响
2.3 基体表面粗糙度对粒子等效塑性应变的影响

2.4 基体表面粗糙度对粒子温度的影响

3 结论
