基于最小二乘配置的预行程误差模型*
2021-08-02汤泽航张揽宇
汤泽航,高 健,张揽宇
(广东工业大学省部共建精密电子制造技术与装备国家重点实验室,广州 510006)
0 引言
在线检测(OMM)系统通过在数控机床上安装一个接触式或非接触式探头,实现在加工过程中或加工后实时检测零件质量,而不需要重新装夹,从而避免了二次装夹带来的严重误差[1-3]。这种方法能够显著提高自由曲面零件诸如航空航天薄壁类零件的加工精度和加工效率[4-5]。触发式探针是最常用的OMM系统工具,然而其在触测过程中存在的预行程误差是影响在线检测测量误差的一个重要因素[6-7]。文献[8]通过实验得到预行程误差占在线检测测量总误差的60%。因此,分析研究触测头检测过程中的预行程误差,建立相应的误差模型以及预测补偿模型,对提高在线检测系统的检测精度具有相当重要的意义。
目前,在线检测系统研究领域,一些学者专门针对预行程误差的补偿问题进行了研究。文献[9-11]对接触式探针结构进行了分析,归纳出测杆长度,触测速度,触测方向等对预行程误差的影响,为进一步的补偿工作提供了理论基础。但实际上,探针预行程误差的影响因素较多且复杂,用其方法只能在一定程度上估算预行程误差,补偿效果有所欠缺。鉴于预行程误差分布模型的非线性,传统的理论推导方法无法得到精度较高的误差模型,文献[12-14]通过探测得到标准球上部分点的预行程误差作为训练数据来建立BP神经网络模型,从而预测出其他点的预行程误差。针对BP神经网络易形成局部极小且训练次数多、收敛速度慢等缺陷,文献[15]提出了基于正则化RBF神经网络模型,并取得了较高的预测精度。但是,神经网络模型的预测精度一般需要大量的训练数据和较多的训练次数来保证,在某些场景下的应用会受到限制。
鉴于以上在线检测预行程误差建模方法的不足,为了建立一个高精度、高稳定性的预行程误差预测模型,本文提出了一种基于最小二乘配置法的误差预测模型,并通过实验与RBF神经网络模型进行对比分析,来验证该方法对于预行程误差的补偿更加精确有效。
1 触发式探针预行程误差实验原理
本文通过合理规划标准球上的探测点并进行所有点的探测,从而为建立预行程误差预测模型提供了数据基础。在用接触式探针做检测时,由于触测力的存在,在触球接触被测物体时,探针并不会立即触发测量信号,而是继续沿检测方向上行进一小段距离[16-17],这个过程中测杆也产生一定的力学形变。因这一小段距离导致的测量误差,被称为预行程误差。测杆的长度、刚度以及测头内部触发结构等原因都会对预行程误差产生影响。本文中实验采用的接触式探针为触发式无线测头系统ACC-CP52,测球直径为φ6 mm。
将标准球上的检测点用极坐标(ρ,φ,θ)表示,其中ρ表示标准球半径;φ表示纬度角;θ表示经度角。在实验过程中,对同一个陶瓷标准球(直径25.001 1 mm)进行检测,半径ρ不变,因此检测时只考虑球上的经纬度坐标(φ,θ)。
在测量过程中探针是沿着球上测点的理论法矢方向d进行触测的,探针红宝石触球与工件之间可能发生相对滑动。文献[18]研究表明,当触发力与接触工件表面的法线方向夹角小于10°时,探针与工件表面的相对滑动由于摩擦力存在不会发生。极端情况下当夹角大于10°时,会发生相对滑动,但研究表明其相对滑动距离小于1 μm,远小于实际的预行程误差。因此,可以忽略探头与工件表面之间因相对滑动产生的误差。
本文实验将标准球每隔经纬度5°进行网格划分,共生成1297个探测点,如图1所示。用触发式无线探针对所有探测点进行检测得到实际值rreal并与对应的标准球和探针触球半径之和的理论值rideal进行比较,即可得出相应的预行程误差wi,如图2所示。

图1 标准球上探测点分布
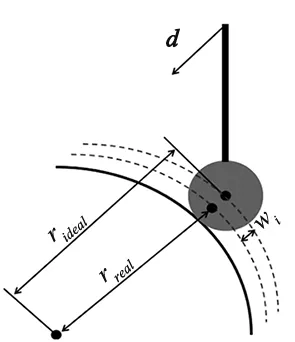
图2 预行程误差形成过程
2 预行程误差预测模型
2.1 经典曲面拟合法
经典全参数曲面拟合模型通过建立预行程误差L与经纬度坐标(φ,θ)的关系式:
L=F(φ,θ)+ξ
(1)
式中,F(φ,θ)为预行程误差L的趋势曲面,ξ为残差。
设
F(φ,θ)=a0+a1φ+a2θ+a3φθ+
a4φ2+a5θ2+a6φθ2+a7θφ2+a8φ3+a9θ3+…
(2)
若测得n个预行程误差数据点,则可得以下矩阵形式:
L=AX+ξ
(3)
式中,
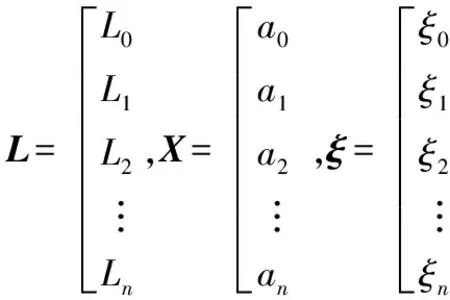
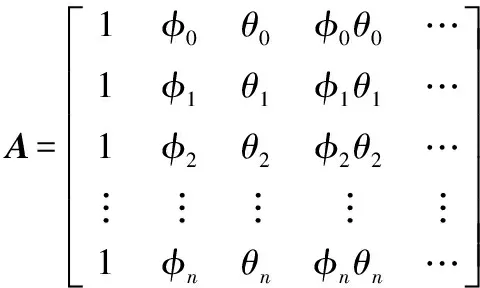
当上式符合最小二乘原则,即残差|ξ2|=min的条件时,求得向量X的解,回代到式(2)中,就可推估出未知方位点的预行程误差值。
在式(2)中,若未知数取n次项,便得到n次多项式曲面拟合。其中拟合次数不宜过大,过大容易造成方程式解不稳定,且易出现过拟合现象,一般取2次即可[19-20]。
2.2 基于最小二乘配置法的预测模型
随着测量技术的发展和检测要求的提高,经典的全参数数据处理方法有时不能满足精度的要求,特别是当检测数据中包含不可消除的较复杂系统误差时[21-22]。因此,综合考虑固定参数效应和随机效应的最小二乘配置模型在测量领域越来越受到关注,它可以说是具备了曲面拟合法和神经网络算法两者的优点。当模型选择正确时,最小二乘残差具有偶然误差的特征,此时得到的拟合模型是最优的。
最小二乘配置的数学模型是[23-24]:
L=AX+BY+Δ
(4)

(5)

(6)
式中,L为n维观测向量;Δ为随机噪声,Δ~N(0,DΔ);X为t维非随机参数;A为n×t阶设计矩阵;Y为随机参数向量,包含n维已测点信号S和g维未测信号S′。In是n阶单位阵,根据矩阵B的构成,可知观测方程中不含未测点信号S′。
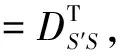
式(4)对应的误差方程为:
V=AX+BY-L
(7)
根据最小二乘原理有:
(8)
式(7)、式(8)中,V是观测值L的改正数;VY是Y的先验期望E(Y)的改正数,从而可以推出:
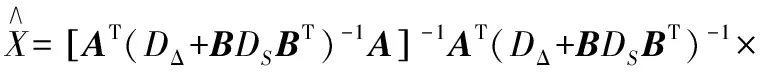
(9)
(10)
(11)
由假设B=I(单位阵),μS=0,μS′=0并且不考虑随机噪声误差的影响,即DΔ=0,则式(9)、式(10)、式(11)可表示为:
(12)
(13)
(14)
从而得到未测点的平差值,即未知点的预行程误差:
(15)
上述最小二乘配置模型的计算过程中求解的关键是信号Y与Y之间的协方差。现阶段各种类型的协方差函数均为与空间距离相关的某种函数,考虑预行程误差的空间相关性,本文采用空间平方根函数作为信号间的协方差函数模型,亦即:
(16)
式中,(xi,yi,zi),(xj,yj,zj)为球面检测点的坐标;Dij为i,j两点的随机参数(信号)Si与Sj间的协方差。
根据上述最小二乘配置法原理,针对预行程误差实验模型,从分布于标准球面的144个探测点的预行程误差中选取72个数据点作为已知点建立预行程误差模型,剩下的72个探测点数据作为预测模型的验证数据。建立模型后输入需要预测点的纬度和经度方位信息(φ,θ),则输出该探测点的预行程误差预测值。
3 实验分析
选取分布于标准球面的72个数据点作为已知点建立预行程误差模型,其余72个点作为检核点,采用RBF神经网络算法和本文提出的基于最小二乘配置模型2种算法做了预行程误差的预测结果比较实验。
将预测结果与相应的实际预行程误差数据做对比,从而得到RBF神经网络模型与基于最小二乘配置法的预行程误差预测模型的预测精度。其预测结果如图3、图4所示,实线曲线代表实际测得的预行程误差,虚线曲线分别代表RBF神经网络模型和基于最小二乘配置法的预测模型得到的预测数据。两条曲线的重合程度反映算法的预测精度。由图3、图4可以看出,基于RBF神经网络模型其预测结果与实际数据已经非常接近,也能够反映预行程误差的随机性;而基于最小二乘配置法的预测模型在具有以上优点的基础上做到了精度更高,误差波动更小,其预测结果与实际数据基本重合,无明显差距。
由图5、图6预测误差图可看出,基于RBF神经网络的预测模型其大部分预测点残差在4 μm左右,其中最大预测误差为10.85 μm,个别点的预测误差在6~8 μm左右,平均误差为2.587 9 μm,残差标准差为2.332 7 μm。而基于最小二乘配置法的预测模型大部分预测点的精度都在2 μm以下,个别点的预测误差在4 μm左右,且只有一个点的预测误差在7 μm左右。由于预行程误差在空间中的分布是相互关联的,且相距较近的对象之间影响力远大于较远的,因此采用空间平方根函数作为先验协方差的最小二乘配置模型其总体预测误差更小。由图中还可以看出预测点误差波动较大,这与机床在反向运动时的方向间隙有关。与RBF神经网络模型相比,本文基于最小二乘配置法的预测模型其精度统计结果如表1所示。采用最小二乘配置预测模型的预测误差平均值为1.395 0 μm,其标准差为1.426 3 μm。平均预测精度相比RBF神经网络模型提高了38.86%,预测结果更加稳定可靠。
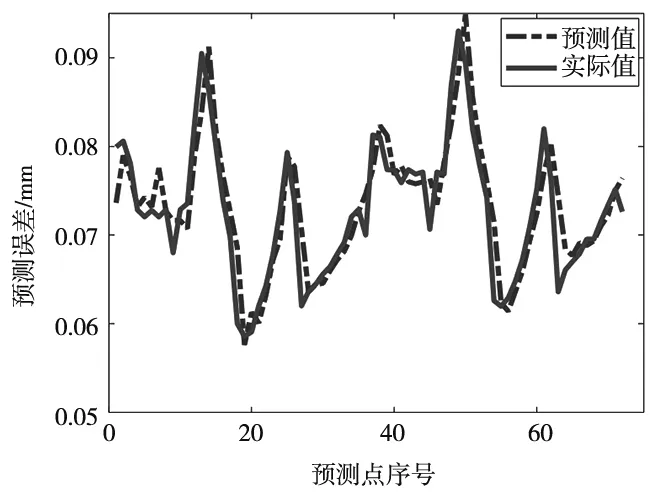
图3 神经网络模型预测值与实际值对比
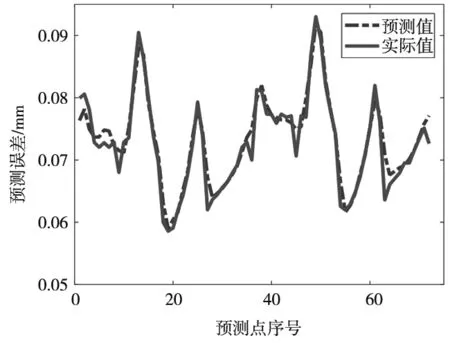
图4 最小二乘配置模型预测值与实际值对比
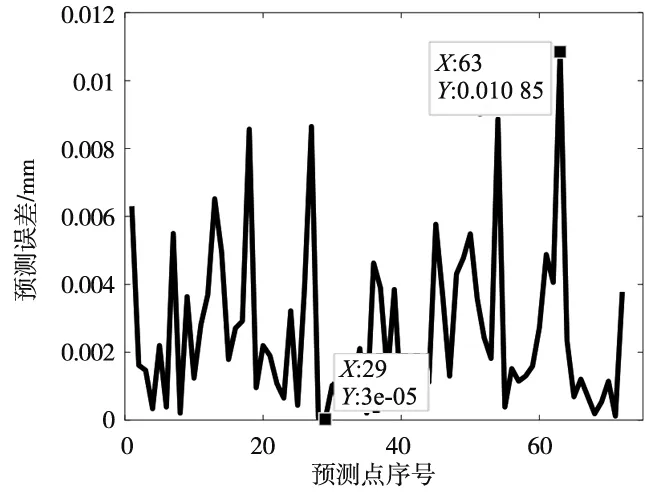
图5 神经网络算法模型预测误差
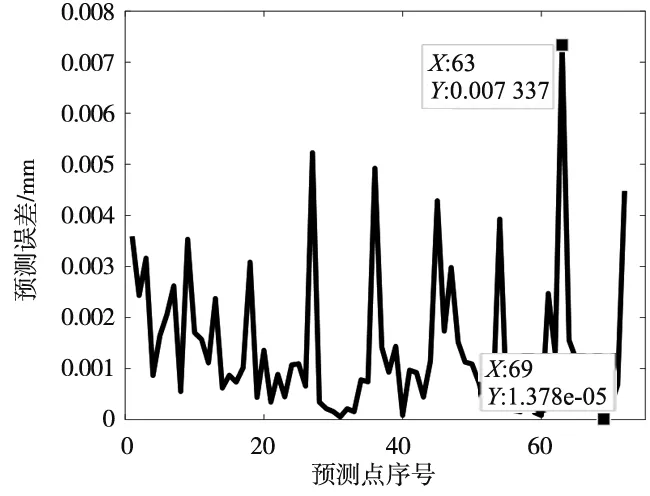
图6 最小二乘配置模型预测误差
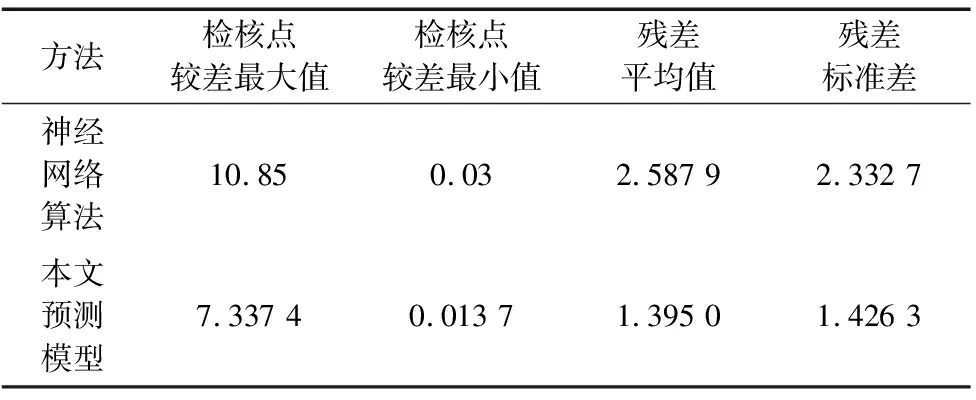
表1 预测精度统计表(μm)
4 结论
本文针对OMM系统的预行程误差补偿问题,提出了一种基于最小二乘配置法的误差预测模型。通过采用空间平方根函数作为先验协方差,确保了该模型的预测结果能够综合考虑到预行程误差的空间相关性。同时设计了与RBF神经网络模型的对比实验,证明了本文方法对预行程误差预测结果的有效性和准确性。通过实验结果可知,基于最小二乘配置法的预测模型适用于非线性且具有一定空间相关性的对象,能够提高预测结果的精度和可靠性。该方法也可应用于CMM(三坐标机)的测量系统误差补偿, 将在今后的工作中做进一步的研究。
