基于DT和SVM分类器的中文文本情感极性分析

宋尚文，卢 超，阎红灿

（华北理工大学理学院，河北 唐山 063210）

0 引言

随着深度学习领域的发展，自然语言处理问题的解决方式也逐渐向深度学习偏移[1]。情感分析是自然语言处理中常见的场景，比如说电商、餐饮、娱乐等等产品的使用用户评价信息，对于指导产品更新迭代都具有关键性作用。

由于中英文语系的差异较大，英文的情感分析主要问题在于词性标注、词汇粒度、句法结构、词汇之间的关联关系等；中文特点很明显，在自然语言处理的过程中第一步是分词，而英文天然情况下就是存在空格的，中文分词就是一个很有挑战性的任务，除此之外，由于中华文化发展源远流长，汉字之间的关联性、省略内容填充和内容补足等方面来说都是难以进行处理的。

因此国内外在中文的情感极性分析相对于英文或者其它语言来说有更多对应的深度学习方法。如今中文的自然语言处理领域已进入了深度学习时代，大部分方法将词作为底层特征，在此特征基础上，完成了词性标注、命名实体识别和语义角色标注等多个任务，之后利用递归神经网络完成了句法分析、情感分析和句子表示等多个任务，这也为语言表示提供了新的思路。

从数据集角度分析，新闻类的数据客观性极强，较为朴素的传统机器学习方法有可能在处理其问题时保证一定的正确率的同时会具有更加突出的效率。本文选用DT（Decision Tree，决策树）和SVM（support vector machine，支持向量机）两大类分类器应用于情感极性分析中进行研究。

1 模型选择

1.1 多分类的支持向量机

SVM起初是针对二分类问题提出的，但是实际应用中多分类问题更加普遍。它的核函数的利用使它成为实质上的非线性分类器，SVM基本思路是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。非线性分类时相对应的在高维空间使用 SVM 求解分类问题则需要更换核函数，其意义是利用核函数计算目标函数而去代替最原始的内积计算。

并且支持向量机[2]的优点就是很适合小数量样本数据，解决高维的问题，由于求解的是几何间隔最大的分离超平面因此可解释较强。

针对现有数据集，选择SVM是一个合适的选择。核函数不是 SVM 专属的，但是它的优化方向会涉及到各种场景，多分类，类别不平衡都可以通过改变核函数来适应场景。为避免分类训练时间过长与过度拟合和较大程度适应高维空间的分类，引入两类核函数：（1）linear核函数的特点是参数少速度快，对于一般的数据分类效果比较理想；（2）rbf核函数的特点就是将可数据映射至高维空间解决复杂且抽象的分类任务。本文采用rbf和linear两种基础核函数加入训练与对比分析。

1.2 决策树分类

决策树是一种逻辑简单的机器学习算法，采用树形结构，需要监督学习。在样本集合中针对每个样本都有一组属性和一个分类结果，通过样本的学习的得到一个决策树，再对测试集数据给出正确的分类。决策树由图1所示三种元素构成，根节点：包含样本的全集；内部节点：对应特征属性测试；叶节点：代表决策的结果 DT中有几种典型的方法ID3、C4.5和CART（Classfication And Regression Tree，分类与回归树）等。CART的分类效果一般优于其他决策树，其是一个二叉树，也是一个回归树，同时也是分类树。相对与ID3和C4.5，CART的优势[3]在于在分类过程中只能将父节点分为两个子节点，采用基尼指数决定是否进行节点的分裂。与熵的概念类似，数据内部的类别越繁杂基尼指数就会越大。作为回归树，CART对叶子节点内部的数据进行均值方差计算，以此来换取计算成本，过程中存在细小分割，但是其支持剪枝，可以有效地避免过度拟合的问题。

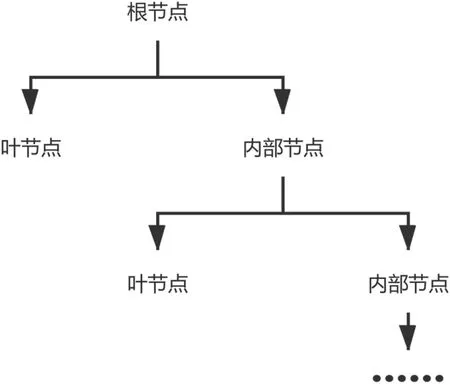
图1 决策树的树形结构Fig.1 The tree structure of the decision tree

结合上述的分析，本文实验中在选取 CART作为决策树方法的分类器。

2 数据处理

2.1 数据文件处理及数据分析

数据集提供三个文件（训练集、训练集标签、测试集）为常规的数据科学竞赛提供的数据种类，本文则使用训练集与训练集标签来检验传统机器学习方法的性能。首先需要对训练数据集的文本长度分布，文本标签分布简要进行统计。

图2所示发现新闻字段的长度分布趋势相对稳定的分布在1～6 000位字符的范围，呈现出正偏态分布，其中位数在分布于 3 000左右；图3新闻标签的分布没有体现出平均化，特别是0值（情感极性类别为正面情绪）所占整体数据的比例只有10.47%，显然这属于非均衡的数据集，在构建模型的时候需要考虑到数据不均等[4]的因素。

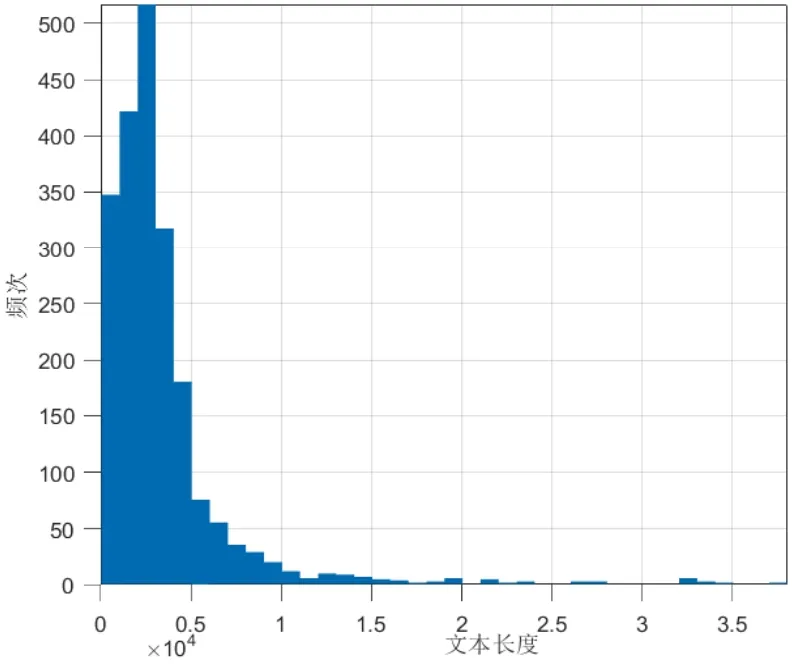
图2 新闻字数统计图Fig.2 News word count statistics

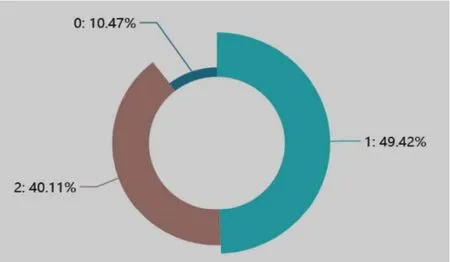
图3 新闻标签统计Fig.3 New s label statistics

2.2 数据预处理及中文分词

数据集中新闻文本资料大多来自互联网，通过简要观察数据可以发现有以下三个问题：（1）训练集数据与标签的序号没有正确的存在对等关系；（2）训练集文本数据分为标题和内容两部分；（3）训练集数据中网络新闻有少量网址信息、手机号码、乱码符号等干扰情感分析的噪声信息。

考虑到训练集数据的问题做如下处理：（1）对数训练集的两个文件进行序号的离散化处理，之后再建立一一映射关系，删除无映射关系的信息，保证训练集数据和标签划分的正确性；（2）新闻文本标题囊括了内容里的主要部分类似于论文的摘要，因此这部分在处理时需要额外保留标题的信息，以后续调整两者拼接比例方式实现（3）为了优化分类效果需要删除其中的所有非中文符号（包含上述第二个问题中的噪声信息与标点符号），之后对相关文本数据进行拼合。利用正则表达式处理数据集的字符串得到完全由中文组成的训练集和测试集两个列表数据。

正则化处理过程主要利用的是 Python的 re库进行操作，其处理函数如下：

英文的行文中单词之间是以空格为分界符，不同于拉丁语系，中文只有字、句、段能通过明显的分界符划分界限，但是在词的这一点没有明显意义上的分界符。中文分词是中文文本处理的一个基本步骤，在中文自然语言处理时进行的预处理通常是要先分词[5]，分词将直接影响词性，句法树等模块的效果。

中文分词技术已经渐渐成熟，根据实现原理主要分为两类，第一类为基于词典的分词算法，一般是按照一定的匹配算法依托一个建立好的充分大的词典进行词语匹配；第二类是基于统计的机器学习算法，常见的分词器都是使用机器学习算法和词典相结合，一方面能够提高分词准确率，另一方面能够改善领域适应性。具有代表性的方法是jieba分词[6]，内部动态规划实现查找最大概率路径，未记录的词语会采用基于汉字成词能力的HMM模型，国内外的高校与公司也开源了分词代码或者分词调用接口，结合分词过程中的代码复杂性、实现的分词程度、调用便捷程度和运算时间复杂度最终选择jieba分词，分词函数代码：

如图4中是数据集使用jieba分词的分词效果。

图4 分词效果Fig.4 Result of word segmenting

2.3 词向量化与句向量化

自然语言处理的分析首先要解决词向量的数字化表达问题，词向量是通过一个高维向量去表达一个词或字。在统计语言模型研究的背景下，Google公司在 2013年开放了一款用于训练词向量的软件（Word2vec）工具[7]。

Word2vec依赖 skip-grams或连续词袋（CBOW）使用一个浅层的神经网络，用一个只具有一个隐藏层的神经网络学习词嵌入，该模型在预测上下文的同时产生了一个副产品，即分词在n维向量空间的表示。简单的理解方法是两个词语的相似程度可以由计算两个高维词向量的余弦得出，余弦函数在实数数域内有上下限，因此可以由余弦的数值来区分两词语的相似度。

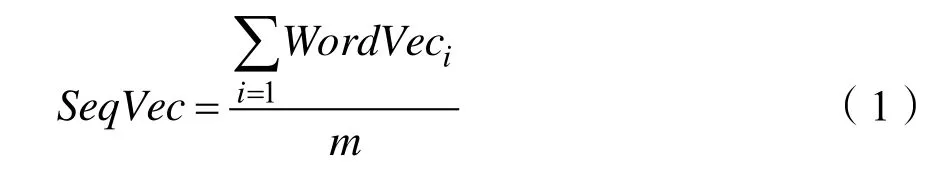
本文采用的句向量计算是无监督学习的词向量的词袋模型。其中最朴素的方法是式（1）所示的预训练词向量求平均的计算方法，其中SeqVec表示句向量，m表示为每个样本中词的个数，分子表达的是词的词向量。 好处是计算速度快，但是缺点忽略了句子的次序，在语句顺序较敏感的中文文本处理问题中效果不佳。针对于新闻的文本信息分析，从其客观确切、简练朴实的角度分析，最终认为线性加权的方法计算句向量在本文数据集中是一种较为客观的方式。

2.4 数据增强

数据增强（Data Aug mentation）是一种通过有限数据产生更多的等价数据来人工扩展数据集的技术。计算机视觉领域中，数据增强的应用更为广泛，通过图片的移动翻转裁剪等手段都可以满足；相反在自然语言处理过程中，数据增强应用更少，其使用在原数据集中进行同义词的更换，随机插入删除等等方法，本文此处将对句向量进行增强，有效避免了二次处理中文语句数据集，不能保证是有利的但是这也同时意味着更大的机遇。

针对不均衡问题，一般有采样和代价敏感学习两种策略，采样的话又分为 over-sampling和under-sampling。其中，smote算法算是 oversampling中比较常用的一种。由于训练集数据的标签不均衡，考虑到训练集与测试集的比例为1∶1。采用过采样是一种比较合理的方法，通过增加分类中样本较少的类别的采集数量来实现平衡。

SMOTE[8-9]的思想是合成新的少数类样本合成策略是对每一个样本a，从它最近邻选一个样本b，然后在a、b之间的连线上随机选取一点作为新合成的少数类样本。算法流程如下：

对于一个样本xi使用K近邻法[10]，定义距离为样本之间的n维特征空间的欧氏距离，以定义方法计算求出距离xi到少数类样本集的所有样本的距离，得到其K近邻；

根据样本不平衡比例设置一个采样比例以确定采样倍率N，对于每一个少数类样本x，从其k近邻中随机选择若干个样本，假设选择的近邻为xn；

对于每一个随机选出的近邻xn，分别与原样本按照上述的公式构建新的样本，其中δ∊ ( 0,1)。

SMOTE 方法生成的样本均分布在xi和xˆi相连的直线上，经过 SMOTE的数据过采样补充形成了10 770×200的训练集句向量，上述描述代码如下：

届时得到的句向量为数据集的常规句向量，为了提升标题在内容中的比重需要进行式（3）的操作，其中λ∊ ( 0,1)，生成句向量的过程比较耗时并且某些标题的长度可能过短，所以不适合进行标题与内容句向量的分别计算叠加。同等意义，本文将随机变量设置使得为整数，之后在进行词向量处理时将标题词向量叠加同等倍数最后合并计算新的句向量即为所要求出的向量结果。

2.5 评价指标的选择

准确率（Accuracy），精确率（Precision）和召回率（Recall）是信息检索，人工智能，和搜索引擎的设计中很重要的几个概念和指标。

其中β是参数，P是精确率，R是召回率，当参数β=1时，理论上解释为精准率与召回率同等重要，这也是数据科学比赛中最常见的排名评价指标。考虑到本文结果应与网络上结果作比较，所以选择 F1-score作为模型的评价指标。

3 两种分类器的应用研究结论

3.1 运行及验证模型

将原始词向量训练集做如下处理：（1）词向量以标题和内容做划分叠加词向量并将标题的特征放大形成最终的句向量；（2）用 SMOTE方法处理句向量数据集使得训练集标签达到相对均衡；（3）将最终形成的训练集抽取20%作为测试集以评估本文使用的方法的性能；（4）使用最原始的词向量生成方式和特征放大经过过采样的数据进行三种方法的训练。

本文训练所使用的计算机环境为：

操作系统：win10 x64

处理器：Intel(R) Core(TM) i5-8250U CPU @1.60 GHz 1.80 GHz

RAM：12 GB

语言环境：gcc version 8.2.0；python 3.7.5

采用F1值作为模型评价指标。由于训练数据量较少得分评估不稳定，结合程序时间复杂度接近O(n2)，所以采取运行20次取均值的方法，得到的多组训练结果如图5所示。

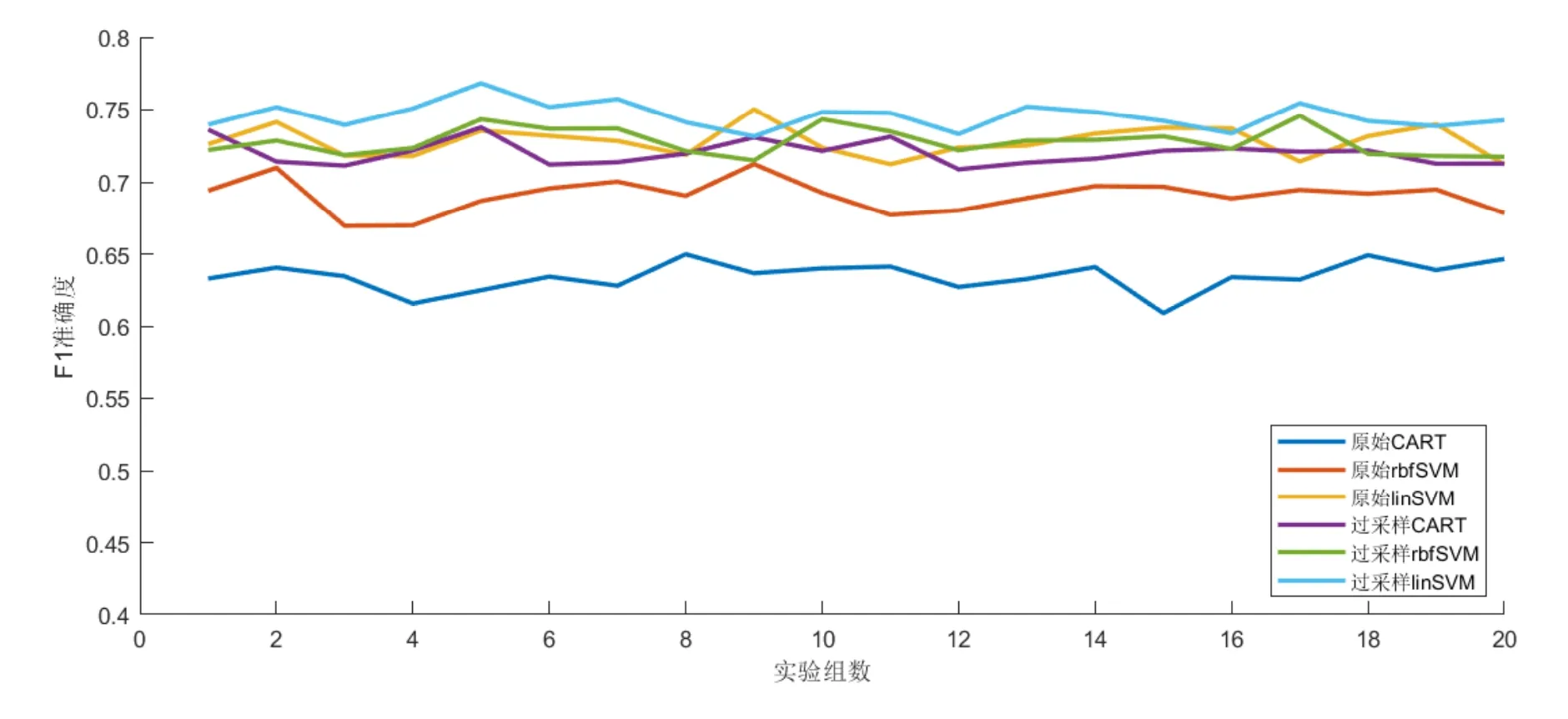
图5 不同训练集与模型的多组学习效果Fig.5 Learning effects of different training sets and models in multiple groups

3.2 结果分析

由运行结果的图像初步分析得出原始 CART和原始 rbfSVM的效果普遍偏低，过采样数据集的测试准确度水平较为均衡，因此得出结论：使用 SMOTE和特征放大的方式可以有效的处理数据不均衡问题并且较不使用其方法的同等试验下能得到较好的结果。

运行20次之后纵向分析，删除数据最大最小值后取均值得表1数据属性，过采样句向量数据的效果均好于同等状态下原始不均衡数据的效果，再次说明数据增强的方法可能适用于在实验中期处理具有一定数学关系的数据；支持向量机方法的处理结果优于决策树方法，并且线性核函数的支持向量机效果相对明显，结合数据量和数据复杂度分析，验证了线性核函数适用于小型数据集、高维特征的多分类问题。

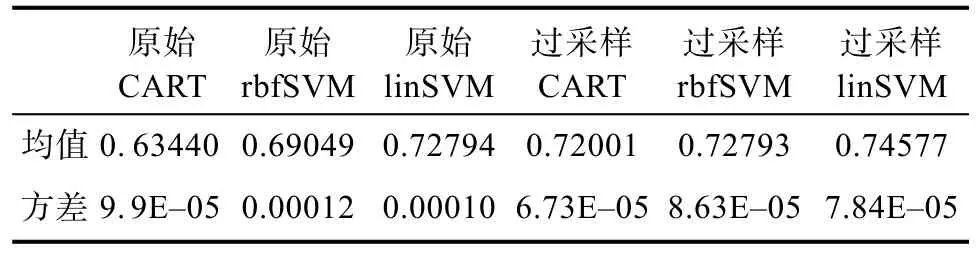
表1 模型训练得分情况Tab.1 M odel training scores

过采样数据条件下采用线性核函数的支持向量机在数据分析中获得评分的均值最高，评分达到 0.74577，且方差为 7 .84× 1 0-5，表示该方法的运行结果相对较平稳。方差角度分析本次实验：六类实验的方差都比较低，实验结果都比较稳定，可信度较高。

4 结论

由实验验证结果与网络数据比赛结果对比可知，利用上述挑选出的最优方法针对互联网新闻情绪极性分析效果较逊色于近几年新产生的中文文本处理方法[11]，尤其是深度学习领域发展的几大类方法重新定义了这类问题。但是从时间效率讲目前来说传统的机器学习方法占用的计算时间损耗和精力要远远小于深度神经网络方法，从框架的使用难度、神经网络的原理角度来看，深度学习的复杂程度较高，在未来的机器学习中，深度学习会占据绝大部分领域。但是在小型且特征明显的数据处理时，采取本文使用的线性核函数的支持向量机方法也会得到准确率与深度学习方法相当的结果。

利用新颖的自然语言处理文字处理方法结合传统的数据挖掘中常用的分类训练方法可以基本解决语义较清晰的中文文本情绪分类任务，但是在很多方面还有进步空间比方说：数据维度处理过大而采用了普通的计算方式，运算效率相对较低；词向量到句向量的处理过于朴素在一定程度上可能丢失了有价值的信息从而影响了准确率等等。