一种高效的概率图上Top-K极大团枚举算法

王 恒，周军锋，杜 明

(东华大学，上海 201620)

0 引言

图是一种由顶点和边组成的常见数据结构，图中的顶点可以用来表示不同的实体，边可以用来表示两个实体之间存在着联系。现实生活中，图被广泛应用于解决各种各样的问题，比如旅行商问题[1]、运输问题[2]、网络流问题[3]、复杂网络系统[4-6]等。对于图中的任意顶点集，如果该集合内任意两个顶点之间都存在边，那么称该点集为团。如果该团不被任何其他的团所包含，则称这个团为极大团。在概率图中，如果一个极大团的团概率大于等于阈值α，那么称该团是α-极大团。

极大团的枚举是图模型上的一个基本研究[7-10]。然而，真实的图规模很大，枚举所有的极大团非常耗时，并且很多小规模的团能够提供的信息很少，没有枚举的价值。在此基础上，有学者提出了Top-K极大团枚举问题，即枚举图中规模最大的K个极大团，现有的Top-K极大团枚举算法多半是基于确定图的。

实际研究中，确定图的Top-K极大团枚举并不能解决实际数据由于噪声所产生的不完整、不精确的问题。所以，将Top-K极大团枚举放在概率图上研究更具有实际意义[11-12]。现有的算法在概率图上求解Top-K极大团时，返回的是团概率最大的前K个团。由于极大团的团概率会随着顶点规模的变大而不断减小，这种枚举方式会丢掉很多规模大而概率较小的极大团，这些大规模极大团往往包含很多信息，有重要的研究价值。针对以上研究存在的不足，本文重新定义了概率图上的Top-K极大团枚举问题，即返回团概率大于阈值的前K个顶点规模最大的极大团。在此基础上提出了一种在概率图上枚举Top-K极大团的算法Top-KC。此外，本文对该算法提出了两种优化方法，两种优化分别依据顶点的度和Core-Number对顶点重新排序，依据新的顶点顺序枚举α-极大团，并在枚举过程中利用剪枝策略减少不必要的计算。实验结果表明，本文提出的优化策略可以有效提高枚举极大团的效率。

1 相关工作

1.1 问题定义

给定概率图G = ( V,E,β)，其中 V代表所有顶点的集合，E代表所有边的集合，β代表每一条边上概率的集合，|V|代表图G的顶点个数，|E|代表图 G的边数。表1给出了文中相关符号的解释。

表1 符号说明Tab.1 Sy mbol description

定义1 团在给定图G=(V,E)中，如果存在一个点集V'⊆V，并且V'中任何两个顶点都可以由 E中的某一条边连接起来，那么称 C是一个团。

定义2 极大团在给定图G=(V,E)中，如果存在一个团V"⊆V，并且不存在任何一个顶点v ∊ ( VV")，使得{v}∪V"成为一个更大的团，那么称V"是一个极大团。

定义3 团概率在给定的概率图G = ( V,E,β)中，如果存在一个团 C，那么用 clq(C,G)来表示团C的团概率，clq(C,G)的实际意义为团C所有边上权值的乘积。

定义4 α-团在给定的概率图G = ( V,E,β)中，如果存在一个团 C，对于给定参数 0<α<1，有clq(C,G)≥α，那么称团C为一个α-团。

定义5 α-极大团在给定的概率图G=(V,E,β)中，如果存在一个α-团C，并且不存在任何一个顶点v ∊ ( VC)，使得{v}∪C是一个 α-团，那么称α-团C为α-极大团。

定理1在给定图G=(V,E)中，对于顶点v，如果有Cn(v)=m，那么包含顶点v的极大团顶点规模不超过m+1。

证明：采用反证法。如果有顶点v∊C，且极大团C顶点规模为m+2，则对于任一顶点u∊C，有d(u)≥m+1，那么可以得到Cn(v)=m+1，这和条件相违背。

问题定义给定概率图G =(V,E,β)、阈值α、整数K，在概率图G上枚举出顶点规模前K大的α-极大团。

1.2 相关算法

Enumk算法[13]在确定图上枚举 Top-K 极大团，该算法并没有使用近似贪心的Max K-Cover算法去查询所有的极大团，而是保留K个候选团，通过不断更新大小为K的结果集来保存结果。在结果集存满之后，极大团是否能够存进结果集则依赖于Enumk算法建立的PNP-Index。

PNP-Index 记录着团中的私有顶点，算法会尽量将结果集中私有顶点少的极大团替换掉，使得结果集中极大团的顶点覆盖率尽可能高。但是该算法在维护PNP-Index时需要不断遍历结果集中的顶点去寻找每个团的私有顶点，当图规模较大或者稠密时，效率会很低。

同样是求顶点覆盖率最大的Top-K极大团，Wu等人[14]在2020年提出了一种高效枚举Top-K极大团的TOPKLS算法。该算法利用 ECC策略对每一个顶点进行标记，对于任何一个极大团，只有团中所有顶点的标记都满足要求，该团才可以作为结果被输出。此外，TOPKLS算法会利用启发式算法确定需要删除的极大团，保证结果集中极大团的顶点覆盖率尽可能高。

Hao等人[15]证明了形式概念和极大团之间的等价关系，从图中构造出极大团的搜寻指标，将原来的Top-K极大团枚举问题转变成了形式概念检测问题。在此基础上，Hao等人设计了一种Wise-Greedy算法来进行形式概念的检测。相较于枚举极大团，形式概念检测这种软计算只需要利用堆栈在图上提取出Top-K极大团即可，效率要更高。

Arko Provo Mukherjee等人[16]在2015年提出了在概率图上枚举极大团的MULE算法。该算法依赖C、I、X三个升序集合来进行DFS和递归，并会从集合I中选择顶点逐步向集合C中添加，同时保持集合C中顶点能够构成一个α-团。在集合C能够构成一个α-极大团之前，算法会回溯去探索其他可能扩展集合C的顶点，直到所有可能的搜索路径被探索。MULE算法会将图中所有α-极大团都枚举出来，但是其中相当一部分都是小规模团，这些团能够提供的信息量非常有限，并没有研究的价值。

综上所述，确定图上的Top-K极大团枚举是返回顶点覆盖率最高的K个团；概率图上的Top-K极大团枚举是返回团概率最大的K个团。本文重新定义了概率图上的Top-K极大团枚举问题，用于返回团概率大于给定阈值的前K个规模最大的极大团。

2 高效的枚举算法

2.1 T op-KC算法

本文提出了 Top-KC算法，该算法用于在概率图上枚举基于顶点规模的Top-K α-极大团。该算法利用C、I、X三个升序集合递归枚举α-极大团，同时，算法维护一个大小为K的结果集保存满足条件α-极大团。算法1为Top-KC算法的伪代码。Top-KC算法首先会给候选集I初始化（第1-3行），集合I中升序放入所有顶点的编号，最后调用算法 Enum_Clique进行枚举（第 4行）。Enum_Clique算法中，如果集合I和集合X都为空，则根据结果集的状态判断如何对其进行更新（第1-7行）。如果当前集合C不是α-极大团，从候选集I选择一个点加入集合C，并且更新集合C的团概率、候选集I、集合X，进入下一层运算（第8-14行）。更新算法UpdateI和UpdateX的核心是在对应集合中找出可能和C构成极大团的顶点，详情可参考文献[14]，本文不再赘述。

给定阈值 α=0.4、整数 K=2，下面用图1中的概率图G为例说明Top-KC算法的流程，图2展示了调用 Top-KC算法时结果集的更新过程。初始化的集合 C和集合 X为空集，集合 I={A,B,C,D,E,F,G,H,I}。如图2中(1)所示，以一号顶点A作为起始顶点枚举到的第一个α-极大团是{A,B},此时结果集为空，所以团{A,B}直接存入。从顶点B开始得到的第一个α-极大团是{B,C,D}，此时结果集未满，团{B,C,D}直接存入。以顶点B为起始顶点能够枚举到的第二个 α-极大团是{B,D,E}，此时结果已满，而团{B,D,E}的顶点规模比结果集中的团{A,B}更大，所以团{B,D,E}将团{A,B}替换。以顶点 B为起始顶点枚举到的最后一个α-极大团是{B,F}，但是由于结果集已满且所有结果的顶点规模都大于2，所以团{B,F}被舍弃掉。算法回溯到 C={F}、I={G,H,I}的状态，此层递归只能得到{F,G,H,I}一个团。由于此时结果集中的顶点规模最小的团大小为 3，所以可以用{F,G,H,I}将其替代，最终结果集中存放的两个 α-极大团是{F,G,H,I}和{B,C,D}。

在利用Top-KC算法对图1中的概率图进行α-极大团枚举的过程中，一共枚举了 5个团，并对结果集中的数据进行了2次替换。

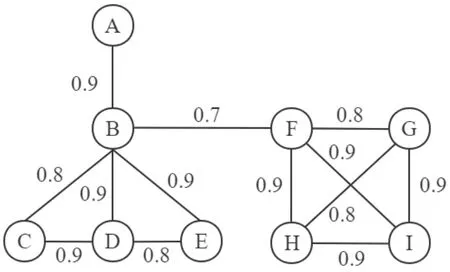
图1 概率图GFig.1 Un certain graph G

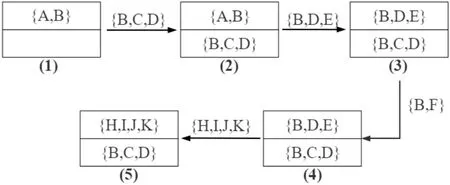
图2 结果集的更新过程Fig.2 The process of updating the result set

2.2 T op-KCD算法

虽然Top-KC算法利用顶点升序限制搜索空间避免了重复枚举，但还是需要枚举所有的团并进行比较才能得出结果。Top-KCD算法的基本思想是在枚举的过程中先处理度大的顶点，这样可以尽早得到顶点规模大的极大团，还能避免不必要的计算和替换工作。算法2详细介绍了Top-KCD算法的流程。Top-KCD算法会利用顶点的度对顶点进行降序排序并重新编号（第1-2行），编号完成后调用算法Enum_Clique枚举α-极大团。Enum_Clique算法会对新添加进集合C的顶点u进行判断，如果d(u)≥ Smallest(Rs).size ，则说明继续计算下去可能找到顶点规模大于Smallest(Rs).size的α-极大团，否则直接跳出此次循环（第9-16行）。

图3展示了按照度降序排序后顶点的处理顺序，图4展现了Top-KCD算法处理图G时结果集的更新过程。以一号顶点B为初始顶点，得到的第一个α-极大团是{B,F}，此时结果集为空，直接存入即可。以B为初始顶点可以将集合C拓展成{B,D}，{B,D}能够拓展出的第一个α-极大团是团{B,C,D}，此时结果集未满，依旧是直接存入。{B,D}能够拓展出的第二个α-极大团是团{B,D,E}，此时的结果集已满并存在顶点规模更小的α-极大团{B,F}，所以用{B,D,E}将其替代。以顶点B为初始顶点的最后一次递归中I={A}，但是d(A)=1,即顶点A能够构成的最大的团顶点规模是2，而结果集中最小的顶点规模是 3，所以不需要继续计算，算法直接进入下一次循环。以顶点F为初始顶点，只能得到一个 α-极大团{F,G,H,I}，此时结果集中顶点规模最小的团大小为 3，所以用{F,G,H,I}将其替换。至此枚举结束，结果集的状态如图4中(4)所示。

图3 按照度降序排序后顶点的处理顺序Fig.3 The order in which vertices are processed after sorting by degree in descending order

图4 结果集的更新过程Fig.4 The process of updating the result set

在利用Top-KCD算法对概率图G进行Top-K α-极大团枚举的过程中，一共枚举了{B,F}、{B,C,D}、{B,D,E}、{H,I,J,K}4个α-极大团，对结果集进行了2次结果更替。

2.3 T op-KCC算法

虽然Top-KCD算法成功减少了Top-K极大团求解过程中所枚举的极大团数量，但也暴露了一个问题，即利用度进行优化的稳定性不高。图1中d(B)>d(F)，但是团{F,H,I,J}的顶点规模却更大，这样仍会导致不必要的替换。Top-KCC算法依据Core-Number对顶点进行降序排序并重新编号。对于任意顶点u，d(u)=h只能代表顶点u与h个顶点相连，是一对多的关系，这h+1个顶点之间关系并不一定紧密；而 Cn(u)=h则能够保证顶点u∊B，且对于连通子图B中的任一顶点v来说，都有d(v)≥h，这是多个顶点之间的相互联系，是多对多的关系。所以基于Core-Number的优化策略会比基于度的优化策略效果更好。算法 3是Top-KCC算法的伪代码，Enum_Clique算法会对新添加进集合C的顶点u进行判断，根据定理1，如果Cn(u)+ 1 ＞ S mallest(Rs).size ，则说明继续计算有可能找到顶点规模大于Smallest(Rs).size的 α-极大团，否则直接跳出此次循环（第9-16行）。

图5展示了按照Core-Number降序排序后顶点的处理顺序，图6展示了Top-KCC算法处理图G时结果集的更新过程。Top-KCC从一号顶点F开始枚举，得到第一个 α-极大团{F,G,H,I}，此时结果集为空，{F,G,H,I}直接存入。以顶点 F为初始顶点枚举到的第二个α-极大团是团{B,F}，此时结果集未满，直接存入即可。以顶点B为初始顶点进行枚举，得到的第一个α-极大团为{B,C,D}，{B,C,D}可以替换掉结果集中的团{B,F}。接着，算法回溯到集合C={B,C}、I={E,A}的情况，由于Cn(E)=2，即由顶点E构成的极大团顶点规模最多是3，并没有大于Smallest(Rs).size，所以不再继续计算。同理，顶点A的情况也不会进行计算。整个枚举过程一共只枚举了3个极大团，只进行了一次替换操作。

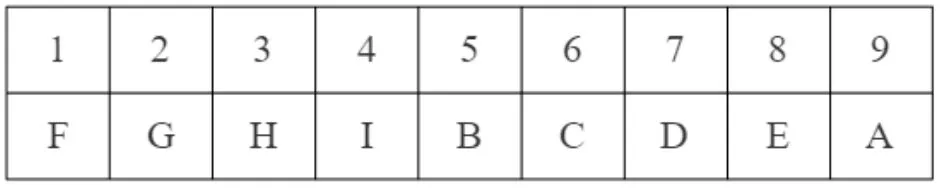
图5 按照Core-Number降序排序后顶点的处理顺序Fig.5 The order in which vertices are processed after sorting by Core-Number in descending order

图6 结果集的更新过程Fig.6 The process of updating the result set

2.4 算法分析

Enum_Clique算法可以被看成一个搜索树，每一次调用都是搜索树的一个顶点，在顶点个数为 n的图中，Enum_Clique算法的时间复杂度是O(n· 2n)。对于Top-KCD来说，依据度排序的时间复杂度为 O (n· log2n)，所以整体算法的时间复杂度是 O (n· 2n)。Top-KCC 算法中求取 Core-Number可以在线性时间内完成，所以整体算法的时间复杂度也是 O (n· 2n)。

3 实验

3.1 实验环境

本实验所用的计算机配置如下：处理器为Intel(R)Core(TM)15-8300H CPU@2.30GHz，内存(RAM)8.00GB，操作系统为Windows 10。由于已有方法不能解决本文提出的Top-K极大团枚举问题，本文实验中用于比较的算法均为正文中提出的算法，包括基础算法Top-KC、基于度的优化算法Top-KCD、基于Core-Number的优化算法Top-KCC。算法均采用 C++实现，通过Visual S tudio 2019编译运行，解决方案为Release，解决方案平台是Win32。

3.2 数据集

本文采用的数据集为 11个大型概率图数据集。其中数据集web-Google是来自于Google的网络图，Email-EuAll是欧盟研究机构的电子邮件网络，WikiTalk是维基百科对话交流网络，Email-Enron是安然公司的电子邮件通讯网络、Slashdot0811是Slashdot资讯科技网站2008年11月的社交网络。

表2列出了这些数据集的基本信息，其中：|V|代表图中顶点个数，|E|代表图中边的个数。

表2 数据集Tab.2 D ateset

3.3 算法性能比较分析

本实验的评价标准包括：1）求解过程中枚举极大团的数量；2）找到 Top-K个 α-极大团的时间。为了比较算法的性能，实验给定阈值α=0.3，在 K=15、K=10、K=5三种情况下分别对三种算法进行测试。

3.3.1 求解过程中枚举极大团的数量

算法统计了在枚举Top-K α-极大团的过程中一共计算了多少个极大团，极大团的数量反映了枚举过程中遍历的路径数目，路径越少则算法越优。表3展示的是当α=0.3、K=15时，不同数据集用三种算法所需要枚举的极大团个数。由于没有任何优化，Top-KC算法会将图中所有满足条件的 α-极大团枚举出来才能知道哪些是最后的结果。 T op-KCD算法枚举的极大团个数远小于Top-KC算法，对于 05citeseerx、05cit-Patent和cit-Patents等数据集来说，前者的枚举数量都只有后者的千分之一。Top-KCC算法更是将枚举极大团的数量限制在了100以下。

表3 K=15 时整个枚举过程中计算α-极大团的数量Tab.3 The number of α-maximal cliques calculated during the entire enumeration process when K=15

表4展示了 K=10时，三种算法在计算过程中枚举的α-极大团个数。随着K的降低，优化算法枚举的极大团数量有了一定程度的减少，相比于K=15，K=10时，Top-KCD算法的平均枚举数量减少了20%，Top-KCC算法的平均枚举个数减少了32%。

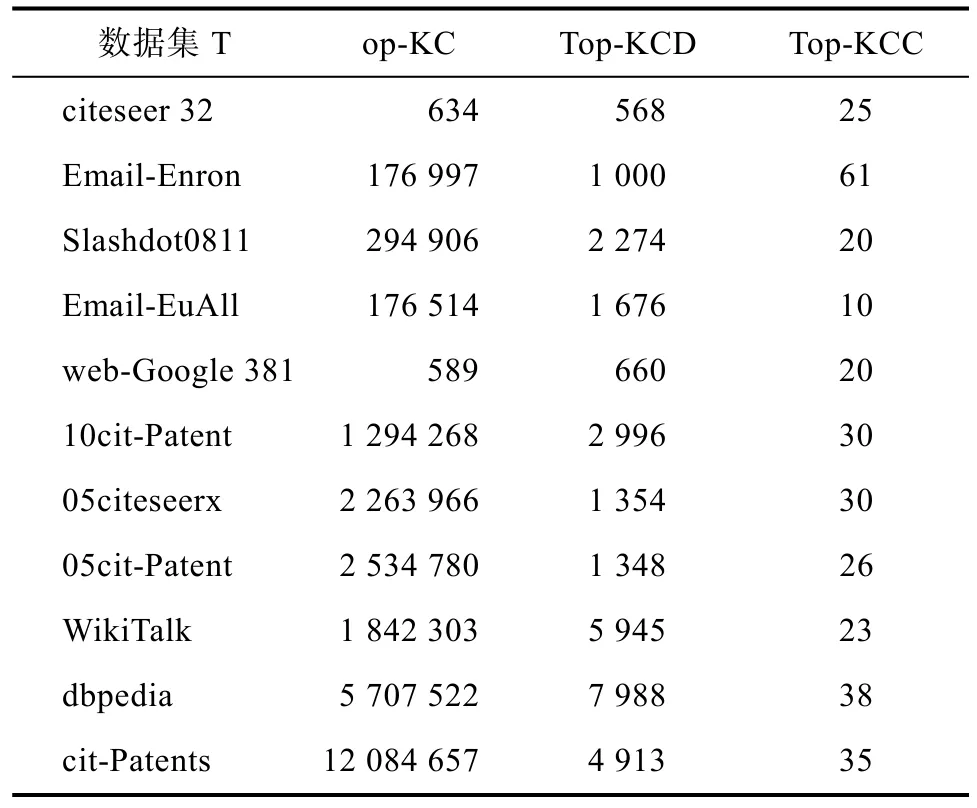
表4 K=10时整个枚举过程中计算α-极大团的数量Tab.4 The number of α-maximal cliques calculated during the entire enumeration process when K=10

表5展示了K=5时，三种算法在计算过程中枚举的α-极大团个数。对比表3、表4、表5可以发现，Top-KCD算法和Top-KCC算法枚举的极大团个数会随着K值的变小而变小。

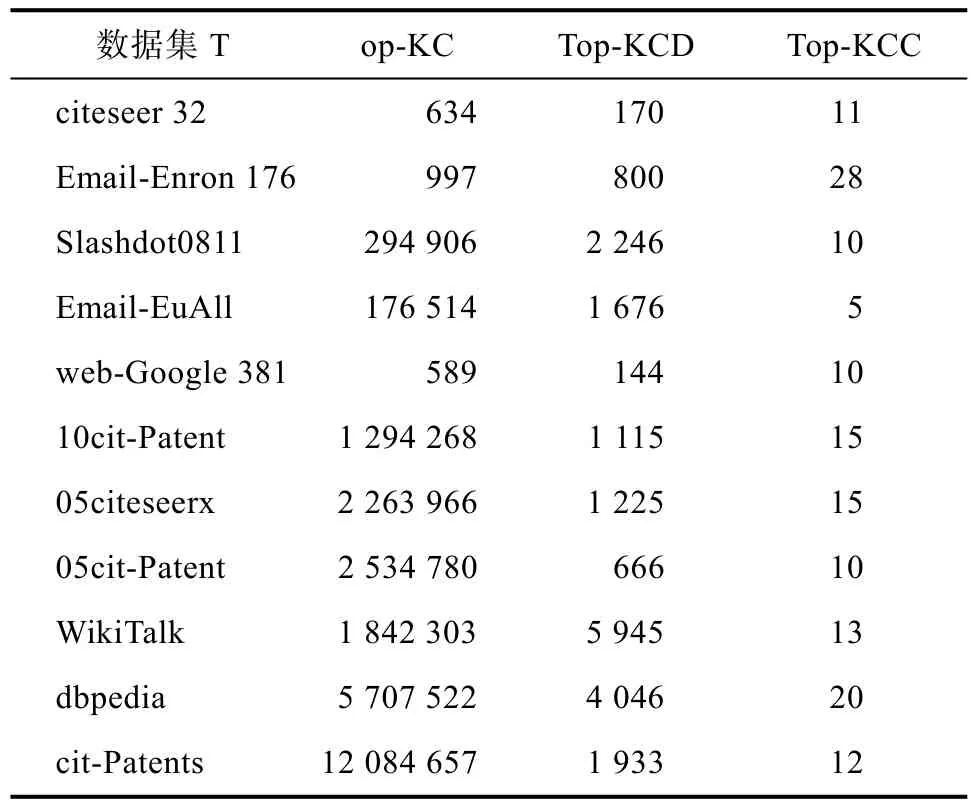
表5 K=5时整个枚举过程中计算α-极大团的数量Tab.5 The number of α-maximal cliques calculated during the entire enumeration process when K=5

3.3.1 枚举极大团的时间

枚举Top-K α-极大团的时间能最直观地表现出算法的性能差别。表6展示了K=15时，三种算法枚举出Top-K α-极大团所需要的时间。在K=15的时候，Top-KCD算法计算的平均速度比Top-KC算法快了1.5倍，而Top-KCC算法计算的平均速度比Top-KC算法快了3.2倍。在计算数据集Email-EuAll时，两种优化算法的表现最好，Top-KCD算法比 Top-KC算法快了 60倍，Top-KCC算法比Top-KC算法快了400倍。

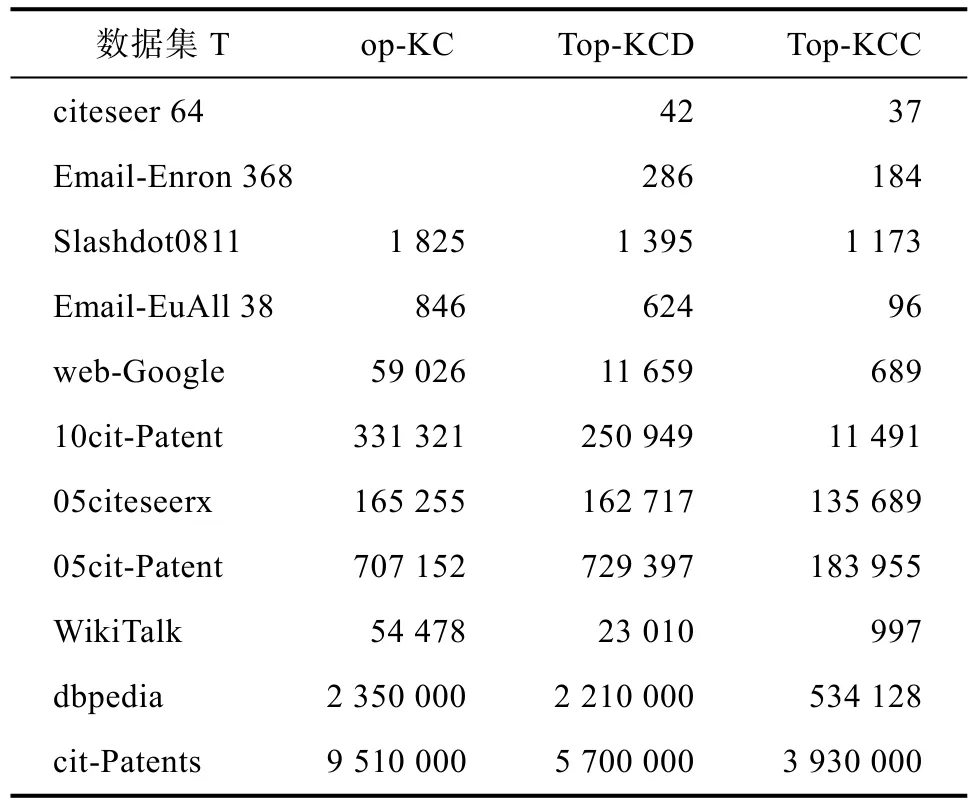
表6 K=15 时枚举Top-K α-极大团的时间Tab.6 The time of enumerating top-k α-maximal clique when K=15

表7展示了K=10时，三种算法枚举出Top-K α-极大团所需要的时间。K=10时，Top-KCD算法计算的平均速度比 Top-KC算法快了 1.2倍，Top-KCC算法计算的平均速度比Top-KC算法快了2.6倍。

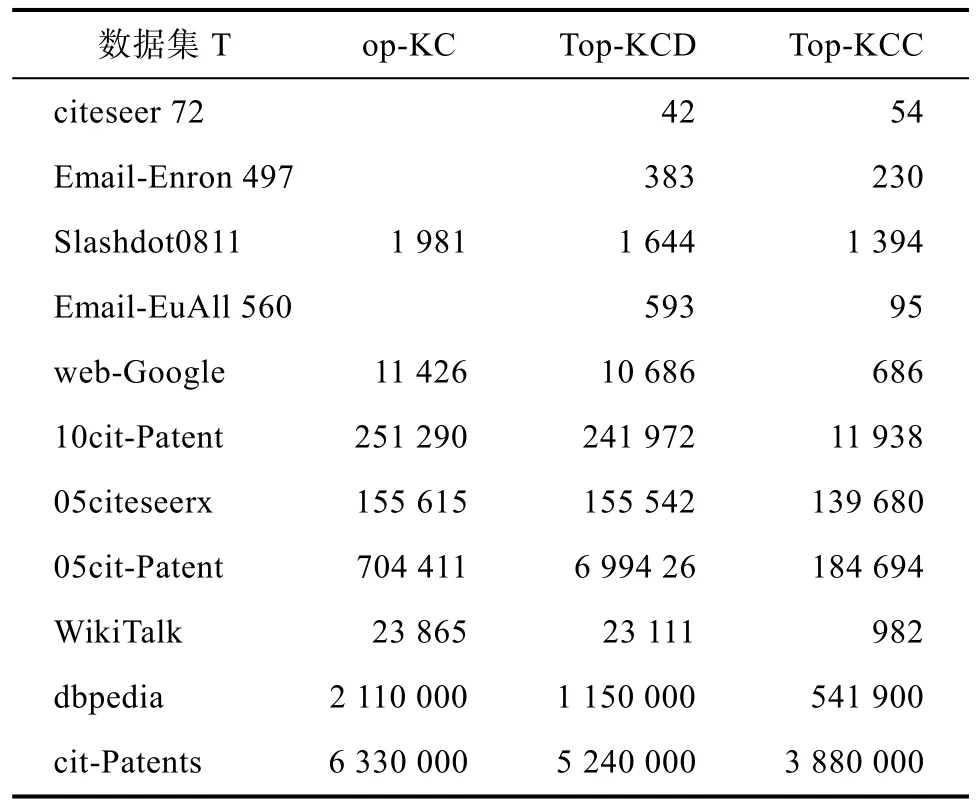
表7 K=10 时枚举Top-K α-极大团的时间Tab.7 The time of enumerating top-k α-maximal clique when K=10

表8展示了K=5时，三种算法枚举出Top-K α-极大团所需要的时间。K=5时，Top-KCD算法计算的平均速度比 Top-KC算法快了 1.5倍。Top-KCC算法计算的平均速度比Top-KC算法快了3倍。随着K的减小，Top-KCD的优化效果慢慢减弱，而 Top-KCC算法始终保持在一个稳定水平。

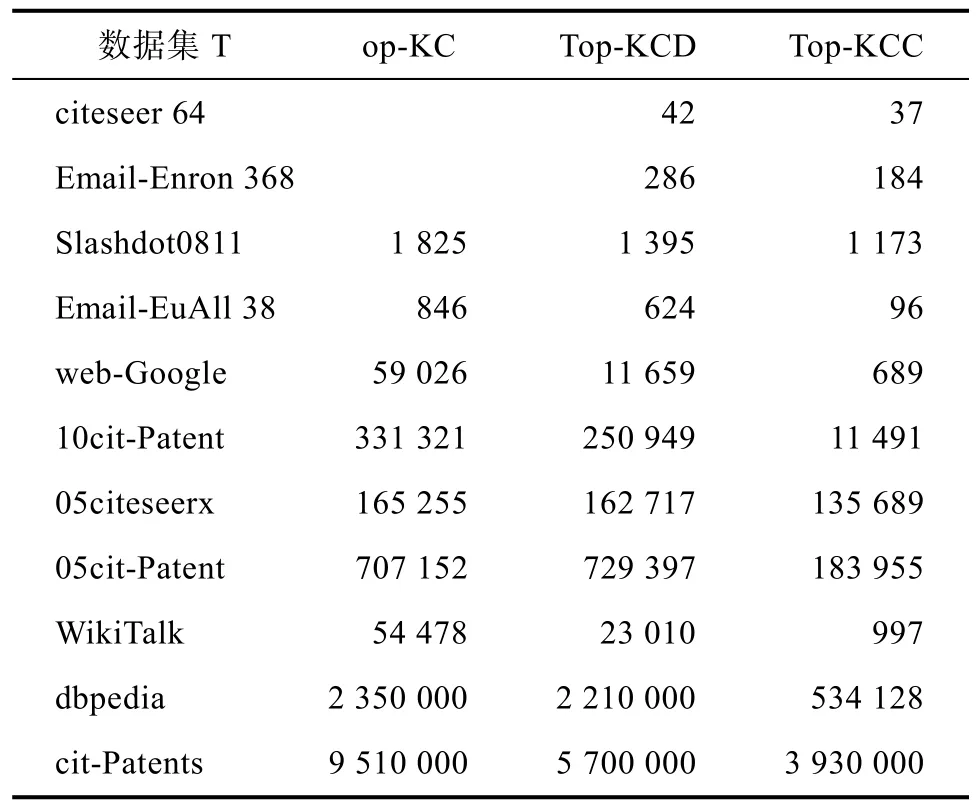
表8 K=5时枚举Top-K α-极大团的时间Tab.8 The time of enumerating top-k α-maximal clique when K=5

4 结论

针对现有Top-K α-极大团枚举会丢失大规模团的问题，本文重新定义了概率图上的Top-K极大团枚举，并提出了Top-KC算法。在此基础上，本文对该算法提出了分别利用度和 Core-Number进行优化的Top-KCD和Top-KCC算法。两种优化策略都是通过排序和剪枝减少了不必要的枚举和替换操作。实验结果表明，Top-KCD算法计算的平均速度是 Top-KC算法的 1.5倍，Top-KCC算法计算的平均速度是Top-KC算法的3.2倍，两种优化都提高了Top-K α-极大团的枚举效率。