一种求解软硬件划分问题的混合编码二进制差分演化算法
2021-07-30翟庆雷朱晓斌
翟庆雷,朱晓斌
(1. 河北地质大学 信息工程学院,河北 石家庄 050031;2. 石家庄文化传媒学校,河北,石家庄 050000)
0 引言
随着嵌入式系统的广泛应用,软硬件协同设计已成为一个重要的研究问题。硬件部分执行速度快,但是成本费用较高,花费的资源较多;软件部分虽然执行速度较慢,但成本花费较低,操作相对灵活。合理地把嵌入式系统中的组件根据需求进行软、硬件协同划分执行,对整个系统的性能将有很大的提升,因此软硬件划分(hardware/software partitioning,HW/SW)已成为软硬件协同设计中的一个重要问题。
近年来,基于启发式算法求解大规模HW/SW问题逐渐成为了一个研究热点。例如Arato等人[1]提出了一个求解HW/SW问题的2D搜索启发式算法,该算法利用了HW/SW问题特点,因而能够快速地找到高质量的解。Wu等人[2]将HW/SW问题看成带有通信成本的扩展 0-1背包问题,提出了求解该问题的一个 1D搜索启发式算法。该方法不仅提高了算法的性能,而且降低了算法的时间复杂度。Wang等人[3]提出了HEUR算法,并利用它给出了求解HW/SW问题的一种新方法。该方法首先忽略通信成本,将HW/SW问题看作是一个标准 0-1背包问题,求得其解作为原问题的一个潜在解;然后,再根据通信成本对潜在解进行调整,从而得到HW/SW的一个满足约束条件的可行解。虽然HEUR算法比1D搜索启发式算法[2]在解的质量上得到了很大提升,但是利用禁忌搜索对解作进一步的优化处理,在求解大规模HW/SW 实例时也是非常耗时的。正是由于HW/SW 的重要性和困难性,如何快速高效地求解该问题是一个值得研究与探讨的重要问题。
差分演化算法(differential evolution,DE)[4]是Storn和Price为求解切比雪夫多项式而提出的一种著名演化算法,是一个基于实数编码的演化算法,非常适合于求解连续域上的最优化问题。为了使 DE能够求解离散域上的最优化问题,贺等人[5]基于数学变换思想引入“辅助搜索空间”和“个体混合编码”等概念,通过定义一个特殊的满射变换,在辅助搜索空间的作用下将连续域上的高效差分演化搜索变换为离散域上的同步演化搜索,由此提出了第1个二进制差分演化算法:具有混合编码的二进制差分演化算法(binary differential evolution algo rithm with hybrid encoding,HBDE)。HBDE不仅完全具有DE的各种特性和所有优点,而且非常适用于求解离散域上的最优化问题,并且在求解具有单连续变量的背包问题[6]和多维背包[7]中表现出优异性能。为此,本文研究如何利用HBDE高效求解HW/SW。
1 HW/SW 问题的定义和数学模型
HW/SW的定义一般描述为:给出一个无向图G=(V,E),其中V和E分别表示节点集和边集。s(vi)和h(vi)分别表示节点vi的软件成本和硬件成本,简记为si和hi;边(vi,vj)的权值c(vi,vj)表示当节点vi与vj属于不同划分时它们之间的通信成本,简记为cij。设P={VH,VS}为G的一个软硬件划分,其中VH表示用硬件实现的节点集合,VS表示用软件实现的节点集合,VH∩VS=Ø 且VH∪VS=V。P的边集为EP={(vi,vj)|(vi∊VS,vj∊VH)ˇ(vi∊VH,vj∊VS)}。HW/SW的目的是求一个划分P在软件成本与通信成本之和不超过给定值R的前提下使得硬件成本最小。
令X= (x1,x2,…,xn)∊ { 0,1}n,n为节点数,则X对应一个软硬件划分,xi= 1 表示节点vi由软件实现,xi= 0 表示节点vi由硬件实现,则HW/SW问题的整数规划模型为:
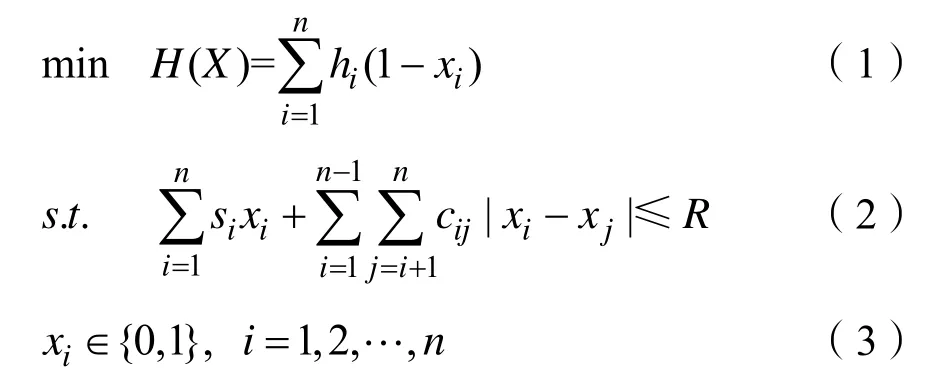
由 HW/SW 的整数规划模型可知,其计算复杂度为O(n2)。需要注意的是,一个n维0-1向量只有满足式(2)时才是HW/SW的一个可行解,否则是HW/SW的一个不可行解。
2 具有混合编码的二进制差分演化算法
与 DE[4]类似,HBDE[5]的一次迭代进化由变异操作、交叉操作和选择操作共同完成,它们的实现方法简述如下:
在变异操作中,对于种群中的第i个个体Yi=(yi1,yi2,…,yin)∊[-A,A]n,A是正实数,随机选取种群中3个不同个体Yr1= (yr1,1,yr1,2 ,…,yr1,n),Yr2= (yr2, 1,yr2, 2 , …,yr2,n),Yr3= (yr3,1,yr3, 2 ,…,yr3,n),将其中Yr2和Yr3的差缩放FS倍后与Yr1求和,产生中间个体Zi= (zi1,zi2,… ,zin)。变异操作的计算式为:
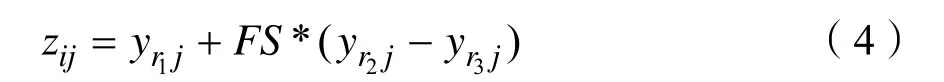
其中,0<FS<1为缩放因子,r1,r2和r3是在范围[1,N]内的三个互不相同并且不等于i的随机整数,N为种群规模。
HBDE的交叉操作是针对每一维分量产生一个随机小数r,如果r<CR(交叉因子)则进行交叉操作。交叉操作产生的中间个体不妨仍设为Zi=(zi1,zi2,…,zin)∊[-A,A],则交叉操作的计算式为:
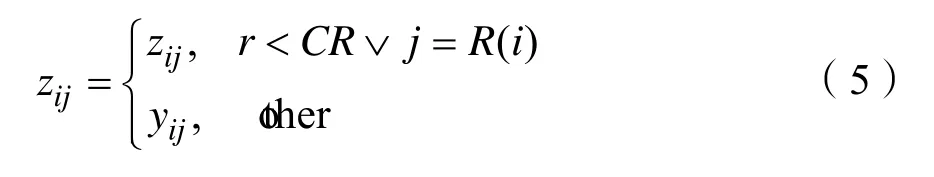
由于DE中的变异操作是实数运算,不能直接应用于求解组合优化问题。为此,贺等人[5]利用映射的方法将实数编码转换为0-1编码。设个体Zi=(zi1,zi2,…,zin)∊[-A,A],A是正实数,Wi=(wi1,wi2,…,win)是n维0-1向量,则HBDE利用(6)式给出的满射函数Ψ由Zi得到Wi:

HBDE的选择操作采用的是贪心策略,即由(5)产生的中间个体Zi比当前个体Yi更优时,Zi作为下一代种群的第i个个体,否则Yi作为下一代种群的第i个个体。不妨设 minh(Y) ,Y∊S⊆Rn表示一个最小优化问题,则HBDE的选择操作的计算式为:
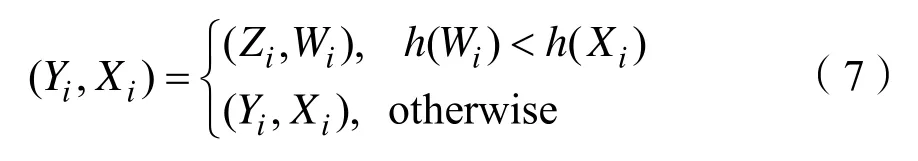
其中,X=(xi1,xi2,…,xin)∊{0,1}n是个体Yi由Ψ得到的0-1向量。Wi=(wi1,wi2,…,win)∊{0,1}n是Zi由Ψ得到的0-1向量。
3 求解HW/SW问题的方法
由于 HW/SW 是一个约束优化问题,在利用HBDE求解时不可避免地将会产生不可行解。为此,下面首先基于贪心策略提出处理HW/SW的不可行解的修复与优化算法GROA,然后在此基础上给出基于HBDE求解HW/SW的启发式算法。
3.1 基于贪心策略的修复与优化


3.2 基于HBDE求解HW/SW


4 仿真实验
本文所有的计算均在配置为 Intel(R)Core(TM)i5-4210 CPU @ 1.70GH z和8GB RA M的微型计算机上进行,操作系统为 W indows 10,编程语言为C,编译环境为Code::Blocks 17.12,使用Python在编译环境JetBrains PyCharm绘图。
4.1 HW/SW 实例与算法参数设置
本文所用的11个HW/SW测试实例来自于文献[10]。在每个实例中,n和m分别为无向图G=(V,E)中的节点数和边数,size表示实例的规模,且size= 2 ×n+3×m。在表1中详细给出了11个HW/SW测试实例。

表1 11个HW/SW实例Tab.1 1 1 HW/SW instances
在本文中,所有算法的种群规模均设置为N=30,迭代次数MIR=n(n为节点个数)。在HBDE中,–A=5和A=5分别表示的每个个体向量中的每一维分量取值的上界和下界,CR和FS分别为变异因子和缩放因子。在GA中,Pc=0.8和Pm=0.001分别为交叉因子和变异因子。
4.2 计算结果比较与分析
在本节中,利用HBDE和GA[11]对上述HW/SW实例进行计算,并对它们的计算结果进行比较。在表2中给出了算法对每一实例独立计算30次所获得的最好值为Best、平均值为Mean、标准差为Std。

表2 GA 和HBDE求解11个HW/SW实例的计算结果Tab.2 Calculation results of GA and HBDE for solving 11 HW/SW instances
从表2明显可以看出,就指标Best而言,对于实例1,3和4,HBDE与GA的结果相等,对于实例 6,HBDE的结果比 GA差,对于实例 2和7-11,HBDE的结果明显优于GA。就指标Mean而言,对于实例1和3,HBDE结果与GA相等,对于实例 2和 4-11,HBDE的结果优于 GA。就指标Std而言,对于实例1和3,HBDE与GA的结果相等,对于实例10,HBDE的结果比GA差,对于实例 2,4-9和 11,HBDE的结果明显优于GA。因此通过以上分析我们可知,基于 HBDE求解HW/SW是一种高效可行的方法,并且其性能优于经典的GA。
5 总结与展望
本文首先给出了基于贪心策略处理 HW/SW的不可行解的修复与优化算法GROA,然后利用具有混合编码的二进制差分演化算法(HBDE)求解HW/SW的一般框架,最后比较了HBDE和GA求解11个HW/SW实例的计算结果。计算结果表明,HBDE是一种求解HW/SW问题的高效算法。由于 HW/SW 在软硬件协同设计中的重要性,对其快速高效求解的研究一直是一个重要的方向。为此,今后将尝试利用新提出的演化算法,例如郊狼优化算法[12](coyote opti mization algorithm,COA)、浣熊优化算法[13](raccoon optimization algorith m,ROA)和松鼠搜索算法[14](squirrel search algorithm,SSA)等求解HW/SW问题,进一步探讨高效求解HW/SW问题的新方法。
