Research on refined reconstruction method of airfoil pressure based on compressed sensing

Xuan Zhao , Lin Du , Xuhao Peng , Zichen Deng a , , e, Weiwei Zhang , ∗

a College of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China

b National Key Laboratory Science and Technology on Aerodynamic Design and Research, Northwestern Polytechnical University, Xi’an 710072, China

c School of Mathematics and Statistics, Northwestern Polytechnical University, Xi’an 710129, China

d MIITKey Laboratory of Dynamics and Control of Complex Systems, Northwestern Polytechnical University, Xi’an 710072, China

e School of Mechanics, Civil Engineering and Architecture, Northwestern Polytechnical University, Xi’an 710129, China

Key words: Pressure test Compressed sensing Proper orthogonal decomposition Pressure field reconstruction

A B S T R A C T The placement of pressure taps on the surface of the wind tunnel test model is an important means to obtain the surface pressure distribution. However, limited by space location and experimental cost, it is difficult to arrange enough pressure measuring taps on the surface of complex models to obtain complete pressure distribution information, thus it is impossible to obtain accurate lift and moment characteristics through integration. The paper proposes a refined reconstruction method of airfoil surface pressure based on compressed sensing, which can reconstruct the pressure distribution with high precision with less pressure measurement data. Tests on typical airfoil subsonic flow around flow show that the accuracy of lift and moment after the pressure integration reconstructed by 4-8 measuring points can meet the requirements of the national military standard. The algorithm is robust to noise, and provides a new idea for obtaining accurate force data from sparse surface pressure tests in engineering.

Wind tunnel test is an important means to obtain complex flow characteristics. The load measurement in the existing wind tunnel test mainly includes direct force measurement and surface pressure measurement. The wind tunnel scale model of the aircraft is therefore divided into two types: force measurement model[1]and pressure measurement model [2] . The force measurement model can obtain the integrated load characteristics through the strain balance, but cannot obtain the distribution information and important flow characteristics such as transition, separation, and shock wave. For dynamic experiments (such as dynamic derivative experiments), the acquisition of unsteady loads is a difficult point.To measure the force with a balance, it is necessary to remove the inertial force and damping force, and the experimental design is difficult and the measurement accuracy is not high. The pressure measurement model can obtain the normal stress distribution of the airfoil surface, and if the shear stress sensor is installed, the friction force distribution can also be obtained. The lift, moment,and drag information can also be obtained by integrating the distributed load. However, this requires sufficient pressure measuring holes on the airfoil surface, which is limited by the space location and experimental cost. In many cases, it is difficult to arrange enough measurement holes. For example, the model’s flaperons,the trailing edge of the airfoil, and the high-speed wind tunnel model have a larger shrinkage and a smaller model. The existing methods directly integrate a small amount of pressure measurement results, and it is difficult to guarantee the accuracy of the obtained lift and torque.

Therefore, it is necessary to develop a method to reconstruct the flow field information of the full airfoil surface using the flow field data of limited measurement points. However, in many engineering applications, the use of limited measurement data to estimate the flow field structure is an important challenge. For example, accurate estimation is the core of active flow control [3–6] ,which strongly promotes the development of next-generation technologies, from energy-saving, low-drag vehicles [7] to efficient turbines [8] and internal combustion engines [9] . The ability to reconstruct important flow characteristics from restricted observations is also crucial in many applications such as cardiac blood flow modeling [ 10 , 11 ], ship wake identification [12] , and climate science [13] .All these applications rely on the estimation of complex fluid flow structures based on limited measurements. This paper is to solve this problem by using machine learning and compressed sensing technologies [ 14 , 15 ], which are also applied to flow field classification [16–19] .

Compressed sensing (CS) theory breaks the constraints of Shannon’s sampling theorem, and can achieve high-precision complete signal reconstruction with less data. Once CS technology is proposed, it has attracted the interest of researchers and is widely used in geography [20] , aerospace [21] , communications [22] and other fields. In the field of fluid mechanics, many related researches have been carried out on data reconstruction based on compressed sensing. Kutz et al. [16] proposed an integrated compressed sensing and machine learning method for flow field reconstruction around a cylinder. Bai et al. [23] used compressed sensing technology to compress and reconstruct turbulent particle images for the NACA4412 airfoil. The results showed the feasibility and practicability of using compressed sensing to reconstruct the compressed or finite time support particle image velocity measurement flow field data. Brunton et al. [17] proposed a method based on compressed sensing and low-order libraries to identify the bifurcation parameterβin a nonlinear dynamic system and reconstruct the related low-order dynamics. Callaham et al. [24] studied the sparse representation on a variety of complex fluid data sets,including low Reynolds number cylinder vortex shedding, mixing layer, and geophysical data sets. For complex multi-scale flows,they also introduced a local Sparse estimation method of space block.

The increase in the scale and resolution of modern numerical simulations has provided a large amount of simulation data. Therefore, this paper uses a data-driven method to calculate the pressure distribution data under different airfoils and different working conditions in advance, and extract the pressure distribution data using the proper orthogonal decomposition method. Then, based on the compressed sensing algorithm, the pressure distribution data of the same airfoil in various states and the pressure distribution data of variable airfoils in the same state were reconstructed. This paper compares the influence of the number of measurement points on the reconstruction accuracy, and verifies the robustness of the method to noise by introducing measurement noise.

The algorithm framework is shown in Fig. 1 . The research content is mainly divided into the following four aspects. (1) Use computational fluid dynamics (CFD) to calculate the pressure distribution of the same airfoil in various states (NACA0012 airfoil) and variable airfoils in the same state under the condition of subsonic speed. (2) Construct the sparse basis function of the pressure field based on the proper orthogonal decomposition (POD) technology.(3)Selection of pressure measuring point position on airfoil surface: the best measuring point position is obtained through training through particle swarm optimization (PSO) algorithm. (4) Flow field reconstruction based on compressed sensing technology.

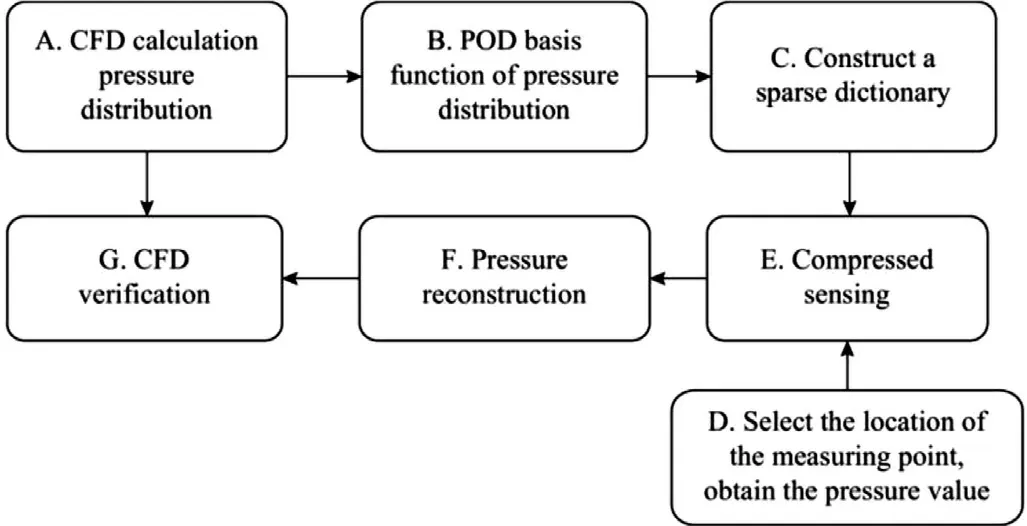
Fig. 1. Algorithm framework process.

Fig. 2. First eight order basis functions obtained by POD.

In this paper, the CFD solver adopts the Jameson central scheme’s finite volume method for discretization [25] . In order to solve the N-S equation, the dual time advance method is used. The real time adopts second-order precision backward difference, and the pseudo time adopts implicit Gauss-Seidel iteration.

POD [ 26 , 27 ] is a commonly used method of dimensionality reduction, which can project complex dynamics from a highdimensional discretization system to a low-dimensional system.The essence of this method is through Matrix transformation and orthogonal decomposition are performed on the flow field samples to obtain several orthogonal basis functions that minimize the sample residuals, which are used to describe the main laws of the flow field.

Compressed sensing allows the use of a small part of the measured value to reconstruct the signal, based on the fact that the signal has a sparse representation in an appropriate basis. In the field of fluid mechanics, the POD method can extract the temporal and spatial information and main modes of the flow. Therefore, we take the main mode of flow obtained by POD as the required sparse basis function, use POD to extract the characteristics of pressure distribution data, and build the basis function which is the sparse dictionary for compressed sensing.

PSO is an evolutionary computing technology. The basic idea of particle swarm optimization algorithm is to find the optimal solution through collaboration and information sharing between individuals in the group. The selection of the measurement point position will have a great influence on the reconstruction result. In the paper, the particle swarm optimization algorithm is used to obtain the penalty weight and the pressure measurement point position.These two processes are carried out simultaneously.

The basic steps are as follows. (1) Divide the pressure distribution data calculated by CFD into two parts, one is the training set and the other is the test set. The sparse basis function is obtained through POD on the training set. (2) In the training set, a part of the pressure distribution data is selected, based on the particle swarm optimization algorithm, the measurement points traverse all the points on the airfoil, and the flow field is reconstructed through the compressed sensing algorithm. The reconstruction error is used as the criterion, and finally a set of measurement point positions and penalty weight values that make the reconstruction error smaller are output. (3) Combining the obtained measurement point positions and penalty weight values, reconstruct the pressure distribution based on the compressed sensing algorithm in the test set.

In the paper, we combine POD and compressed sensing technology in pressure field reconstruction. Compressed sensing essentially seeks a regularized sparse solution by solving a computable convex optimization problem, using the L1 norm minimization of sparse coefficients. This sparse promotion L1 method is combined with the data-driven POD foundation to reconstruct the pressure distribution around the airfoil surface. The algorithm is as follows.

1 First, extract the sparse basis function of the sparse pressure field data obtained by CFD calculation through POD, that is, perform sparse representation of the pressure field data

2 Perform pressure point sampling on the airfoil surface, that is

In Eqs. (1) and (2) ,ψis the sparse basis function obtained by POD,sis the basis coefficient,φis the observation matrix, andyis the pressure value of the sampling point. Since the pressure field data can be sparsely represented by the sparse basis functionψ,the Eq. (2) is transformed into the following formula

1 Flow field reconstruction based on compressed sensing technology (convex L1 optimization)

The basis coefficient can be obtained by solving Eq. (4) , and the pressure distribution can be obtained by substituting it into Eq. (1) .

In this paper, we calculate 132 sets of pressure distribution data of the same airfoil in various states (NACA0012 airfoil,Ma= 0.1–0.6, angleof attackAOA= 0–11 °) and 400 sets of pressure distribution data of variable airfoils in the same state (Ma= 0.3,AOA= 2.5 °)through CFD. The pressure distribution is reconstructed based on compressed sensing technology in the above two cases. Finally,considering the influence of noise in practical engineering applications, the reconstruction results show that the method is robust to noise.

Basis function obtained based on POD method. In order to obtain 99% energy, at least 8 basis functions are required. Fig. 2 shows the obtained sparse basis functions, which are just for the typical case (same airfoil in various states). Our goal is to reconstruct based on a small number of measurement points. In the paper, the reconstruction is based on 4 measurement points (the reason why the number of measurement points is no longer reduced is because through numerical simulation, when reconstruction is performed with fewer measurement points, for most flow fields,the reconstruction results are relatively poor).

When reconstructing the variable state pressure distribution of the same airfoil, it is found that for some flow fields, the reconstruction results based on compressed sensing algorithm according to the 8 basis functions corresponding to 4 measurement points are poor, as shown in Fig. 3 a. The green solid line represents the CFD calculation result, and the red dashed line represents the reconstruction result. After comparing the basis coefficients obtained by L1 regularization, it is found that the value of the higher-order basis coefficients is relatively large, so this paper proposes to punish the higher-order basis coefficients based on the weight. Since the distribution of the basis coefficients has a statistical pattern,the penalty function is used to make the basis function distribution more consistent with the statistical pattern, so that the reconstruction performance on the test set is better. The strategy is to multiply the basis coefficient by the weight, and the weight value can be obtained through the PSO algorithm.

Figure 3 a shows the result of unweighted reconstruction through compressed sensing algorithm, the red dashed line is the reconstruction result, the green solid line is the CFD calculation result, the triangle represents the position of the measuring point.Fig. 3 b is the calculated unweighted basis coefficient. Fig. 3 c isthe reconstruction result of the compressed sensing algorithm after weighting the basis coefficients. Fig. 3 d shows the calculated weighted basis coefficients. The parameters of the flow field are as follows:Ma= 0.55,AOA= 2 °,Re= 5.40 ×106.

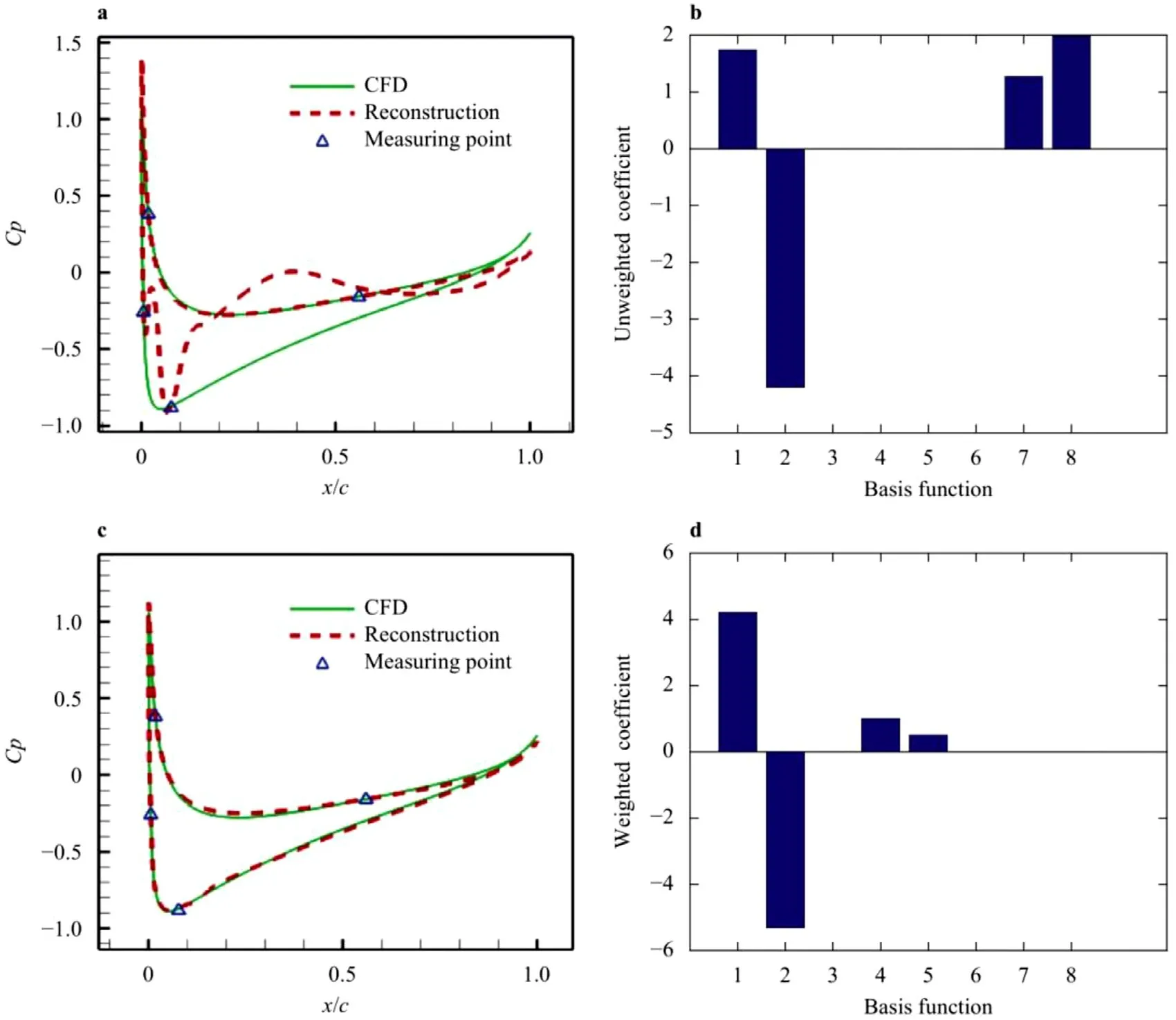
Fig. 3. Reconstruction results and basis coefficients.

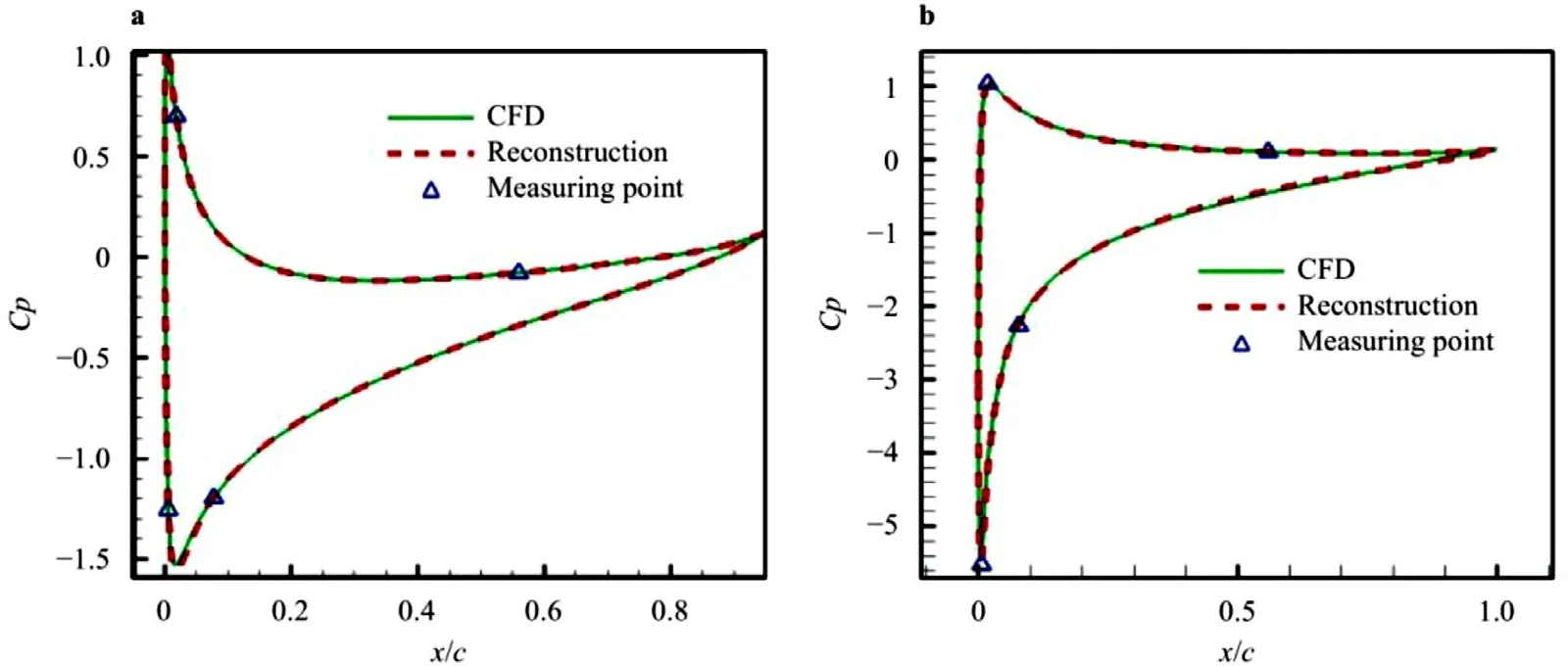
Fig. 4. Reconstruction result. The parameters of the flow field are as follows: a Ma = 0.45, AOA = 4 °, Re = 4.42 ×10 6 ; b Ma = 0.3, AOA = 10 °, Re = 2.95 ×10 6 .

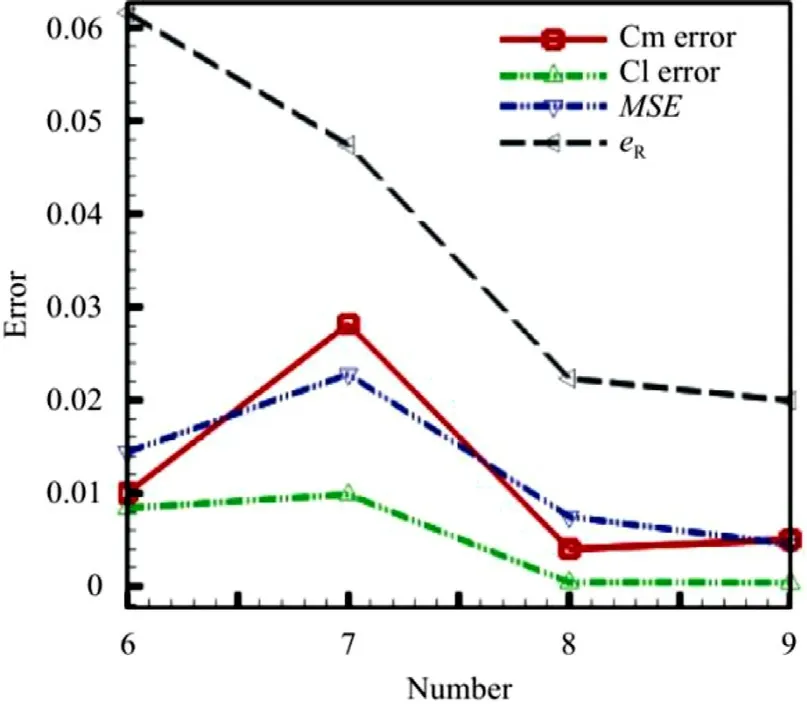
Fig. 5. Influence of increasing the number of measurement points on reconstruction error.

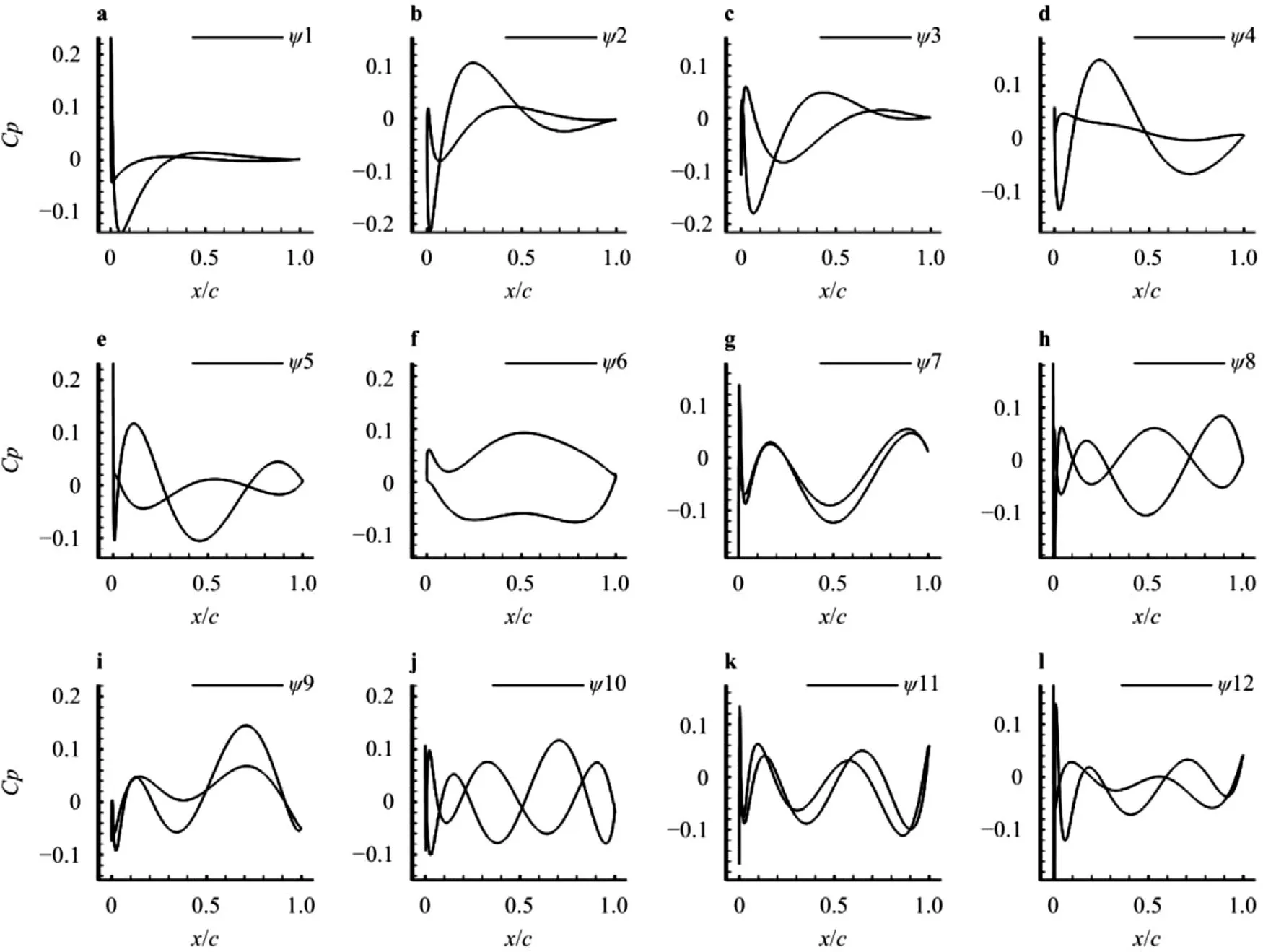
Fig. 6. First 12-order basis functions obtained by POD.

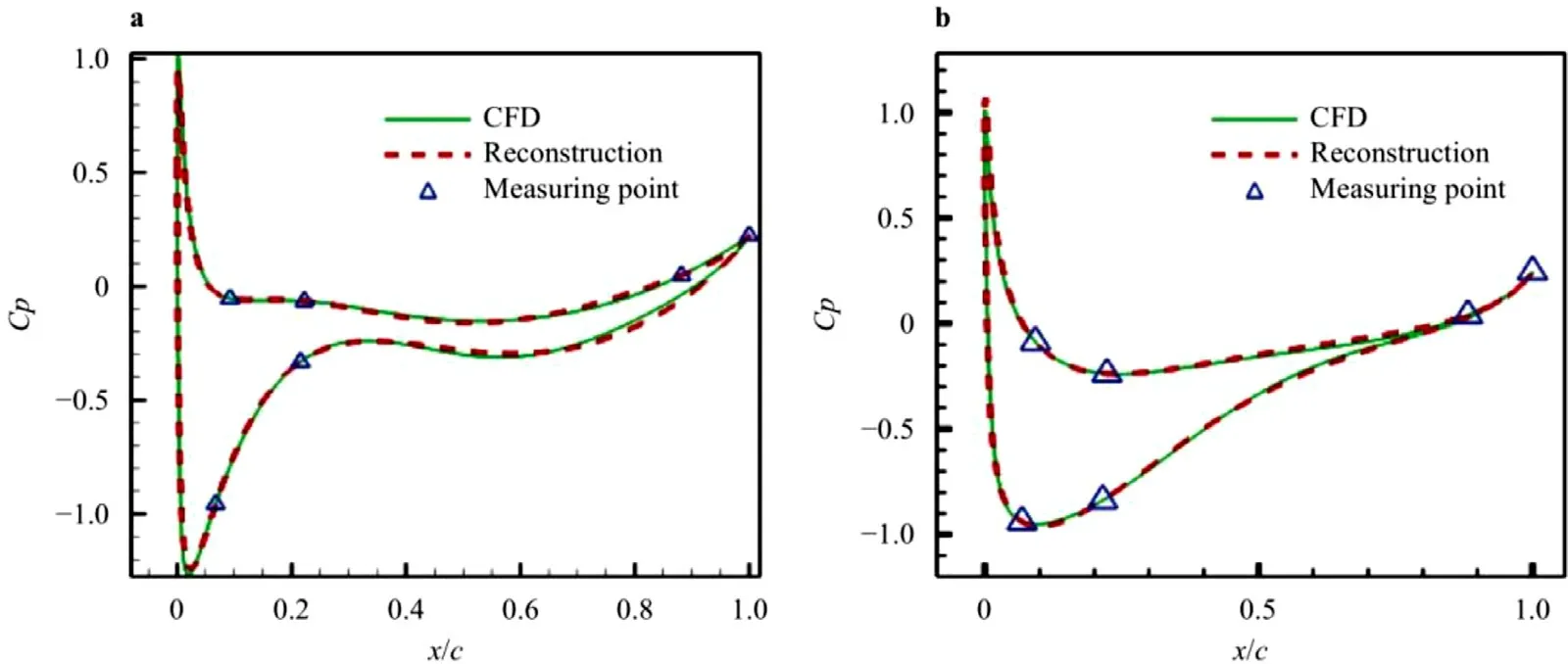
Fig. 7. Reconstruction result of variable airfoil.

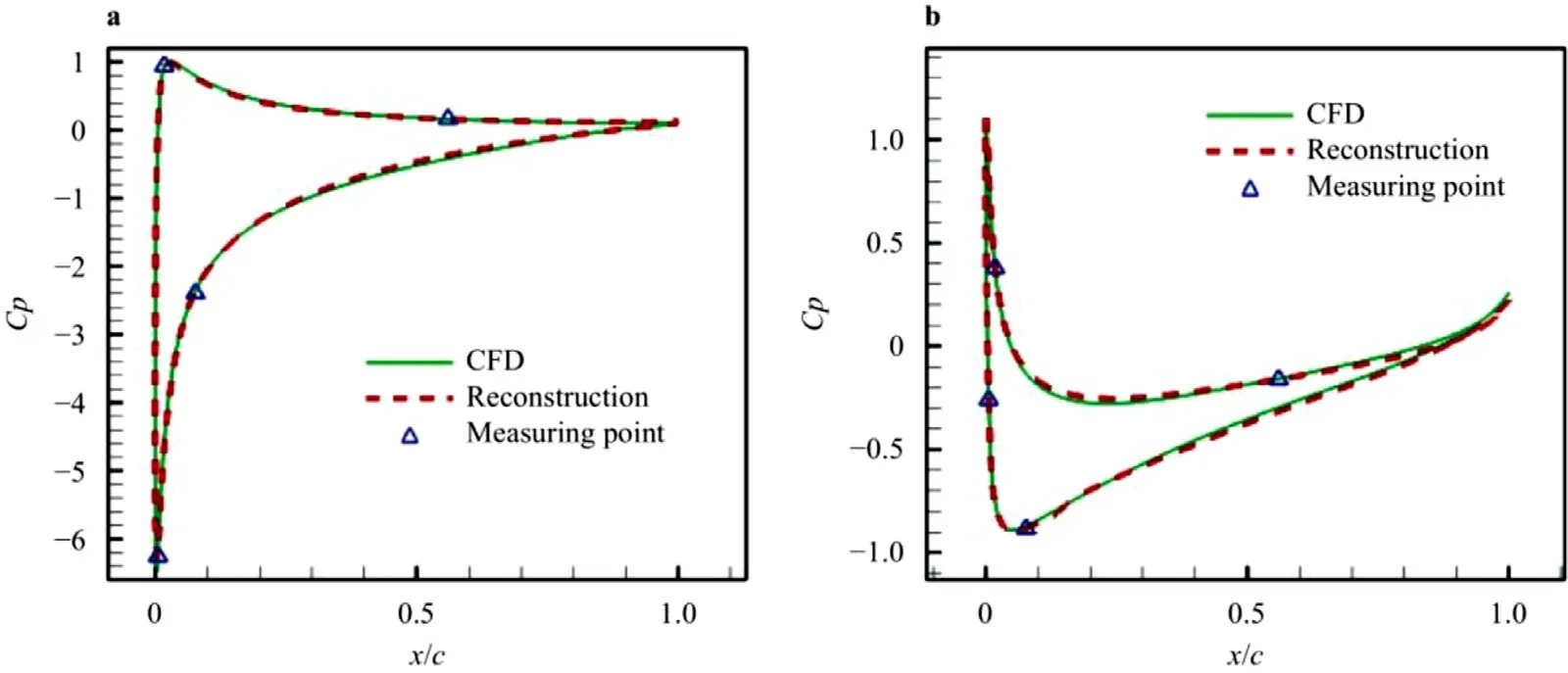
Fig. 8. Reconstruction result after adding noise. The parameters of the flow field are as follows: a Ma = 0.25, AOA = 11 °, Re = 2.46 ×10 6 ; b Ma = 0.55, AOA = 2 °, Re = 5.40 ×10 6 .

In order to quantify the degree of deviation between the reconstructed flow field and the actual flow field, in the paper we define the mean square error (MSE) and relative error (eR ) in Eqs. (5) and(6)

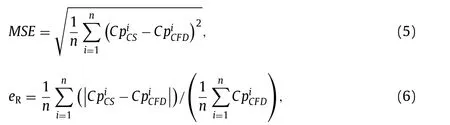
whereis the pressure coefficient reconstructed by compressed sensing,is the pressure coefficient calculated by CFD,nrepresents the number of pressure points on the airfoil surface.

Figure 4 shows the selection of two flow fields in the test set,the measurement point position and weight value are obtained through the PSO algorithm, and the reconstruction results are obtained by compressed sensing algorithm. Table 1 shows the reconstruction error.

Table 1 Comparison of two state errors.

To further improve the reconstruction accuracy, we can increase the number of measurement points, and the position of the measuring point is obtained by the PSO algorithm.

Figure 5 shows the effect of increasing the number of measurement points on the reconstruction error. The red line represents the torque coefficient error (Cm), the green line represents the lift coefficient error (Cl), the blue line representsMSE, and the black line represents the relative erroreR . The error values are statistical value. The results show that 4-8 measurement points are needed,so that the accuracy of the lift and moment coefficients obtained through the reconstructed pressure integral can reach about 0.004,which meets the requirements of the national military standard.

According to the pressure distribution basis function extracted by POD, in order to obtain 99% energy, at least 12 basis functions are needed. Figure 6 shows the obtained sparse basis functions.Here, we reconstruct based on 6 measurement points.

Figure 7 shows the 6 measurement points and 12 weight values corresponding to 12 basis functions obtained by PSO optimization,and the results are reconstructed by the compressed sensing algorithm. The parameters of the flow field are as follows:Ma= 0.3,AOA= 2.5 °,Re= 2.95 ×106. Table 2 shows the reconstruction error of the two states. It can be obtained by comparing the error that the flow field can still be reconstructed with high accuracy based on this algorithm.

Table 2 Comparison of two state errors.

Table 3 Error comparison with noise.

In the second typical calculation example, we calculated 400 sets of pressure distribution data of variable airfoil (300 sets of data as the training set, 100 sets of data as the test set), but did not change the flow field parameters (MaandAOA). The reconstruction results obtained in the test set show that we can still reconstruct the pressure field with high accuracy. Therefore, the algorithm has a certain generalization for airfoil.

Normally, to check the robustness of the algorithm, the test noise should reach 10%-20%, but what is calculated here is the pressure coefficient. When the noise reaches 10% or more, the pressure coefficient fluctuates greatly, which is unrealistic. Therefore, considering the influence of noise in practical engineering applications, it can be known from the literature that the pressure sensors used in the multi-point measurement technology of wind tunnel tests at home and abroad are mostly silicon piezoresistive pressure sensors, which have high sensitivity and are widelyused. At present, the accuracy of pressure sensors used to measure model surface pressure in wind tunnel tests is generally 1%–1.5%.

In the paper, we take 4 measuring points to reconstruct the flow field as an example. The position of the measuring point is obtained by the PSO algorithm, and 1.5% noise is added to the pressure coefficient of the measuring point. Figure 8 shows the result of 1.5% noise addition. The parameters of the flow field are as follows:

In order to make the results more universal, Table 3 compares the reconstruction errors of measuring points with 0%, 1%, and 1.5%noise. The errors are statistical results. It can be known that when 1%–1.5% of noise is added, the pressure field can still be reconstructed well, and this algorithm has strong robustness to noise.

The results obtained in this article are the results of simulation.This paper proposes a refined reconstruction method of airfoil surface pressure based on compressed sensing, which can reconstruct the entire pressure field based on a small number of pressure measurement points. Based on this algorithm, in practical engineering applications, we can reconstruct the pressure distribution of the entire airfoil surface with high accuracy based on the pressure values obtained by a small number of pressure sensors, but the sparse basis function required here may need to be obtained from real experimental data. It provides a new idea for obtaining accurate force data from the sparse surface pressure test in engineering. The main conclusions are as follows.

(1)Based on the compressed sensing algorithm, a strategy of penalizing the high-order basis functions corresponding to the basis coefficients is proposed, which effectively im proves the reconstruction accuracy and robustness.

(2)The measurement point positions obtained by the particle swarm optimization algorithm can effectively improve the reconstruction accuracy under the condition that the number of measurement points remains unchanged.

(3)Through the NACA0012 calculation example, the results show that 4-8 measurement points are needed, so that the accuracy of the lift and moment coefficients obtained through the reconstructed pressure integral can reach about 0.004, which meets the requirements of the national military standard. And by introducing measurement noise, it is verified that the method is also robust against noise.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

This work was supported by the foundation of National Key Laboratory of Science and Technology on Aerodynamic Design and Research (Grant 614220119040101), the National Natural Science Foundation of China (Grants 91852115 and 12072282), the National Numerical Wind tunnel Project (Grant NNW2018-ZT1B01), and the Seed Foundation of Innovation and Creation for Graduate Student in Northwestern Polytechnical University (Grant CX2020195).