Bifurcation mechanism of interfacial electrohydrodynamic gravity-capillary waves near the minimum phase speed under a horizontal electric field

Gexing Xu, Zhi Lin

School of Mathematical Sciences, Zhejiang University, Zhejiang 310027, China

Keywords: Solitary waves Bifurcation mechanism Horizontal electric field Kelvin–Helmholtz instability

A B S T R A C T We investigate the evolution of interfacial gravity-capillary waves propagating along the interface between two dielectric fluids under the action of a horizontal electric field. There is a uniform background flow in each layer, and the relative motion tends to induce Kelvin–Helmholtz (KH) instability. The combined effects of gravity, surface tension and electrically induced forces are all taken into account. Under the short-wave assumption, the expansion and truncation method of Dirichlet-Neumann (DN) operators is applied to derive a reduced dynamical model. When KH instability is suppressed linearly by a considerably large electric field, our numerical results reveal that in certain regions of parameter space, nonlinear symmetric traveling wave solutions can be found near the minimum phase speed. Additionally, the detailed bifurcation structures are presented together with typical wave profiles.

Electrohydrodynamics (EHD), a subject dealing with the interplay of fluids with electric fields, has a wide range of applications in industry, chemistry and biology, such as industrial coating process, electrospray ionization and biological membranes, etc. [1–3] .Due to practical purposes, in-depth investigations about the wave formation and the bifurcation of EHD interfacial waves are necessary. It is well known that the effect of electric fields can be stabilizing or destabilizing, broadly depending on its orientation relative to the unperturbed interface. A typical work conducted by Taylor and Melcher [4] verified theoretically and experimentally that the vertical field can destabilize the interface between conducting and non-conducting fluids. On the contrary, the horizontal field has a dispersive stabilization to the interface, and can be employed to suppress the Rayleigh–Taylor (RT) and Kelvin–Helmholtz (KH) instabilities [ 5 , 6 ].

Recently, the research of EHD has made a huge progress. There is a plethora of mathematical models proposed in terms of different physical backgrounds. Easwaran [7] derived first a Kortewegde Vries (KdV) for the motion of long waves on a conducting fluid layer under the influence of a vertical electric field, and its corresponding coefficients are related to the applied electric field. In the perfect dielectric fluid influenced by a horizontal field, Tilley et al. [8] derived an evolution equation including a Hilbert transform which is a nonlocal operator, and further showed the stabilizing effect of the electric field which can delay the formation of rupture.Papageorgiou [9] summarized systematically long-wave theories on film flows in the review paper. These studies were all based on the long-wave model. However, in present problem we derive a reduced short-wave model for gravity-capillary (GC) waves between two semi-infinite dielectric fluids.

When the electric field is absent, the research of interfacial GC waves has been investigated by many scholars over the past few decades. It is noted that there are two conditions proposed by Akylas [10] for the existence of wavepacket solitary waves. The first one is the phase speed has a global extrema at the finite wavenumber. The other is that the associated nonlinear Schrödinger (NLS) equation is of foucsing type. However, in the interfacial water waves problem, Laget and Dias [11] found wavepacket solitary waves that only exist with the finite amplitude by using the direct numerical simulation method to the full Euler equations when the NLS equation is defocusing (i.e., the second condition is not satisfied). On the side of the bifurcation theory, Wang et al. [12] proposed a dynamical model to further explain their bifurcation mechanism for finite-amplitude solitary waves. However, if a uniform background flow is introduced in each layer resulting in a velocity jump across the interface, Wessiman [13] showed that wavepacket solitaty waves also exist in linearly stable region, but it is susceptible to KH instability.

In this paper, introducing two additional physical effects of the uniform background flow and the horizontal electric field, we consider interfacial GC waves propagating along the interface between two semi-infinite dielectric fluids. For the electrocaplliary waves,Grandison et al. [14] found that the horizontal electric field can linearly stabilize symmetric and antisymmetric modes supporting a tangential velocity discontinuity at the interface when the strength of the applied electric field is greater than a threshold required to suppress KH instability. In the nonlinear instability of KH problem for two dielectric fluids, Elhefnawy [15] showed that in the linearly stable regime the cubic NLS equation is an appropriate governing equation describing the amplitude of wavepackets under the action of an oblique electric field. Based on the argument above, we confine our attention in the linearly stable region to search for symmetric traveling wave solutions predicted by the cubic NLS equation in certain regions of parameter space where KH instability is suppressed by the applied electric field.

Consider two immiscible, inviscid and incompressible dielectric fluid layers of infinite depth in the two-dimensional setting, with the lighter fluid lying atop the heavier one, influenced by a uniform horizontal electric field. In the undisturbed state withy= 0 ,the flows are supposed to be irrotational, and the upper layer (superscripts + ) and the lower layer (superscripts –) both have a horizontal uniform flow, a constant density and an electrical permittivity, denoted byU±,ρ±andε±, respectively. When the flows are perturbed infinitesimally, the interface can be describedy=η(x,t),wherex-direction is parallel with uniform flows andyis the vertical coordinate. If the electric field in each layer is denoted byE+andE−, they satisfy both ∇E±= 0 due to the electrostatic limit of Maxwell equations, and hence we can introduce voltage potentialsV±. Under this setup, the perturbed flows must be irrotational in each half-layer due to the motion developing from an irrotational basic state. Hence velocity potentialsΦ±and voltage potentialsV±satisfy Laplace equation

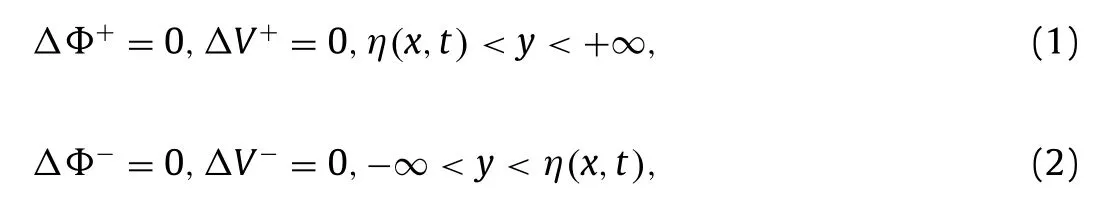
whereΔ=∂xx+∂yy. The total velocity potentialsΦ±can be decomposed into background plus perturbations

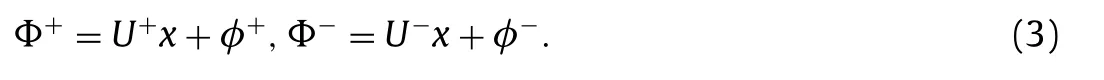
It is obvious that perturbationsφ±must satisfy also Laplace equation. At the interfacey=η(x,t), the kinematic and dynamic conditions

whereσis the coefficient of surface tension, n =is the unit normal vector at interface, pointing upwards from the lower-layer fluid, andarises from the Maxwell’s stress tensor {Σij}i,j=1,2 given by

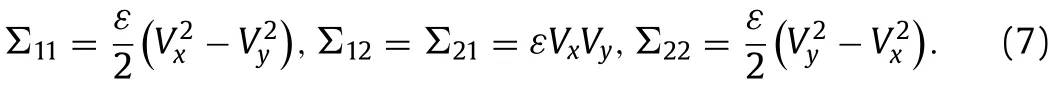
A tedious but straightforward calculation shows that

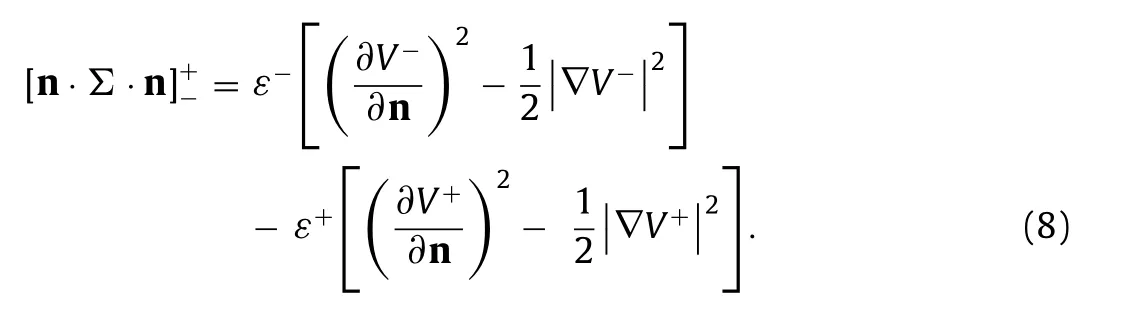
In addition, there are two boundary conditions which voltage potentials have to satisfy at the interface, namely, the continuity of voltage potentials and the discontinuity of their normal derivatives

As far away from the interfacial disturbances, the condition for voltage potentials should be imposed by

For the sake of simplicity, we introduce modified voltage potentials by

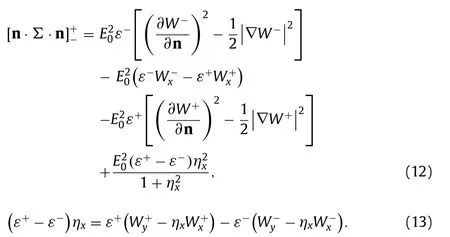
Taking into account gravity and surface tension, we choose[σ/(ρ−g)]1/2 , [σ/(ρ−g3)]1/4 andσ3/[(ρ−)3g]1/4 as length, time,potential scales respectively, and define the dimensionless parametersandε=ε−/ε+, hence the dynamic boundary condition can be recast into the dimensionless form

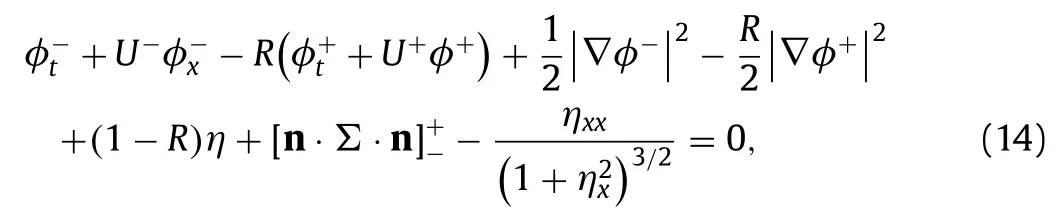
with

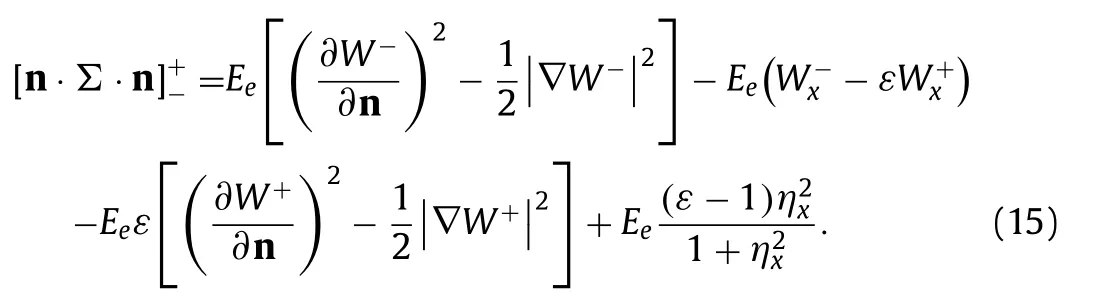
Eventually, the boundary conditions±∞ ) constitute the two-fluid system.

We linearize the whole system by dropping nonlinear terms in Eqs. (4) , ( 5 ), ( 13 ) and ( 14 ), and apply the method of normal modes to get the phase speed ofas below

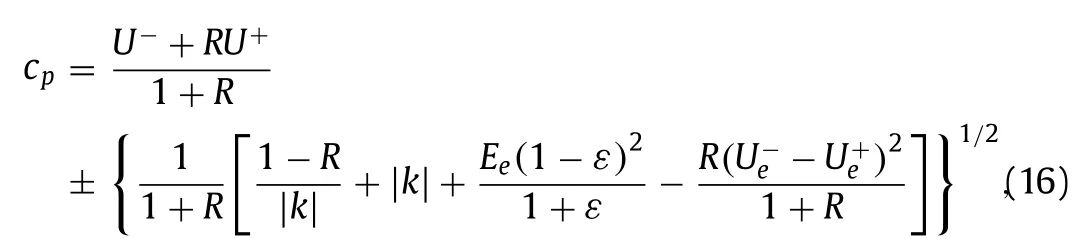
where two phase speeds have both global extrema atIn subsequent analysis, we mainly consider the branch of largercpsince it is likely subject to KH instability. The critical velocity difference that destabilize the system is

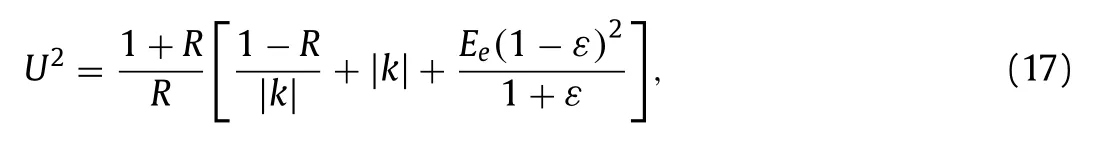
Throughout the paper, we mainly focus on the effect of the applied electric field on the system. As shown in Fig. 1 by fixed parameters:R= 0.4 ,ε= 0.2 , it illustrates the applied electric field can suppress KH instability since there is a greater velocity difference compared the case where the applied electric field is absent.In the subsequent numerical experiment, the analysis provides a guid for us to select the value of velocity differenceUin(1a,1b).

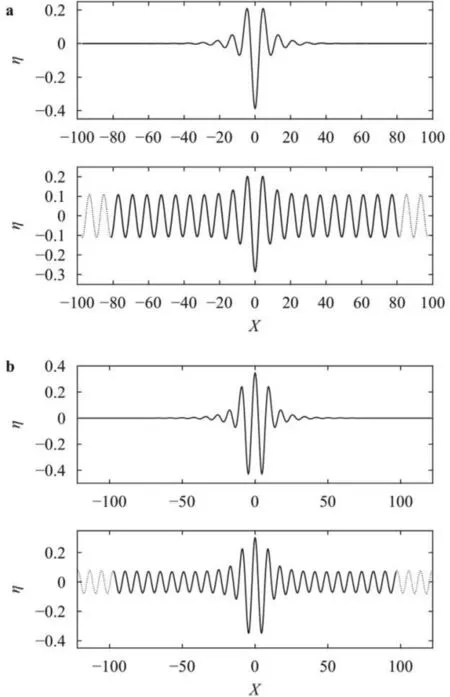
Fig. 2. Examples of bright and generalized solitary waves. a The top shows the depression of bright solitary waves with c = 1 . 986 , and the bottom shows the depression of generalized solitary waves with c = 1 . 991 , using different com putational domains of 40 π/ k c (dotted line) and 48 π/ k c (solid line). b The top shows the elevation of bright solitary waves with c = 1 . 988 , and the bottom shows the elevation of generalized solitary waves with c = 1 . 9905 , using different com putational domains of 48 π/ k c (dotted line) and 60 π/ k c (solid line).

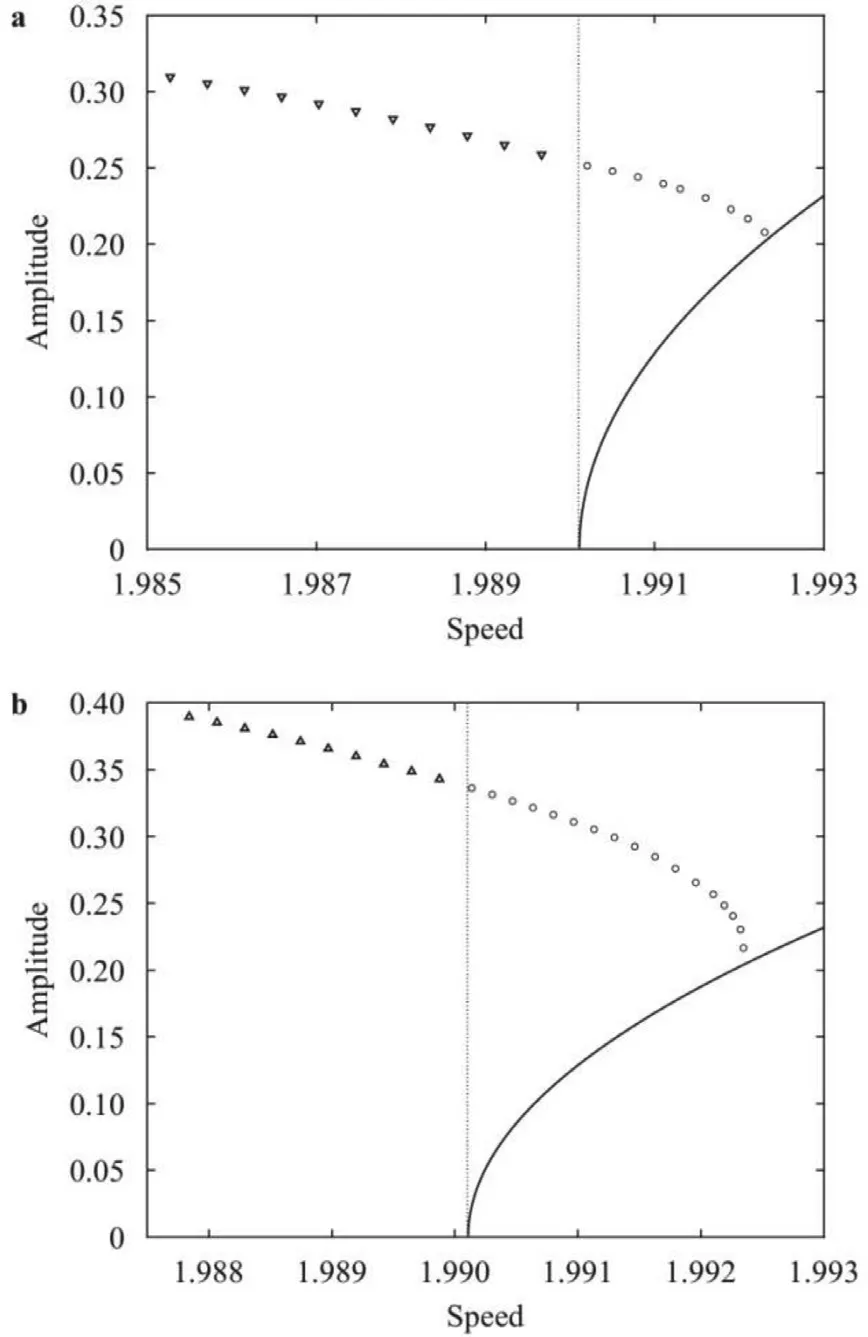
Fig. 3. Speed-amplitude diagrams for the depression and elevation branch, corresponding to the panel a and b . The circles show the generalized solitary waves, and the triangles pointing downward and upward indicate the bright depression and elevation solitary waves, respectively. The amplitude parameter in all cases presented is [ max (η) −min (η) ] / 2 .

Fig. 4. a Speed-amplitude diagram (solid line) for the depression dark soliton branch with the concave-up middle phase near c min ≈1 . 9901 , and the amplitude parameter is [max (η) −min (η) ]/2. b Typical wave profiles as the amplitude increases respectively correspond to points 4 a -4 d marked in the left plot using the different computational domains 51 π/ k c (dash line) and 63 π/ k c (solid line), and the NLS prediction is shown (dash-dot line).

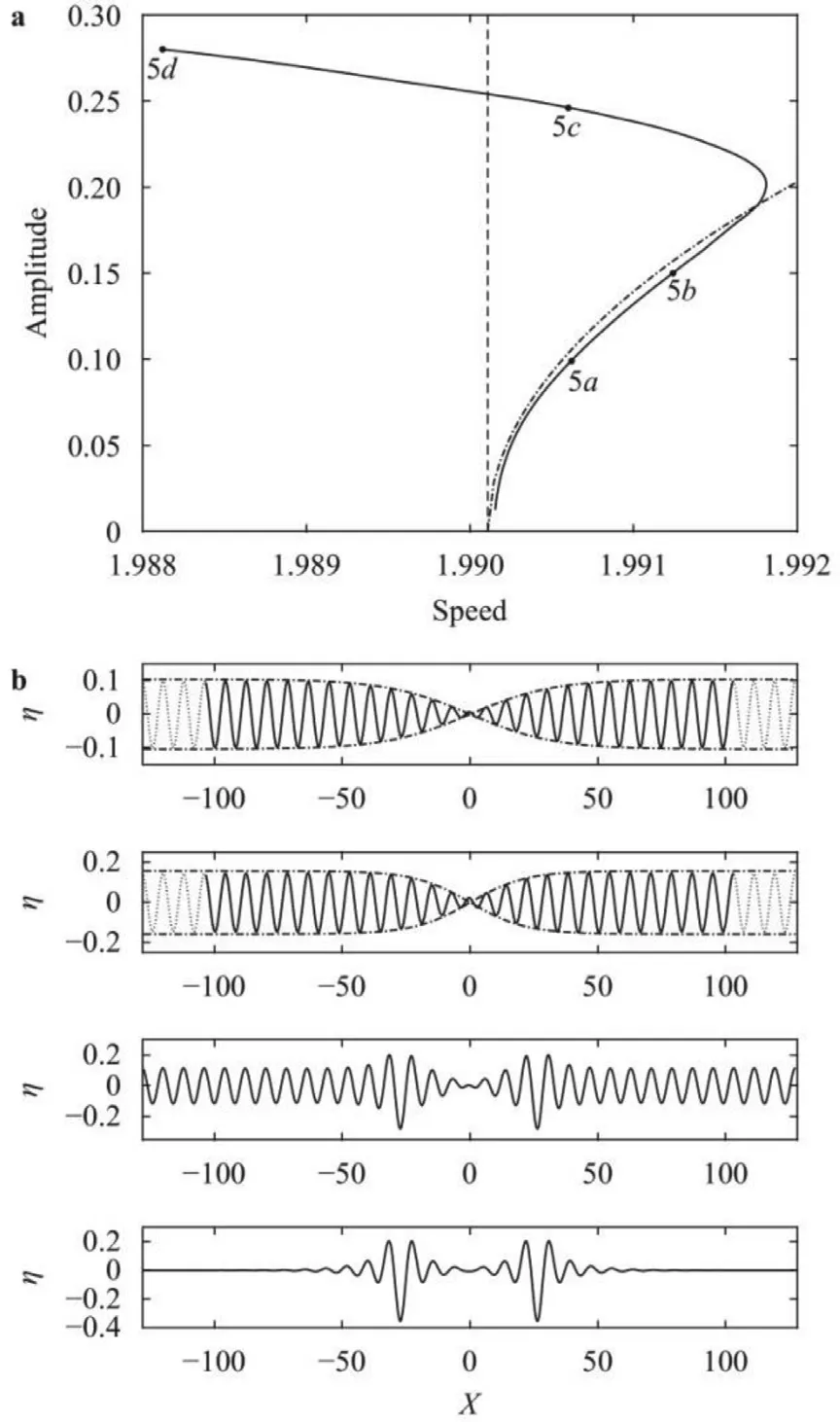
Fig. 5. a Speed-amplitude diagram (solid line) for the elevation dark soliton branch with the concave-up middle phase near c min ≈1 . 9901 , and the amplitude parameter [ max (η) −min (η) ] / 2 . b Typical wave profiles as the amplitude increases respectively correspond to points 5 a -5 d marked in the left plot using the different com putational domains 51 π/ k c (dash line) and 63 π/ k c (solid line), and the NLS prediction is shown (dash-dot line).

We introduce Dirichlet-Neumann (DN) operators to avoid solving the Laplace equation and use DN operators expansion to derive the evolution equation. If we denote velocity potentials and modified electric potentials across the interface asξ±=φ±(x,η(x,t),t)andW(x,t)=W±(x,η(x,t),t)respectively, and define DN operatorsG±(η)in the following

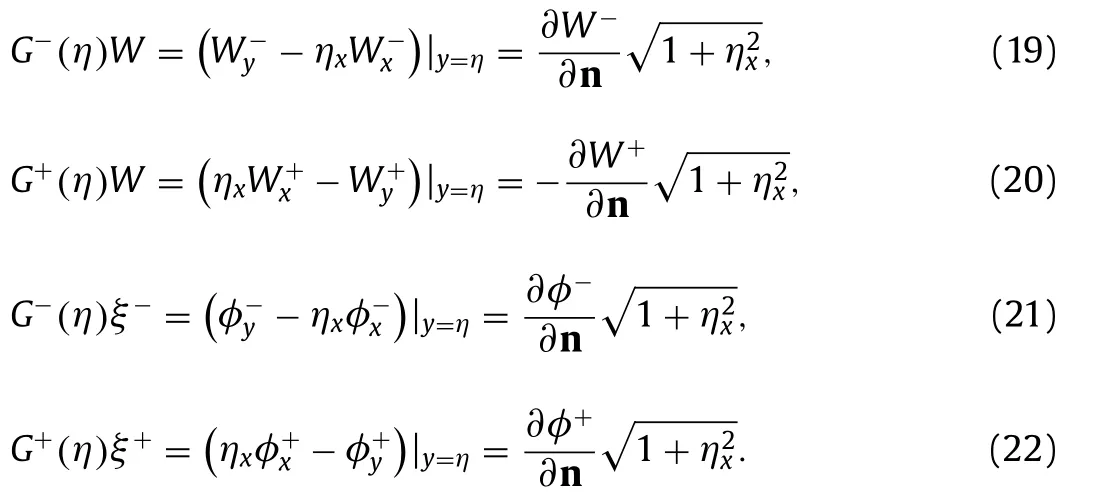
Following Benjamin and Bridges [16] , we introduceξ=ξ−−Rξ+, and in terms of Eqs. (19) and ( 20 ), it follows that

Hence we can recast the boundary conditions at the interface in terms ofξ,ηand DN operators

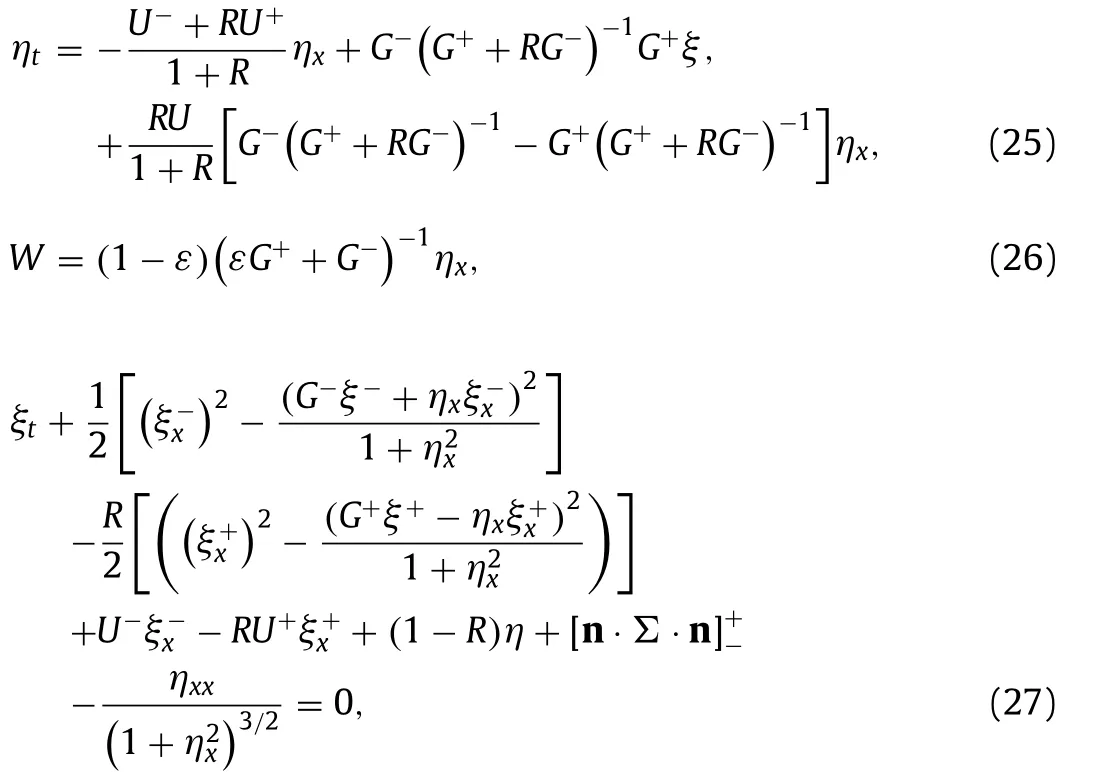
where

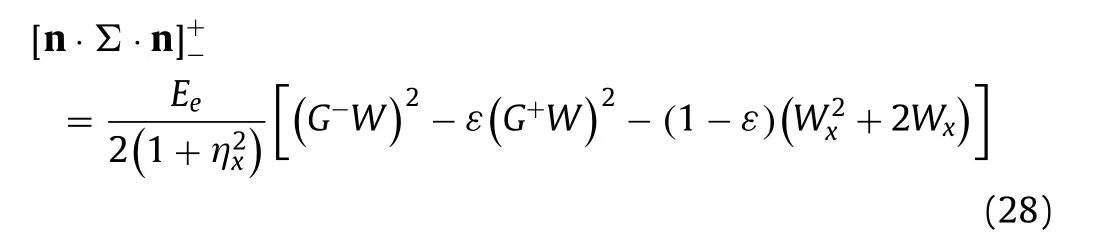
Following Craig et al. [17] and Wang [18] , it follows that DN operators can expand as Taylor seriesandif theC1-norm ofηis smaller than a certain constant. The first three terms of Taylor series of DN operators are given as

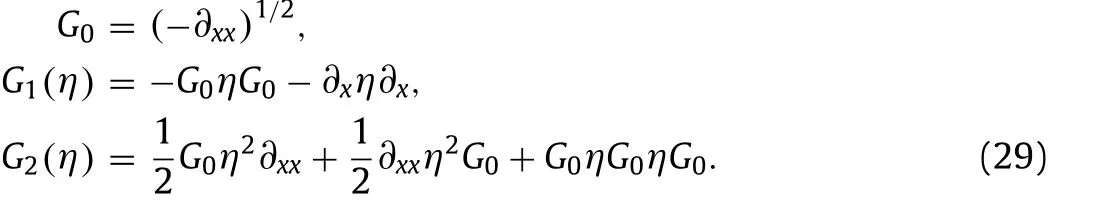
We assume thatξandηare all of orderO(∊)in subsequent analysis and then set about deriving a cubic reduced model by expandingG±and truncating terms higher thanO(∊3)in Eqs. (25) –( 27 ). After lengthy but straightforward calculation, one obtains a reduced quantitative model system for EHD interfacial GC waves in deep water

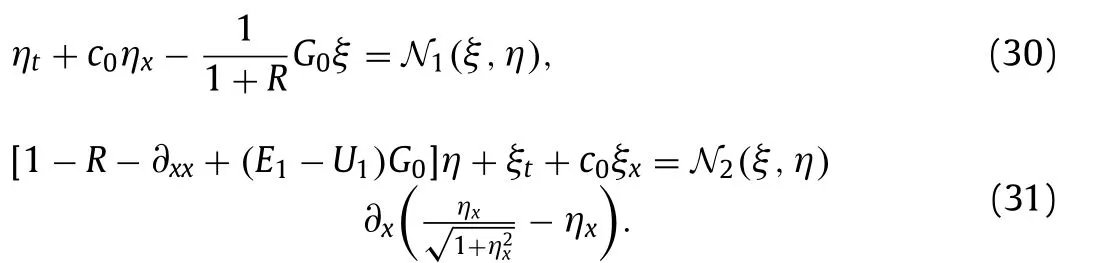
with

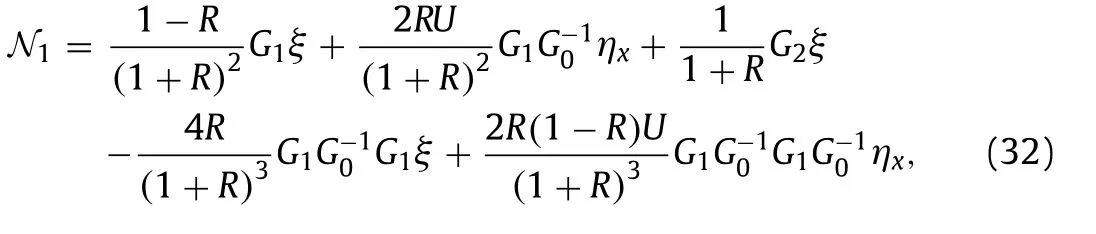
NLS equation provides a good prediction for wavepacket solitary waves. In the spirit of Dias and Iooss [19] , we introduceX=∊x,T=∊t,τ=∊2tand pick e i(kx−wt)as the carrying wave. For brevity of the derivation, it is useful to point out the following formulae

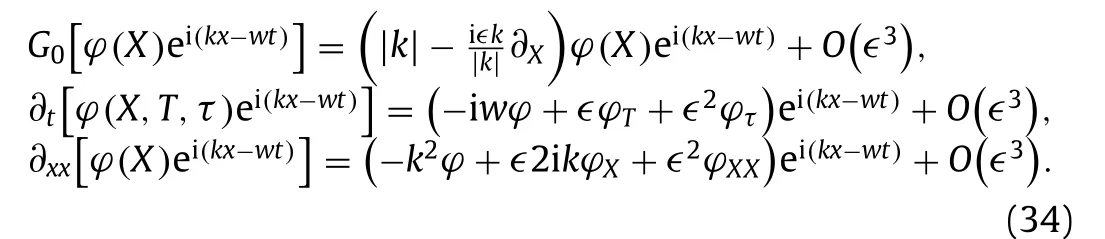
We can obtain NLS by substituting the following ansatz

into the evolution system of Eqs. (30) and ( 31 ), and equate like powers of∊. It is noted thatAjandBjinclude all the harmonic modes, namely,and so doesBj. First of all, the leading order termsO(∊)result in the equations

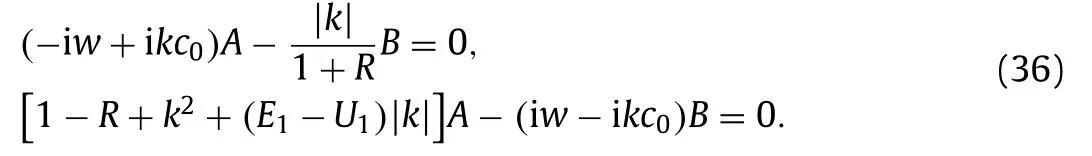
The nonzero solution implies the dispersion relation and the relation betweenAandB

where

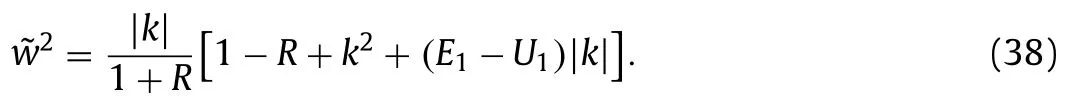
The terms of orderO(∊2)give the equations forA1andB1.The corresponding linear system is also degenerate because of the dispersion relation. The solvability condition for ei(kx−wt)indicates thatAhas an implicit dependence onT(i.e.,A(X−cgT,Y,τ)) and so doesB, whereis called the group velocity

Finally the solvability condition of the mode ei(kx−wt)forO(∊3)gives the cubic NLS equation

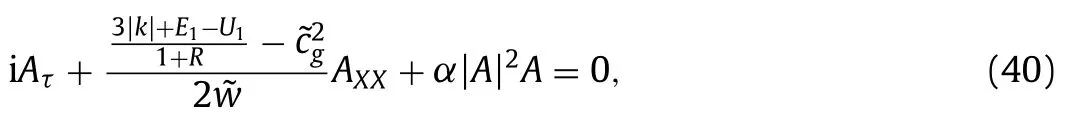
whereand

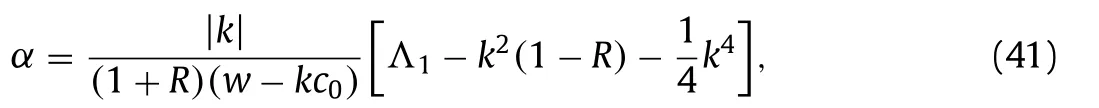
with

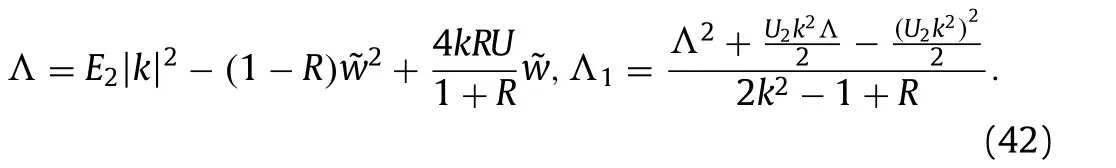
Since the group velocity coincides with the phase velocity at the minimum phase speed, the wavepacket solitary waves may bifurcate from the free stream at the point as long as the associated NLS is of focusing type. In what follows, we confine ourselves to investigate the NLS coefficients at the minimum point.Atthe minimum isand the corresponding NLS reads

with

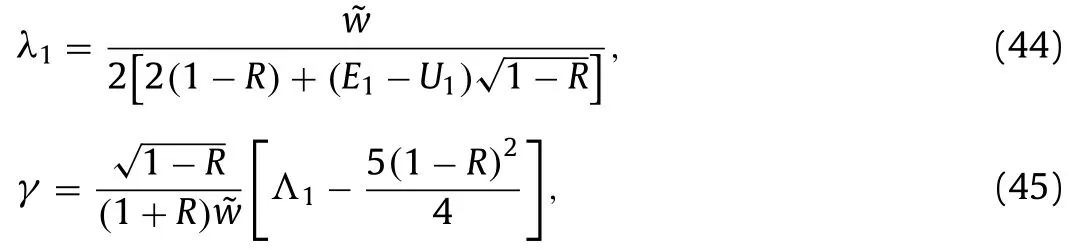
where

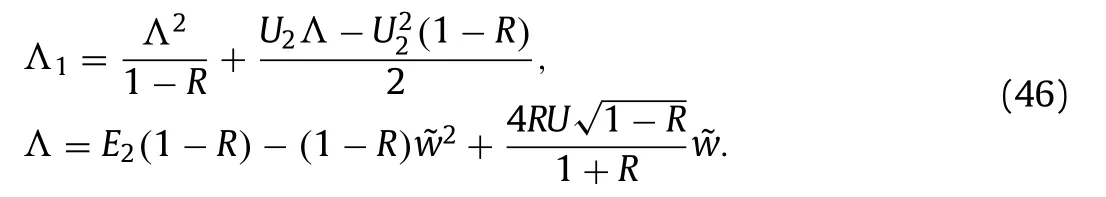
It is seen from Eqs. (38) and (4 4) thatis positive definite atin the linearly stable regime whereU0 . Therefore, the nonlinear coefficientγin Eq. (43) is the only term determing the type of the associated cubic NLS equation. Asγ>0 , the cubic NLS equation is foucsing and admits a sech -type bright soliton solution. The other case,γ<0 ,it is defocusing and predicts a tanh -type dark soliton solution. In this paper, we are of primary concern for the latter case.

For the sake of brevity, we first transform the system ( 31 ) into a single evolution equation in Fourier space by introducing

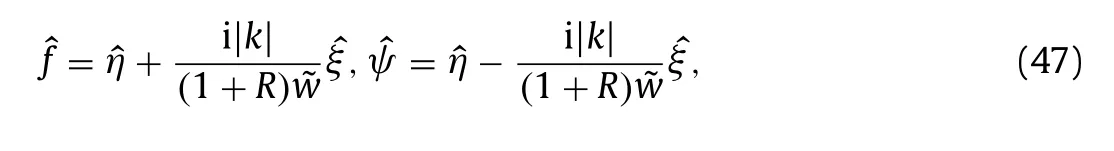
and hence the system can be rewritten as follows

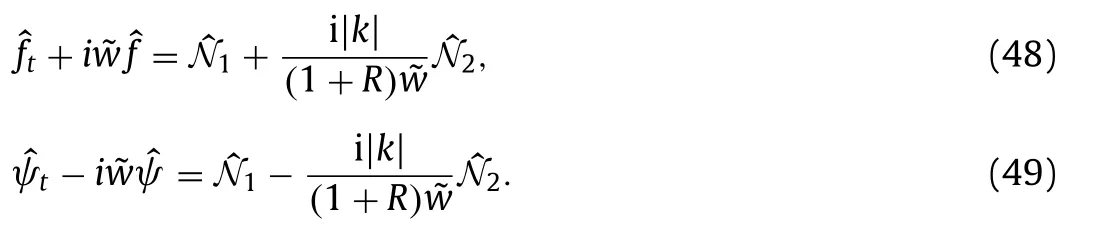
Equations (48) and ( 49 ) are essentially equivalent sinceξandηare real. Moreover,ηandξcan be recovered

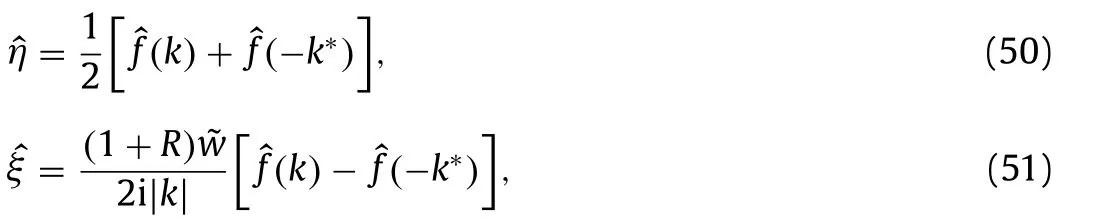
where the asterisks imply the complex conjugate. In order to compute traveling solutions, Eq. (48) can be numerically solved using a pseudo-spectral method and Newton iterations, with an initial guess obtained by the vanishing pressure method [20] . To simply the prblem, we only compute the symmetric traveling wave solutions.

We search for traveling wave based on the quantitative model under a given set of parameters:Ee= 5 ,ε= 0.2 ,R= 0.4 . Substituting the three values into Eq. (18) , we can obtain that two critical velocity differences are 2.326 , 3.8413 , respectively corresponding toE= 0 andE= 5 . Hence we choose an appropriate velocity difference at the interfaceU= 3 ∈(2.326,3.8413)for example. The coefficients of the associated cubic NLS equation in Eq. (43) become

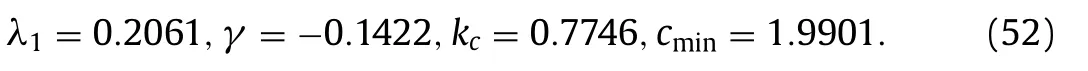
It is seen that the associated NLS equation is of defocusing type forγ<0 .

It is well known that the defocusing NLS equation excludes the small-amplitude solitary waves, but finite-amplitude solitary waves also can be found [ 11 , 12 ]. Next, we use the numerical scheme to search for such solutions based on a quantitative reduced model.As shown in Fig. 2 , there are two kinds of finite-amplitude bright solitary waves in the system, namely, the depression and elevation solitary waves. The corresponding local bifurcation curves nearcminare illustratedin Fig. 3 . Take the depression branch for example, shown in Fig. 3 a. Following the curve by increasingc, we see that oncecexceedscmin, the finite-amplitude solitary waves will resonate with periodic waves (i.e., Stokes waves) resulting in the generalized solitary waves characterized by a localized midsection and non-decaying oscillatory tails. Further increasingc, the branch of generalized solitary waves are incorporated into the branch of periodic waves. In addition, we compute the generalized solitary waves with different domain sizes ( 40 π/kcand 48 π/kcfor the depression branch, 48 π/kcand 60 π/kcfor the elevation branch). It is seen from Fig. 2 that the profile computed in the larger domain is basically superposed the one with the smaller domain, only the periodic tails being added in the far field. The fact strongly implies the existence of real generalized solitary waves when domain size tends toward infinity. The bifurcation mechanism for the elevation branch is similar.

In the following, we consider dark solitary waves which are predicted by the defocusing NLS equation. In order to avoid Stokes wave, a numerical trick documented in Ref. [21] suggests that we need to select a domain with size(2n+ 1)π/kcforn= 22,23,···,37 . We found the depression and elevation branch shown in Figs. 4 and 5 for dark solitary waves. The typical profiles,featuring the concave-down and concave-up middle phase respectively, are presented in Figs. 4 b and 5 b along the corresponding bifurcation curve respectively. Taking the depression branch for example shown in Fig. 4 , it is seen that the dark solitary waves bifurcate from infinitesimal periodic waves. Along the bifurcation curve by increasing the amplitude, the bifurcation curve shows a turning pointc≈1.9918 . Further increasing the amplitude, the corresponding waves evolve into multi-pulse generalized solitary waves, and finally develop into the multi-pulse bright solitary waves as passing through the bifurcation pointcminfrom its right to left. This bifurcation mechanism for the elevation branch is analogous.

In this paper, for interfacial gravity-capillary waves, we proposed a quantitative reduced model via expanding and truncating DN operators in the full Euler equations when the physcial effects of gravity, surface tension, a horizontal field, a uniform flow were all taken into account. Moreover, we performed a linear stability analysis to clearly show the surface tension and the horizontal electric field provide a linearly dispersive stabilization to the system and to show the identification of parameter regime where the applied electric field can suppress linearly KH instability. In terms of the analysis, we used the pseudo-spectral method and Newton iterations to solve the proposed model and found symmetric traveling wave solutions at the linearly stable region. Additional,we further presented their the bifurcation structure in the vicinity of the minimum phase speed. It is also worth mentioning that the stability and dynamic properties of computed traveling waves merit further study in the future.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant 12071429 ).