A model for universal spatial variations of temperature fluctuations in turbulent Rayleigh-Bénard convection

Xiaozhou He , Eberhard Bodenschatz , Guenter Ahlers

a School of Mechanical Engineering and Automation, Harbin Institute of Technology, Shenzhen 518055, China

b Max Planck Institute for Dynamics and Self Organization, D-37073 Göttingen, Germany

c International Collaboration for Turbulence Research

d Institute for Nonlinear Dynamics, University of Göttingen, D-37073 Göttingen, Germany

e Laboratory of Atomic and Solid-State Physics and Sibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, NY 14853, USA

f Department of Physics, University of California, Santa Barbara, CA 93106, USA

Keywords: Rayleigh-Bénard convection Temperature variance profile Attached-eddy Law of wall

A B S T R A C T We propose a theoretical model for spatial variations of the temperature variance σ2 ( z, r ) ( z is the distance from the sample bottom and r the radial coordinate) in turbulent Rayleigh-Bénard convection (RBC).Adapting the “attached-eddy”model of shear flow to the plumes of RBC,we derived an equation forσ2 which is based on the universal scaling of the normalized RBC temperature spectra. This equation includes both logarithmic and power-law dependences on z/ λth , where λth is the thermal boundary layer thickness. The equation parameters depend on r and the Prandtl number Pr , but have only an extremely weak dependence on the Rayleigh number Ra Thus our model provides a near-universal equation for the temperature variance profile in turbulent RBC.

Rayleigh-Bénard convection (RBC) is the flow of fluid confined between two horizontal plates and heated from below in the presence of gravity [1–4] . For a closed sample, the RBC flow is uniquely determined by the Rayleigh numberRa≡αgΔL3/(νκ), the Prandtl numberPr≡ν/κ, and the aspect ratio of the sample. Heregis the gravitational acceleration,Δis the temperature difference between the horizontal plates,Lis the sample height, andα,ν, andκare,respectively, the thermal expansion coefficient, the kinematic viscosity, and the thermal diffusivity of the fluid.

We present a model for the temperature-variance profileσ2(z,r)= 〈ΔT2〉/Δ2in turbulent RBC at a fixed lateral positionras a function of the distancezfrom the top or bottom plate. Here 〈...〉 represents the average over the timet,ΔT2=〈 [T(z,r,t)−〈T(z,r,t)〉 ]2〉 whereT(z,r,t)is the local instantaneous temperature, andΔis the applied temperature difference. In what follows we shall, for simplicity, omit the explicit indication thatσ2(z)=σ2(z,r)depends onr. To a large extent our arguments are similar to those of Perry et al. [5] for velocity fluctuations in shearflow wall turbulence, with the “attached-eddy”excitations of shear flow [6] replaced by the plumes emitted from the top and bottom boundary layers (BLs) of turbulent RBC. Thus we expect our model to have validity at values ofrwhere plumes are rising and falling,which (for a cylindrical sample) is expected to be at radial positions not too close to the vertical centerline.

Our model assumes that there are “inner layers”near the horizontal plates where the thermal plumes at a distancezfrom a plate are attached to the plate and thus have the characteristic length scalez. Further away from the plate but in the region where the temperature has a logarithmic profile, the plumes are detached from the plate and their scale is taken to be constant and equal toZ0. This size corresponds to the upper limit of the “inner-layer”size. In this region and for wave numbersknot too large the temperature spectraΦ(k)are characterized by the scales ofΔ, the distance from the platez, andFor very largekthe spectrum is governed by the thermal diffusivity. We choseΔas the RBC temperature scale for it represents the largest temperature difference applied to the system and it generates all the internal temperature fluctuations.

The spectrumΦ(k)has several regions as illustrated in Fig. 1 ,and (according to Parseval’s theorem) its integral over the whole range ofkis equal toΔT2. In the figure, the constantF(which is representative of the outer layer) represents the large-scale contribution to the variance and is expected to be comparable to the RBC sample size. The other constantsH,GandSat the boundaries of the other spectral regions represent near-plate contributions on various scales. They are expected to be universal whenRais suffi-ciently large.

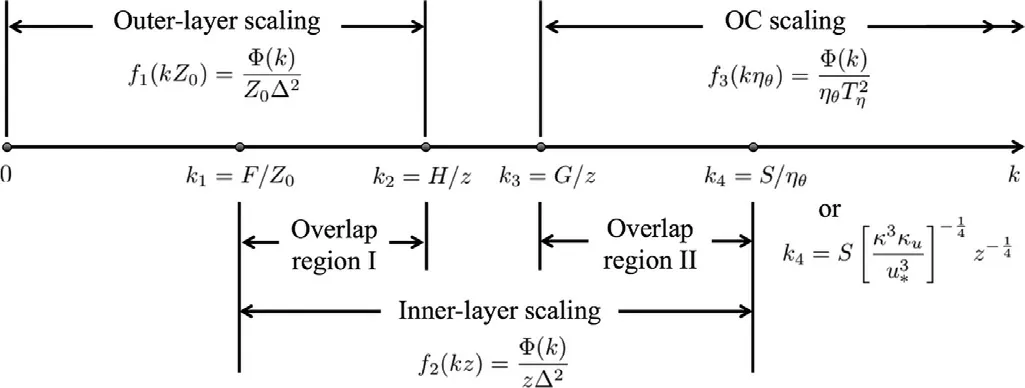
Fig. 1. Schematic diagram of the various temperature spectral regions in RBC.

In the small-wave-number region, the contribution toΦ(k)comes from large plumes with a size of order. The spectrum is determined byZ0 and the temperature scaleΔ, and on the basis of dimensional analysis its dimensionless form can be written as

This form is referred to as the “outer-layer”scaling.

In the moderate-wave-number region, the main contribution to temperature fluctuations comes from the “attached plumes”with a size of orderz. The dimensionless spectral formf2(kz)then has the “inner-layer”scaling

Previous research showed that the temperature near the horizontal plate but away from the BL behaves like a passive scalar [7] .The small-scale temperature fluctuations, which correspond to the high-wave-number region ofΦ(k), were predicted to be governed by the thermal dissipation rate∊T(z,r)≡κ〈(∇T(z,r,t))2〉t, the viscous dissipation rate∊u(z,r)≡ν〈(∇V(z,r,t))2〉t, and the thermal diffusivityκ[ 8 , 9 ] (νis the kinematic viscosity andV(z,r,t)is the local flow velocity). In this case the corresponding length scaleηθand temperature scaleare given by

As a result, the temperature spectrum for the large-kregion has the dimensionless form

We derived expressions forηθandas follows. For the near-wall velocity, it was assumed that the turbulent energy production rate and viscous dissipation rate are approximately in balance [6] . Then one has

whereuandware, respectively, the velocities along and perpendicular to the flow stream-wise direction. In the plume dominated region of RBC, we assume that the temperature fluctuations in the log layer follow the similar balance

The two time-averaged derivatives can be calculated from the “Law of the Wall”for both velocity and temperature profiles. This yields

and the temperature scale

for small-scale fluctuations.

As shown in Fig. 1 , there are two overlap regions in the wavenumber domain. In overlap region I, both the outer-layer scaling and the inner-layer scaling are expected to be valid, and one has

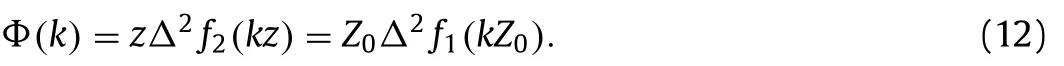
The only solutions to Eq. (12) in overlap region I are

Similarly in overlap region II, both the inner-layer and the highwave-number spectral form are simultaneously valid, which gives rise to

This overlap region is also known as the inertial subrange, in which a passive temperature spectrum is expected to have the Obukhov-Corrsin (OC) scaling [ 8 , 9 ]

whereC0 is an integration constant. From Eqs. (10) , (11) and (16) ,one finds

for overlap region II.

According to Parseval’s theorem, one has the temperature varianceThis integration can be split into several regions as discussed above, which gives

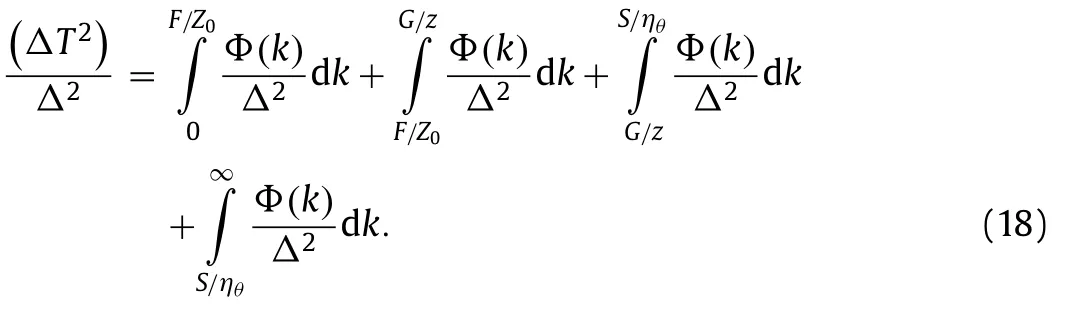
The first term in Eq. (18) comes from the large-scale contribution,which equals a constant determined by the flow. The second term comes from the inner-layer contribution, which can be calculated using Eqs. (2) and (14) :

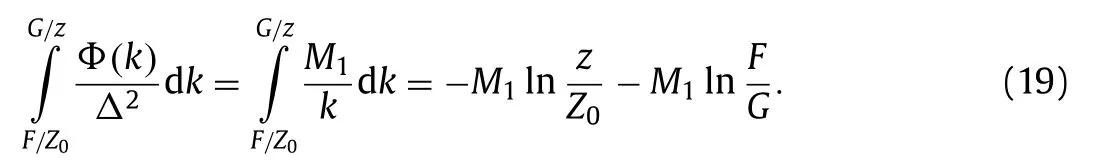
The third term in Eq. (18) represents contributions from the overlap region II, which can be calculated using Eqs. (2) and (17) :

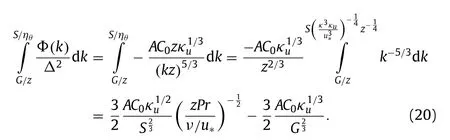
Since the spectrumΦ(k)has a continuous form at the integral boundaryG, we have

The fourth term in Eq. (18) is from the diffusivity at very small length scales and is assumed to be negligibly small.

Finally, taking all the contributions from various spectral regions as discussed above into Eq. (18) , the normalized temperature variance is given by

wherez∗≡zu∗/νis the scaled distance from the plate,M1andC1are universal constants andN1is a large-scalecharacteristic constant. Usingλth≡L/(2Nu)(Nuis the dimensionless global heat transfer through the sample) as the “wall unit”for temperature profiles [10] , we havez+≡z/λth. Then the above equation can be rewritten as

where

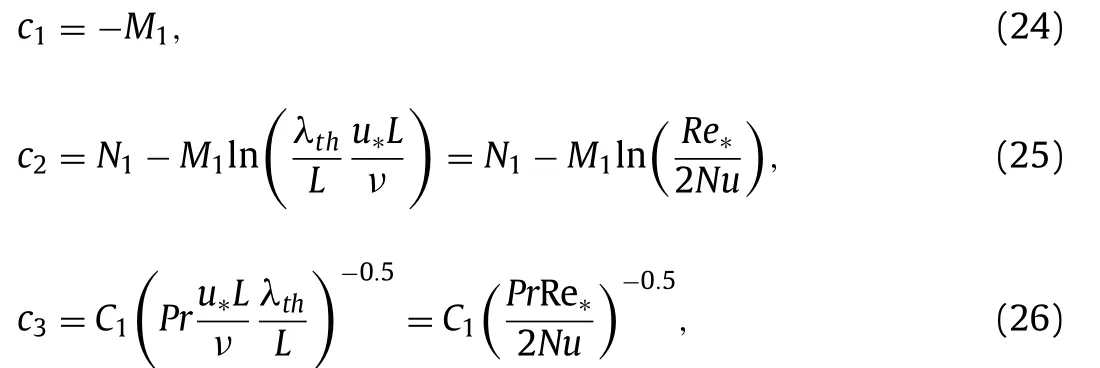
are three parameters to be determined from experimental data.Here the Reynolds numberRe∗=u∗L/ν. Note that whenPrapproaches infinite, the power-law term in Eq. (23) vanishes and the temperature variance will solely follow the logarithmic profile. Although we suppressed explicit mention of any radial dependence,we should of course expectandto depend onr.

According to Eq. (24) the coefficient of the logarithmic termc1is independent ofRa. Eqs. (25) and (26) indicate that the other two coefficients do depend onRaviaRe∗/Nu; but estimates ofRe∗based on Ref. [11] indicate that this dependence is extremely weak.Thus the primaryRadependence entering into Eq. (23) comes fromλthviaNu(Ra), and we expect that a plot ofσ2vs.z+=z/λthshould be essentially independent ofRa.

In conclusion, we applied the “attached eddy”idea for velocity fluctuations in shear-flow turbulence to temperature fluctuations in turbulent RBC. Based on various scaling laws of the temperature spectrumΦ(k), we derived a general equation for the temperature varianceσ2(z). The obtainedσ2(z)equation includes logarithmic and a power-law terms. The logarithmic term results from the scaling ofΦ(k)～k−1while the power-law term comes fromΦ(k)～k−5/3. Both scalings were found in the temperature frequency spectra measured in RBC at highRa[12] . We note that on the basis of the elliptic approximation for correlation functions [ 13 , 14 ], the scaling of the temperature frequency spectra is the same as that of the temperature wavenumber spectra [15] . As a result, one can derive a near-universal form ofσ2as given by Eq. (23) . For RBC flows where thek−1scaling is absent, the logarithmic form is predicted to vanish. In this case, the temperature variance profileσ2(z)predominantly follows a power-law functional form.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

X.He acknowledges the support of the National Natural Science Foundation of China (Grants 11772111 and91952101 )andtheMax Planck Partner Group.