Derivation of FFT numerical bounds of the effective properties of composites and polycristals

Minh-Tan Nguyen , Quy-Dong To , Vincent Monchiet

Univ Gustave Eiffel, Univ Paris Est Creteil, CNRS, MSME UMR 8208, F-77454 Marne-la-VallÃl’e, France

Keywords: Composites Homogenization Fast Fourier transform Numerical bounds

A B S T R A C T In this paper, we provide exact fast Fourier transform (FFT)-based numerical bounds for the elastic properties of composites having arbitrary microstructures. Two bounds, an upper and a lower, are derived by considering usual variational principles based on the strain and the stress potentials. The bounds are computed by solving the Lippmann-Schwinger equation together with the shape coefficients which allow an exact description of the microstructure of the composite. These coefficients are the exact Fourier transform of the characteristic functions of the phases. In this study, the geometry of the microstructure is approximated by polygonals (two-dimensional, 2D objects) and by polyhedrons (three-dimensional, 3D objects) for which exact expressions of the shape coefficients are available. Various applications are presented in the paper showing the relevance of the approach. In the first benchmark example, we consider the case of a composite with fibers. The effective elastic coefficients ares derived and compared, considering the exact shape coefficient of the circular inclusion and its approximation with a polygonal. Next, the homogenized elastic coefficients are derived for a composite reinforced by 2D flower-shaped inclusions and with 3D toroidal-shaped inclusions. Finally, the method is applied to polycristals considering Voronoi tessellations for which the description with polygonals and polyhedrons becomes exact. The comparison with the original FFT method of Moulinec and Suquet is provided in order to show the relevance of these numerical bounds.

An alternative approach to finite elements methods (FEM) has been proposed in the middle of the nineties by Moulinec ans Suquet [1] for the computation of the effective properties of elastic composites. The unit cell problem is solved by means of an iterative scheme which uses the periodic Green tensor for the strain and could be directly applied to digital images which come from modern devices such asμ−tomograpy. An alternative approach based on the form factors or the shape coefficients (following the terminology used in the book of Nemat-Nasser [2] ) has been developed by Bonnet [3] to improve the fast Fourier transform (FFT) solutions. The shape coefficients are the exact expressions of the Fourier transform of the characteristic functions of the phase. Closed-form expressions are available for inclusions having ellipsoidal shapes [2] and have been later considered to improve the FFT solutions in the case of a composite with aligned cylindrical fibers [3] . Note that the shape coefficients are also the basis of recent closed-form approximation expressions of effective properties of periodic composites [ 4 , 5 ]. Accordingly to Ref. [3] , for many problems, the microstructure geometry is only approximated when using the Moulinec and Suquet method [1] . As for example, in the case of a composite with fibers, the cross section geometry is approximated with squared pixels which leads to a poor approximation of the real geometry and introduces corners which reduce the convergence of the method. Note that an alternative approach consists to use composite pixels [6–9] . Later, it has been demonstrated that the use of the shape coefficients in the FFT “strain”and “stress”based iterative schemes provides rigorous bounds of the effective elastic properties of the composites [10] . The method has been also recently extended to the case of composites with interface discontinuities [11] .

However, the method based on shape coefficients is restricted to composites with ellipsoidal inclusions which considerably reduces the capacity of the approach. In this paper, we propose to extend the method to arbitrary microstructures, making use of recent results [12] on the shape coefficients for polygons and polyhedrons. Such expressions are the basis of the approximation used in that paper to describe the geometry of the inclusions; leading obviously to better approximation than pixels. Note that such approximation is also the basis of the finite element method since each interface is discretized with a finite number of nodes connected by segments (in two-dimensional, 2D). The benchmark problem of a circular inclusion is first considered: the solution with the exact shape coefficient [3] is compared with the solution based on equilateral polygons. Next, we apply the approach to the case of a composite with ”flower shaped”and toroidal inclusions. Finally,we apply the approach to polycrystals simulated by Voronoi tesselations for which the description with polygones (in 2D) and polyhedrons (in three-dimensional, 3D) is exact. Through these different examples, the FFT numerical bounds are compared with the solution derived with the original method of Moulinec and Suquet[1] .

We consider a heterogeneous elastic material defined by a parallelepipedic unit cell and three (two for plane strain or plane stress problems) vectors of translation invariance. The unit cell is made up ofMphases whose elastic (resp. compliance) tensors are denoted by Cα(resp. Sα=(Cα)−1) withα= 1, 2, ...,M. Classically,the local problem involves the compatibility equations, the linear elastic constitutive law, the equilibrium and the periodic conditions at the boundary of the unit cell:

in which the stiffness tensor C(x)(resp. the compliance S(x)) of the heterogeneous medium is given by:

forα= 1, 2,...,Mare the characteristic functions associated with the phasesVα, they satisfy toPrescribed macroscopic strainE= 〈ε〉Vor macroscopic stressΣ= 〈σ〉Vare classically considered.

Variational principles based on the macroscopic elastic energy could be considered to determine a lower and an upper bound for the effective elastic coefficients of the composites. Following Ref.[10] , the discretization is performed with truncated Fourier series for the strain or the stress. Thus, for any real quantityfwe put:

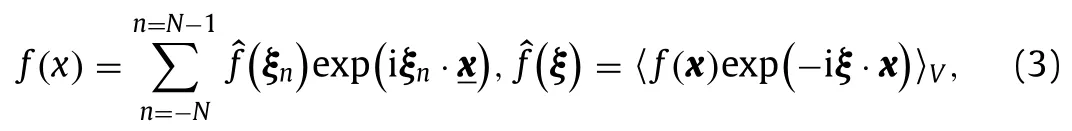
where 〈·〉Vdenotes the volume average of the quantity “·”over the volumeVof the unit cell. Moreover,ξnforn= −N, −N+ 1, ...,N−1 denote the discrete wave vectors given by:

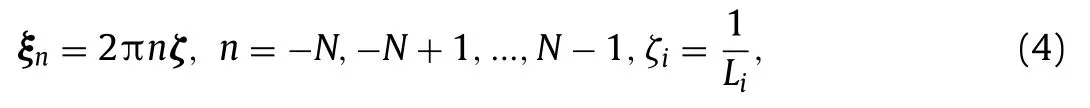
andL1,L2,L3are the dimensions of the cell along the three space directionsx1,x2andx3. Obviously, the problem is discretized along each space direction, this would involve the use of two indicesn1andn2for 2D problems and three for 3D one. However, only one indicenis used for simplicity. Still for simplicity, we shall use the notationthe Fourier transform offassociated with the wave vectorParticularly, the Fourier component corresponding ton= 0 of the quantityrepresents its average over the volume of the cell,For instance, we haveand

The stationarity point of the strain based potential with respect tocan be computed with the following recurrence relation (all the details about the demonstration could be found in Ref. [10] ):

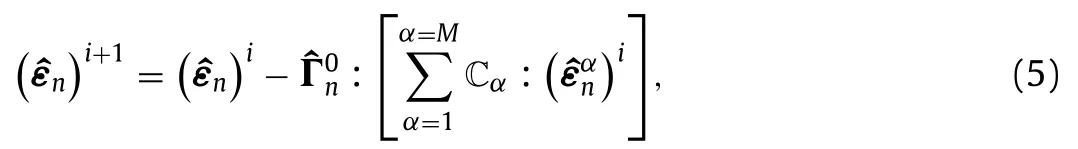
which starts withforandNote that the iterative scheme has the same general structure than that already provided by Moulinec and Suquet [1] . Particularly, it uses the same expression for the Green tensorΓ0, the latter is explicitly known in the Fourier space and can be found for instance in Refs.[ 1 , 10 , 13 , 14 ]. The difference with the scheme of Moulinec and Suquet [1] lies in the calculation of the elastic response of the composite. In the present iterative scheme, it involves the computation ofat each iteration by computing the discrete convolution product between the shape coefficient of the phaseαwith the strainThe discrete convolution product reads:

A lower bound for the homogenized elastic tensor is computed with the stress based iterative scheme. This scheme has been formulated by Refs. [ 3 , 15 ], it uses the compliance tensors Sαforα= 1, 2, ...,Mand the dual, stress based, Green operatorΔ0:

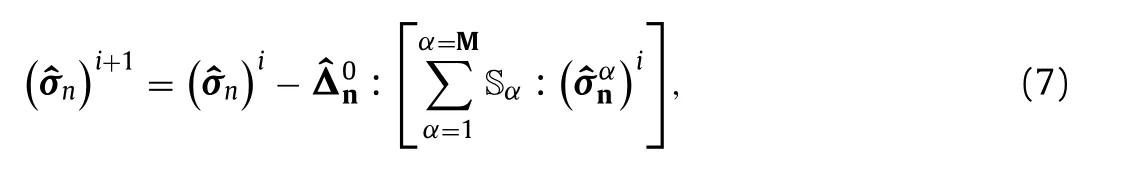
It must be emphasized that the main differences between the present FFT iterative schemes and that of Moulinec and Suquet[ 1 , 13 ] lies in the use of the shape coefficients to make the convolution product in Eq. (6) . Indeed, in the Moulinec-Suquet approach[ 1 , 13 ], the inverse FFT ofis computed to obtainthat represents the strain at the nodes of a regularly spaced grid in the real space. The latter is multiplied by the characteristic functionheredenote the position of the nodes of the grid. As a consequence, the real geometry is then replaced by voxels. The bound property of the solutions is ensured if the exact expression ofis used. Formally, we haveexcept for an infinite number of wave vectors. By increasing the number of wave numbers, the two methods converge to the same solution.The two methods are then equivalent for infinite number of wave vectors but differs at finite number. With the shape coefficients, it is possible to enclose the exact solution at any value of the wave number while, however, with the Moulinec-Suquet method, only an estimate of the solution is computed, neither an upper bound nor a lower bound. In addition, it will be shown in the numerical examples, that the Bhattacharya-Suquet stress based iterative scheme [15] (the stress based counterpart of the Moulinec-Suquet method) leads to the same estimation of the homogenized elastic properties.

Note also that sincenandmvary from −NtoN−1, thenn−mvaries from −2Nto 2N−2 in Eq. (6) . As a consequencemust be computed on a double grid (dimension is 4N×4N) while the coefficientsare computed on the simple grid (dimension is 2N×2N). The componentsmust be computed before the iteration process and stored. The procedure is computationally more expensive than the original scheme [1] because the convolution product is made on the double grid while the former method uses a representation of the elasticity tensor on the simple grid. To conclude, the bound character of the solutions requires: (i) to use the exact expressions of the shape coefficients, (ii) to make the discrete convolution product on the double grid. More details about the numerical implementation of the discrete convolution product on the double grid could be found in Ref. [10] . In the next section we discuss more about the shape coefficient. At this stage, it must be recalled that the shape coefficients are only known in the case of ellipsoids. For other inclusion shapes, we propose to approximate with polygons and polyhedrons.

The shape coefficient of the phasesVαis the Fourier transform of the characteristic functionIα(x). It is denotedFirst, note that the Fourier coefficient corresponding ton= 0 represents the volume average of the corresponding quantity. It follows that:

wherecα=Vα/Vrepresents the volume fraction of the phase of volumeVα.

Due to the property:

It can be deduced that:

This means that, for a two-phase composite, the shape coeffi-cient of the matrix is known as soon as that of the inclusion phase is known.

Considera polygon in the plane (e1,e2) where (e1,e2,e3) is the cartesian frame ande3is orthogonal to the polygon. Let us denote the positions of its corners byr1,r2,...,rJ, the corners being numbered in counter-clockwise direction and their total number isJ.The shape functionof the polygon is given,, by:

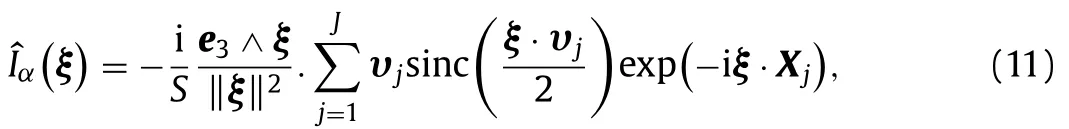
in which ‖ξ‖ denotes the norm ofξ,υj=(rj−rj−1)andXj=defines the center of the segment (rj−1,rj) (see Fig. 1) , also the conventionr0=rJmust be applied in the summation overjin Eq. (11) . MoreoverSrepresents the area of the unit cell which is taken equal to 1 in our computations. In Eq. (11) , “sinc”is the cardinal sine function (defined by sinc(x) = sin(x)/x). Note that in Ref. [12] , various expressions for the shape coefficients of polygons are provided and they are all mathematically equivalent. However the expression given by Eq. (11) is the most convenient for the numerical, implementation since it uses the cardinal sine that admits the limit sincξ·υj/2 = 1 whenξ·υj= 0 . Indeed, during the numerical integration of the shape coefficient the factorξ·υjcan be null or very close to zero when a wave vectorξis orthogonal to an edge. For instance, if an edge is oriented along thex1-axis, the factorξ·υjis null for all the wave vectors corresponding toξ1= 0.Expressions given by Eq. (11) takes appropriately the limit in such situation.

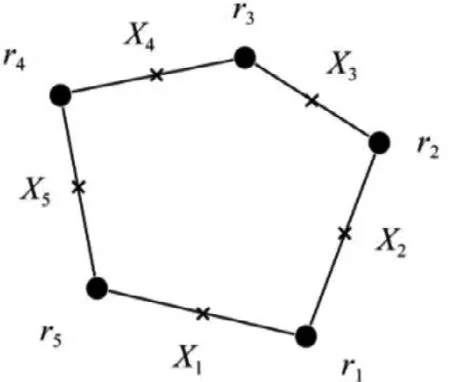
Fig. 1. Positions and centers of the edges of the polygonal.

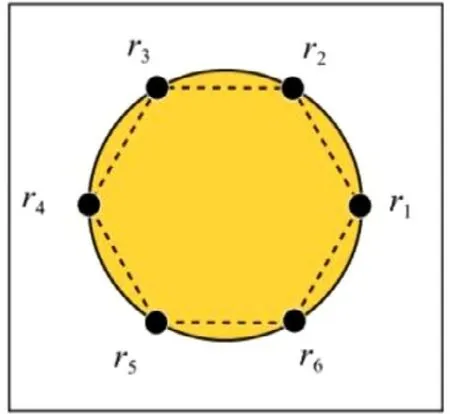
Fig. 2. Unit cell of the composite with a circular inclusion. Approximation of the shape of the inclusion with a regular polygon.

Whenξ= 0, the shape coefficient of the polygon iswhereAdenotes the area of the polygon defined by:

A polyhedron is defined by itsKflat faces denotedΓkfork= 1,2, ...,K. Each faceΓkis aJk-polygon given by the simple polygonal vertex chain (rk,1,rk,2, ... ,rk,J) and by the normal unit vectornkof the polyhedron that pointing towards outside the polyhedron.From a practical point of view, when implementing the method,the mesh on the boundary of the inclusion can be obtained from a mesh generator software, a numerical test can be applied to check that all points of the polygonal chain of the simple polygon are coplanar. The test consists to check that the quantity

is independent ofj. Note thatDkrepresents the distance from the origin of the cartesian frame to the plane that contains the polygonalΓk.

The shape coefficient of theα-polyhedron isand ∀ξsuch that·nk:

whereVdenotes the volume of the unit cell and:

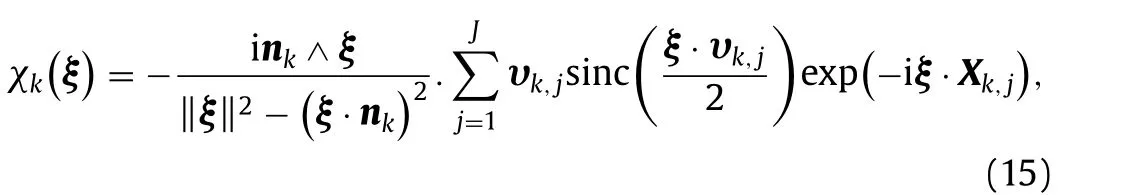
withanddefines the center of the segment(rk,j−1−rk,j). The conventionmust be used in the summation overjin Eq. (15) . Note thatχk(ξ)is the 2D-shape function of the facetkof the polyhedron.

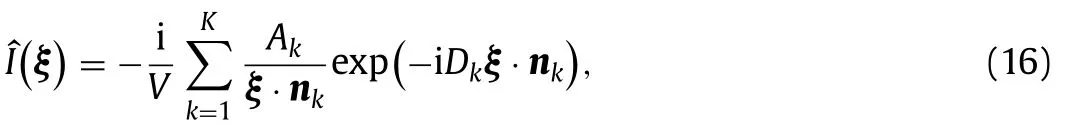
whereAkis the area of the polygonalΓkandDkis given by Eq. (13) .

Finally, whenξ= 0 , the shape coefficient isIα(ξ) =Ω/Vin whichΩis the volume of a the polyhedron which can be conveniently computed from:

From a numerical point of view, during the computation of the shape function, we need to test if the discrete wave vectors are colinear to the normal unit vectornkof the polygonalΓk. If it is, the alternative expression given by Eq. (16) must be used. Note that the wave vectors are discretized along each space direction with 2Nwave numbersn= −N,-N+1,...,N−1 (see Eq. (4) ), then a total of (2N)3wave vectors are considered. Moreover, the boundary of the inclusion must be discretized with a large number of facets and for each one we must check if the (2N)3wave vectors are colinear to the normal unit vectornkto the facet. A more efficient and economic method is proposed below.

Let us denote:

Whenξis colinear tonk, the quantityBk(ξ) is null and the shape coefficient must be computed with expression (16). let us introduce the functionYk(ξ,∊)defined by:

whereH(x) is the heaviside function:

Then, we propose to replaceBk(ξ) by the quantity:

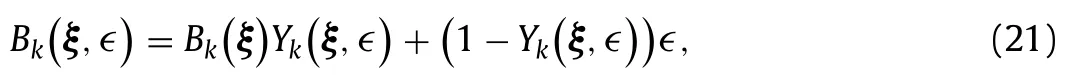
which is equivalent to:

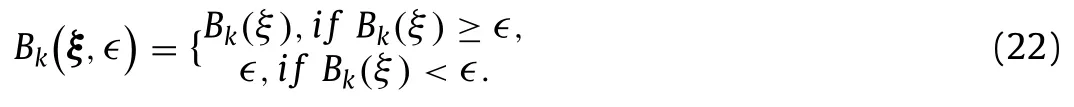
As a consequence, all the values ofBk(ξ) inferior to∊are replaced by the value∊in the expression ofBk(ξ,∊). It must be emphasized thatBk(ξ) is obtained as the limit ofBk(ξ,∊)for∊→ 0 .The main idea of the approach is to eliminate the singularity in the expression ofχk(ξ)given by Eq. (15) by replacing the factorthat is strictly positive owing to expression (22).

Let us now replace in Eq. (14) the termχk(ξ)by:

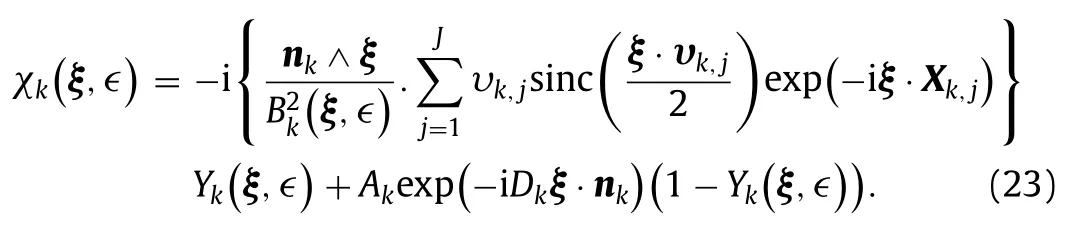
Advantageously, we have only on expression for the shape function considering Eq. (13) in whichχk(ξ)is replaced byχk(ξ,∊).With this substitution, the singularity for ‖ξ‖ =ξ·nkis removed.The numerical tests show thatχk(ξ,∊)andχk(ξ)are equal by considering the value∊= 10−3.

In order to validate the approach, we consider the simple case of a composite with circular inclusions (see Fig. 2 . Each phase is assumed to be isotropic; the elastic coefficients of the matrix areλ1= 1,μ1, that of the inclusion areλ2= 10 andμ2= 10. The index “1”makes reference to the matrix while index “2”makes reference to the inclusion phase. The radius of the inclusion isR= 0.25,the dimension of the unit cell is 1 along each space direction.

Fig. 4. Composite with one (left) and multiple (right) flower shape inclusions.

The exact shape coefficient for a circular inclusion can be found in Ref. [4] and is expressed with the Bessel function of the first kind and first orderJ1:

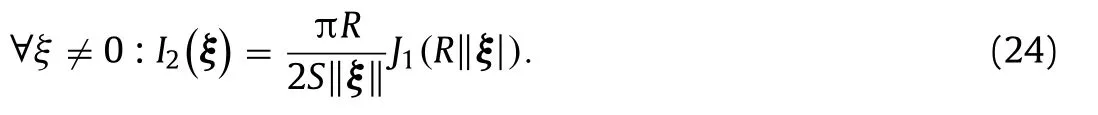
Forξ= 0, the shape coefficient isI2 (ξ) =πR2/S. The area of the unit cell isS= 1 for the numerical application.

Alternatively, we approximate the shape coefficient with a regular polygon by considering a discretization with nodes evenly spaced on the boundary of the circle (see Fig. 2 ). The number of edges isJ, equal to the number of nodes and all edges have the same length.

In Fig. 3 , the left subfigure shows the macroscopic elastic coefficientC11 (in Kelvin notation [16] ) as function of the number of polygonal edgesJ. The solution tends asymptotically to the exact shape coefficient whenJincreases. The relative error between the two solutions is provided in Fig. 3 (at the right). It is observed a good convergence, the relative error is of order 10−4by consideringJ= 100 edges.

The method is now applied to a composite with inclusions having a flower shape. In Fig. 4 , we show a unit cell containing a single flower shape inclusion centered at the origin (on the left) and a population of flower shape inclusions (on the right). The geometry of a single inclusion is obtained considering a boundary delimited by the coordinatesx1=ρ(θ) cos(θ),x2=ρ(θ) sin(θ) withρ(θ) =Rcos(2θ) andR= 0.25. In the case of multiple inclusions,we use the same parametrized function withR= 0.15 and the population is generated by considering the translation property of the Fourier transform. Specifically, the shape coefficient of a flower located atx=Xis computed from that located at the origin and by multiplying it by the factor “exp(iξ·X)”. From a numerical point of view, the shape coefficient of a single centered flower inclusion is first computed. Next, the shape coefficient for the population of inclusions is obtained by multiplying the aforementioned shape coefficient by the factorwhereXirepresents the positions of the inclusions. For the simulations, we use the same elastic coefficients that for the circular inclusion.

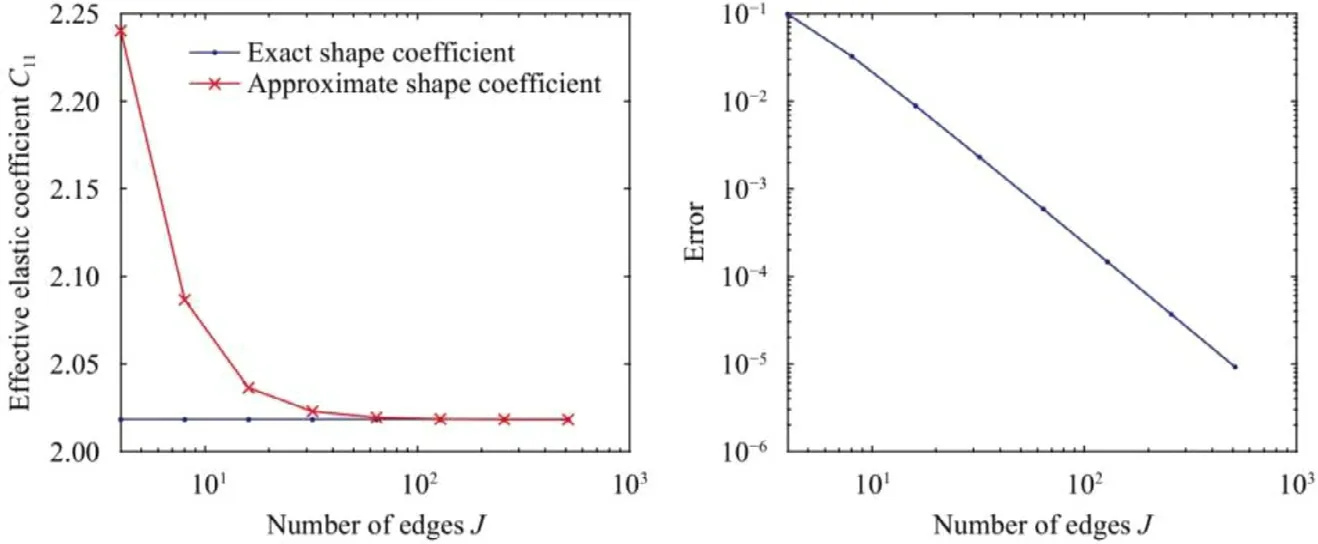
Fig. 3. Left: variations of the effective elastic coefficient C 11 as function of the number of edges J (for the polygonal approximation) and its comparison with the solution with the exact shape coefficient. Right: relative error between the two solutions (using the approximate and exact shape coefficient of the inclusion).

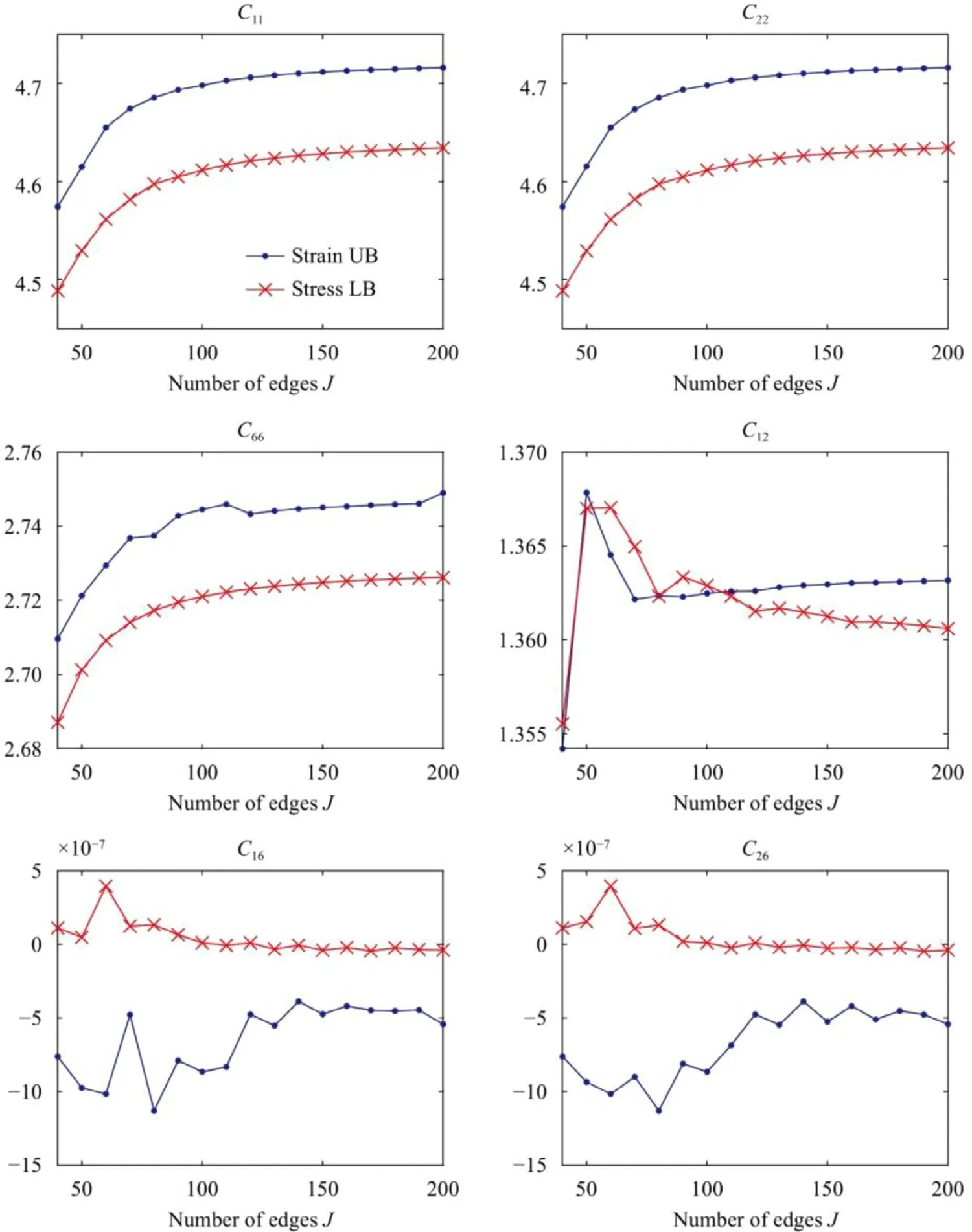
Fig. 5. Variation of the effective elastic coefficients obtained with the two bounds as function of the number of edges.

We consider a unit cell containing a flower-shape inclusion centered at the origin (see Fig. 4 at the left). The variations of the elastic moduli with the number of edges is represented in Fig. 5 for the two bounds: the strain based upper bound (“strain UB”in Fig. 5 ), the stress based lower bound (“stress LB”in Fig. 5 ). The number of wave vectors isN= 128. A good convergence is observed forJ= 200 edges. This value is used thereafter to compare the different solutions.

We now consider the case of a composite with a population of inclusions (see Fig. 4 at the right). Figure 6 shows the results for the effective elastic coefficients withJ= 200 as function of the wave numberNtaken along each space directions. We compare the two bounds with the solution computed with the strain based FFT iterative scheme of Moulinec-Suquet [1] (denoted “strain MS”in the legend). Also, we provide the results obtained with the dual”stress based”iterative of Bhattacharya-Suquet scheme [16] which also uses a description of the microstructure with pixels in the real space (denoted “stress BS”in the legend). It is first observed that the two FFT numerical bounds have a uniform convergence. Moreover, the iterative shemes of Moulinec-Suquet and Bhattacharya-Suquet lead to the same estimates of the effective properties of the composite which are comprised between the two bounds.

We consider a composite constituted of toroidal inclusions with axis of revolution aligned along thex3-axis. The coordinates of the surface are given by:

withθ= [0, 2 π] andφ= [ 0,2 π] . The parametersRandrare known as the major and the minor radius. WhileRis the distance from the center of the tube to the center of the torus,ris the radius of the tube. Since there is no available analytic expression for the shape coefficient in the literature, the geometry is then approximated by polyhedrons. In our numerical applications, we chooseR= 0.25 andr= 0.1, the dimension of the cuboidal unit cell isL= 1. The unit cell contains one toroidal inclusion centered at the origin. The surface of the torus is discretized by consideringpdiscrete values regularly distributed in the interval [0,2π] for bothθandφ. The surface of the toroidal inclusion is then described byK=p×pfacets as shown in Fig. 7 .

Fig. 7. Toroidal inclusion with K = 10 ×10 facets and K = 30 ×30 facets.

The computation of the homogenized elastic coefficients are performed by consideringμ1=λ1= 1 in the matrix andμ2=λ2= 10 in the inclusion. In Fig. 8 we represent the componentsC11,C33,C12,C13,C44andC66as function of the number of facetsK. In these figures, we provide the upper bound (UB) obtained with the strain based iterative scheme and the lower bound(LB) obtained with the stress based iterative scheme and we show their variations with respect to the value of the wave numberN.The unit cell having the two following symmetries: (i) the invariance by the reflection with respect to the three mutually orthogonal planes oriented along the axes of the cartesian frame, (ii) the invariance by rotation of an angle π/4 around thex3-axis, the resulting homogenized elastic matrix is orthotropic. This implies thatandNote that the material is also close to transverse isotropy, we havethat is rigorously satisfied only if the material is invariant by any rotation around thex3 -axis, that is not true due to the spatial distribution of the inclusions. In the considered problem, the distance between two neighboring inclusions is large enough to neglect the interaction effects and to recover the transverse isotropy. It is observed a uniform convergence of the bounds, particularly forC13andC33. The lower bound has converged forN= 32 which suggests that it is close to the exact solution. The convergence of the homogenized elastic coefficients is observed for a number of facets up toK≃ 50 ×50 .

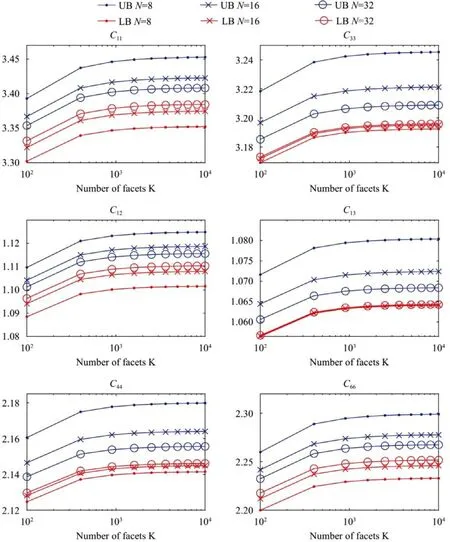
Fig. 8. Effective coefficients of the composite with toroidal inclusions. Comparison of the solutions obtained with the upper bound (UB), the lower bound (LB) as function of the number of facets for different values of wave number N .

Another interesting applications for which the description with polygons and polyhedrons are exact is the case of polycristals generated by Voronoi tessellations. In the 2D case, each single crystal is then represented by a polygon in the planeVectoris normal to the plane. The polycrystal is made up ofMsingle cubic-crystals. The elastic matrix of the crystalαin the global cartesian frame iswhereCis the elastic matrix of the cubic crystal written in the frame of cristallographic directions:

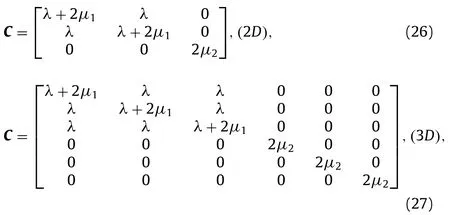
The computations are performed with the following values of the local elastic moduli:μ1= 1,μ2= 2 andλ= 1. The matrix of rotationRαdepends on the crystal orientation. The crystallographic texture is assumed to be uniformly random. In 2D case, the orientation of each crystal is defined by an angleθrandomly chosen in the interval [0,π]. A representative cell of the polycristal is represented in Fig. 9 . Three angles are used in the 3D case, a representative cell of the polycristal is represented in Fig. 9 . It is possible to impose a geometrical periodicity constraint at the boundary of the unit cell. It results in a slight decrease of the dispersion of the apparent properties when compared to simulations relying on the initial Voronoi model. In this example, the calculations are performed on 40 samples and the effective shear modulus is determined by the classic ensemble average rule.

The variations of the homogenized shear modulus with the number of wave vectors are provided in Fig. 10 in 2D case (left)and in 3D case (right). The two numerical bounds are compared with the solutions computed with the iterative sheme of Moulinec and Suquet. The solution with the dual iterative of Bhattacharya and Suquet scheme is not presented because it leads to the same values of the effective elastic coefficients. Again, we observe that the solution obtained with the FFT scheme of Moulinec and Suquet is comprised between the two numerical bounds. Note that only the shear modulus is represented in the figures, the macroscopic compressibility being equal to the local compressibility for polycrystals.

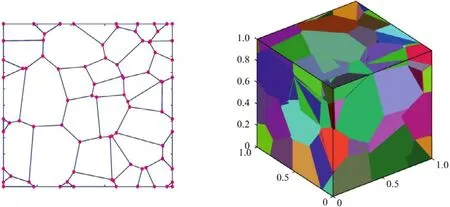
Fig. 9. Unit cells of the Voronoi periodic structure. 2D case at the left and 3D case at the right.

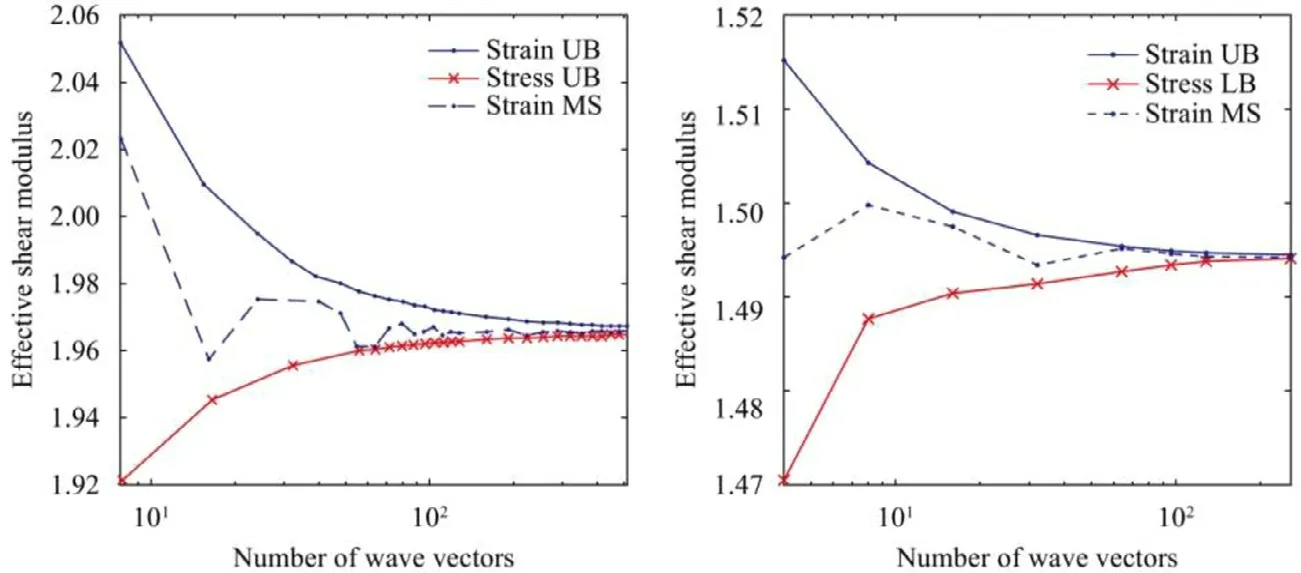
Fig. 10. Variations of the effective shear modulus μhom as function of the number of wave vectors.

In this paper, we extend the FFT-based numerical method based of shape coefficients to arbitrary microstructure. The use of these shape coefficients allows to deliver a lower and an upper bound for the effective properties of composites and polycrystals. For arbitrary microstructure, the phases are meshed by polygons in 2D case and by polyhedrons in 3D case for which the shape coeffi-cients are explicitly known. The approach is applied to a composite with circular and flower-shaped inclusions. Then, the method is applied to polycristals generated by Voronoi tesselations. It has been shown that the numerical bounds have a uniform convergence with the number of wave vectors. The results are compared to that computed with the original scheme of Moulinec and Suquet which approximates the microstructure with pixels in the real space. It has been found that the results with the latter approach are comprised between the two bounds.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.