Analytical solutions for sediment concentration in waves based on linear diffusivity

YiqinXie Jifu Zhou ∗ Xu Wng Ynrong Kui Yongjun Lu

a Key laboratory for Mechanics in Fluid Solid Coupling Systems, Institute of Mechanics, Chinese Academy of Sciences, Beijing, China

b School of Engineering Sciences, University of Chinese Academy of Sciences, Beijing, China

c State Key Lab Hydrol Water Resources&Hydraul En, Nanjing Hydraulic Research Institute, Nanjing, Jiangsu 210024, China

Keywords: Analytical solution Wave-induced sediment concentration Reference concentration Pickup function Sediment diffusivity

A B S T R A C T T wo kinds of analytical solutions are derived through Laplace transform for the equation that governs wave-induced suspended sediment concentration with linear sediment diffusivity under two kinds of bottom boundary conditions, namely the reference concentration (Dirichlet) and pickup function (Numann), based on a variable transformation that is worked out to transform the governing equation into a modified Bessel equation. The ability of the two analytical solutions to describe the profiles of suspended sediment concentration is discussed by comparing with different experimental data. And it is demonstrated that the two analytical solutions can well describe the process of wave-induced suspended sediment concentration, including the amplitude and phase and vertical profile of sediment concentration. Furthermore, the solution with boundary condition of pickup function provides better results than that of reference concentration in terms of the phase-dependent variation of concentration.

Sediment transport induced by waves is an advanced subject in coastal hydrodynamics, which is of great significance to coastal engineering. Suspended sediment transport is of particular importance for the design and maintenance of waterway and harbors.

There have been a few researches on the analytical solution of the vertical distribution of suspended sediment concentration based on advection-diffusion equation for steady flows [1–6] or periodical averaged advection-diffusion equation for waves [ 7 , 8 ].These previous works are based on steady or quasi-steady concept and are of course unable to reveal the unsteady characteristics of wave-induced suspended sediment concentration.

Therefore, some investigators turned to pay attention on the unsteady characteristics of wave-induced suspended sediment concentration based on unsteady advection-diffusion equation [9–12] .These researches either present analytical solutions of advectiondiffusion equation with constant diffusion coefficient, or directly model the process by numerical approach for the case of variable diffusion coefficient. In the present study, analytical solutions of time-dependent suspended sediment concentration induced by waves is derived for the case of variable diffusion coefficient that varies linearly in the vertical direction.

In general, the horizontal gradients of sediment concentration are negligible because it is much smaller relative to the vertical gradients [10] . Based on the gradient transport hypothesis, the vertical distribution of instantaneous suspended sediment concentration induced by waves is generally given by the following equation[13]

wheretis the time, andzis the vertical coordinate (positive upward from the bottom of computational domain, as shown in Fig. 1 ),cis the suspended sediment concentration,wsis the settling velocity of sediment,εsis the sediment diffusion coefficient.

Fig. 1 presents three expressions of sediment diffusivity for waves, which are commonly used for waves propagating over rippled and rough sand bed, including constant, three layered and linear distributions [14] . It is easy to get the analytical solution for suspended sediment equation when the sediment diffusivity is constant [9] . Moreover, the expression of three layered sediment diffusivity can be deemed as the combination of constant and linear distributions, and the analytical solution can be easily achieved based on the solutions for constant and linear expressions. Therefore, the linear sediment diffusivity for waves is chosen to study the suspended sediment concentration, which is expressed [ 8 , 15 ]as

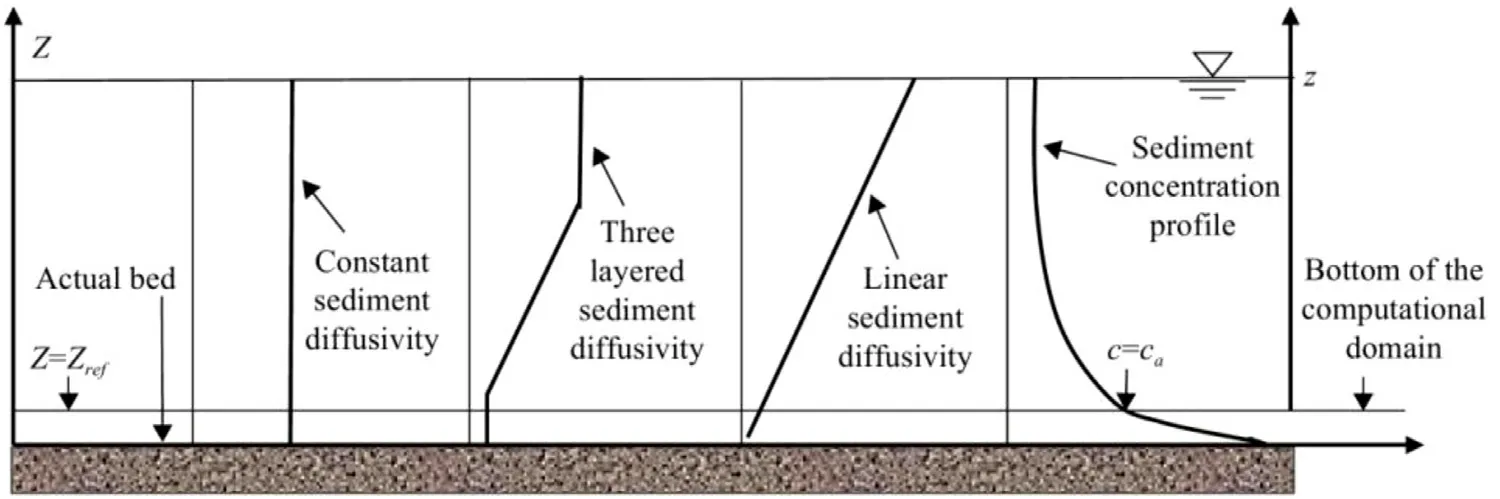
Fig. 1. Schematic representation of sediment diffusivity, sediment concentration profile and near-bed boundary.

whereis the mean value of periodic bottom friction velocity,Z>0 is the vertical coordinate of the origin at actual bed, as shown in Fig. 1 ,βreflects the efficiency of entraining sediment into suspension and is an adjustable parameter. As shown in Fig. 1 , the plane bed is generally adopted even if the actual bed is rough or rippled. Through parameterization, a ripple bed can also be dealt as plane bed. Furthermore, the bottom of computational domain differs from the actual bed by a reference height (Zref), whereZrefis frequently set to 0.01 m [ 16 , 17 ]. For the sake of discussion, the sediment diffusivity is rewritten asεs=az+b, whereand

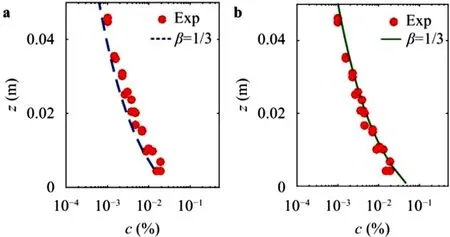
Fig. 2. Comparison between analytical (line) and experimental (circle) results of oscillatory flow.

Initially, the clear water is considered and the initial sediment concentration is set to zero. For boundary conditions, the sediment concentration at the top boundary is zero as employed by [1] . And the reference concentration (Dirichlet) and pickup function (Neumann) are considered at the bottom boundary, respectively.

The Dirichlet bottom condition is

whereca(t)is the time-dependent reference concentration, which is a function of bottom shear stress, following Ref. [17]

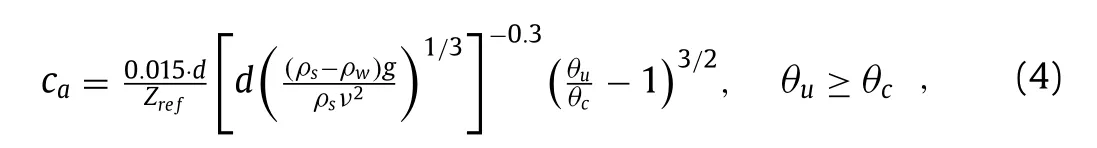
wherecais set to zero whenθu<θc,dis sediment diameter,ρwis water density,ρs= 2650 kg/m3is the sediment density,gis the acceleration of gravity,νis the kinematic viscosity coefficient,wsis the sediment settling velocity in the vertical direction [18] ,θcis the critical shields number for incipient motion [18] ,θu=τ/[(ρs−ρw)gd·(1 −πηr/λr)2] is the Shields number andηris the ripple height,λris the ripple length.τis the bottom shear stress which can be referred to Ref. [19] for specific calculated method.

As an alternative of the Dirichlet condition, the pickup function is adopted to specify the vertical gradient of sediment concentration at the reference height, serving as the Numann condition as follows [20]

Then, let us solve Eq. (1) with linearly varying sediment diffusion coefficient under bottom boundary conditions of Eqs. (3) and( 5 ), respectively. Hereafter, the problems with bottom boundary conditions of Eqs. (3) and ( 5 ) are referred to Type I and Type II,respectively.

Via applying Laplace transform to Eqs. (1) –( 3 ), a second-order ordinary difference equation is obtained

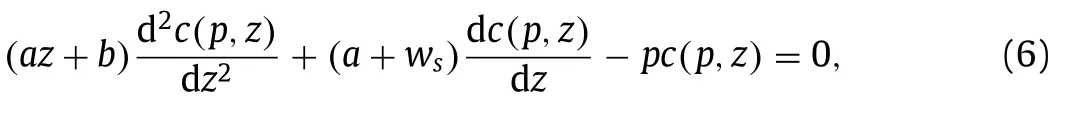
with the boundary conditionc(p,0)=L[ca(t)] , wherepis the parameter generating by Laplace transform andL[•] is the Laplace transform operator.

To solve Eq. (6) , a variable transformation is worked out, which reads

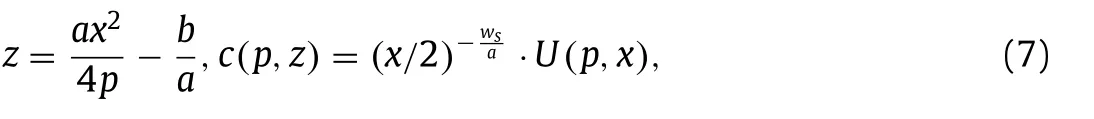
whereU(p,x) is the transformed function, andxis the transformed variation. Inserting Eq. (7) into Eq. (6) leads to the following modified Bessel equation

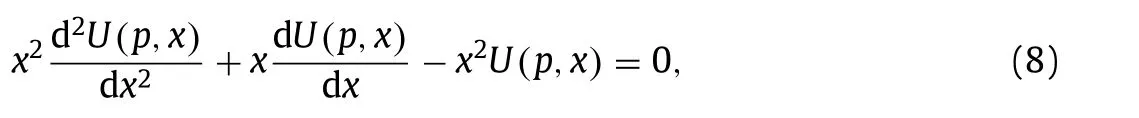
with the boundary condition

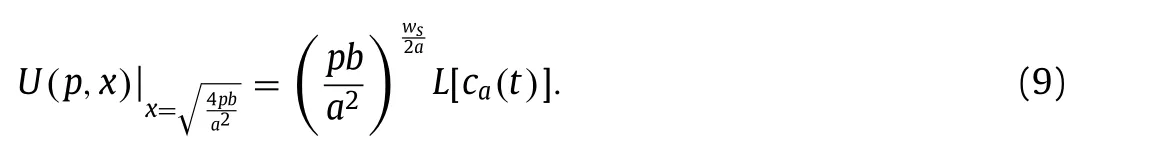
Hence, the solution of Eq. (6) can be obtained in terms of the second-kinds Bessel functions

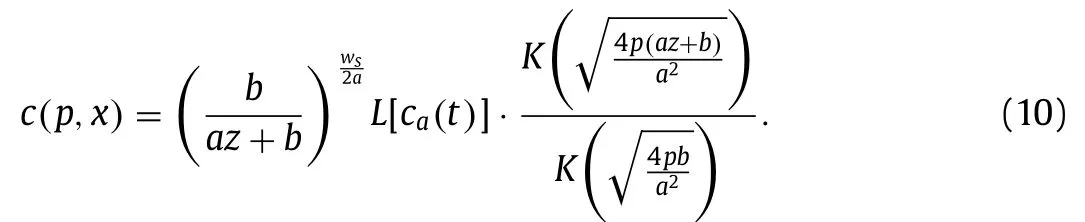
In Eq. (10) , the inverse Laplace transform is difficult to acquire because of the complexity of Bessel function. Hence, the zerothorder asymptotic expression of Bessel function is employed

After submitting Eq. (11) into Eq. (10) and applying the inverse Laplace transform, the final solution of Type I is

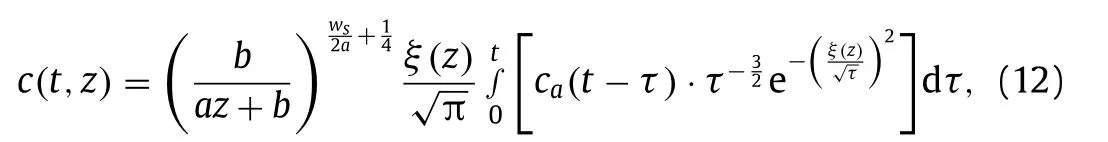
Similarly, the solution of Eqs. (1) and (5) with the linearly varying sediment diffusion coefficient is studied. And applying Laplace transform to Eq. (5) , the bottom boundary condition becomes

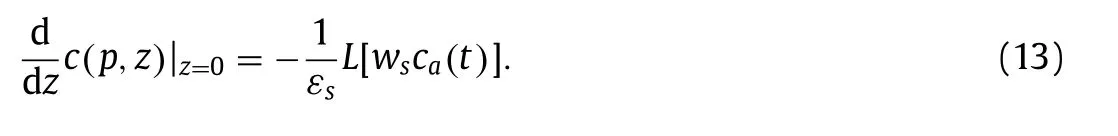
With Eqs. (6) –( 8 ) and (13), the following solution can be derived

Applying Eq. (11) to Eq. (14) and using the inverse Laplace transform, the complete solution of Type II can be reduced as

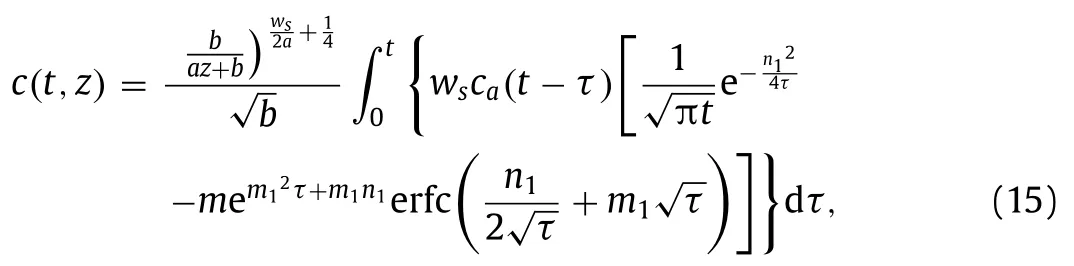
Next, the ability of the two analytical solutions of the suspended sediment concentration equation with two types of bottom boundary conditions are discussed by comparing with different experimental data. The parameters of the experiments are presented in Table 1 , where Test R1 is an oscillatory flow, Test N1 and Test C2 were conducted in laboratory-scale wave flume and field-scale wave flume, respectively.

Table 1 Summary of experiment parameters

Fig. 2 shows the comparison between the analytical results of periodic averaged suspended sediment concentration and experimental data [21] of Test R1, where Fig. 2 a and b represents the results of Types I and II, respectively. As shown in Fig. 2 , the results of Types I and II for the vertical profile of periodic averaged suspended sediment concentration are all in good accordance with the experimental data. Moreover, the results of Type I are slightly bigger than that of Type II for the same value ofβ. Similarly, in Fig.3 , the comparison between the analytical results and experimental data [7] of Test N1 is presented. It shows that both the results of Types I ( Fig. 3 a) and II ( Fig. 3 b) have a good agreement with experimental data for a particular value ofβ.The comparison of the analytical results and experimental data [22] of Test C2 is provided in Fig. 4 , where Exp (1) and (2) represents the experimental data obtained from an acoustic backscatter system (ABS) and a side wall mounted pump sample system, respectively. As shown in Fig. 4 , the results of Types I ( Fig. 4 a) and II ( Fig. 4 b) are still well consistent with experimental data.

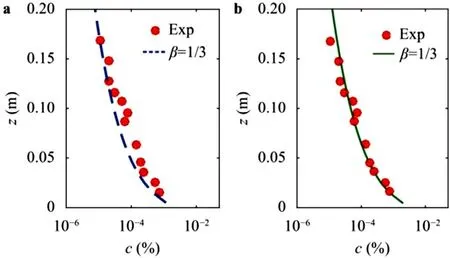
Fig. 3. Comparison between analytical (line) and experimental (circle) results observed from laboratory-scale wave flume.

Fig. 4. Comparison between analytical (line) and experimental (circle and square)results observed from field-scale wave flume.

The comparison of the periodic variation of sediment concentration between the two analytical solutions and experimental data[21]of Test R1 is shown in Fig. 5 , where Subfigs. 5a–c represent the time-dependent sediment concentration atz= 2.1 cm,z= 1.1 cm andz= 0.5 cm, respectively. It is observed that the results of Types I agree well with experimental data whenβ= 0.45 and the results of Types II accord better with experimental data whenβ= 1/3 comparing with Type I, including amplitude and phase. The results of Type I are slightly smaller than that of experiment for the same value ofβ. Moreover, the phases of the concentration of Type II are more consistent with experimental data than that of Type I.

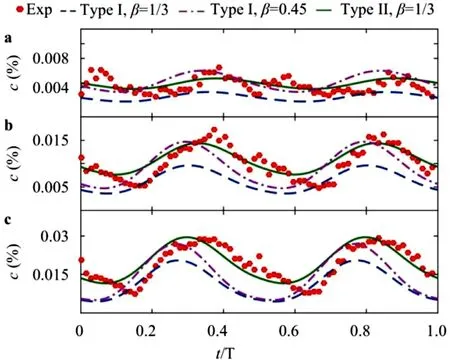
Fig. 5. Comparison of periodic variation of sediment concentration between the analytical results (line) of the two conditions and experimental data (circle) observed from oscillatory flow.

Conclusionly, two analytical solutions for suspended sediment equation with linear sediment diffusivity under two kinds of bottom boundary conditions are derived through Laplace transform,based on a variable transformation that is worked out to transform the governing equation into a modified Bessel equation.

Comparison with experimental data for different conditions has demonstrated evidently that the analytical solutions are capable of describing the time-dependent suspended sediment concentration induced by waves, including the amplitude, phase and vertical profile. In addition, the solution obtained by specifying the bottom boundary condition with pickup function can provide better periodic variation of sediment concentration than with reference concentration.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

We very much appreciate the financial support of the National Key R&D Program of China (2017YFC1404202), the National Natural Science Foundation of China ( 11572332 and 51520105014 ), and the Strategic Priority Research Program of the Chinese Academy of Sciences (XDB22040203 and XDA22040304).