Three dimensional flow motions in the viscous sublayer

S.Santosh Kumar , Xinyi Huang , Xiang Yang , Jiarong Hong , ∗

a Department of Mechanical Engineering, University of Minnesota, Minneapolis, MN, 55455

b Saint Anthony Falls Laboratory, University of Minnesota, Minneapolis, MN, 55414

c Department of Mechanical Engineering, Penn State University, University Park, PA, 16802

Keywords: Viscous sublayer Digital holography Meandering motions Turbulent channel flow Sublayer-scale roughness DNS

A B S T R A C T We employ novel digital Fresnel reflection holography to capture the 3D flows within the viscous sublayer of a smooth-wall turbulent channel flow at Re τ= 400. The measurements reveal unsteady and diverse flow patterns in the sublayer including nearly uniform high and low speed flows and strong small-scale (on the order of viscous wall units) spanwise meandering motions. The probability density functions (PDFs) of wall shear stresses show a clear discrepancy in high stress range with those from direct numerical simulation (DNS), which is attributed to the unresolved streamwise and spanwise motions by DNS. Moreover,the PDF of Lagrangian particle accelerations yields a stretched exponential shape like that in homogenous isotropic turbulence, indicating strong intermittency in the sublayer. We find a significant fraction of high accelerations is associated with the small-scale meandering motions. Our study helps explain the effect of sublayer-scale roughness on reducing drag and flow separation reported in the literature.

1.Introduction

The viscous sublayer is the region of turbulent flow closest to a surface, typically less than five wall units (δν), where viscous effects are dominant. The fluid dynamics in the sublayer directly impacts wall shear stresses and therefore is relevant to the study of fundamental wall-bounded turbulence and its many applications. Using various visualization techniques based on passive tracers such as dust particles, dyes, and hydrogen bubbles, early investigations [1–3] revealed a qualitative picture of unsteady and organized fluid motions within the sublayer including spanwise“sinuous”motions, wall parallel streaks, etc. Subsequently, with the application of hot film anemometry (HFA), several studies investigated quantitatively the mean flow statistics within the sublayer [4–6] and highlighted important trends including the linear profiles of streamwise mean velocity, root-mean-square(rms) of the velocity fluctuation [4] , and the increasing skewness and flatness of velocity distribution as the wall is approached[6] . To overcome the limitations associated with the intrusiveness of HFA, laser Doppler velocimetry (LDV) was implemented later to further examine the sublayer flow, which showed that the turbulence statistics within the sublayer are independent of the Reynolds number [7] and the intensity of velocity fluctuations at the wall asymptotes to a value smaller than the DNS prediction[8] . Despite these effort s, both HFA and LDV being single point measurements can only obtain spatially averaged flow quantities in a sample volume on the order of the viscous length scale (i.e.,viscous wall unitδν) or larger [7 , 9] and thus insufficient to resolve the flow structures within the sublayer.

To overcome these limitations, planar particle image velocimetry (PIV) and particle tracking velocimetry (PTV) were employed for sublayer studies [10–12] . Specifically, through single pixel correlations, Willert [10] resolved the velocity field and the instantaneous wall shear stresses and showed strong time symmetric correlation between the two. Li et al. [11] measured the streamwise velocity fluctuation in the sublayer and found it follows a logarithmic scaling with increasing Reynolds numbers. More recently, Willert et al. [12] captured rare events (less than 0.02%probability) of moving recirculation bubbles within the sublayer.However, the use of a light sheet with a thickness on the order of sublayer scale or larger in PIV and PTV can also lead to spatial averaging similar to those in HFA and LDV, limiting their effectiveness to quantify fine flow structures in the sublayer, particularly,those three-dimensional (3D) motions revealed qualitatively in the early investigations [1–3] .

Acknowledgement of the fine flow structures in the viscous sublayer is vital towards understanding the physical mechanisms involved in the use of sublayer-scale roughness for flow control[13 , 14] . Specifically, surfaces with roughness embedded in the sublayer are generally considered to be hydrodynamically smooth[15] . Nevertheless, Sirovich and Karlsson [13] demonstrated that V-groove roughness (5δνtall, 200δνwide) arranged with random shifts produces a reduction in skin friction, while using uniformly distributed cylindrical pillars ( ～1δνscale) with diverging tips,Evans et al. [14] observed a delay in flow separation in a channel with diverging cross section. To elucidate their mechanisms,a detailed quantification of the 3D flow structures within the sublayer at sufficient spatial and temporal resolutions is needed.However, the state-of-the-art 3D PIV and PTV techniques, including tomographic PIV/PTV [16–19] and holographic PTV [20 , 21] ,have only been implemented successfully for measurements in the logarithmic and buffer layers, owing to constraints in their optical setups and seeding approaches.

Therefore, in this study, we employ a novel in-house developed technique, i.e., digital Fresnel reflection holography (DFRH),for sublayer flow measurements. DFRH records holograms by interfering backscattered light from tracers with the reflection at the wall acting as the reference [22] . Such information is used to determine 3D tracer motions within the sublayer and the corresponding flow statistics. The results from our experiments are compared to a direct numerical simulation (DNS) performed at the same flow conditions. The experiments and DNS are performed on a smooth wall turbulent channel atReτ～400, the complete details for which are included in the supplementary materials .

2.Flow patterns within the viscous sublayer

The tracer particle trajectories are captured in a sample volume of 20δν(streamwise,x) ×20δν(spanwise,z) ×12δν(wall-normal,y) above the wall, with the closest trajectories measured at ～0.1δνto the wall. Fig. 1 presents a compilation of trajectories captured in our experiments, based on which we can identify different flow patterns within the viscous sublayer. Specifically, a large fraction of the flow fields represented by the particle trajectories projected on tox-yplane shows a clear spatial variation of velocity within the sublayer with a sharp drop of streamwise velocity as the wall is approached ( Fig. 1 b). In addition, the corresponding instantaneous velocity profiles do not exhibit a linear behavior with substantial variation along the spanwise direction (Supplementary Fig. 3 and Supplementary Video 1), also indicated by the mixed high and low speed particle tracks at the same elevations in Fig. 1 b. In comparison to streamwise and spanwise motions, the wall normal motions are much weaker within our measurement volume ( Fig. 1 b). The ensemble averaged inclination angle of particle trajectories (calculated as the arctangent of the wall normal displacement to streamwise displacement) is less than 3 °, significantly smaller than the ones reported within the buffer and logarithmic layers ( ～11 °-30 °)[17 , 23] .

In addition, we observe the occurrence of nearly uniform high( Fig. 1 c) and low speed flows ( Fig. 1 d) in the sublayer over 10%of the data. The temporal extent for these uniform high and low speed flows are estimated to be roughly withinτIto 4τI, whereτIis the integral time scale of the turbulent flow in our experiment,defined using hydraulic diameter of the channel and mean center line velocity. Based on their scales, these flow patterns are likely to be the footprints of commonly reported streamwise low and high speed streaks in the buffer layers, which yield temporal extents in a similar range [24 , 25] .

Remarkably, our measurements also capture several instances of strong spanwise meandering motions (appearing in around 10%of the data), with spanwise scales on the order of ～2-3δνas illustrated in Fig. 1 e and Supplementary Video 2. Such near-wall meandering “sinuous”motions were reported by Fage and Townend [1] ,which used an ultramicroscope to examine the dust particles moving very near the wall in a water pipe. The location of the observation was at about 0.6% pipe radius away from the wall, likely to be within the sublayer based on their flow parameters. However, very few studies have since provided any further quantification from non-intrusive measurements of these motions within the sublayer.These meandering motions usually occur under low-speed flows deep within the sublayer, and some of these particle trajectories yield high curvatures, indicating strong accelerations (Supplementary Fig. 4). The imprints of these motions on wall shear stresses and flow acceleration will be examined in detail in the following sections. It is worth noting that such meandering motions cannot be resolved by state-of-art DNS simulations, which have “standard”grid resolutions in the streamwise and spanwise directions of 12δνand 5δν, respectively [26] .

Overall, based on our observation, the flow patterns in the viscous sublayer are highly unsteady and spatially variable with dominant movements (both streamwise and spanwise) occurring on the wall-parallel planes. The burst and sweep events that involve strong movement in the streamwise wall-normal planes and are reported broadly in the existing measurements in the buffer layer[27]do not appear to be the dominant structures within the viscous sublayer. This trend is generally consistent with the asymptotic analysis of near-wall flow as the wall is approached [28] .Asy+→ 0 , the wall-normal velocity fluctuation varies as(y+)2while the corresponding streamwise and spanwise values vary asy+resulting in a predominantly wall-parallel flow in the sublayer.Note that this asymptotic analysis holds for statistical quantities and does not preclude the presence of instantaneous motions with steep wall-normal components. Nevertheless, we do not observe such steep wall-normal motions in our data.

3.Mean flow statistics within the viscous sublayer

Based on the measured particle trajectories, the mean velocity profiles and the probability density functions (PDFs) of the streamwise and spanwise wall shear stresses are examined and compared with the DNS using standard grid resolutions. The mean streamwise velocity profile (Supplementary Fig. 5a) shows a clear linear trend, matching both the DNS results as well as the hot-film[4–6] and laser doppler measurements [7 , 8] reported in literature.Correspondingly, the spanwise velocity (Supplementary Fig. 5b)yields zero mean profile, consistent with the DNS predictions. This comparison provides a validation of DFRH techniques for turbulent flow measurements in the viscous sublayer. Moreover, neither of these mean profiles show any dependence on streamwise positions in our measurement regions, as shown in Supplementary Fig. 6,suggesting the spatial variability observed in the flow patterns( Fig. 1 ) is unlikely to be associated with the flow not being fully developed.

Following the same method of DNS, the instantaneous wall shear stress from our experiments ( Fig. 2 ) is calculated using the instantaneous velocity of the tracers deep within the viscous sublayer (i.e.,y+<1). As shown in Fig. 2 a, the PDF of streamwise wall shear stress components show a good agreement with DNS results in the lower range of positive stresses (i.e.,). Remarkably,the experiment measurements deviate substantially from the DNS for higher stress events (i.e.,), corresponding to two times(on average) difference in probability in this range. Similarly, for the PDF of spanwise wall shear stress ( Fig. 2 b), the matching between the experiments and DNS is also observed only for lower stress events (i.e.,) and the deviation occurs for higher stresses (i.e.,) at close to the same level as that for. The discrepancies between the experiments and DNS observed in the wall shear stress PDF are consistent with those in the profiles of streamwise and spanwise velocity fluctuations belowy+= 1 (Supplementary Fig. 5c and 5d), which show an increase of the streamwise and a decrease of the spanwise values compared to DNS. Despite the discrepancies present in the range of high stress events,the skewness values for the streamwise and spanwise wall shear stress measured in our experiments at 1.19, 0.07 are close (in terms of absolute values) to DNS estimates (0.99, -0.01, respectively) indicating a similarity in the overall shape of the distribution. However, the impact of these deviations on the kurtosis are more pronounced, with the experimental streamwise value larger than the DNS prediction (5.39 vs. 4.88), and the corresponding spanwise estimate lower than the DNS value (7.36 vs. 8.92). The smaller difference in the streamwise kurtosis between the experiment and DNS(compared with the spanwise kurtosis) may be attributed to the lack of reverse flow events observed in our experiment, which have been reported to occur at extremely low probabilities ( ～0.02%) in zero pressure gradient boundary layers [12] .

It is worth noting that as with the mean velocity the wall shear stress PDFs show little dependence on streamwise position in our sample volume (Supplementary Fig. 6). Therefore, we attribute these discrepancies to the motions unresolved by DNS, particularly,the small-scale spanwise meandering motions shown in Fig. 1 e.Fig. 2 c and d present the instantaneous streamwise and spanwise wall shear stresses associated with these meandering motions.As the figures show, these meandering motions yield low values of streamwise stresses while relatively high stresses along the spanwise direction. Note that the discrepancies observed between our experiments and DNS only suggest the lack of convergence of DNS (under standard streamwise and spanwise resolutions) to the real flows due to the presence of under-resolved motions. The PDFs of measured stresses being higher or lower than those from DNS do not imply the presence of higher or lower probabilities of large stress events in the experiments in comparison to the resolved events in DNS.

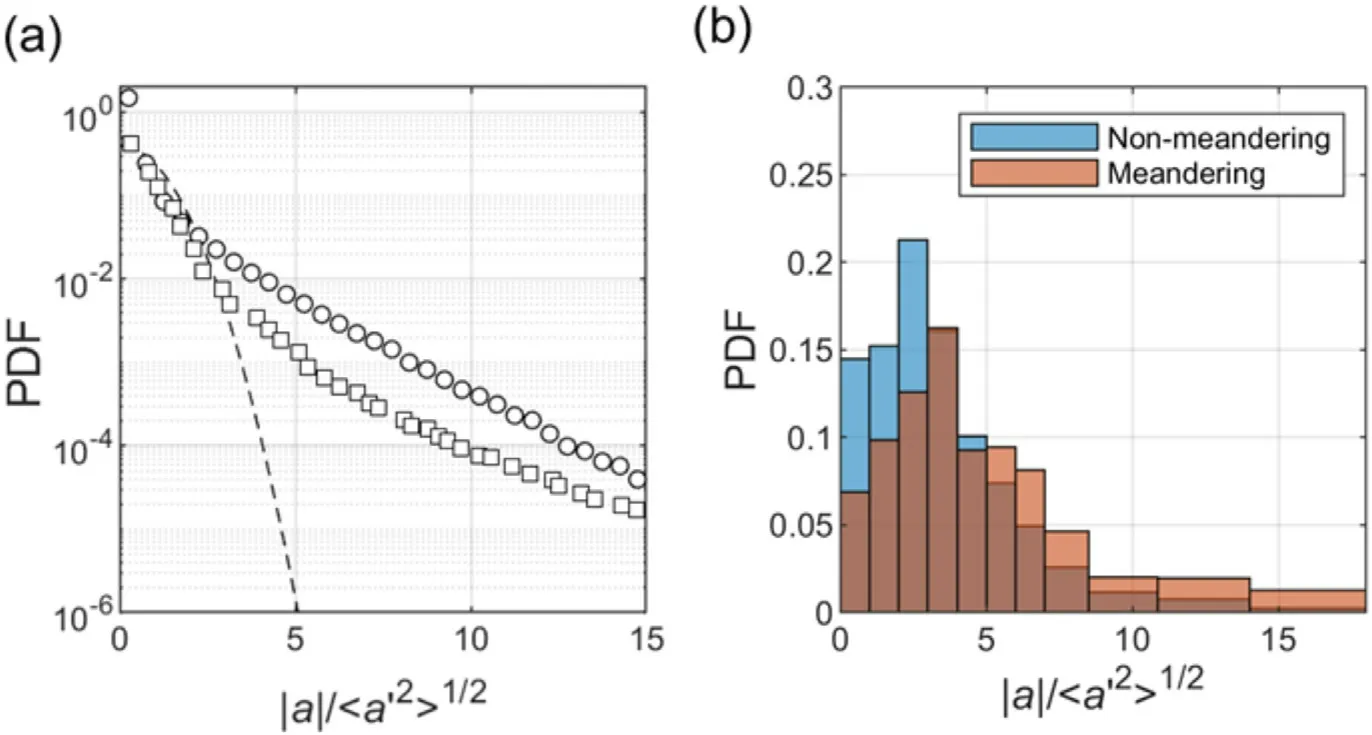
Fig. 3. (a) The probability density function (PDF) of the magnitude of tracer particle acceleration ( ◦) compared to a Gaussian distribution (dashed line) of the same standard deviation and Lagrangian acceleration measurements in isotropic turbulence ( □) reported in Mordant et al . [31] . (b) Comparison of acceleration PDF for meandering vs non-meandering motions, where meandering motions are extracted from the data based on the same conditional sampling used in Fig. 1 e.

4.Lagrangian particle acceleration within the viscous sublayer

To understand the flow intermittency which is at the center of turbulence research [29] in the viscous sublayer, accelerations of tracer particles along their trajectories are examined within the sublayer. Despite the apparent quantitative difference, the PDF of Lagrangian particle acceleration shows some remarkable resemblance with the measurements from isotropic turbulence experiments [30 , 31] . Specifically, they both exhibit a stretched exponential shape with tails extending much higher than a Gaussian distribution of the same standard deviation, which suggests the existence of strong intermittency at small scales in both unbounded and bounded turbulent flows. In isotropic turbulence,such intermittency is known to be a result of uneven breakdown of a mother into two (or more) daughter eddies across the inertial range. Although the exact mechanism that leads to the intermittency in the viscous sublayer is still a research topic,the observation here lends support to the idea of momentum cascade, according to which the momentum flux is carried by wall-attached eddies of various sizes [32 , 33] . Similar to that in an isotropic turbulence, intermittency may naturally arise in the sublayer as a result of the uneven split of the momentum flux from a large-scale eddy to small scale eddies. It is worth noting that like the mean flow statistics, the observed acceleration statistics do not show appreciable dependence on streamwise positions within our sample volume (Supplementary Fig. 7).

We attribute the high accelerations observed in Fig. 3 a to the presence of strong spanwise meandering motions within the sublayer. To illustrate this point, the acceleration PDFs corresponding to non-meandering and meandering motions are compared in Fig. 3 b. Note that the meandering motions are extracted using the same metric implemented for Fig. 1 e and the streamwise velocity for non-meandering motions is sampled to be within the same range as the meandering ones (i.e.,) for an accurate comparison. As the figure shows, the probability of high accelerations for the meandering motions are significantly higher than that for their non-meandering counterparts.

5.Influence of sublayer roughness on macroscopic flow behaviors

The flow structures in the viscous sublayer observed in our smooth-wall experiments can shed light on the impact of sublayerscale roughness on macroscopic flow behaviors. Specifically, the sublayer-scale meandering flows (on the order of ～2-3δνobserved in our experiments) accompanied with strong spanwise acceleration, indicates a significant contribution of spanwise motions to the energy dissipation through the strain rate tensor (Sij). Such spanwise motions are potential sources of instabilities in the flow,which when acted upon by an external stimulus (e.g., adverse pressure gradient) can trigger flow separation, forming a recirculation bubble [3] . Therefore, sublayer-scale roughness can potentially create barriers to reduce the extent of spanwise motions and align flow from spanwise to the streamwise direction ( Fig. 4 a). Such alignment would lead to an increase in the net streamwise flow velocity near the wall, suppressing the flow separation as shown by Evans et al.[14] in a diverging channel section (under adverse pressure gradient) coated with sublayer-scale pillars. Similarly, the presence of roughness in the sublayer may also influence the interaction between sublayer flow and overlaying large-scale turbulence structures, modulating their behaviors, and causing changes in the energy dissipation rate and thus drag on surfaces. In particular, as illustrated in Fig. 4 b and 4 c, the near-wall large scale ( ～100δν)high and low speed streaks may interact with flow in the sublayer and leave signatures as uniformly high and low speed motions in our measurement regions ( Fig. 1 b and 1 c). Correspondingly,sublayer-height roughness with spacing and alignment matching these large-scale streaks can potentially stabilize this interaction and facilitate the momentum exchange between sublayer flow and overlaying turbulence, resulting in an increase in drag ( Fig. 4 b). In contrast, the random arrangement of such roughness may disrupt sublayer signatures of these large-scale structures, destabilizing them and reducing the friction drag accordingly. This hypothesis can explain the behavior of V-groove roughness of ～200δνwidth and ～5δνheight observed in Sirovich and Karlsson [13] , which increases drag when the roughness is aligned with the mean flow but leads to drag reduction when randomly arranged. Nevertheless,further validation of our hypotheses requires direct measurements of flow around these sublayer roughness structures, which we plan to pursue using our DFRH technique in the future.

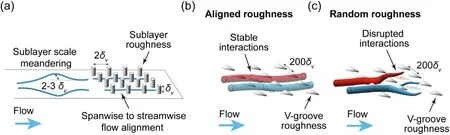
Fig. 4. Schematics showing (a) the possible influence of roughness on sublayer-scale meandering flows in the viscous sublayer through flow alignment and the effects of (b)aligned and (c) randomly arranged V-groove roughness in the viscous sublayer on the potential interaction of sublayer flow with large-scale streaks above.

In the end, based on our sublayer measurement on a smooth wall channel, we would like to comment on the potential limitations of some near-wall measurement techniques, specifically,local seeding employed commonly for near-wall particle tracking velocimetry (PTV) [18 , 20 , 21] . The implementation of such seeding introduces a wall-normal component of velocity associated with the injection of tracer particles. In the literature, the injection speed is limited to a small fraction of centerline velocity in the test section to minimize the influence of local seeding on the near wall flow structures [34] . However, considering the small wall-normal velocity observed in our viscous sublayer measurements, the influence of such method needs to be considered carefully when studying the interaction between the sublayer flow and overlaying turbulence. As another example, shear stress sensors using micropillars, introduced by Brucker et al. [35] and extended for dynamic shear stress in Grosse et al. [36 , 37] , are based on the assumption that the viscous sublayer flow is steady and laminar. The highly unsteady and spatially varying flow patterns observed in our sublayer measurements may cast some doubts on the accuracy of instantaneous shear stress measurements using such sensors in a turbulent near-wall flow. Specifically, their spanwise wall shear stress distribution has a kurtosis of 5.46 [37] , substantially smaller than both our experimental measurements and the DNS prediction.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

Funding for this research was provided by The Office of Naval Research (Grant No. N0 0 0141612755). A large part of the computational work was performed using resources at the Minnesota Supercomputing Institute (MSI) at the University of Minnesota ( http://www.msi.umn.edu ) and the Advanced CyberInfrastructure (ACI)at Penn. State which the authors would also like to thank and acknowledge.

Supplementary materials

Supplementary material associated with this article can be found, in the online version, at doi: 10.1016/j.taml.2021.100239 .