几何不对称对弹塑性射弹入水运动影响数值仿真研究

2021-07-30冯沐桦郭荣君李天雄孙宇新

弹箭与制导学报 2021年3期

冯沐桦，郭荣君，李天雄，孙宇新

(南京理工大学瞬态物理国家重点实验室，南京 210094)

0 引言

随着对海上作战的重视程度越来越高，在海战中扮演重要角色的高速射弹的地位也日益提高。高速射弹跨介质入水过程形成入水空泡[1]，兼有高载荷、非定常以及强瞬时等特性，对武器的弹道特性和结构特性有着很大影响[2]。在射弹入水相关实验方面，Chen等[3]通过实验研究了高速入水弹丸的弹道稳定性，分别确定并量化了弹头形状，入水速度和入水角度对细长弹丸弹道稳定性的影响。结果表明，扁平弹丸产生的峰值压力最大，并且具有理想的弹道稳定性。相比之下，头部形状系数最大的卵形弹丸显示出明显的轨迹不稳定和姿态偏斜。陈先富等[4]在室内靶场对球形和锥头圆柱体两种弹型进行了水平入水实验研究，讨论了不同入水参数对不同弹型弹体入水空泡形态的影响，发现由于入水速度过快(720～1 370 m/s)，而弹体结构强度不足以支持这么高速度的入水冲击，导致弹体破碎，空泡不够稳定，不能得到明显的空泡形态发展规律。施红辉等[5-8]进行了大量不同弹型、不同头型、不同速度的入水实验研究，分析了不同条件下对射弹入水后自由液面的稳定性、空泡形态的影响。根据对实验数据的分析和总结，获得了不同头型的运动体入水规律，并根据该规律提出一种新型有助于射弹入水减阻的方法。

射弹入水转向相关问题涉及多项影响因素，文中主要研究了几何不对称对弹塑性射弹入水运动的影响，利用弹头切削角进行区分，通过分析弹体压力，入水轨迹，射弹俯仰角和速度因素，分析射弹入水转向的受力机理，揭示切削角度对射弹入水运动的影响规律。

1 数值计算模型

1.1 射弹模型

为了研究几何不对称对射弹入水运动的影响，一共设计了4种不同头型的射弹结构，构建模型如图1所示，根据对弹头的切削角度不同，共分为不切(对称射弹)、切削15°、切削18°、切削21°四种头型。在仿真中，弹身长78.5 mm，弹径12.7 mm，网格尺寸大小选取1.5 mm。

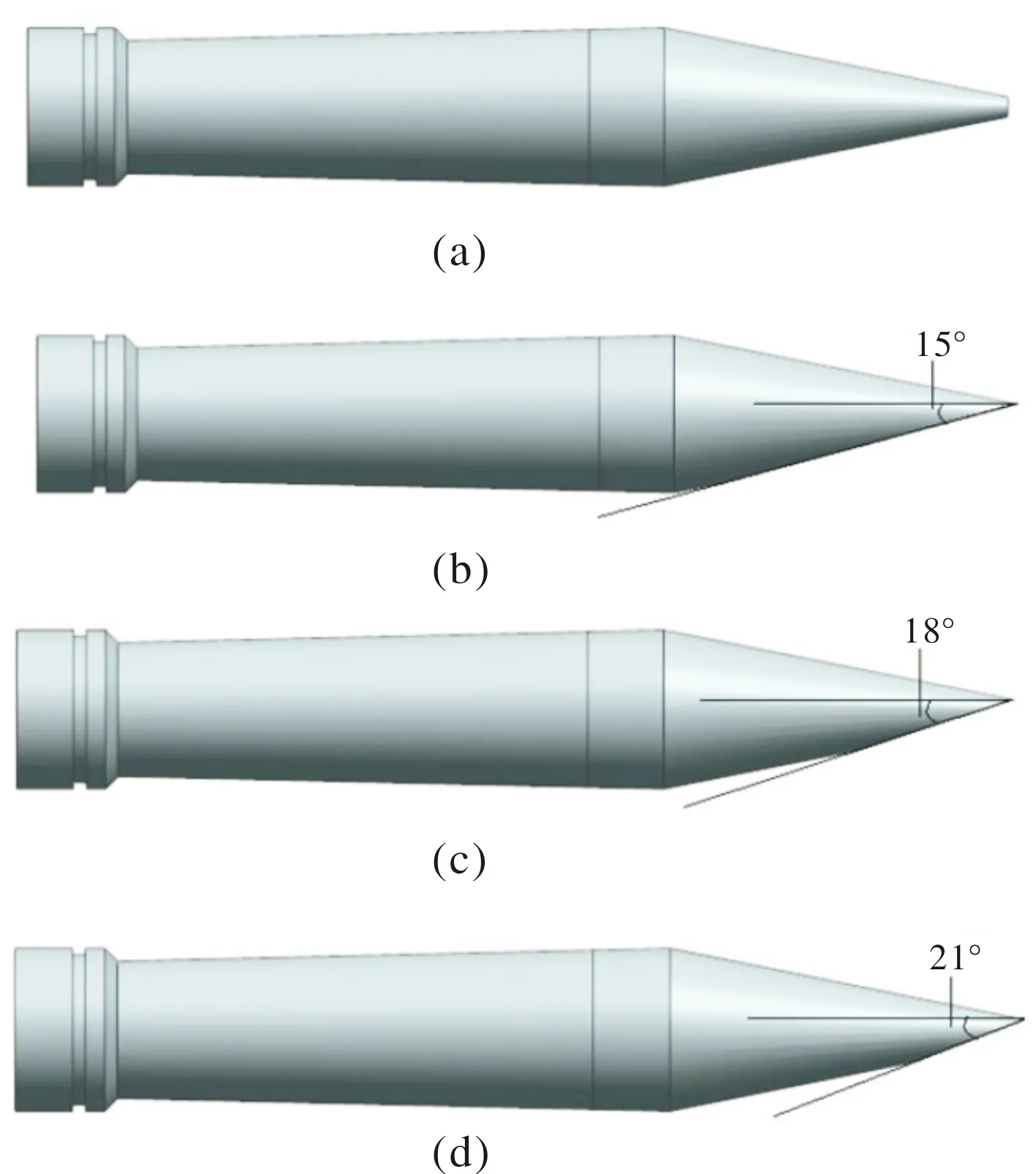
图1 4种不同头型的射弹

1.2 整体计算模型

使用Autodyn软件计算。计算时使用二分之一模型进行计算，如图2所示。为了减小边界效应的影响，水域尺寸设置为800 mm×800 mm×60 mm，网格尺寸大小为1 mm。

图2 计算模型图

1.3 材料模型

整个弹体采用弹塑性材料[9]，以JC强度模型对射弹高速入水转向引起的大变形、高应变率等问题进行模拟。钢材料屈服应力σy可表示为：

σy=[A+B(εP)n](1+Clnε*)[1-(T*)m]

(1)

式中：A为钢材料的屈服强度；B为钢材料的硬化常数；C是钢材料的应变速率敏感度；m是钢材料的热软化指数；n是钢材料的硬化指数；εP是等效塑性应变；ε*是规范化的塑性应变率；温度比值T*是室温Tr和熔化温度Tm的函数，即

(2)

(3)

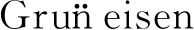
US=C1+S1UP

(4)

钢材料的参数取值如表1所示。水域模型中采用的水的材料参数、多项式状态方程根据压缩状态的不同具有不同的形式。

表1 S-7钢的Johnson-Cook 强度模型参数

当水压缩时(μ>0)，状态方程为：

P=A1μ+A2μ2+A3μ3+(B0+B1μ)ρ0e

(5)

当水膨胀时(μ<0)，状态方程为：

P=T1μ+T2μ2+B0ρ0e

(6)

当水既不压缩也不膨胀时(μ=0)，有：

P=B0ρ0e

(7)

其中P为水中压力，μ为压缩比，μ=ρ/ρ0-1；e为水的内能；ρ0为水密度，取ρ0=1 g/cm3；A1=2.2×106kPa；A2=9.54×106kPa；A3=1.457×107kPa；B0=B1=0.28；T1=2.2×106kPa；T2=0。

1.4 计算工况

数值仿真中，主要讨论几何不对称对射弹入水运动的影响，同时对不对称射弹又由切削角不同进行对比区分，因此弹头切削角共分为不切、15°、18°、21°四种，入水角度为60°，入水速度为400 m/s。现将各种入水条件进行编号，以方便后面区分，具体编号如表2所示。

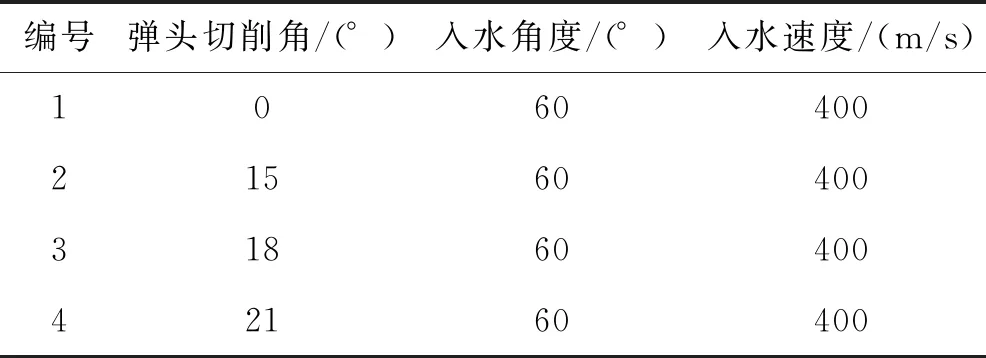
表2 各种入水条件编号表

其中编号1为几何对称射弹，编号2、3、4均为几何不对称射弹。

2 数值计算结果分析

2.1 射弹入水应力分析

选4种射弹入水受力及应力变化进行分析，先是挑选系列切削角下弹的航行初期、航行中期及航行末期受力分析，如图3～图6所示。

图3 1号条件下不同时刻射弹侧面压力云图

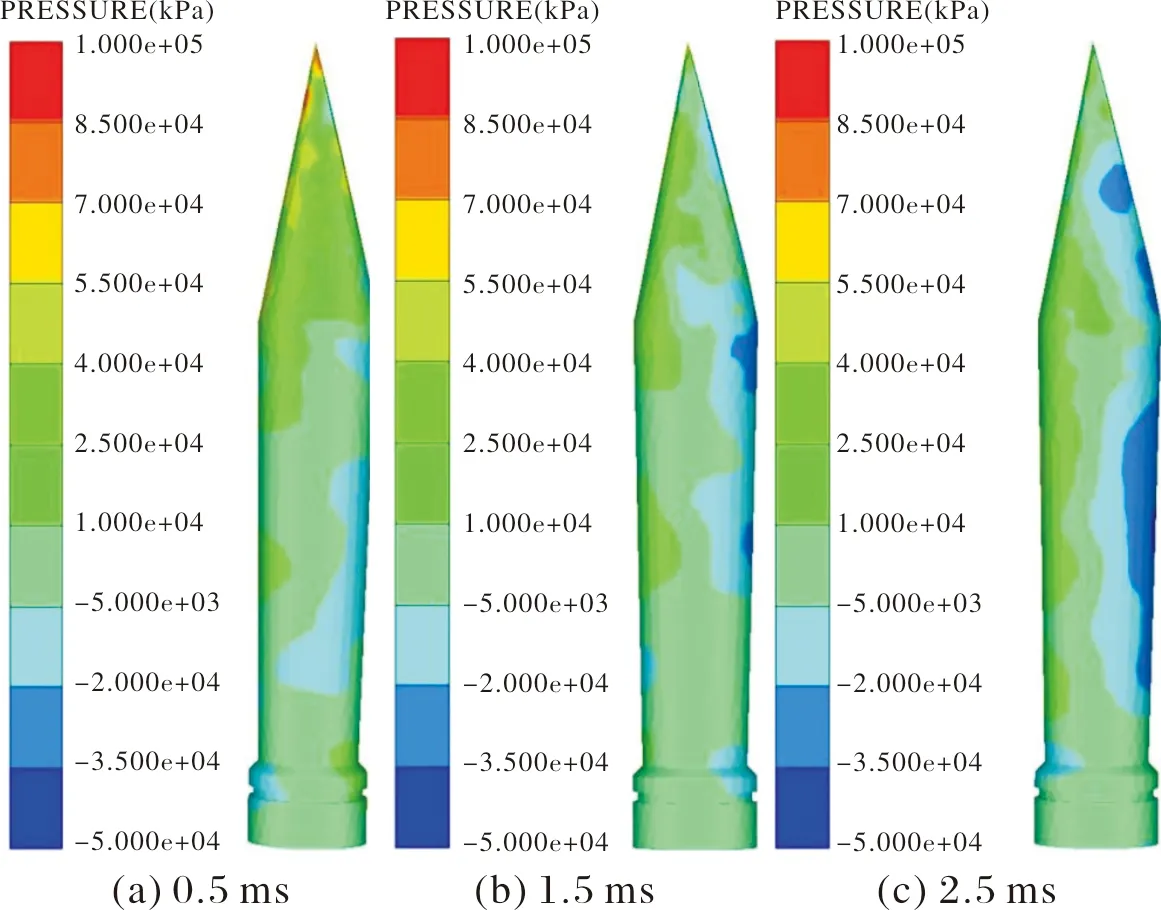
图4 2号条件下不同时刻射弹侧面压力云图

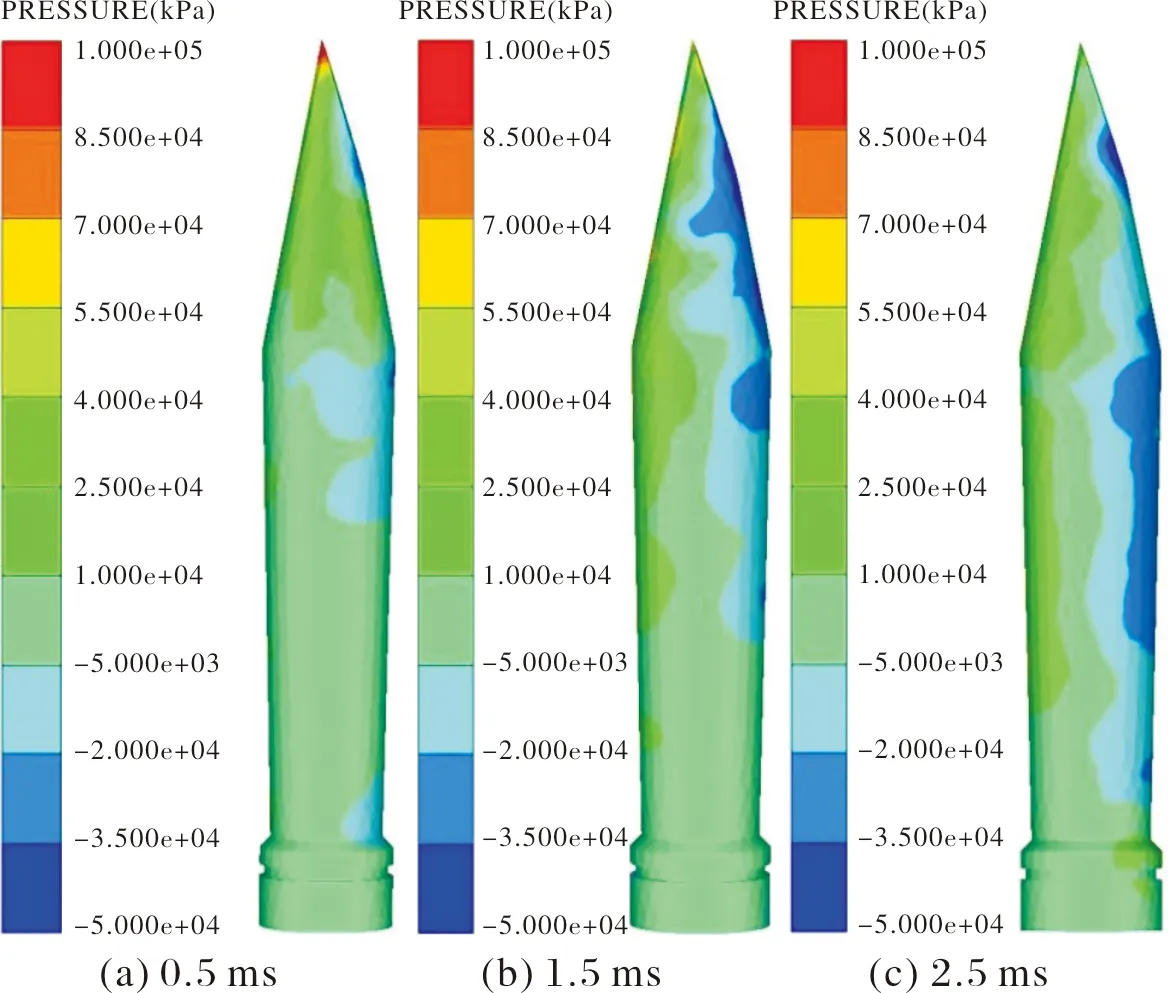
图5 3号条件下不同时刻射弹侧面压力云图

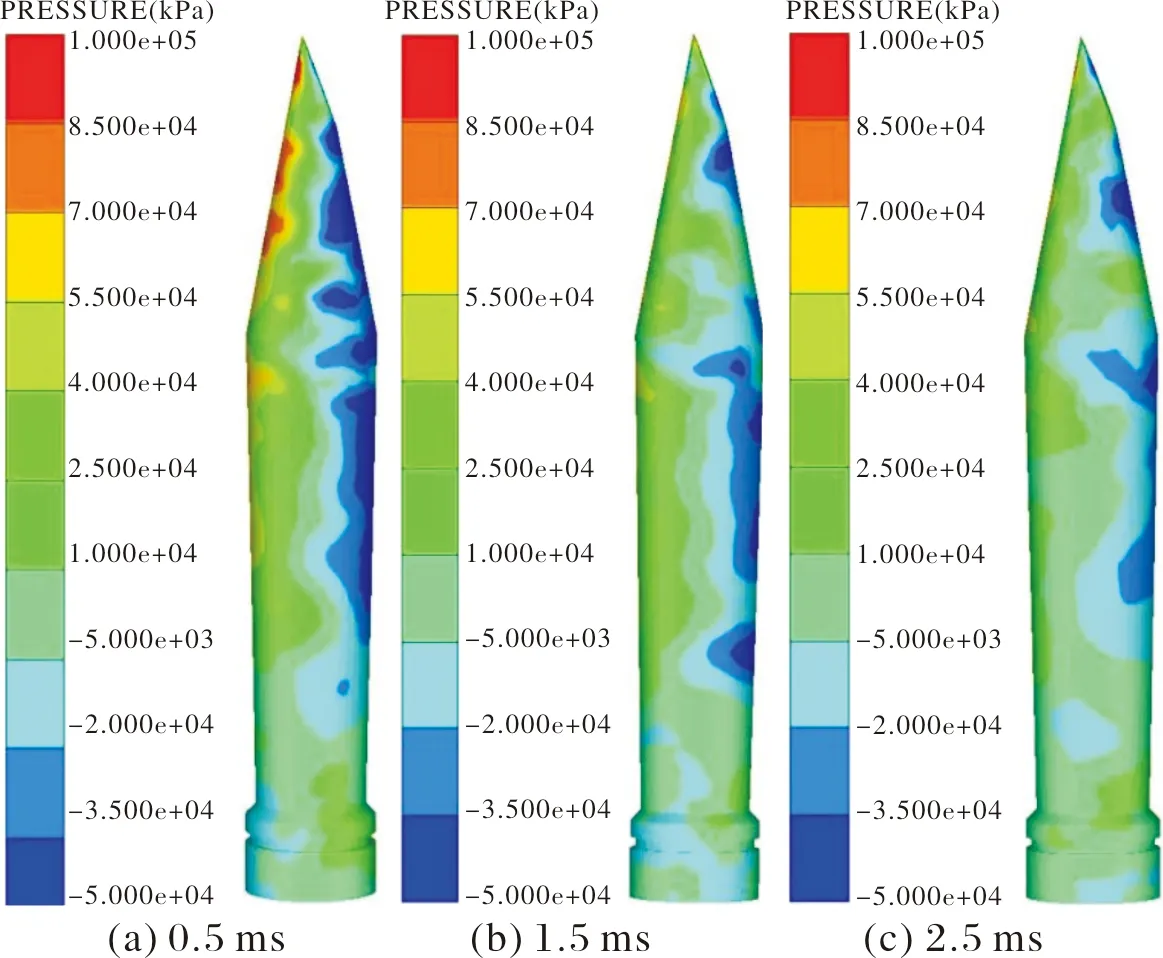
图6 4号条件下不同时刻射弹侧面压力云图

为了方便分析和比较，压力云图范围均为-50～100 MPa，压力略微超过100 MPa以深红色显示，低于-50 MPa以深蓝色表示。且规定图中左侧为弹的上部，右侧为弹的下部。

从云图中可以看出，航行初期(0.5 ms)弹压力主要集中在头部，而射弹中部至尾部受力非常小，主要是因为射弹刚入水时，形成超空泡，射弹后部几乎没有碰到水域，所以头部充当主要的受力部分，而头部切削角不同，也导致头部受力不同，切削角越大，受力的部位越多，进而会影响后面弹的运动轨迹。

因为0.5 ms时弹体运动轨迹相差不大，下面只分析1.5 ms和2.5 ms两个时刻的入水轨迹，如图7～图10所示。

图7 1号条件下不同时刻射弹入水轨迹图

图8 2号条件下不同时刻射弹入水轨迹图

图9 3号条件下不同时刻射弹入水轨迹图

图10 4号条件下不同时刻射弹入水轨迹图

在航行中期时(1.5 ms)压力主要集中在射弹下部，此时由运动轨迹图可以看出，射弹下部基本全部与水域接触，且带切削角的射弹切削角越大，射弹下部沾湿面越大，受力越大，而射弹上部进一步远离水域，射弹上部由于弹体内部的应力以及弹头的受力导致受力略微增大。

在航行后期(2.5 ms)，从弹体的压力云图可看出射弹上部受力随时间推移持续减小，射弹下部压力受力位置有向弹尾移动的趋势，主要是因为随着入水时间的推移，空泡有闭合的趋势，与1.5 ms时刻相比弹尾与水域接触的更彻底，且射弹偏转角度更大，射弹前部受力更小，因此呈现出受力位置向弹尾移动的趋势。同时射弹上部仍不接触水域，主要受力与弹体前部的受力及弹头的应力有关，因此射弹上部受力也更小。

从图3～图6可以看出，切削角为 21°时，射弹受力较大，而且根据入水轨迹分析可以发现切削角较大，射弹偏转较早，则弹体下部较早与水接触，从而导致受到较大压力，因此会使射弹在入水过程中动能损失更大，使得最终弹体在x方向位移更小，在y方向位移更大。从忽扑理论可以判断出会更早发生忽扑现象，有可能对弹道的稳定性产生影响。

2.2 弹头切削角影响分析

主要对相同条件下几何不对称和切削角对射弹入水转向的影响，进行两种入水角度(60°和75°)和两种入水速度(300 m/s和400 m/s)下系列弹头切削角的对比。通过观察不同时刻的状态图可以得出，随着入水时间的增加，射弹运动方向将进行不同程度的偏转，但不同的条件都会对偏转程度造成影响。现针对不同条件的影响及如何影响进行分析。考虑到分析需要获取射弹在水中运动时的速度等各项数据，于是在计算模型上预设3个高斯点(弹头、弹身、弹尾各一个高斯点)进行分析。

2.2.1 通过俯仰角进行分析

从图7～图10可以看出，几何对称的射弹在航行末期已彻底失衡，会在水中翻滚前进直至停下，失去其作用，而带切削角的3种几何不对称射弹发生了4次忽扑现象，且一次比一次现象更不明显，表明其弹道越来越稳定，只要射弹下表面沾湿面积大于上表面，就会持续产生一个变化的力促使射弹进行转向，但随着时间推移，这个力会越来越小，直至空泡闭合。规定俯角初始为正，仰角初始为负，根据不同条件，绘制4种不同条件下的俯仰角曲线如图11所示。

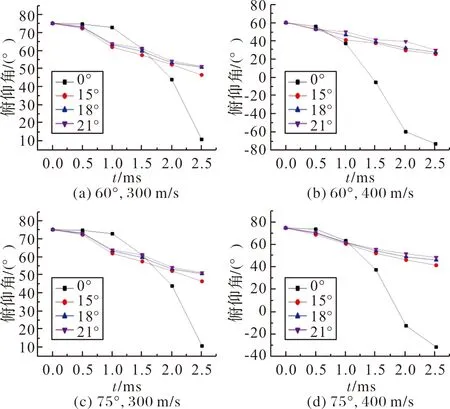
图11 4种条件下不同射弹俯仰角曲线

从4组曲线图可以看出，几何对称的射弹在0.5 ms之前和其他带切削角的射弹俯仰角相差不大，之后在1 ms之后弹道便逐渐失稳，急剧偏转，最终出现仰角为正的情况，由于水域尺寸的限制，数据只取了0～2.5 ms之间，因此出现仰角不为正的曲线。但是总体可以看出，几何不对称射弹入水运动要稳定很多，且切削角越小，转向效果越好，切削角为15°的射弹在相同条件下均要比其他两种切削角的射弹俯角要小5°～6°，表明在相同入水条件下，切削角为15°的射弹在俯仰角的变化上要优于其他两种切削角的射弹，稳定性上远远优于几何对称的射弹。

2.2.2 通过速度进行分析

主要讨论相同条件下系列切削角对射弹总速度的影响。合速度Va曲线图如图12所示。

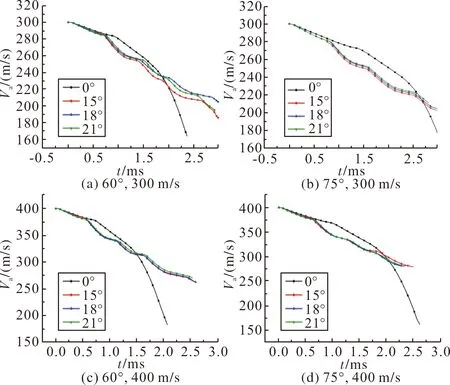
图12 不同入水条件下各切削角射弹的合速度比较曲线图

可以看到0.5 ms之前，也就是第一次忽扑发生之前，4种不同切削角的合速度基本一致，因为这个阶段之前射弹的受力位置都在头部，弹身和弹尾均未与水域接触，此时能影响射弹姿态的条件有限，因此4种射弹基本无差别，第一次速度的快速下降的时间点与第一次忽扑发生时间点基本吻合。由于几何对称的射弹忽扑发生的较晚，因此速度快速下降时间也较其他3种系列切削角的射弹到来的更晚。但由于弹道失去稳定，射弹无法恢复到正常的运动轨迹，几何对称的射弹速度持续快速下降，截至计算终止点时，速度远低于其他3种切削角的射弹。在图中还可以看出，其他3种射弹由于忽扑的发生，合速度不可避免的发生波动，但是都能快速调整姿态，避免速度的过快下降。切削角为15°的射弹在合速度上失去了优势，速度较其他两种射弹均要低一点，根据忽扑现象发生的原理推测，弹头切削角为15°的射弹在弹头沾湿面积上要大于其他两种射弹，导致射弹整体的受力面积加大，射弹受力更大，力矩也更大，因此调整运动姿态需要消耗的能量更多，导致速度较其他两种切削角的射弹略低。