某9 mm 手枪弹侵彻MDF 的弹道特性*

刘子德，王光华，董方栋，崔 斌

（1. 中国兵器工业第208 研究所瞬态冲击技术重点实验室，北京 102202；2. 公安部物证鉴定中心，北京 100038）

在持枪作案、恐怖袭击等案件或事故的调查中，经常需要对现场进行弹道重建[1-2]。而木材是城市中家具制作和建筑结构中的常用材料，弹丸对木材的冲击试验是弹道重建研究中的一种重要技术手段，试验中靶板上留存的弹坑深度或弹头穿透靶板的能量损耗可以对射击位置和射击角度的判定提供依据[3-4]。科研工作者针对装甲毁伤以及防护工作进行过大量的弹丸或破片高速冲击试验[5-8]，木质靶板在侵彻试验中应用较少。木制材料中25 mm 厚松木靶曾被看作人员模拟靶[9]；法医和刑侦人员针对弹道重建进行过一些其他木质材料的侵彻试验，通过记录子弹轨迹，可以使研究人员更好地理解所发生事件的性质和顺序。当前的研究主要集中在临界跳弹角和跳弹或穿孔后弹头的偏斜[10-12]。其中，Kerkhoff 等[10]采用2 种口径的手枪弹对4 种不同密度的木材进行过弹道侵彻试验，研究发现，弹头发生跳弹的临界角度与弹头口径和木材特性相关，并且弹头发生跳弹的临界角度与木材的密度和硬度存在极强的线性关系；Mattijssen 等[13]对石膏板、中密度板和金属板进行了不同角度的侵彻试验，提出根据靶板厚度以及材料特性应选用合适的测量方法，以减小系统误差，提高测量的准确度和精确度，其中探针法、椭圆法和带入法三种测量方法最为常见。考虑到木材中，中密度板（medium density fiberboard, MDF）是一种廉价的建筑材料，广泛应用于家具、橱柜和其他室内建筑。因此，开展手枪弹侵彻MDF 的弹道特性研究可以为涉枪案件的快速侦破提供数据支撑。

本文中以MDF 为研究对象，通过开展不同速度、不同弹着角手枪弹侵彻MDF 的试验，获得弹头侵彻MDF 的深度、弹头入射速度和出射速度等关键信息，并对试验结果进行分析，建立弹头侵彻密度板的数值仿真模型，进一步分析弹头侵入MDF 后的弹道特性。

1 试 验

1.1 试验装置及方法

试验装置由9 mm 弹道枪、不同装药量的9 mm 手枪弹、厚度为25 mm 的MDF 和靶架（靶架角度可调节）组成，其中弹头质量为8 g。试验中通过光幕靶和高速摄影分别获得弹头的入射速度（v1）和出射速度（v2）。试验时靶板距离枪口10 m，手枪弹射击距离较短时（9～18 m），弹道轨迹可看作是一条直线，出枪口到MDF 的距离始终相等，因此每发试验弹着点具有一致性。

1.2 试验数据

表1 为手枪弹侵彻MDF 试验的有效数据，表中：θ 为着靶角度，P1为靶板厚度方向上弹头侵彻密度板的深度，ΔE 为弹头贯穿或者嵌入MDF 状态时弹头损失的能量。

表 1 弹头侵彻中密度纤维板的试验数据Table 1 Tested data of bullet penetrating medium density fiberboard

由表1 可知，弹头正侵彻厚度为25 mm 的MDF 时，穿透状态下，弹头的剩余速度和能量损失量与入射速度均为正相关性；弹头嵌入中密度板时，嵌入深度与入射速度为正相关性。其中入射速度为111、95、92 m/s 时，P1分别为13.8、10.8、9.34 mm；入射速度为56 m/s 和43 m/s 时，密度板表面分别留存3.57 mm和2.42 mm 深度的弹坑。

试验7 中，弹头穿透MDF 后剩余速度为19 m/s，共损失了68.3 J 能量，弹头剩余能量为1.44 J。试验8 中，弹头穿深为13.8 mm，能量损失为49.3 J。这表明，弹头正侵彻25 mm 厚MDF 时极限穿透速度介于111 m/s 和132 m/s 之间，并且更靠近132 m/s。试验19 中，弹头最大侵彻深度为9.72 mm，弹头在密度板表层滑移一段距离后，最终产生跳弹现象。试验20 中，直接产生跳弹现象，密度板表面存在轻微擦痕。这表明，弹头速度降低和着靶角度减小均会引起跳弹现象，弹头着靶角度减小相比速度降低致使跳弹现象发生的概率更大。

部分MDF 受损伤区域如图1 所示：图1(a)中，弹头高速穿透MDF，MDF 背面出现脱落，损伤区域呈圆形，但损伤面积较小；图1(b)中，MDF 背面出现较大区域的隆起和部分脱落的现象，这是由于弹头穿深较大或者刚刚穿透MDF 时，MDF 上出射面弹孔区域承受拉伸作用；图1(c)中，弹头嵌入MDF 的深度为9.34 mm，MDF 背面未见损伤。

图 1 密度板损伤区域Fig. 1 Damage area in medium density fiberboard

弹头正侵彻且穿透MDF 时剩余速度与入射速度拟合曲线和弹头能量损失量与入射速度拟合曲线分别如图2 和图3 所示。

图 2 剩余速度随入射速度的变化Fig. 2 Residual velocity varied with incident velocity

图 3 能量损耗量随入射速度变化Fig. 3 Energy loss varied with incident velocity

由图2 可知，弹头的速度不高于250 m/s 时，速度降接近常数；弹头速度为395 m/s 时，弹头的速度降减小。由图3 可知，弹头正侵彻且穿透25 mm 厚MDF 的情况下，能量消耗量与入射速度表现出线性相关性。经由Origin 软件拟合得出，弹头穿透密度板的情况下，能量损失量与入射速度之间经验公式为：

式中：ΔE 为弹头损失的能量，J；v1为入射速度，m/s。

侵彻力学中，Poncelet 阻力模型[14]应用较广泛，其中侵彻阻力主要基于牛顿第二定律，弹头侵彻木板过程中的侵彻阻力公式为：

式中：m 为弹头质量，v 为特定时刻t 的瞬时速度；F 为t 时刻的侵彻阻力，β 为靶板材料的强度参数，α 为靶板的惯性应力。

由式（2）可推导出弹头侵彻木靶的侵彻深度(P)与弹头的着靶速度v0和特定时刻t 的速度v 之间的关系式为：

当α=0 时，模型称作Robins-Euler 模型，P 与v0之间的关系式为：

在此模型中，弹头的速度降为常数。根据试验中弹头侵彻MDF 的嵌入深度可求得：α=0.012 kg/m，β=3 342 kg·m/s2。因此，弹头侵彻MDF 时，P（m）与弹头侵彻速度之间的关系式为：

根据侵彻阻力公式，弹头的速度较低时，靶板的强度项参数β 占主要优势，这时的惯性项参数往往可以忽略；当弹头的速度较高时，弹头的惯性项参数αv2占主导地位。因此，当弹头最终嵌入密度板时，根据式（4）可知，弹头的能量损耗量与嵌入深度呈线性关系；且弹头低速穿透MDF 时，弹头的速度降为常数。随着弹头速度增大，弹头的惯性项参数相比密度板的强度项参数不可忽略时，弹头的速度降减小。

2 弹头侵彻MDF 的数值模拟

2.1 数值模型与材料参数

选用LS-DYNA 有限元软件开展数值模拟。使用Truegrid 参数化建模构造弹头侵彻MDF 的物理模型。调整参数化中网格的参数即可获得不同状态的物理模型。网格化的物理模型如图4 所示。

弹头由钢芯、铅套、头壳组成，质量为8 g。MDF 与弹头相比刚度较低，侵彻MDF 过程中弹头不会发生变形。因此，数值模型中将弹头各部分视作刚体，材料模型选用*MAT_RIGID来表征。MDF 呈交叉错落结构，结构均匀，各部方向性能基本相同，因此将MDF 视作弹性体，材料模型选用*MAT_ELASTIC 来表征。弹头各个结构以及MDF 的材料参数如表2 所示[15-17]，且MDF 最大失效应力为0.1 GPa。

图 4 网格化后的物理模型Fig. 4 The physical model after meshing

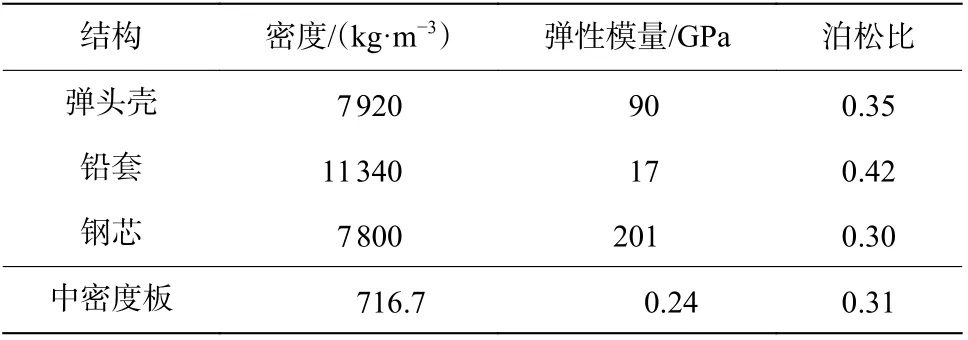
表 2 弹头以及中密度板的材料参数Table 2 Material parameters for bullet and medium density fiberboard

2.2 仿真判据

表3 为弹头侵彻25 mm 厚MDF 时的部分试验与数值计算结果，表中v3为数值模拟中的剩余速度。

表 3 剩余速度试验与数值模拟结果Table 3 Tested and numerically simulated residual velocities

由表3 可知，数值模拟所得剩余速度相比试验所得剩余速度略高。剩余速度的误差在15%以内。当弹着角为30°时，剩余速度的试验值与数值模拟结果之间的误差最小。弹着角为30°，试验中弹头入射孔和出射孔在密度板平面上的水平距离为80 mm，数值模拟中偏转的水平距离为82.6 mm。弹道轨迹如图5 所示。

图 5 试验和数值模拟的弹道轨迹Fig. 5 Tested and numerically simulated ballistic trajectories

2.3 入射速度变化对侵彻过程的影响

弹着角为30°，入射速度分别选定为380、350、300、250 m/s。弹头偏转角度φ 随时间的变化曲线如图6 所示。

由图6 可知，弹头开始侵入MDF 时，均会向着靶角度减小的方向（负方向）偏转。这是由于弹头开始侵入MDF 时，向负方向偏转所受的阻力相比原弹道方向阻力小。随着侵彻深度的增大，弹头向射出中密度板表面的方向偏转相比沿原来侵彻方向所受的侵彻阻力小，此时偏转角度向正方向增大。

弹头侵入中密度板后的负方向偏转角度与着靶的速度呈负相关性。弹头速度为300、350、380 m/s 时，弹头射出中密度板时偏转角度小于2°。弹头速度为250 m/s 时，弹头首先向负方向偏转16.8°，射出中密度板时向正方向偏转6.8°，弹头在中密度板内发生了大角度偏转。这表明，弹头高速穿透中密度板的过程中偏转角度始终较小；弹头低速穿透中密度板时，在侵彻过程中会发生大角度偏转。

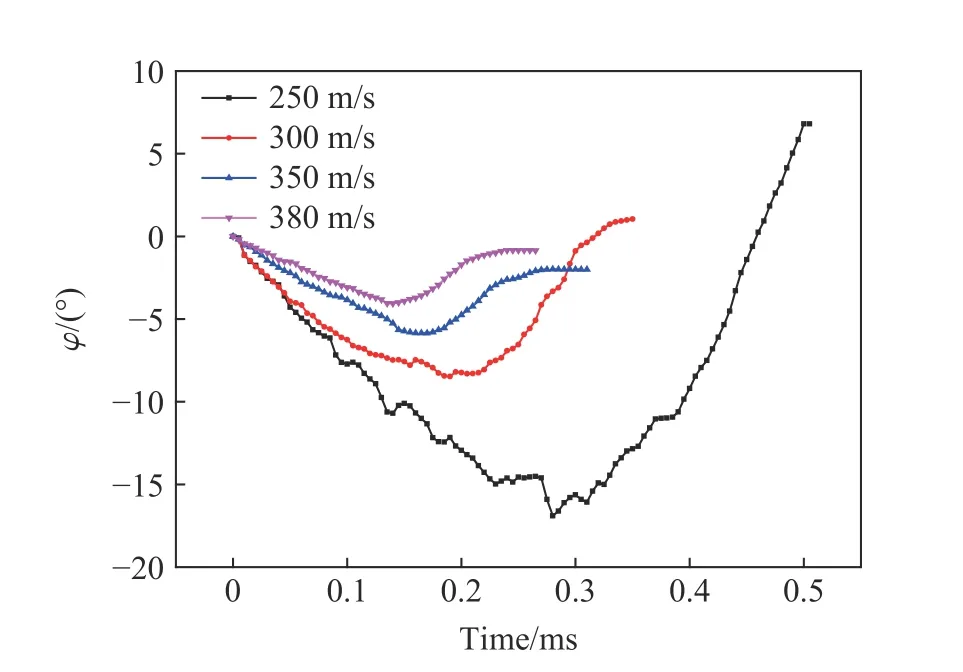
图 6 不同入射速度时偏转角随时间的变化Fig. 6 Change of deflection angle with time at different incident velocities

2.4 弹着角变化对侵彻过程的影响

入射速度为300 m/s，弹着角分别为30°、45°、60°、75°和90°，弹头的剩余速度随弹着角的变化曲线如图7 所示，且弹头侵彻MDF 过程中弹头偏转角度随时间的变化曲线如图8 所示。

图 7 入射速度为300 m/s 时，剩余速度随着靶角的变化Fig. 7 Change of residual velocity with landing angle at the incident velocity of 300 m/s

图 8 入射速度为300 m/s，不同弹着角时偏转角度随时间变化曲线Fig. 8 Change of deflection angle with time at different landing angles in the case of the same incident velocity 300 m/s

由图7 可知，入射速度相同时，剩余速度随着靶角度减小而降低，而弹头速度降逐渐增大。当弹着角在75°～90°之间时，剩余速度变化较小。弹着角在30°～45°时，剩余速度变化最显著。剩余速度随着靶角度变化的曲线整体呈开口向下的半抛物线形状。入射速度为300 m/s 时，弹头剩余速度v3与着靶角度θ 之间的关系式为：

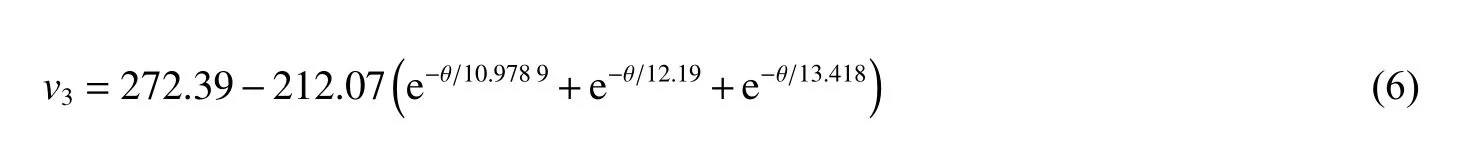
由图8 可知，弹头正侵彻时，弹头侵入MDF 过程中发生小角度偏转，射出MDF 时偏转角度φ 为0°。弹头侵彻过程中负方向偏转角度与弹着角呈负相关性。着靶角度不小于45°时，弹头负方向最大偏转角度为3°，弹着角为30°时，弹头向负方向偏转最大角度为8.5°。5 种工况下弹头射出MDF 时，射出角度均接近原初始着靶角度。这表明，当弹着角小于45°时，弹头侵彻MDF 过程中易发生偏转。

当弹头偏转角度较大时，弹头容易产生跳弹现象。通过数值模型计算了弹头入射速度为370、300、250、200、150 m/s 时发生跳弹的最大弹着角分别为14°、19°、24°、30°、39°。经过Origin 软件拟合可得临界跳弹的着靶角度θ 与着靶的速度v0之间的关系式为：

由此可得，此9 mm 弹头侵彻25 mm 厚MDF 的临界跳弹角为14°。

3 结 论

（3）弹头侵入MDF 时，均会产生向负方向偏转现象；入射速度降低和弹着角减小均会使负方向偏转角增大，弹着角小于45°时，弹头侵彻MDF 过程中更易发生偏转；弹头射出MDF 时出现弹道转正现象。