基于NARX神经网络的火箭炮发火回路状态预测研究
2021-07-30王小召张建新李永保谢立中
王小召,张建新,张 震,李永保,李 锋,谢立中
(湖北江山重工有限责任公司,湖北襄阳 441005)
0 引言
在未来的信息化战争中,保障行动对整个作战体系的支撑作用至关重要。作战方式的多样性对保障的时效性和精确性提出更高的要求[1]。武器装备的智能故障诊断和预测是实现预知维修和自主式保障的重要手段[2]。
神经网络具有极强的非线性映射能力,在故障预测方面受到广泛关注。动态神经网络对过程或工况参数建立动态模型,输出不仅依赖当前的输入,还与当前和过去的输入、输出有关。其中,NARX(nonlinear autoregressive network with exogenous inputs)神经网络性能优越,是非线性动态系统中应用最广泛的一种神经网络[3]。
目前,针对火箭炮状态预测的研究较少,文献[4]采用Elman神经网络针对时间序列的内在特性对防空火箭炮交流伺服系统的速度量进行了预测,但没有考虑其它外在因素的影响。由于服役条件复杂多变,火箭炮状态受环境、振动、冲击等多种因素的影响。基于NARX神经网络引入模糊理论,提出了将多种外部输入的影响因素进行综合评分,以综合评分作为NARX神经网络的外部输入量的预测方法。通过对比分析,该方法能够在保证预测精度满足要求的前提下,使得NARX神经网络的规模减小、收敛速度提高,同时提高了NARX神经网络对火箭炮发火回路状态变化趋势的预测精度。
1 火箭炮发火回路
1.1 关键要素
火箭炮发火系统用于点燃火箭发动机的发火药,将火箭弹按指令要求的顺序和间隔发射出去。
根据收集的历史故障数据对某型火箭炮火控系统故障进行统计分析,结果如图1所示,发火回路故障数量最多,占火控系统总故障数的37.5%。发火回路的主要故障模式为断路、电阻值过高或过低等。

图1 火控系统故障分布
回路电阻主要反映的是发火回路的连接状态,直接关系到火箭炮能否对火箭弹进行可靠发射[5];因此,将回路电阻作为发火回路状态的表征量是合理的。
回路电阻的主要影响因素从两个方面考虑:一方面是介质自身物理特性,除与介质自身的组成有关外,还与所处的环境有关,主要包括温度、湿度等[6];另一方面是接插件的接触电阻,主要受振动强度、振动时间、外力和环境中的温度、湿度、盐雾等的影响。外力是指工作额定载荷之外的破坏力,是不可预知的、偶然的。因此,对于陆军装备某型火箭炮来说,温度、湿度和振动情况是影响回路电阻的主要因素。
1.2 状态数据
在试验室模拟火箭炮工作环境,对发火回路进行不同温度和湿度条件下的振动试验,利用欧姆表检测回路电阻。温度范围为:-40~+50 ℃,相对湿度范围为:20%~95%,取不同温度和湿度的组合共17组,见表1。
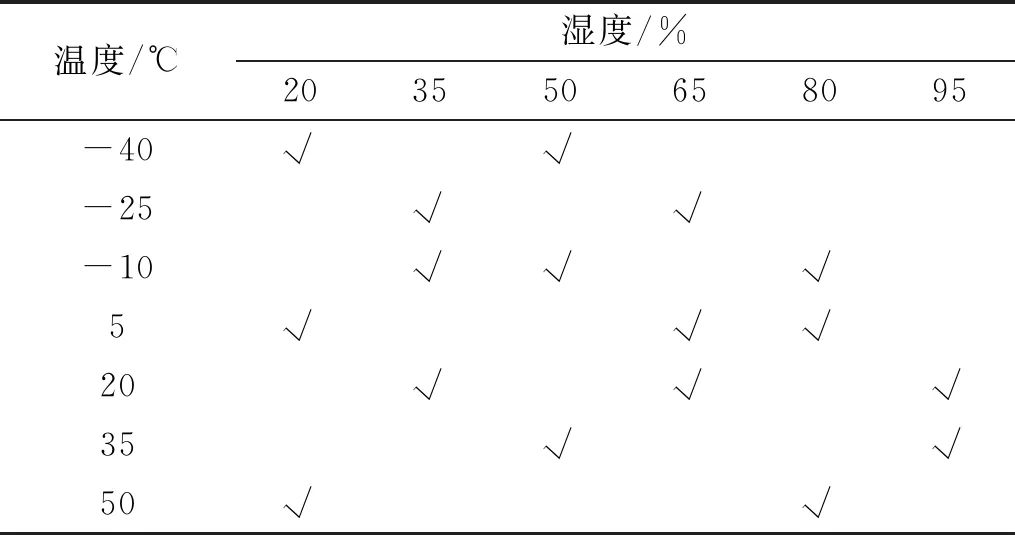
表1 温度和湿度取值表
振动试验在振动试验台上进行,试验量值如图2所示,扫频速度不大于1 oct/min(从5 Hz升至200 Hz再降至5 Hz对数扫频),振动方向为X,Y,Z三个方向,每个方向振动12 min为一个振动周期。
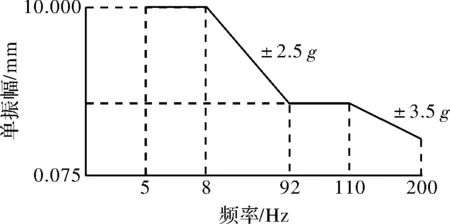
图2 正弦扫描振动试验曲线
试验过程如下:
1)取表1中的一组温度和湿度值,设定试验室温度和湿度;
2)将发火回路放置在试验室4 h;
3)将发火回路放置在振动试验台上,按要求振动3个周期;
4)用欧姆表测量回路电阻;
5)记录温度、湿度、振动时间和回路电阻试验数据。每个振动周期等间隔记录3组数据,每组环境参数记录9组数据。
2 模糊综合评判
2.1 影响因素及权重
发火回路阻值的影响因素集记为U={温度,湿度,振动时间}。采用相对劣化度的分析方法对各影响因素参数进行归一化处理[7],其中温度和振动时间按越小越优型参数处理;湿度按中间型参数处理,参数范围取[20%,95%],最佳运行范围取[50%,70%]。
采用客观赋值法中的相关系数法计算权重[8],形成权重向量A。经对生产过程中试验检测数据的统计分析,对应影响因素温度、湿度和振动时间,权重向量取A=[0.113,0.208,0.679]。
2.2 隶属度
将各因素的优劣状态划分为l1,l2,l3,l4四个评价等级,分别表示优、良、中、差,即等级集L={l1,l2,l3,l4}。选取梯形分布[9]来计算各个因素对各个评价等级的隶属度,形成隶属度矩阵R,隶属度函数曲线如图3所示。
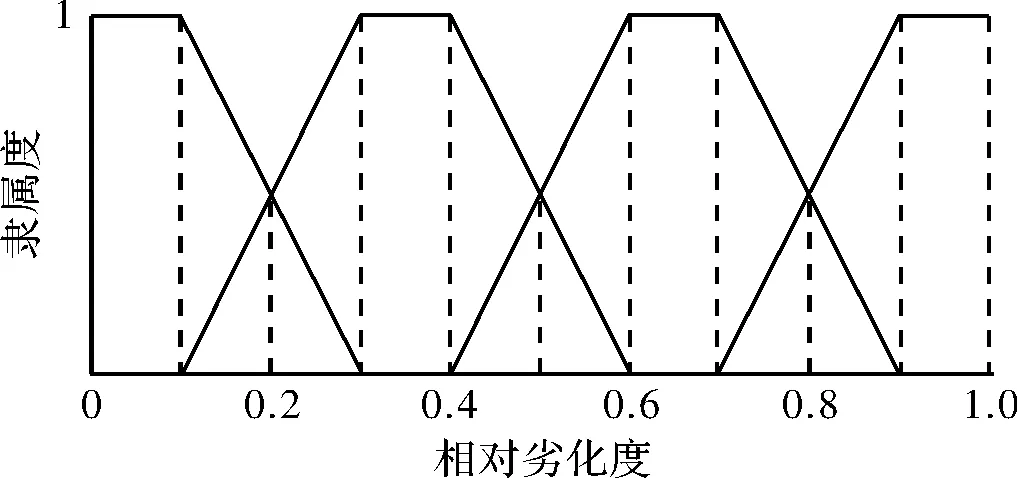
图3 隶属度函数曲线
2.3 模糊综合评判
因素权重向量A和隶属度矩阵R确定后,即可得到综合评价矩阵B:
B=A∘R=[b1,b2,b3,b4]
(1)
其中,“∘”为模糊算子,采用M(·,+)进行运算。
对影响因素进行综合评价的目的是获得各影响因素共同产生的综合影响的量化值。因此,借鉴文献[10]的方法,对等级集L中的每个等级给予一个相应的分值构成分值向量C=[1,4,8,16]。最后,可得到各影响因素的综合评分值:
ε=BCT
(2)
3 NARX神经网络预测模型
3.1 NARX神经网络原理
典型的NARX神经网络结构如图4所示,主要包括输入层、隐含层和输出层,其中输入层含有两个延时环节。
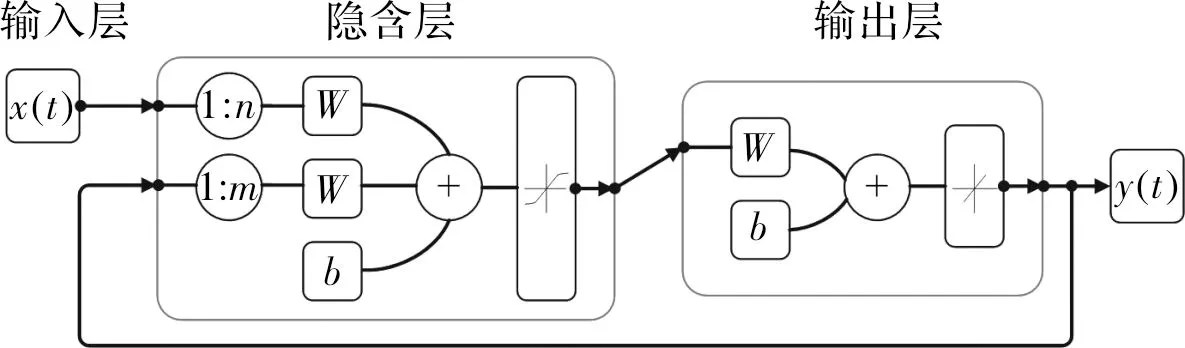
图4 NARX神经网络结构图
在图4中,外部输入变量x(t)的延时长度为n,输出变量y(t)的反馈延时长度为m。一般情况下,输出层只包含一个输出变量y(t),假设外部输入变量x(t)包含多个输入信号xi(t),i=1,2,…,k,则NARX神经网络的数学模型为:
y(t)=f(y(t-1),y(t-2),…,y(t-m),x1(t-1),x1(t-2),…,x1(t-n),…,xk(t-1),xk(t-2),…,xk(t-n))
(3)
与BP静态神经网络相比,NARX神经网络增加了从输出到输入的反馈连接,包含外部输入量和输出量的时间序列,具有丰富的历史信息和优秀的动态性能,能够很好地逼近非线性动力学模型[11]。
3.2 状态预测模型
采用上述模糊综合评判法对每组影响因素进行评判,形成综合评分值序列。建立单输入单输出的NARX神经网络模型A,将综合评分值序列作为外部输入变量,将对应的回路阻值序列作为输出变量。
作为对比,建立三输入单输出的NARX神经网络模型B,将温度、湿度和振动时间3个序列作为外部输入变量,将对应的回路阻值序列作为输出变量。
NARX预测模型的流程图如图5所示。

图5 NARX预测模型流程图
3.3 评价指标
为了评价模型,将预测值yi和实际值hi之间的均方误差(MSE)和相关系数r作为预测精度的评价指标。
MSE表达式为:
(4)
MSE越接近0,说明两个变量的偏差越小,r的表达式为:
(5)
|r|越接近1说明变量之间的线性相关程度越高,为了评价模型的训练速度,将迭代次数作为评价指标。
4 预测分析
4.1 数据处理
为了降低数据量级的影响,提高神经网络的收敛速度,将输入和输出数据归一化至[0,1]范围,数据处理表达式为:
(6)
其中:xi为需要处理的原始数据;xmax和xmin分别为变量x数据中的最大值和最小值。
4.2 参数设置
利用1.2节获得的153组样本数据中的前140组数据对神经网络模型A和模型B进行训练,其中70%作为训练数据,15%作为校验数据,15%作为测试数据。
神经网络模型A和模型B训练算法均采用鲁棒性高且收敛速度快的LM算法。
采用试凑法确定两神经网络模型的隐含节点数和延时长度:首先固定延时长度,然后不断调整隐含节点数,测试不同模型的性能;之后固定隐含节点数,不断改变延时长度[12]。经试验后确定模型A的隐含节点数为4,延时长度为2;模型B的隐含节点数为12,延时长度为2。
4.3 结果及分析
神经网络经过反复训练达到预期要求后,分别利用模型A和模型B对153组样本数据中的后13组数据进行发火回路阻值预测,预测结果如图6和表2所示。

图6 预测结果对比图
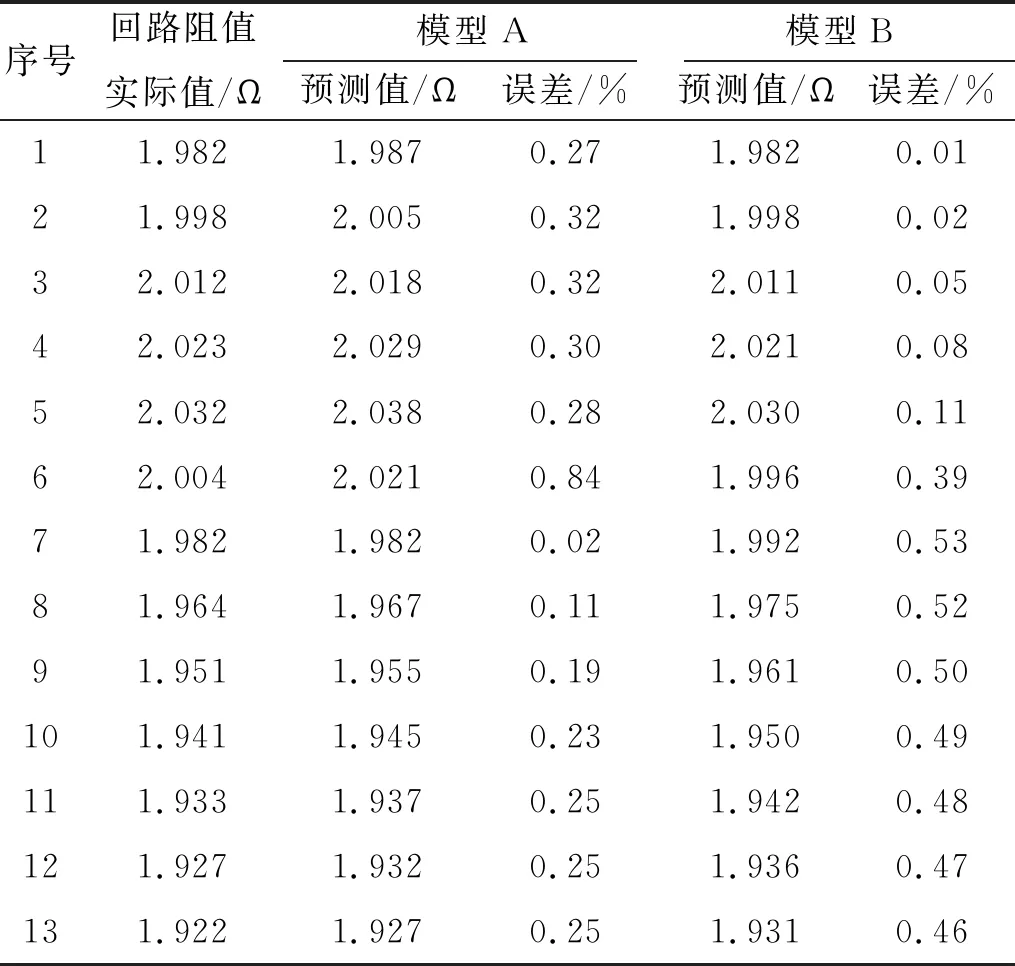
表2 NARX神经网络预测结果表
从单个预测点来看,NARX神经网络对发火回路阻值的预测精度较高,两模型对各点的预测误差均在1%以内。从整体看,模型A和模型B的预测结果和实际值的均方误差分别为4.37×10-5和5.54×10-5,模型A的预测精度略大于模型B;从变化趋势上看,两模型均能较好的预测发火回路阻值的变化趋势,模型A和模型B的预测结果和实际值的相关系数分别为0.996和0.993。由于模糊综合评判对影响因素的影响进行了模糊化,影响因素的综合评分对影响因素变化的敏感度降低,相对于单个影响因素而言变化更加平缓,因而模型A在对发火回路阻值变化趋势的预测上略优于模型B。
为了减小数据划分情况和权重初始值对训练过程及结果的影响,在划分训练数据和初始化权重参数时采用随机的方式,分别对模型A和模型B训练20次,得到均方误差和迭代次数的平均值,见表3。

表3 神经网络评价指标对比表
根据表3,由隐含节点数来看,模型A的规模较小,这是由于对影响因素的模糊综合评判使得外部输入减少,模型得到简化;由均方误差来看,NARX神经网络能够对火箭炮发火回路阻值的训练数据进行拟合且精度均较高,模型A的预测精度略高于模型B;由迭代次数来看,模型A的收敛速度较快。
5 结束语
针对火箭炮服役环境变化剧烈和影响因素复杂等特点,基于NARX神经网络的优良动态性能和非线性拟合能力,引入模糊理论,将模糊综合评判法和NARX神经网络结合,提出了对影响因素进行综合评分后,以综合评分作为NARX动态神经网络的外部输入量,对火箭炮状态进行预测的方法,以某型火箭炮发火回路为例,进行试验对比。结果表明,经过对影响因素的模糊综合评分,NARX神经网络的规模减小且收敛速度更快,对状态变化趋势的预测也更加精确。
