A multi-scale algorithm for dislocation creep at elevated temperatures

Lichao Yuan ,Yujie Wei ,c,*

a State Key Laboratory of Nonlinear Mechanics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China

b School of Future Technology, University of Chinese Academy of Sciences, Beijing 10 0 049, China

c School of Engineering Sciences, University of Chinese Academy of Sciences, Beijing 10 0 049, China

Keywords: Multi-scale algorithm Dislocation glide Dislocation climb High temperature creep Dislocation dynamics

ABSTRACT Dislocation creep at elevated temperatures plays an important role for plastic deformation in crystalline metals.When using traditional discrete dislocation dynamics (DDD) to capture this process,we often need to update the forces on N dislocations involving～N 2 interactions.In this letter,we introduce a multi-scale algorithm to speed up the calculations by dividing a sample of interest into sub-domain grids:dislocations within a characteristic area interact following the conventional way,but their interaction with dislocations in other grids are simplified by lumping all dislocations in another grid as a super one.Such a multi-scale algorithm lowers the computational load to～N1.5 .We employed this algorithm to model dislocation creep in Al-Mg alloy.The simulation leads to a power-law creep rate in consistent with experimental observations.The stress exponent of the power-law creep is a resultant of dislocations climb for～5 and viscous dislocations glide for～3.

One of the significant mechanism of plastic deformation is the collection motion of a large number of line defects in crystal,so-called dislocations.The collection motion especially with climb of dislocations is too long to be accessed by molecular dynamics [ 1 -5 ].Discrete dislocation dynamics (DDD) is then developed and broadly employed to simulate the evolution of dislocation struc-ture and their contribution to plastic strain.Van der Giessen and Needleman [6] proposed a superposition strategy solving a linear elastic boundary value problem,which the boundary conditions vary with the motion of dislocations.Superposition of stress,strain and displacement is conducted between dislocation field and com-pensated elastic field.DDD studies macroscopic response such as Bauschinger effect [7],the effect of loading conditions [8],strain hardening [9] and crack growth [ 10 -13 ] through calculating inter-action and motion at each dislocation in microscopic level.There are two types of interactions.One is short-range interaction,which determines the reaction of dislocations.Another is long-range in-teraction through elastic stress field of dislocations,which mostly determines the collective behavior of the dislocation system [14] .The amount of computation amongNdislocations are on the or-der ofN2.In large systems with more dislocations,it is a greater challenge for the rapid increase of computation load.

When dislocation creep is involved,the computation load is even prohibitive as we often need to examine the dynamics of dis-locations for a long duration of thermally activated process,which is described by a boundary value problem of diffusion equation.Although the boundary conditions of the above problem in Ref.[15] are that of a single infinite straight dislocation,it is precise for low-dislocation densities [16] .Because of their concise and high efficiency,these methods are intensively applied to describe dislo-cation creep [ 17 -21 ].Besides bulk diffusion,dislocations can also climb through pipe diffusion [ 22,23 ].Although the latter has a smaller activation energy and vacancies can spread much faster than that of bulk diffusion,bulk diffusion is the dominant diffusion mode at high temperature and low stress [17] .When materials creep under constant stressσ,the steady-state creep strain rateandσfollow∝σn[ 24 -27 ].Rate-controlling mechanisms includ-ing viscous dislocation glide [28],dislocation pile-up and climbing [ 29,30 ],balance between hardening processes and softening pro-cesses [31],and dislocation networks [32] were proposed to shed light on the physical meaning of the exponentn.In this letter,we aim to report a trans-scale computational method to increase both efficiency and accuracy at the mean time.This algorithm is then applied to dislocation glide and dislocation climb governed creep under constant stress,to reveal the correlation betweennand rate-controlling mechanisms.

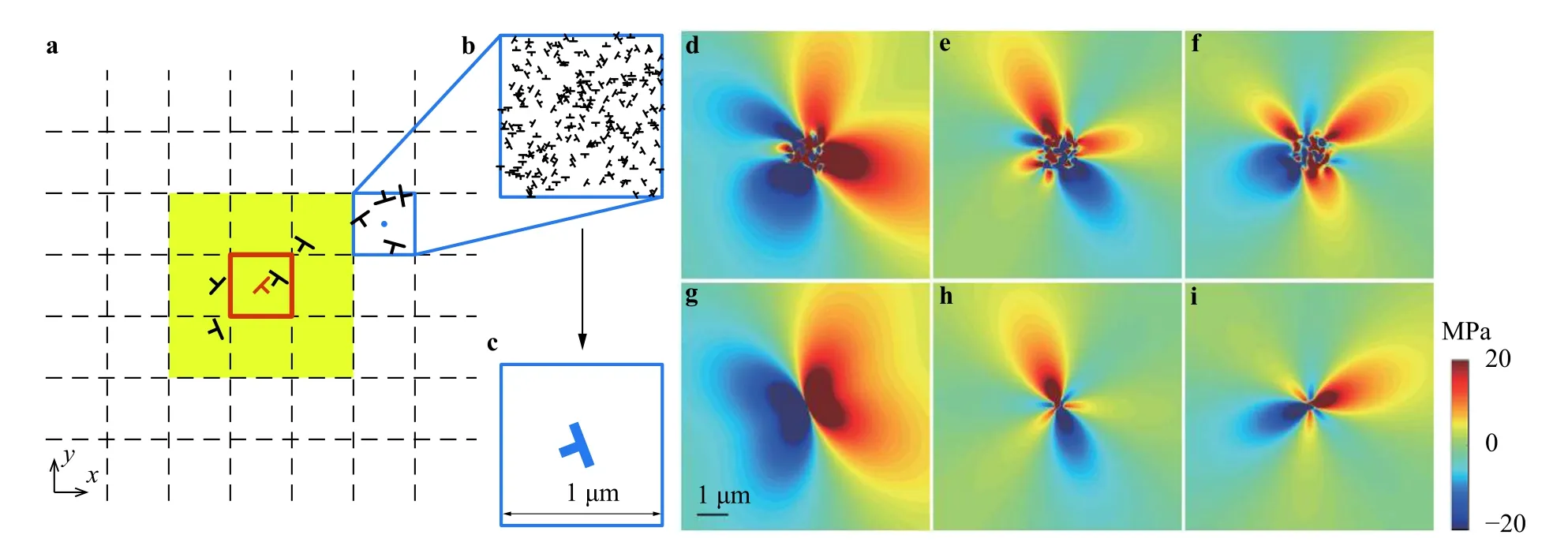
Fig.1. The multi-scale algorithm.a A schematic of the algorithm to show a sample virtually divided into sub-domain grids.b A close-up view of one grid with multiple dislocations,and c the equivalent Burgers vector of b. d -f The stress components σxx, σxy and σyy resulted from all dislocations in the grid shown in b,and g -i the stress components introduced by the equivalent dislocation in c.

The long-range dislocation interaction is accounted for through their elastic fields.New dislocation pairs are generated from Frank-Read sources.In two dimensions,this is mimicked by discrete point sources randomly distributed on discrete slip planes which generate a dislocation dipole with their Burgers vectors aligned with the slip plane direction.This occurs when the magnitude of the Peach-Koehler forcefon source exceeds a critical valueτnucbduring a time periodtnuc,whereτnucis the nucleation stress andbis the Burgers vector.The sign of the dipole is determined by the sign of the resolved shear stress along the slip plane.Annihilation of two opposite signed dislocations on a slip system occurs when they are within a material-dependent critical annihilation distanceLe.Dislocation could glide whenfexceeds the resistance of solute atomτRSSbat a glide velocityvggiven as [33,34]

whereBis the drag coefficient.The magnitude of the climb velocityvcalong the plane perpendicular to the Burgers vector is taken to be related to the normal stress componentσthrough the relation [35]

whereD0is the pre-exponential diffusion constant,Qis the activation energy for vacancy diffusion,kBTthe product of Boltzmann constant and the absolute temperature,andVthe characteristic volume of a vacancy.Obstacles of intersection slip planes or small precipitates to dislocation motion are modeled as points associated with slip planes.Dislocations on the obstacle slip plane get pinned as they try to pass through.Obstacles release pinned dislocations when the Peach-Koehler force on the obstacle exceedsτobsbwhereτobsis a threshold resistance.

For a macroscopic sample in our numerical study,we first divide the sample into small grids,as illustrated in Fig.1a.Forces applied to each dislocation in the central orange grid (see Fig.1a) are treated as following:For a dislocation ‘D’ (the orange dislocation in Fig.1a),its interaction with dislocations in the grid and those in the second-nearest neighbors (the grids in yellow in Fig.1a) are calculated using conventional dislocation pair interaction.For the rest of dislocations in further grids,we simplify their interactions with the dislocation ‘D’ by treating all dislocations in one grid as a super dislocation,as demonstrated in Fig.1c.The super dislocation is located at the center of the grid,and the Burgers vector of the super dislocation is the sum of all the dislocation Burgers vector in the grid.The similarity of stress contour between Fig.1d-1f and Fig.1g-1i implies the rationality of this algorithm.

Fig.2. Exploration about the optimal grid number for the multi-scale algorithm.a Sketch of the single crystal specimen with double slip system for the simple tensile simulation.b The relative computational time as a function of grid number.c The stress error (multi-scale algorithm with respect to the full-scale simulation)versus grid number. d Optimal grid number as a function of total dislocations.

We model a two-dimensional single crystalline Al-2.2 at% Mg alloy with two active dislocation slip systems in a rectangle area of widthW=5 μm and lengthL=15 μm.So far we only consider edge dislocations in the crystallite.The two slip planes form an angleθ=±36.25°with respect tox-axis (see Fig.2a).The slip planes are spacedbapart.A reference material is considered which has Frank-Read sources randomly distributed on these slip planes with a source densityρsrc=20 μm-2.Each source is randomly assigned a nucleation strength,τnuc,which follows a Gaussian distribution of average of 50 MPa and a standard deviation of 15 MPa.The nucleation time for the sourcestnuc is taken to be 10 ns [6].The drag coefficientBfor dislocation glide isB=10-4Pa·s [6,36].The obstacles strength is taken to beτobs=150 MPa and the positions are also randomly assigned on these slip lines with a densityρobs=50 μm-2.The resistanceτRSSof dislocations has an average of 9 MPa and a standard deviation about 2.5 MPa.The material dependent annihilation distance is chosen asLe=6b[6].The activation energy for dislocations to climb in Al-2.2% Mg at 573 K is roughly 150 kJ/mol,which is consistent with the activation energy for vacancy diffusion [25].Its material properties are shown in Table 1.

Table 1 Material properties of Al-Mg taken in the DDD,which are estimated at 573 K.

In order to test the efficiency and possible error of the algorithm,a series of uniaxial tension are simulated.Computation cost is obtained for samples of different dislocation source density from 2.5 to 125 μm-2.In Fig.2b,the computing CPU time in multi-scale algorithm is normalized by the time using conventional algorithm.

From Fig.2b,it is shown that this algorithm can be more efficient with more dislocations.For a fixed number of dislocations,with the increase of grid number,the calculation time decreases first and then increases,implying an optimal grid number.In Fig.2c,increasing the grid number does not lead to a smaller relative error.In our two-scale algorithm,dislocations in the grid and those in the second-nearest neighbors are calculated using conventional dislocation pair interaction,which is precise.When the grid number increases,error from far field grids may be decrease;however,the domain for precise interaction including both the nearest and the second nearest neighbors reduces and the corresponding error increases in contrast to that of bigger grids.The competition of these two gives rise to an optimal grid number.Assuming a homogeneous system with randomly distributed dislocations,for a total number of dislocationsNDand the number of gridsNG,the number of dislocations in the yellow area in Fig.1a is 9ND/NG;the number of super dislocations outside of this region isNG-9.Thus,the number of interactions (calculation load)Sat one simulation step for a single dislocation is roughly estimated as

from which we derive an optimal number of gridsNGogiven as following

In Fig.2d,uniaxial tension results conform to the law of 0.5 power.Substituting Eq.(3b) into Eq.(3a) and the two-scale algorithm can reduces the computation load fromNDtoND0.5.

We first show in Fig.3a stress-strain behavior of uniaxial tensile at room temperature.The dislocation simulation algorithm we introduced before is consistent with conventional dislocation dynamics simulations.After a quasi-elastic deformation,dislocation nucleation,gliding and annihilation in combination lead to a macroscopic yielding in the sample and then apparent strain hardening behavior.With the validity of the method been confirmed,we start to simulate dislocation induced creep where long time span and large number of dislocations are needed and it is prohibitive for traditional dislocation dynamics simulations.The constant applied stress creep simulations,with stresses ranging from 4 to 45 MPa,were carried out to obtain the steady-state creep rate at each stress.We show in Fig.3b the creep behavior of the same sam-ple subject to three constant stresses.The strain-time evolution at different stresses exhibits typical creep characteristics,with an initial increasing of strain in instantaneous response to stress,a rough linear increasing of strain with respect to time is observed.Following the same routine,we abstract creep rate at different stress in Fig.3c.Similar to experimental observations shown in Fig.3d,our simulation suggests that the creep rate at constant stress exhibits three distinct stages,each governed by different dislocation mechanisms.

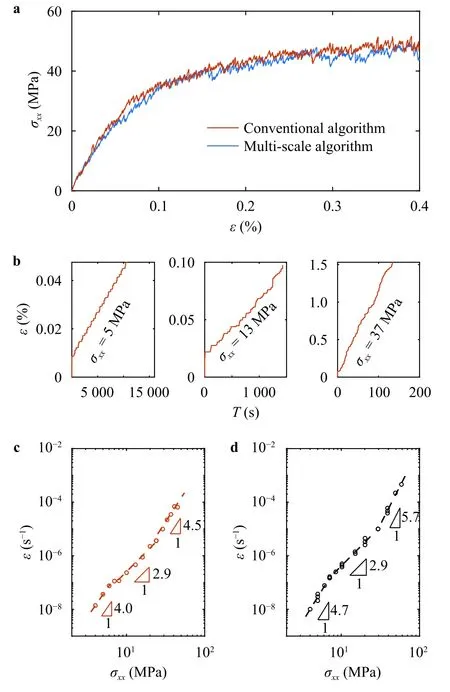
Fig.3. Creep at elevated temperatures (at 573 K) under constant stress.a Stressstrain curves of uniaxial tensile simulations at room temperature.b Evolution of strain as a function of time.Variation of strain rate as a function of nominal stress from c simulation and d experiments for Al-2.2 at% Mg alloy [27,38].

While it is broadly accepted that steady-state creep strain rateandσoften follow∝σn[24-27],different dislocation mechanisms give rise to distinct power law exponentn.From our simulations in Fig.3c,we see a creep-rate versus stress exponent closing to 5 (4 to 7 generally) in the first stage,and it is suggested that creep is controlled by dislocation climb [29,30,40] and can be rationalized by dislocation activities shown in Fig.4a.From the evolution of dislocation density in Fig.4a,the dislocation density of the first stage is dominated by dislocation climb,and leads to a dislocation density proportional toσ3.9.For smallσ,Eq.(2) can be rewritten as

Fig.4. The contribution of different dislocation mechanisms to the total creep rate.a The contribution of dislocation climb and dislocation glide to creep and evolution of the dislocation density.b A dislocation bypasses an obstacle by climbing.c The evolution of creep plastic strain from different dislocation mechanisms under external stress of 37 MPa.d Creep rate as a function of climb rate from 298 K to 773 K at a constant stress of 37 MPa.We normalize the climb rate by that at 573 K (v573).

where climb ratevcvaries linearly with stressσ.According to Orowan equation [41],we have

Now we have a rough estimateσ4.9,which is in agreement with the stress power at the first stage in Fig.3c and 3d.

With increasing stress,dislocation climb contributed deformation drops and dislocation gliding starts to take over,and nownis about 3 in Fig.3c and 3d,which is generally believed to be the result of dislocation viscous glide constrained by solute atoms [28].

At higher stresses (see Fig.4c),while the creep strain from direct dislocation climbεcis rather small compared with the total creep strainεt,the creep strainεc -g from gliding of unpinned dislocation due to climbing is prominent.The creep stainεg from dislocation gliding alone also increases as a result of newly generated dislocations.As dislocation climb facilitates pinned dislocations to overcome the high gliding resistance on the original path,it actually now becomes the controlling mechanism at high stress levels,as illustrated in Fig.4b.

In general,the creep rate may be approximated as

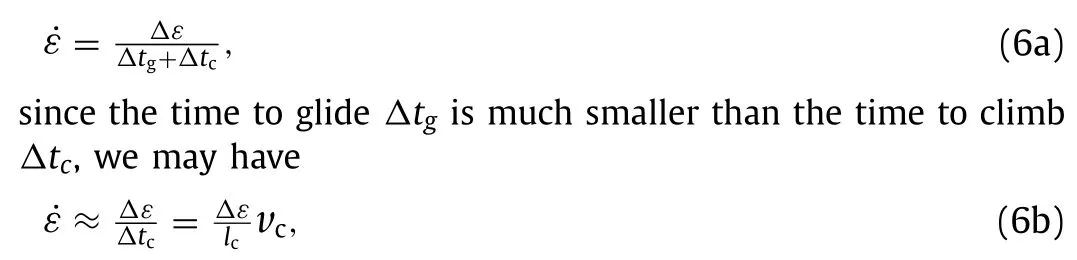
wherelcis a characteristic length to climb (see Fig.4b).Indeed,we see a linear relationship between the creep rate and the climb rate at high stress levels (in Fig.4d),implying climb being the governed mechanism for creep.

To summarize,given the distinct role played by dislocation creep at elevated temperatures in crystalline metals,it is of significance to apply a high fidelity modeling strategy to capture this deformation behavior.When using traditional discrete dislocation dynamics (DDD),those calculations are usually of long duration and high cost:we often need to update the forces onNdislocations involving～N2interactions at each time step.In this letter,a multiscale algorithm is proposed to calculate the interaction between dislocations more efficiently through super-dislocation in macroscale and conventional approach in micro-scale,and the formula of optimal grid number is given depending on number of dislocations,which leads to a computation load of～N1.5.The good agreement between the calculated and measured power-law creep exponents is a result of well captured underlying physics of climb and viscous glide.We note,however,that a 2D treatment of dislocation dynamics sets restrictions on (1) the actual degrees of freedom that flexible dislocations have,(2) the incorporation of other dislocation activities such as cross-slip,and (3) dislocation-surface interactions.It is also interesting to study the stress exponents in polycrystalline system;compared with single crystal,the interaction between dislocations located in different grains would be more complex.

DeclarationofCompetingInterest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors acknowledge support from the National Key Research and Development Program of China (Grant 2017YFB0202800),the National Natural Science Foundation of China,Basic Science Center for“Multiscale Problems in Nonlinear Mechanics”(Grant 11988102),the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant XDB22020200),and the Chinese Academy of Sciences Center for Excellence in Complex System Mechanics.