Rotational dynamics of bottom-heavy rods in turbulence from experiments and numerical simulations

Linfeng Jing ,Cheng Wng ,Shung Liu ,Cho Sun , , ,Enrico Clzvrini c,

a Center for Combustion Energy, Key Laboratory for Thermal Science and Power Engineering of Ministry of Education, Department of Energy and Power Engineering, Tsinghua University, Beijing 10 0 084, China

b Department of Engineering Mechanics, School of Aerospace Engineering, Tsinghua University, Beijing 10 0 084, China

c Université de Lille, ULR 7512 Unité de Mécanique de Lille - Joseph Boussinesq (UML), F 590 0 0 Lille, France

Keywords: Particle-laden flows Turbulent flows Direct numerical simulations Particle tracking

ABSTRACT We successfully perform the three-dimensional tracking in a turbulent fluid flow of small axisymmetrical particles that are neutrally-buoyant and bottom-heavy,i.e.,they have a non-homogeneous mass distribu-tion along their symmetry axis.We experimentally show how a tiny mass inhomogeneity can affect the particle orientation along the preferred vertical direction and modify its tumbling rate.The experiment is complemented by a series of simulations based on realistic Navier-Stokes turbulence and on a point-like particle model that is capable to explore the full range of parameter space characterized by the gravi-tational torque stability number and by the particle aspect ratio.We propose a theoretical perturbative prediction valid in the high bottom-heaviness regime that agrees well with the observed preferential ori-entation and tumbling rate of the particles.We also show that the heavy-tail shape of the probability distribution function of the tumbling rate is weakly affected by the bottom-heaviness of the particles.

Many turbulent natural and artificial fluid flows are seeded with small inclusions either organic or mineral or manufactured,called dispersed phase.As examples one can mention the water droplets,the ice crystals,the sand grains or the volcanic ashes car-ried by atmospheric winds;the wide variety of planktonic organ-isms transported by the oceans [1] ;and in the industry the liq-uids loaded in cellulose fibers in paper making production [2] or the tiny bubbles rising in column chemical reactors.Although the common aspect of all these examples is that they concern the fluid transport of small-in-size inclusions (from now on dubbed parti-cles),each case differs by the specific nature of the particles and by their physical properties.The particles shape can be regular like a sphere or irregular,their material structure can be rigid or de-formable,the mass density can be lighter/heavier than the sur-rounding fluid,and homogeneous or not.For what concerns liv-ing particles they can react to external stimuli (like temperature,light or local acceleration and deformations) through motility or changes in orientation or shape.

In the last two decades a vast amount of work has been de-voted to the investigation of the dynamics of particles in turbu-lent flows [3-8] .This renewed interest into a classical fluid dy-namics problem has notably taken a fundamental point of view,considering idealized turbulent flows with their known universal features and simplified models for the particles,often assumed tiny and spherical.Major advances have been performed thanks to the strategy of combining experiments,numerical simulations and theoretical predictions built on models of developed turbu-lence [9] .More recently the studies have attacked the problems of less idealized,real so to say,particles,such as non spherical ones [10] or active particles [11-13] .Researches on the rotational motion of spherical and non-spherical particles [14-27] have re-vealed how the complex dynamics of the turbulent velocity gradi-ent in the vicinity of the particle affects the characteristic tumbling and spinning rates.The rotation of larger particles have been con-nected to the property of turbulence in the so-called inertial range [16,28,29] .Studies of particle dynamics in wall-bounded flow have provided new insights on the fact that particles tumbling proper-ties can be affected by the background shear-flow in a non trivial way [ 25,30,31] .

When particles are non-homogeneous in their mass density dis-tribution,an extra torque induced by the gravitational field comes into play which can affect the preferred orientation and rotation of the particle.This has been revealed to be particularly important in the biological domain for tiny motile plankton,leading to the phenomenon called gyro-taxis or gravi-taxis.This phenomenon first proposed by Kessler [32] is responsible for plankton clustering at small scale by turbulence,and has been the subject of recent important works [33,34].However,the experimental studies of nonhomogeneous active particles by means of living organism are delicate because of their sensitivity to diverse environmental factors and for the unavoidable variability present in any real population.It is clear that experiments with real microorganisms are not the ideal setting to test dynamical models for e.g.non-homogeneous non-spherical particles.

In this paper,we study the statistical properties of the orientation and rotation of passive bottom-heavy neutrally buoyant rod-like particles in developed turbulence by means of dedicated experiments and simulations.On one hand this is a challenging experimental task,because of the many control parameters involved and the high accuracy required for the measurements.On the other hand the availability of simplified model system allows for a numerical study of the system that can be checked against experiments.We will show that this combined approach is capable to assess the predictive potential of currently adopted models for the Lagrangian dynamics of single bottom-heavy anisotropic particles and to reveal the main trends as a function of the control parameters.

We carry out the experiments in the central region (referred as bulk) of a Rayleigh-Bénard convection (RBC) cell in turbulent flow conditions.The RBC system we consider is cubic with sideH=24 cm,while the bulk is chosen as a cube at its center of sizeH/3.The latter choice,already adopted in our previous work [25] is motivated by the fact that we have verified that in that region the small scale properties of the turbulent flows share a strong similarity with the ones found in homogeneous and isotropic flows.A detailed description of the experimental setup can be found in Ref.[25].Here,we carefully match the density of the working liquid (a solution of 15% in weight glycerol in water at a mean temperatureTm=40°C) to the one of the tracked particles so that the particles results to be on average neutrally buoyant in the fluid.The experiments are conducted at Rayleigh numberRa=βgΔTH3/(νκ)=1.4 ×1010and Prandtl numberPr=ν/κ=13 (hereβis the thermal expansion coefficient,gis the gravity acceleration intensity,ΔTthe bottom-top temperature difference,κthe thermal diffusivity,νthe fluid viscosity).The global energy dissipation rate in the system is evaluated from the relation∈=RaPr-2(Nu-1)ν3/H4[35],while the local energy dissipation in the bulk is estimated by considering the ratio of the local energy dissipation rate to global energy dissipation rate via matching with numerical simulations as done in Ref.[25].Thus,the dissipative length and time scales in bulk are,respectively,η=0.94 mm andτη=0.87 s,the Taylor microcale measuresλ=17.6 mm and the integral scaleL=38.2 mm.The resulting Taylor-Reynolds number isReλ≈37.

The bottom-heavy particles are fabricated by threading a polyamide rod into a thin polyethylene ring.The diameter and length of rod ared=0.56 mm andl=10 mm respectively,which results in an aspect ratioα=l/d⋍18.The ring has an inner diameter of 0.56 mm and outer diameter 0.96 mm and a length of 1 mm.The centroid of the ring is placed at the position 0.5 mm away from the centroid of the rod,see particle picture in Fig.1a.Given the basic geometry of the assembled particle,the position of its baricenter can be easily estimated.We estimate ash=0.14 mm the off-center displacement of the particle centroid with respect to the particle geometrical center.

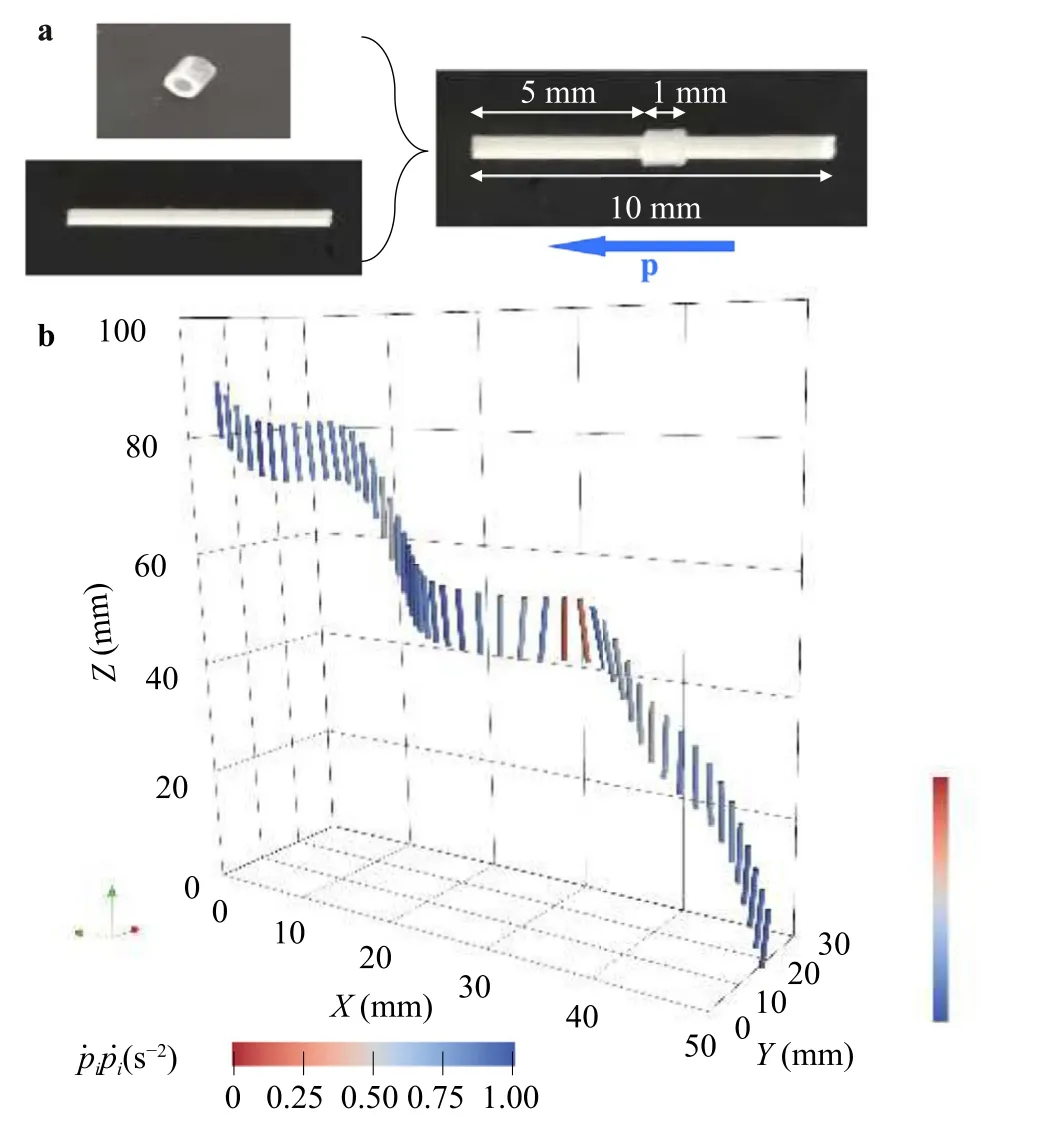
Fig.1. a Photos and scales in mm of one of the axisymmetric bottom-heavy rods and its assembly parts used in the experiments.The orientation of the unit vector p is also shown.b Example of trajectory of a bottom-heavy rod reconstructed via 3D-PTV.The temporal duration of this trajectory is 23 s.The color encodes the quadratic tumbling rate.

The particles are tracked using a three-dimensional particle tracking velocimetry (3D-PTV) technique by means of two orthogonally positioned cameras.The details of the tracking method are the same as in Ref.[25].We track simultaneously～20 particles.Given the volume of the convective cell they can be considered as highly diluted and non-interacting.The recorded series can be as long as a minute,which is in the order of the large eddy turnover time of the flow.A reconstructed trajectory for a typical case is shown in Fig.1b.

The rotation of particles is governed by the dimensionless stability numberψ=B/τηwhereBis a reorientation time scale due to gravity,which is defined asB=να⊥/(2hg).Here,α⊥is the dimensionless resistance coefficient for rotation,same as in Ref.[36],which is ⋍207 in our experiments.We note that due to slight differences in the particles,a precise evaluation ofhand so ofBis arduous.For this reason we also evaluateBin an alternative way,by the direct measurement of the tumbling trajectory in a quiescent flow.In such case the exact evolution of the vertical component of particle orientationpzcan be obtained analytically by solving the equation of motion (5):

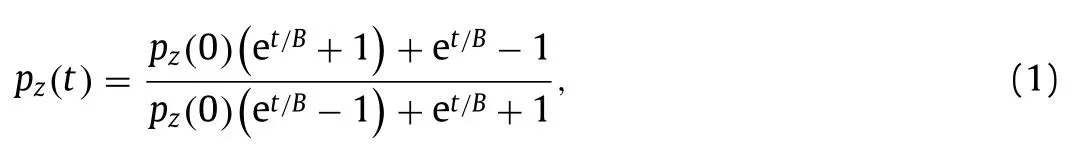
wherepz(0)is a predefined initial condition,that can be easily controlled in the experiment.We proceed as follow,the particle is released in a bottom-up position in the still fluid,its trajectory filmed and the parameterBdeduced from the matching with Eq.(1).With this procedure we estimateψ=0.52±0.1,in good agreement with the a priori estimation of B.

We carry out numerical simulations based on an Eulerian-Lagrangian modelization of the physical problem.This means that the turbulent environment is described by means of direct numerical simulations (DNS) of incompressible Navier-Stokes equations while the particles are described by a point-particle model that takes into account the movement of the center of mass and the spatial orientation of the particle.The equation for the fluids reads as follows:

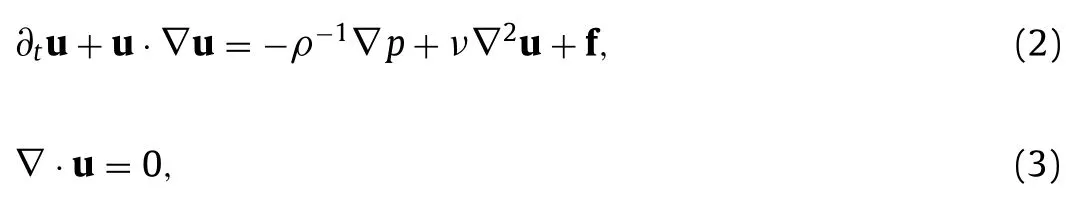
whereu(x,t)denotes the fluid velocity vector field,pis the hydrodynamic pressure,and parameters are the kinematic viscosityν,the reference liquid densityρ.The vectorfrefers to an external large-scale random force with constant global energy input which produces and sustains a statistically homogeneous and isotropic turbulent (HIT) flow.Periodic boundary conditions are enforced along all the directions of the three-dimensional cubic simulation domain.The HIT flow can be characterized by a single dimensionless control parameter the Taylor-Reynolds numberReλ=urmsλ/νwhereurmsis the single-component root-mean-square velocity andis the Taylor micro-scale of turbulence.We simulate an HIT flow atReλ≈32 on a regular grid of 1283nodes.

The model for the Lagrangian evolution of a single particle position,r(t),and orientation,p(t),is described by the following equations:

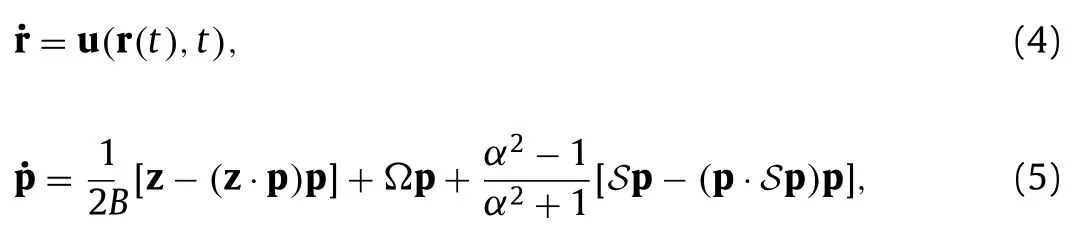
wherepis a unit vector oriented along the particle symmetry axis,and pointing in the direction of its light-top;zis a unit vector pointing upward (i.e.opposite to the gravity direction),S=(∇u+∇uT)/2 andΩ=(∇u-∇uT)/2 respectively represent the symmetric and anti-symmetric components of the fluid velocity gradient tensor at the particle position,∇u.The equation of rotation Eq.(5) is an extension of the Jeffery equation [37] which considers the gravity torque due to the center of mass offset in the particle,as proposed by Pedley and Kessler [36].This model has been originally proposed in the context of motile algae studies and since then extensively used to study the dynamics of gyrotactic swimmers [13,34].This model is appropriate for particles whose motion is ruled by hydrodynamics in the viscous regime.It applies to turbulent flows as long as the particle size and the particle translation and rotation response times are of the order of the respective dissipative (i.e.Kolmogorov) scales.Although here we havel⋍10η,the response times areO(～0.1)τηwhich provide still a reasonable condition for the applicability of the model.This is also supported by previous studies of finite-sized homogeneous fibers in turbulent flows [16,23].The simulated HIT flow is seeded by a large amount of non-interacting particles (～106),divided into distinct families characterized by aspect ratio and stability number parameters varying in the rangeα∈[0.01,100]andψ∈[0.01,100].The simulations are performed with the CH4-project code [38].

We begin discussing the effect of preferential orientation along the vertical direction of the particles,which appears to be a dominant effect in the experimental setting as it can be noticed in the reconstructed trajectory of Fig.1b.This can be quantified by the absolute value of the vertical component of the particle orientation vector |pz|.We use the absolute value here in order to allow for the comparison between experimental measurements and simulations,in fact the experimental trajectory reconstruction technique allows to detect the particle direction but not to resolve its orientation,due to the tiny asymmetry of its body.The probability density function (PDF) of |pz| is expected to be non-uniform in the range [0,1].This is illustrated in Fig.2a which reports the experimental measurement for the rod-like particle with aspect-ratioα=18 and stability numberψ=0.5.In the same figure we show the results of simulations for the same parameters,which are in reasonable quantitative agreement with the experiment.For comparison we also provide the case for high stability numberψ=100,where the particle orientation is only weakly affected by the gravity,and the distribution appears essentially flat.

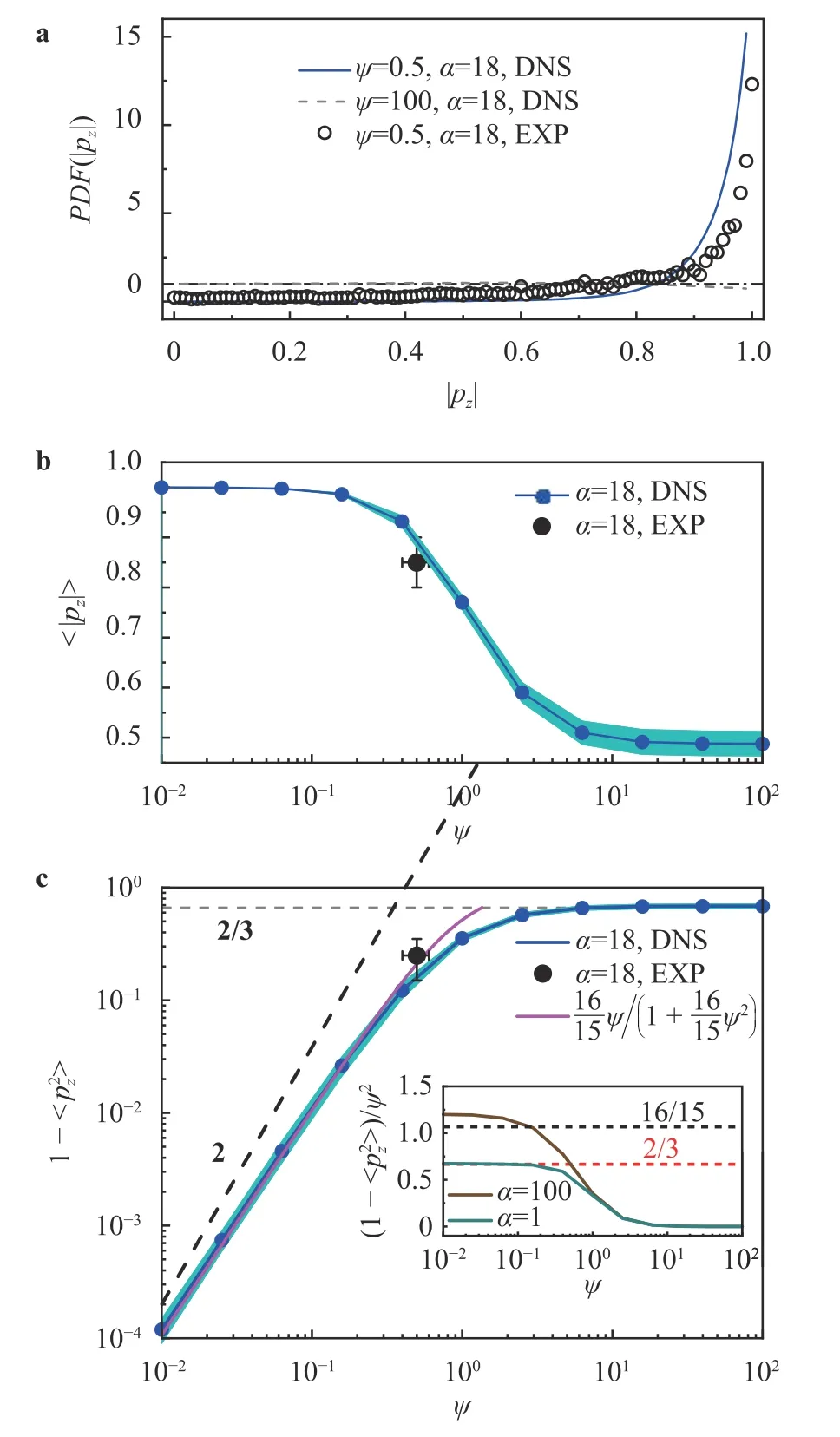
Fig.2. a PDFs of absolute value of particle vertical orientation component|p z|from experiments (EXP) and simulations (DNS).The black dot-dashed line represents the PDF of randomly oriented particles.b Mean absolute value of particle vertical orientation component 〈|p z|〉 as a function of stability number ψ from experiments(EXP) and simulations (DNS).The light blue shaded area represents the error of 〈|p z|〉 in simulations.c 1-〈p2z〉 as a function of ψ in log-log scale.The pink solid line shows the prediction Eq.(10).Inset shows 1-〈p2z〉 compensated by ψ2 as a function of ψ and the expected values according to the perturbative predictions Eqs.(8) and (9).

The trajectory and ensemble (i.e.particle population) average for the same quantity,as a function of the stability numberψis shown in Fig.2b).Such a quantity,as illustrated by the DNS results,monotonically decreases asψincreases from a gravity torque dominated regime(ψ≪1)to the turbulence dominated regime(ψ≫1).The valueψ～1 identifies an intermediate state between the two limiting behaviours (here 〈|pz|〉～)mean-ing 45°angle with respect to the vertical),confirming that the dissipative time-scale of turbulenceτηis the appropriate scale for the description of the dynamics of a tiny particle in turbulence.It also appears that a plateau is reached in the two limits whenThe experimental measurement agrees with the simulations and show a strong alignment with the vertical;converting the observable to an average angle in degrees one finds:acos

In the limit of small but non-vanishingB,a perturbative solution of Eq.(5) up to the first order inBcan be performed.We consider the Taylor expansion of the solutionparound the pointB=0:p(t)⋍p0(t)+Bp1(t)+O(B2),and substitute it into Eq.(5).The equation is then solved order by order inBstarting by the leading order.This leads to

Such predictions are compared with the measurements in Fig.2c,where it is clearly seen the quadratic trend for 1-～ψ2forψ＜1 and the saturation 1-=2/3 occurring in the regime dominated by turbulent fluctuationsψ≫1.The predictions for thin rods Eqs.(9) and (10) compare well both with the DNS and experimental results.The agreement on the scaling prefactor,which is excellent in the case of the sphere,is compared in the inset of Fig.2c.

We now focus on the tumbling rate of the particle,i.e.on its rotation rate in the direction orthogonal to the symmetry axis.Previous studies have shown that the particle shape is responsible for a phenomenon of preferential alignment of rod-like particles with the fluid vorticity leading for prolate particles to a reduced tumbling rate with respect to the spherical particle case and the opposite for oblate particles [14,15,28].We show here how the gravitational torque further reduces the tumbling of the particles.

The PDFs of tumbling rate squared for differentψare shown in Fig.3a.The long tail of PDF of tumbling rate has also been observed for homogeneous axi-symmetric particles [15,16,25].This denotes the presence of intense local rotation rates with respect to the average value 〈〉.The PDF from experiments agrees with the PDF from simulation up to about～10 standard deviations.The differences observed for the higher tumbling rate regime could be a signature of sub-leading inertial effects associated to the finitesize of the particles,as observed in Ref.[16] for homogeneous fibers.Furthermore,a weak stability number dependence is observed on the tail of PDFs,with an increasing intermittency for lowψ;such an observation can be considered as preliminary and will deserve further checks at different Reynolds numbers.

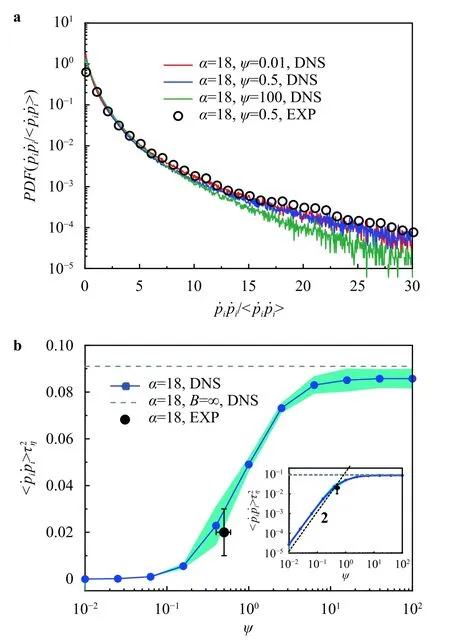
Fig.3. a PDFs of tumbling rate squared from experiments (EXP) (circles) and simulations (DNS) (full lines).b Normalized mean tumbling rate squared 〈〉 as a function of stability number ψ from EXP and DNS.The light blue shaded area represents the statistical error of 〈〉 in simulations.gray dashed line refers to the value of mean tumbling rate squared for homogeneous rod with a similar aspect ratio at Re λ=32.The inset show the same data on a log-log scale,the ψ2 behavior is shown as black dashed line.

The quadratic tumbling rate normalized by the temporal dissipative scale,forα=18 particles at varying the stability numberψis reported in Fig.3b.We observe a marked suppression of the tumbling rate for the particle in the experiments to about 20% of the known value for a corresponding equal-in-shape and homogeneous particle.The numerics suggest that the trend of tumbling as a function ofψis similar to the one already observed for the orientation,with apparent saturation forψoutside the range [0.1,10].The perturbative solution Eq.(6) when derived with respect to time and averaged gives,for spheres (α=1):

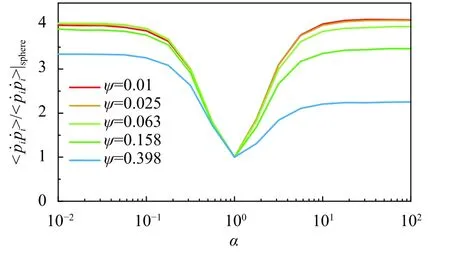
Fig.4. The ratio of mean squared tumbling rate of non-spherical particles with respect to the sphere case,〈〉/〈 〉sphere [Note:same as in the notation on the y axis of the figure],at various stability number ψ in the limit of highly stabilized particles (ψ →0).

Finally,we address the behavior of the mean quadratic tumbling rate in the full two-dimensional parameter space(α,ψ).This can be conveniently done by means of the simulations.The results are illustrated in Fig.5.At largeψvalues,the mean tumbling rate shows two plateaus for slender rods and thin disks,which agrees with the rotation dynamics of homogeneous particles in turbulence (ψ=∞) and with our previous experimental measurements atψ=∞andα=6 and 1/6 in the same bulk of RBC setting [25].As the stability parameter decreases,one observes a more pronounced similarity between disk-like and rod-like particles.And,as already remarked in Fig.4 in that limit the tumbling both of rods and thin disks is larger than the one of corresponding spheres,in agreement with the expectation from the perturbative prediction.

Fig.5. Normalized mean tumbling rate squared 〈〉 as a function of stabil-ity number ψ and aspect ratio in EXP and DNS.The color represents the value of 〈 〉 .The black circle denotes the data from the present experiments.The black square shows the result for homogeneous particles (ψ=∞) of aspect ratio α=6 and 1/6 in the RBC bulk at a comparable turbulent intensity,from Ref.[25].

In summary,we presented a study of the statistics of orientation and rotation of anisotropic bottom-heavy particles in a turbulent flow by means of experiments and simulations.The effect of gravity induced torque due to the inhomogeneity of particles,characterized by stability numberψ,significantly modifies the statistics of the particle orientation and its rotation intensity.At lowψ,the particles are brought to align with the gravity direction.It is found that in this limit 1-and mean tumbling rate squaredscale asψ2at smallψ.A prediction based on perturbation theory shows excellent agreement with the DNS measurements.Our results point to the fact that particulate matter with geometrical and mass density properties that are different from the idealized homogeneous one,are likely to possess rotational properties that are very different from the one indicated by the homogeneous particle model.As we show here even a tiny mass bottomheaviness stabilizes the particle and drastically reduce its tumbling.Further studies will be needed in future to better understand the rich rotational dynamics of non-ideal particles in turbulent flows.In particular it would be of great interest to extend the present investigation to the analysis of spinning rates (i.e.the rotations around the symmetry axis),to the examination of inertial effects for larger particles and ultimately to a the exploration of much more particle shape types and mass-density asymmetries.

DeclarationofCompetingInterest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant 11988102).