A study on equivalence of nonlinear energy dissipation between first-order computational homogenization (FOCH) and re duce d-order homogenization (ROH) methods

Jiajia Yue ,Zifeng Yuan ,c,*

a Center for Applied Physics and Technology, Peking University, Beijing 100871, China

b Department of Mechanics and Engineering Science, Peking University, Beijing 100871, China

c Beijing Innovation Center for Engineering Science and Advanced Technology, Peking University, Beijing 100871, China

Keywords: Multiscale First-order computational homogenization (FOCH) Reduced-order homogenization (ROH) Energy dissipation Computational certification

ABSTRACT Nowadays,studies on the mechanism of macro-scopic nonlinear behavior of materials by accumulation of micro-scopic degradation are attracting more attention from researchers.Among numerous approaches,multiscale methods have been proved as powerful and practical approaches in predicting macro-scopic material status by averaging and homogenizing physical information from associated micro-scopic mate-rial behavior.Usually in mechanical problem,the stress,consistent material modulus,and possible mate-rial state variables are quantities in interest through the upscaling process.However,the energy-related quantities are not studied much.Some initiative work has been done in the early year including but not limited to the Hill-Mandel condition in multiscale framework,which gives that the macro-scopic elastic strain energy density can be computed by volumetric averaging of that in the micro-scale.However,in the nonlinear analysis,the energy dissipation is an important quantity to measure the degradation status.In this manuscript,two typical multiscale methods,the first-order computational homogenization (FOCH) and reduced-order homogenization (ROH),are adopted to numerically analyze a fiber-reinforced compos-ite material with capability in material nonlinearity.With numerical experiments,it can be shown that energy dissipation is the same for both approaches.

Recently,composite materials are widely used in modern and advanced industries,like aerospace engineering,due to light weight,high stiffness,and high fracture toughness.With complex micro-scopic structure and significant differences in material be-havior among micro-scopic constituents,classic numerical tools designed for homogeneous materials can not be used directly to predict macro-scopic phenomenons.Various multiscale approaches then are introduced in the recent two decades,which focus on ho-mogenizing micro-scopic kinetic information to macro-scopic.Ac-cordingly,various macro-scopic nonlinear material behaviors can be explained by micro-scopic evolution.

Hierarchical multiscale methods [ 1,2 ] are employed in simu-lation of composite material with different spatial scales,aiming to transfer kinematic measurement from macro-to micro-scale,and obtain kinetic measurements from an equilibrium state at the micro-scale.Among those methods,a number of methodolo-gies adopt detailed precise discretization of micro-scopic struc-ture,or unit cell in general.For example,the FE2 method uses fi-nite element method for both macro-and micro-scales [3-5] .An-other group of methods try to accelerate the computational pro-cess by putting proper assumptions at the micro-scale.The so-called cluster-based analysis of heterogeneous material is one typ-ical approach [ 6,7 ],where the micro-scopic structure is discretized into several clusters so that the number of micro-scopic internal state variables is significantly reduced.

In this manuscript,two hierarchical multiscale methods are se-lected and compared.One is the so-called first-order computa-tional homogenization (FOCH) and one is named as reduced-order homogenization (ROH) [8],stemmed from the so-called transfor-mation field analysis (TFA) method [ 9,10 ].In Ref.[8],both FOCH and ROH methods are able to predict comprehensive nonlinear behavior.However,it is difficult to prove rigorous equivalency of FOCH and ROH methods,under general material nonlinear behav-iors.It is straightforward for the users to see details of various ma-terial internal state variables at selected material integration point in FOCH method.For example,plastic strain tensor (or the equivalent plastic strain) can be visualized while classic plastic material is assigned to one phase at micro-scale.Damage state variable,which could be treated as approximation of micro-scopic crack,can be observed at corresponding material constituent when material softening occurs.Namely,when a huge computational cost in FOCH is spent for a multiscale problem,the FOCH method is able to provide material status in micro-scale with high resolution.

The ROH method assumes piecewise constant distribution of mechanical quantities (strain,stress,and state variables) over one partition so that computational cost can be reduced compared to FOCH method.It is simple to compare the quantities which can be averaged over one partition or whole unit cell.For example,one can compute averaged strain at all elements within one partition in FOCH approach,and compare it with corresponding constant strain value in ROH method.However,it is not trivial to claim that those two approaches are able to obtain the same energy quantities,like strain energy and nonlinear energy dissipation.In history,the equivalency of elastic strain energy in the linear problem is proved mathematically,namely,the HILL-MANDEL condition.As we applied the ROH approach for mostly nonlinear problem,it is meaningful to study the equivalency of nonlinear energy dissipation.In this manuscript,a numerical study of energy equivalency between FOCH and ROH methods is proposed,including the comparison of elastic strain energy and also the plastic energy dissipation.

A brief review of mathematical background of both FOCH and ROH methods is introduced.The FOCH and ROH methods stem from the strong form,including equilibrium equation,geometry equation,and constitutive equation [11]:

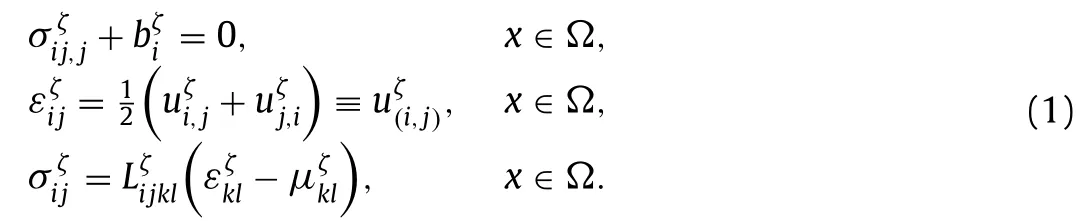
Hereσij,εij,anduiare the field variables denoting stress tensor,strain tensor,and displacement vector,respectively.Lijklis a fourth-order tensor representing linear elastic coefficient,with major and minor symmetry conditions.All the quantities with superscriptζare the field quantities defined in composite domain.denotes eigenstrain tensor which origins from material nonlinearity.For example,the strain-stress relationship for elastoplastic material can be written as

whereis the plastic strain tensor,which can be treated as one typical source of the eigenstrain.

The hierarchical multiscale model assumes that material behavior is periodic at micro-scale,and one can propose a nondimensional parameter 0＜ζ≪1 to describe the ratio between characteristic lengths of the micro-and macro-scale.Two coordinate systems,xiandyi,are defined in macro-and micro-scale,respectively,and the relationship between two coordinates are given as

where the first and second term of the right-hand-side term in Eq.(5) denote a slow variation in the macro-scopic,and rapid variation in the micro-scopic,respectively.In this way,the strains at different orders can be derived by substituting Eq.(5) into geometry equation in Eq.(1).Next,the stresses at different orders can be defined by the constitutive models.In this manuscript,the first two leading terms in Eq.(4) are considered,which is referred as first-order mathematical homogenization theory.The merit of this approach is that the contribution ofζwill be canceled out in the derivation of micro-scopic kinematics and kinetics.However,in the high-order theory,as more terms in the asymptotic expansion are considered,the physical size of unit cell should be introduced to evaluate high-order kinematics,for example,gradient of strain[12,13].

Based on the asymptotic expansion of field quantities,one can divide the mechanical problem in the composite domain into a two-scale problem,say,the fine-(micro) and coarse-scale (macro)problem,denoting by superscriptfandc,respectively.For details of hierarchical multiscale models,please read textbook [11].

The first-order computational homogenization (FOCH) method studies a unit cell problem (or fine-scale problem) with strong form:

whereΘis the unit cell domain.The geometry of the unit cell domain is assumed to be well-defined,say,the micro-scopic shape of different material phases can be precisely constructed.Accordingly,a finite element mesh can be defined with a number of nodes and elements.The strong form defined in Eq.(6) then can be equivalent to weak form,and the weak form can be solved by classic nonlinear finite element method,with predefined discretized mesh.The solution,including fine-scale displacement,strains,stresses,and/or material internal state variables,is obtained when the nonlinear system reaches equilibrium state.Coarse-scale stresses are defined by volumetric averaging of fine-scale stresses:

where |Θ| represents the volume (three-dimensional problem) or area (two-dimensional problem) of unit cell.In addition,coarsescale material tangent stiffness matrix can be derived by homogenization.

In summary,FOCH is able to evaluate fine-scale field quantities on nodes (displacement) and elemental integration points(strains,stresses,state variables).The fundamental methodology here is the classic finite element method,so that it is easy to implement with help of a finite element toolkit.One can refine mesh where stress localization occurs so that fine-scale nonlinear evolution can be precisely captured,which helps for better understanding the nonlinear mechanism of material evolution through fine-scale to the coarse-scale.However,it is worth mentioning that the complete nonlinear finite element procedure should be repeated at every coarse-scale material integration point,and every coarse-scale Newton-Raphson iteration.The total computational cost could reach a huge amount,and usually,the FOCH method cannot be utilized for a large macro-scopic structure.

A simple flow-chart of FOCH method at one coarse-scale integration point is depicted in Fig.1.At coarse-scale,temporal domain is decomposed into a number of consecutive increments,while a number of iterations may be taken within one increment in order to reach the residual-free status.At every macro-scopic iteration,coarse-scale strains are first updated at all elemental integration points,and next coarse-scale stresses as well as consistent tangent stiffness matrix are to be evaluated.Figure 1 demonstrates the procedures of stress-updating via FOCH method.

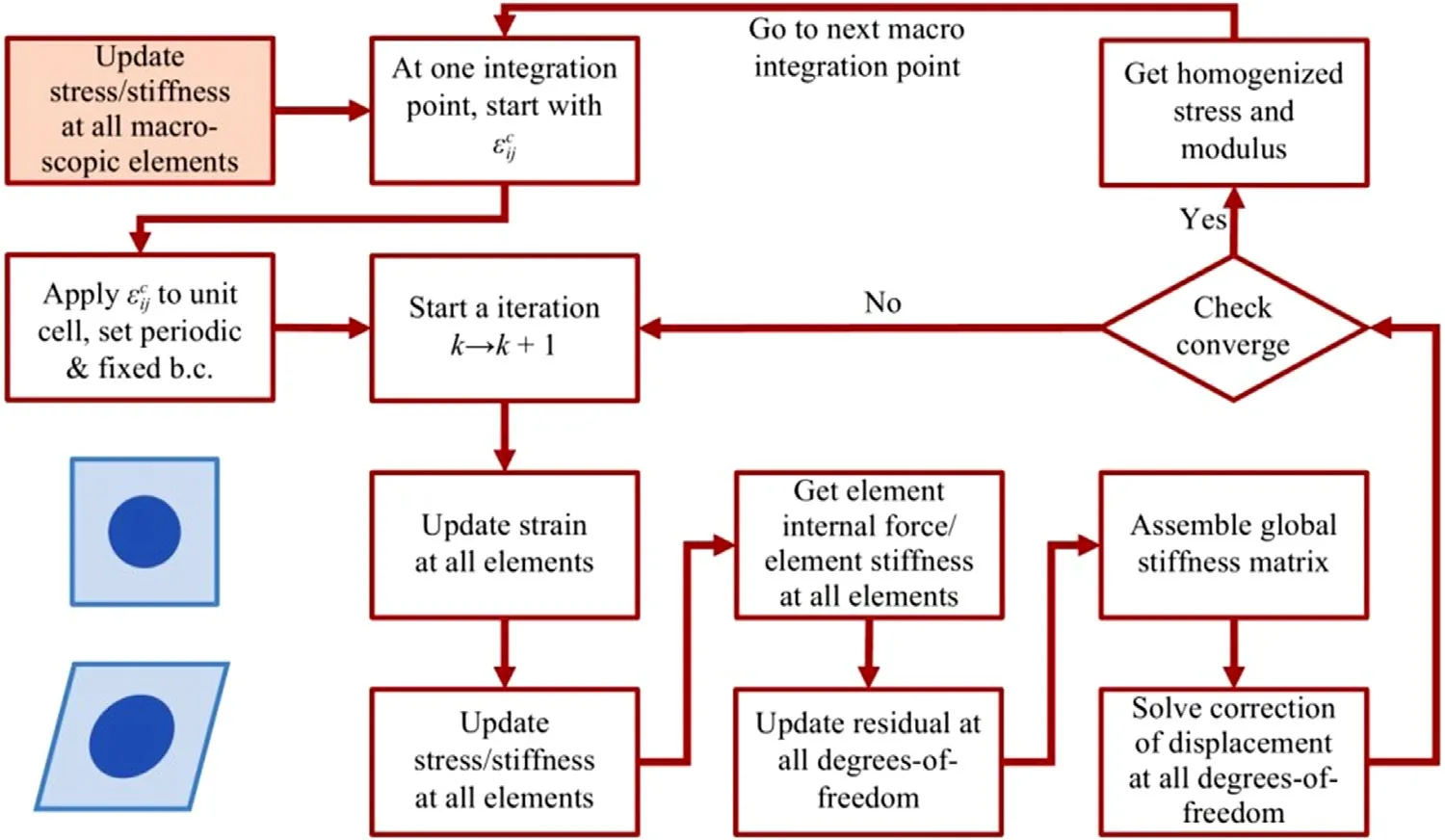
Fig.1. A flow chart for the FOCH problem at one macro-scopic integration point.

ROH method origins from Refs.[14-16],(also see textbook [11]).In the ROH method,the micro-scale geometry is still assumed to be well-defined.However,the geometric structure is not discretized into finite elements,but replaced by so-called partitions.Each partition occupies a spatial domain with same material type.All field quantities are assumed to be constant over one partition.Thus,there are no nodal field variables (like displacement)to be solved in the fine-scale.The unknowns of the system are the strains at all partitions,governed by the nonlinear equations:

whereMijklis the fourth-order compliance matrix.Thus,the nonlinear system Eq.(8) calls constitutive model of each material phase.The solution of nonlinear system needs a NEWTON iterative process,as depicted in Fig.2.

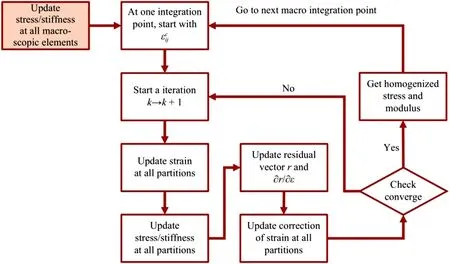
Fig.2. A flow chart for the ROH problem at one macro-scopic integration point.

One can quickly find that the size of nonlinear equation system in ROH is orders of magnitude lower than the size in FOCH.In the ROH method,strain,stress,and state variables are assumed piecewise constant over each micro-scopic partition.Thus,from the computational point view,no degrees-of-freedom are enrolled in material status update,but instead,the unknowns are replaced by strains at each partition.That is to say,a fiber-reinforced-matrixcomposite,if both fiber and matrix phases are divided into one partition for each,there are only 12 unknowns for this composite material point,i.e.,6 strain components for 1 partition.

One has proved the equivalency of strain energy density between coarse-scale and fine-scale,namely,the Hill-Mandel condi-tion:

where periodic boundary condition helps.

During the irreversible nonlinear process,energy dissipation occurs.However,due to the complexity of various material types,a strict mathematical prove is difficult to propose for general nonlinear material behaviors.Here a fiber-reinforced-matrix composite is taken as example to validate the equivalency of energy dissipation,where the matrix phase is dominated by classicJ2 rateindependent plastic model [17],and fiber phase remains elastic.The mesh and partitions are both depicted in Fig.3.

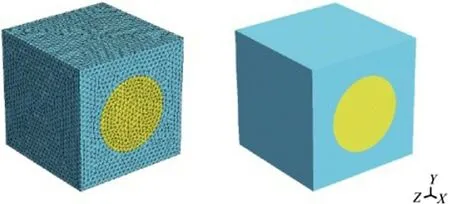
Fig.3. Unit cell mesh for the FOCH method and partitions for the ROH method.

For the classicJ2 rate-independent plastic model,the Helmholtz free energy is defined as

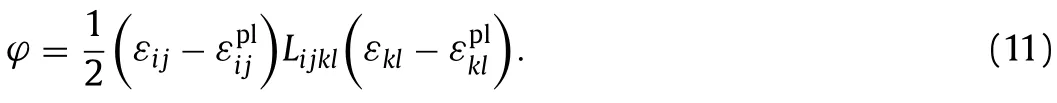
In the isothermal process,Clausius-Planck inequality is stated that the rate of dissipation energy density is non-negative,say:

Accordingly,the plastic energy dissipation density is given as

In the computational process,the time domain is discretized into consecutive increments.At incrementn→n+1,the total amount of energy dissipation at one material integration point at timet=tn+1 is evaluated as

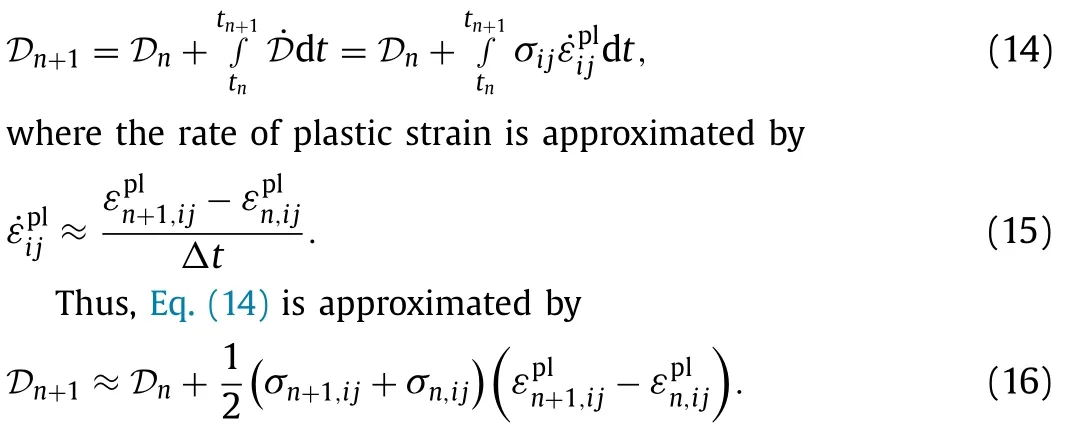
Fig.4. Fine-scale strains at peak load (left) and end of loading (right).

A simple numerical verification example can be tested first,which is a loading-unloading with uniform strain field at the coarse-scale.In the fine-scale,one can see residual strains and stresses at the end of unloading step,as depicted in Figs.4 and 5,respectively.Here the residual strains and stresses are introduced by irreversible plastic deformation at matrix phase,and the residual stresses are redistributed at micro scale.

In the first numerical example,a quarter of plate-of-hole under uniaxial tension is studied with both FOCH and ROH method,as depicted in Fig.6.The quarter of the plate is meshed into only 49 hexahedron element with full integration scheme (8 integration points per element).The number of tetrahedron elements of the unit cell shown in Fig.3 is 61,436.Roughly speaking,the total size of elements can be estimated by 61,436×49×8=24,082,912.On the contrast,the size of elements for ROH method remains the same number as macro-scopic mesh.

Fig.5. Fine-scale stresses at peak load (left) and end of loading (right).

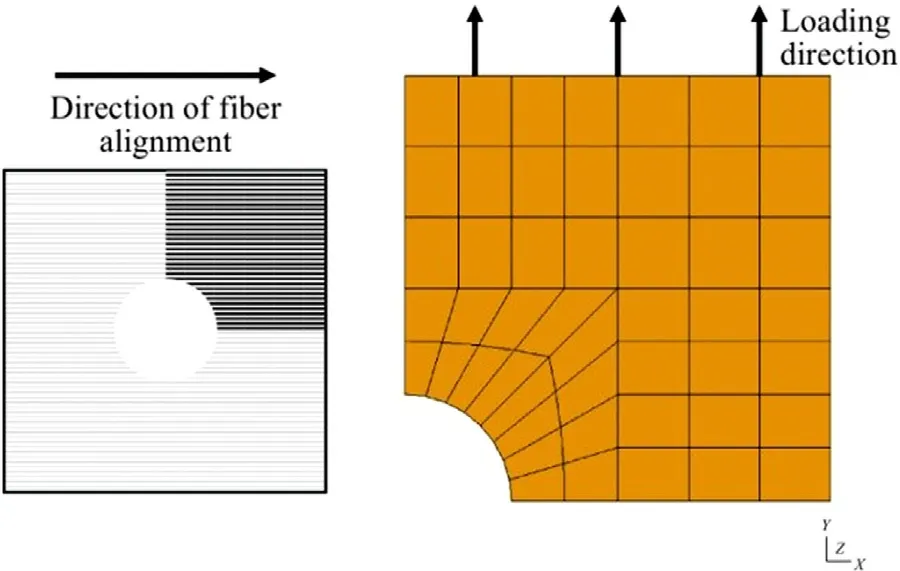
Fig.6. Geometric setup of plate-with-hole problem.

A quick comparison of macro-scopic stress distribution is given in Fig.7.Quantitatively,the total amount of elastic strain energy and plastic energy dissipation are plotted and compared in Fig.8.Here,the elastic strain energy includes the strain energy of fiber and matrix.

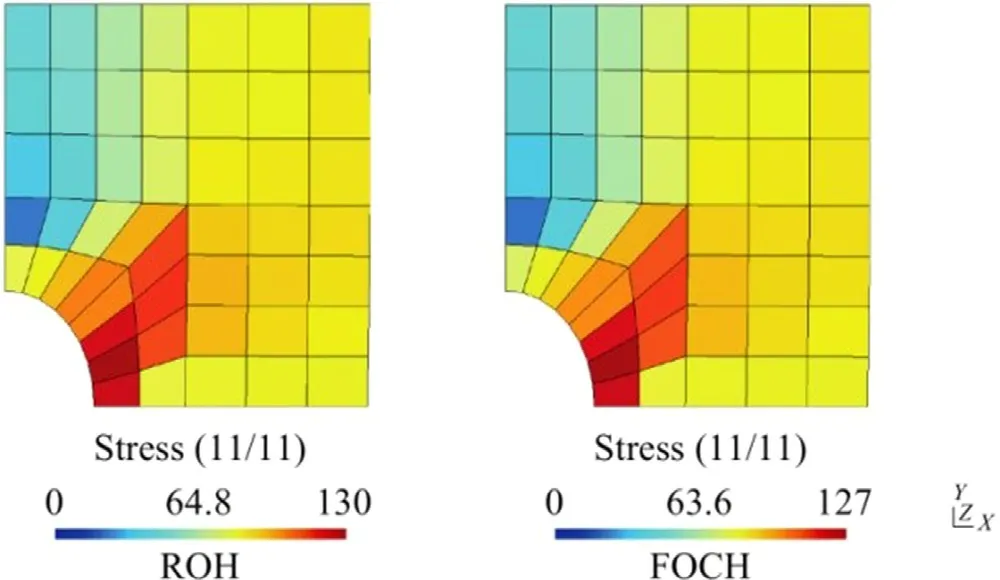
Fig.7. Comparison of macro-scopic stress in [MPa] distribution for ROH (left) and FOCH (right) methods.

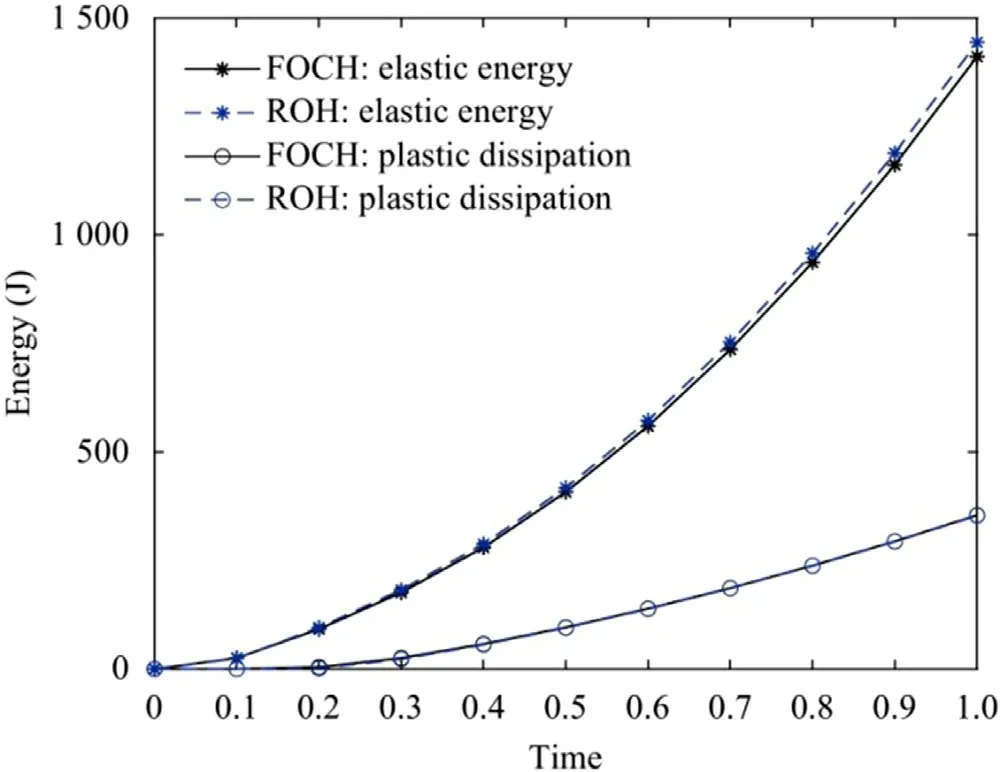
Fig.8. Comparison of total strain energy and plastic energy dissipation for FOCH and ROH methods.

Actually,the CPU time cost for FOCH is about 1.18×105s,while for ROH is about 2.39 s.If the number of macro-scopic elements increases,the CPU time of multiscale simulation through FOCH framework will be prohibitive.

Next,a 10-layup composite plate with ROH method only is simulated.Here the 10-layup structure in simulation represents the top 10 plies of a 20-layup full structure,where symmetry boundary condition is applied in the bottom surface.The orientation of the fibers is listed in Table 1.

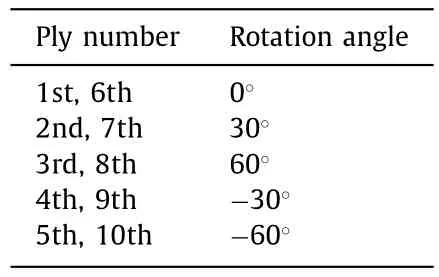
Table 1 Rotation angles of each ply.

In total,the plate is meshed into 6,800 hexahedron elements,as plotted in Fig.9.The ROH method spends about 3.45×102s for a 20-increments simulation.By the same CPU time ratio,the FOCH method will approximately cost about 197 days to finalize the simulation.

Fig.9. Finite element mesh of a 10-layup composite plate.

Here distributions of stress in [MPa] and equivalent plastic strains are visualized in Fig.10.The level of VON-MISES stress highly depends on the fiber orientation,since the stiffness of fiber is usually orders of magnitude higher than the matrix.Further-more,the field quantities at the fine-scale,like equivalent plastic strain at matrix phase,can be visualized at the macro-scopic.However,in FOCH method,the micro-scopic information can only be plotted in the unit cell.

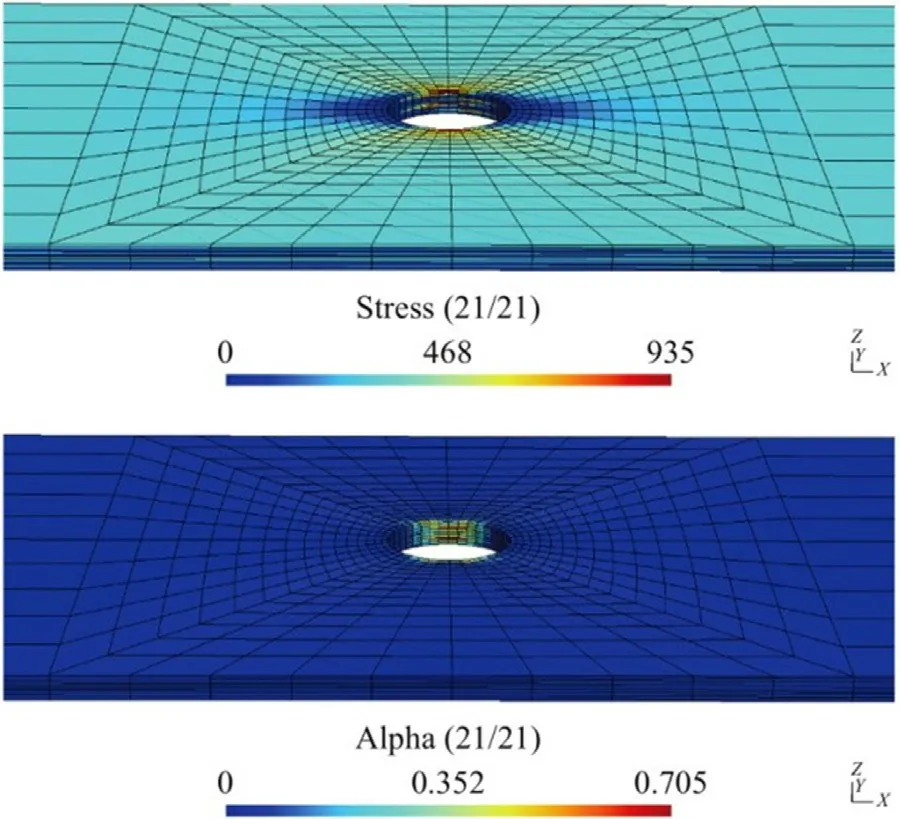
Fig.10. Stress and equivalent plastic strain distribution of the 10-layup composite plate.

In this manuscript,two hierarchical multiscale methods,FOCH and ROH,are briefly reviewed.From the point view of energy and work,the equivalency of elastic energy and energy dissipation is numerically verified for both FOCH and ROH methods.It shows that the ROH method is able to not only reproduce the same deflection-force curve but also predict the same overall amount energy quantities.The ROH method can be used practically for a general large scale macro-scopic problem.

DeclarationofCompetingInterest

The authors declare that they have no known competing _nancial interests or personal relationships that could have appeared to inuence the work reported in this paper.

Acknowledgment

Financial support by the National Natural Science Foundation of China (Grant No.11988102) is gratefully acknowledged.