Stable heat jet approach for temperature control of Fermi-Pasta-Ulam beta chain
2021-07-29BiyiliLiuQinZhngShoqingTng
Biyili Liu ,Qin Zhng ,Shoqing Tng,*
a School of Physics and Electronic Engineering, Center for Computational Sciences, Sichuan Normal University, Chengdu 610066, China
b HEDPS and LTCS, College of Engineering, Peking University, Beijing 100871, China
Keywords: Atomic simulation Finite temperature Machine learning Heat jet approach
ABSTRACT In this paper,we propose a stable heat jet approach for accurate temperature control of the nonlinear Fermi-Pasta-Ulam beta (FPU-β) chain.First,we design a stable nonlinear boundary condition,with co-efficients determined by a machine learning technique.Its stability can be proved rigorously.Based on this stable boundary condition,we derive a two-way boundary condition complying with phonon heat source,and construct stable heat jet approach.Numerical tests illustrate the stability of the boundary condition and the effectiveness in eliminating boundary reflections.Furthermore,we extend the bound-ary condition formulation with more atoms,and train the coefficients to eliminate extreme short waves by machine learning technique.Under this extended boundary condition,the heat jet approach is effec-tive for high temperature,and may be adopted for multiscale computation of atomic motion at finite temperature.
Atomic simulations at finite temperature have become instru-mental for studying thermodynamic properties [1-4] and struc-tural defects of nano-scale materials [5-7] .In an efficient and accu-rate finite temperature simulation,it is crucial to choose an appro-priate heat bath,which heats the lattice system accurately to the target temperature and preserves internal macro-motion without nonphysical deformation.Nonlinearity and macroscopic deforma-tion further challenge simulations,especially at high temperature.More precisely,due to nonlinearity,phononical modes couple with each other and induce high-frequency short waves.This makes most existing boundary conditions fail.The numerical boundary reflections then cause temperature drift and numerical instability.Thus it is difficult yet important to design an efficient artificial boundary condition,realizing simultaneously temperature control and boundary reflection suppression.
Eliminating boundary reflections for short waves in nonlinear lattices is a tough issue.For linear lattices,many efficient non-reflecting boundary conditions are available,such as variational boundary condition [ 8,9 ],time history kernel boundary condition [10-12],and matching boundary condition [13-15],etc.However,they are all derived in the linear wave framework.Their applica-bility to nonlinear lattices has not been well explored,despite that numerical tests were performed.
On the other hand,the non-reflecting boundary conditions and heat bath do not comply with each other in general.Classical heat bath methods,such as Anderson heat bath [16],Berendsen heat bath [17],Nose-Hoover heat bath [ 18,19 ],and Langevin heat bath [20] efficiently control the temperature by adjusting the momen-tum of each atom.These methods usually adopt a fixed or free boundary condition.They fail to simulate non-equilibrium prob-lems with non-thermal motion such as moving dislocation or crack propagation due to boundary reflections at the interface [21] .Be-sides,the phonon heat bath method efficiently control tempera-ture and suppress boundary reflections for harmonic lattices,by loading phonon heat source through time history kernel boundary condition [22] .If nonlinear effect is considered,the time history kernel boundary condition does not treat effectively short wave re-flections [12],and lead to higher system temperature.
In previous study,we developed an efficient thermostat tech-nique for atomic simulations called as the heat jet approach,com-plying the heat bath and non-reflection boundary condition with each other.The core of heat jet approach is to design a lin-ear boundary condition for injection of phonon heat source and boundary reflection suppression.We verified that the approach ac-curately controls the temperature for one-dimensional harmonic chain [23] and two-dimensional harmonic lattices [ 24,25 ].It suc-cessfully simulated a Frenkel-Kontorova chain with moving dislocation [21] at finite temperature.However,for a nonlinear chain with strong nonlinearity,such as Fermi-Pasta-Ulam beta (FPU-β)lattice,the linear boundary condition is no longer effective for suppressing boundary reflections of extreme short waves.
In this work,we design a stable nonlinear boundary condition and use machine learning technique to determine its coeffi-cients.Numerical simulations are performed,testing stability of the nonlinear boundary condition and the effectiveness in eliminating boundary reflections.We extend the stable nonlinear boundary condition with more atoms,and train it to eliminate extremely short waves by machine learning technique.With the extended boundary condition,we propose the heat jet approach as a thermostat for the FPU-βchain at high temperature.
Consider a monoatomic chain with pairwise FPU-βpotential [26],each atom interacts with two adjacent atoms only.The Hamiltonian of the FPU-βchain reads

wheremis the mass,unis the displacement ofnth atom away from its equilibrium position,κis the elastic constant,andβis the strength of nonlinearity.To be specific,we choose aluminum massm=4.48 ×10-26kg and lattice constanta=4.049 °A as the characteristic mass and length.Considering atomic thermal vibration typically at picosecond [27],we choose the characteristic timetc=1 ×10-12s.

Following the idea in Refs.[14,28],we aim at designing a stable boundary condition for the FPU-βchain.To this end,we define a Hamiltonian of the finite FPU-βchain withNatoms

The first term is the kinetic energy,and the second term is the FPU-βpotential energy.The last two terms represent the potential energy of atoms adjacent to the boundary.
After some calculations,the time derivative is

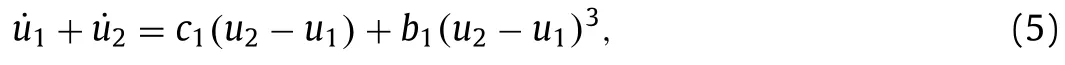
with coefficientsc1≥0 andb1 ≥0.The right boundary is treated similarly.This guarantees

Next,we determinec1andb1by machine learning technique.The numerical algorithm is described as follows.
The king looked on for a little, and then returned with his attendants to the palace, reflecting all the while on the extreme lightness of his proposed bride and the absurdity10 of having a wife that rose in the air better than any kite
Consider the domainΩ={1,2,···,N} without thermostat,andNis big enough.Choose an interior atoml∈Ωas the virtual boundary.We take a Gaussian hump as initial condition

This can be solved by sequential quadratic programming (SQP)method.
WithN=1600,l=673,τ=0.001 andk=(0,1,···,7)×105,the coefficients are found to bec1=1.9982 andb1=1.0001 ×10-12.
To simulate the FPU-βchain at finite temperature,we adopt the heat jet approach for thermostatting [23].The core idea is to design a two-way boundary condition based on the non-reflecting boundary condition to load external heat flux into the atomic region.Assuming that a right-going wave is input in the form ofwj(t)(j=1,2,3)for thejth atom,we replaceujbyuj-wjin Eq.(5) and obtain the two way boundary condition

Heat sources are injected by the two-way boundary conditions,without modifying the governing equations for the interior domain.The left heat sources are superposed by right incoming waves
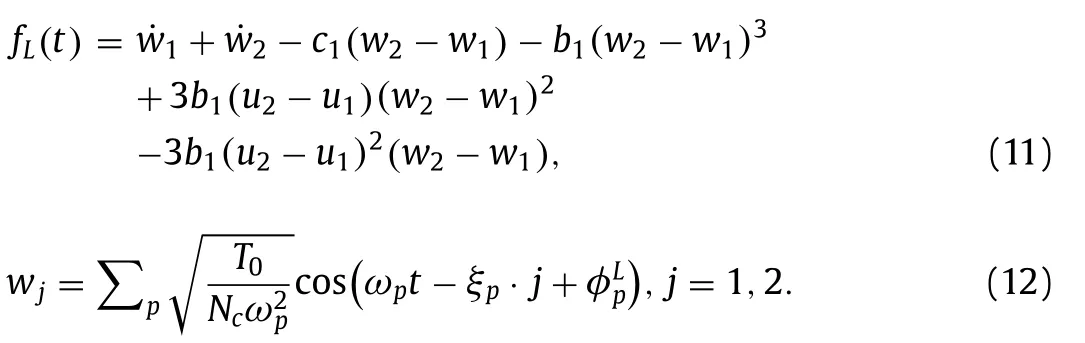
Here,ξp=2πp/Nis the wave number,ωp=2sin(ξp/2)is the normal mode frequency,pis an integer,andNcis the total number of the normal modes.The phaseφLpis randomly chosen in the interval [0,2π].The wave numberξpof the phonon representations is within [0,π].In numerical simulation,we take the wave number band to [π/8,7π/8],which is broad enough for describing the thermal field.The right boundary and heat source are treated in the same manner.
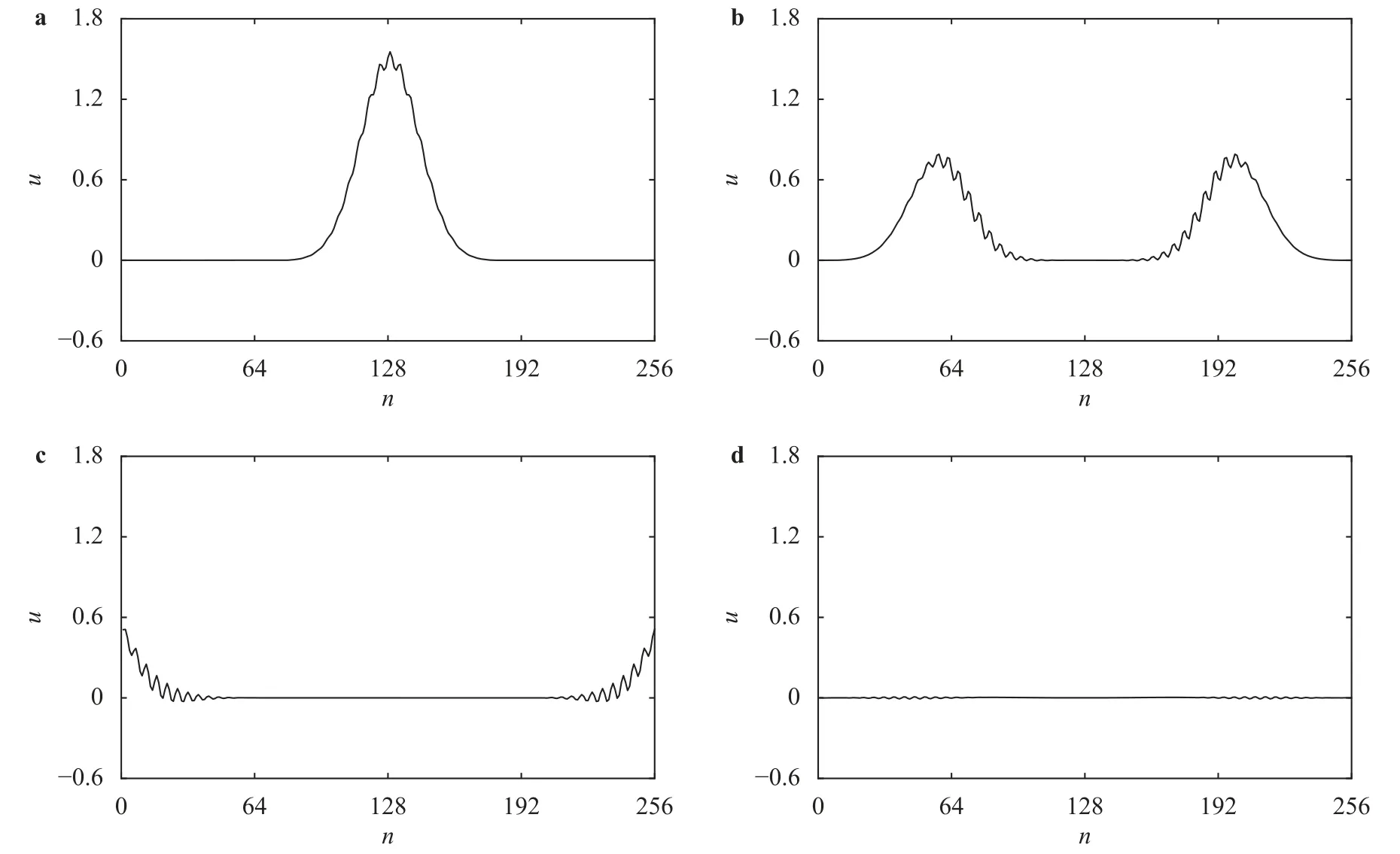
Fig.1. Propagation of the Gaussian hump in the FPU-β chain at zero temperature: a u n(0), b u n(70), c u n(140),and d u n(210).
For low temperature,the normal modes are independent of each other.Supposing that the incident waves are completely injected into the lattice system and boundary reflections are neglected,the lattice solution can be approximately written as
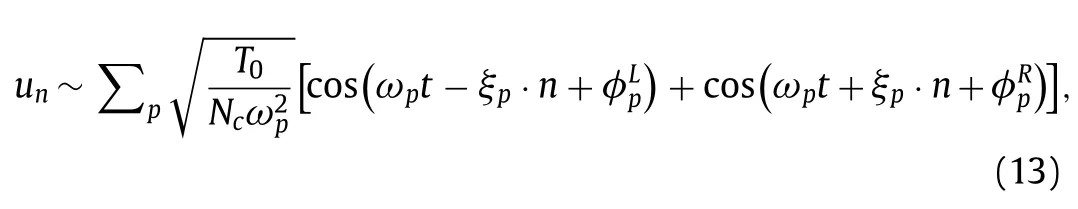
which is the superposition of incident waves from two sides.With the approximate lattice solution,we can obtain the time average of the Hamiltonian for a single atom
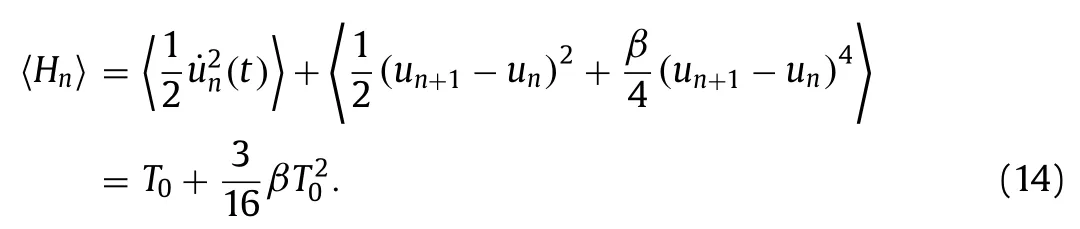
Here,〈·〉 represents long time average.From the above formula,we observe that the energy of each atom is higher thanT0,which is caused by the fourth power term in the FPU-βpotential.Thus the final system temperature is expected to be higher than the heat source temperature.
For the chain at a low temperature or with a small nonlinearity coefficientβ,the second term in Eq.(14) is much smaller than the first one,therefore the temperature deviation caused by nonlinearity can be neglected.However,for the chain at a high temperature or with a big nonlinearity coefficient,the nonlinearity potential will make the system temperature considerably higher thanT0.Besides,the phononical normal modes couple with each other,and generate many short waves.These short waves move slowly and cause boundary reflections,which also contribute to deviation of the system temperature.
In all computations,we use the velocity verlet scheme with a time step dt=0.01 for time integration of Newton’s equation.The velocity verlet scheme is an energy-conserved symplectic algorithm [30,31],which is indispensable for long-time atomic simulations.We remark that the second order Runge-Kutta method may exhibit instability for long time simulations [32].Unless otherwise specified,we take the FPU-βchain withN=256 atoms and the nonlinear coefficientβ=0.1.
First,we test the effectiveness and stability of the nonlinear boundary condition,which are supplied to the two ends of the FPU-βchain.The initial displacement profile is set as a Gaussian hump different from Eq.(7)
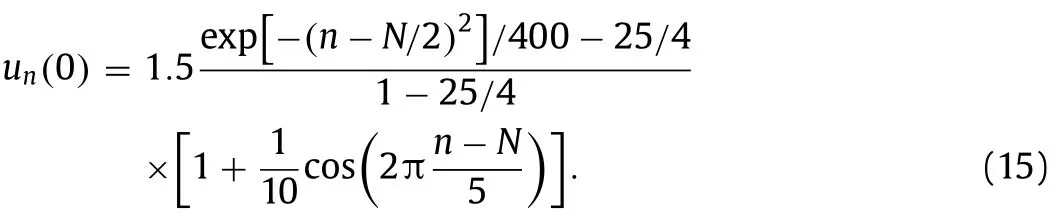
As shown in Fig.1,the initial Gaussian hump is superposed with some short waves.It splits into two humps propagating toward both sides.At timet=140,the wave fronts reach the boundaries,and vanish without obvious reflections.After a short time,the long waves and most short waves have completely gone out of the system,leaving few high frequency waves reflected by the boundaries.This test demonstrates that the nonlinear boundary condition is effective to eliminate boundary reflections for outgoing waves with a broad band of wave number.At the same time,we display the total Hamiltonian in Fig.2.It strictly decays along with time.The first platform corresponds to the stage when the Gaussian hump moves within the chain.The later platforms represent the reflected short waves propagating in the chain,which are gradually diminished by the boundary condition.The total Hamiltonian of the FPU-βchain becomes very small aftert=800.This test illustrates the stability of the nonlinear boundary condition.
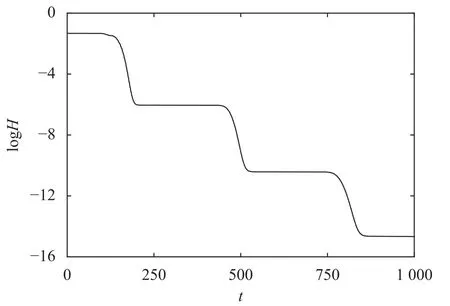
Fig.2. Hamiltonian of the FPU-β chain for the Gaussian hump.Logarithm base is e.
Then we perform a test for the heating process.The twoway boundary condition Eq.(10) with the phonon heat source Eqs.(11) and (12) is applied to the two ends of the FPU-βchain.Setting all atoms at equilibrium,we inject heat source at temperatureT0=0.5639 (300 K).As depicted in Fig.3a,the system temperaturefluctuates around a mean value.In Fig.3b,the average kenitic energy (local temperature)Tn=(t)dtdistributes uniformly in space with the cut-off timetc=2 ×104and the total computing timet=1 ×106.The system temperature and the local temperature is higher than the heat source temperatureT0.The temperature drift mainly comes from the boundary reflections of short waves.As nonlinear effect exists in the FPU-βchain,thermal fluctuations induce short waves with wave number close to π,which causes boundary reflections and leads to higher temperature.In the following,we design multipoint (i.e.multi-atom) boundary conditions to better eliminate boundary reflections for extremely short waves.
Notice the form of Eq.(5),we propose a multi-point boundary condition
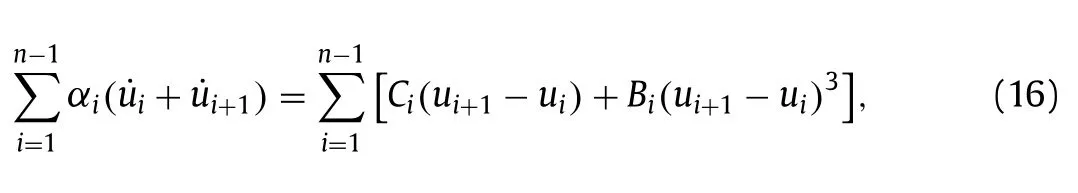
whereCi=αici,Bi=αibi,andαi>0 is the weight withα1=1.will be obtained by constrained ridge regression.Whenn=2,this boundary condition degrades to Eq.(5).But whenn >2,we do not require the Hamiltonion strictly decreasing.Taking the Gaussian hump Eq.(7) to train the four-point boundary condition (n=4),we obtain the coefficients of Eq.(16) shown in Table 1.

Table 1 Coefficients of Eq.(16) when n=4.
Same as before,we replaceuibyui-wiin Eq.(16) and obtain the two-way boundary condition

The incoming wavewi(i=1,2,3)is defined in Eq.(12).
Now,we apply the heat jet approach with the four-point boundary condition to the FPU-βchain,and perform a similar test for heating process withT0=0.5639 (300 K).As shown in Fig.4,the system temperature and the local temperature fluctuate uniformly around a mean of 0.5850,which is close toT0.Comparing with Fig.3,the heat jet approach with the four-point boundary condition better controls temperature.The boundary condition with more atoms appears more effective to capture outgoing waves with broader wave numbers based on machine learning training.The multi-point boundary condition effectively injects phonon heat sources,at the same time well eliminates reflections of long waves and extremely short waves.
High temperature leads to strong nonlinearity,making it more difficult to control the temperature and to eliminate the boundary reflections.To test whether the heat jet approach endures high temperature,we simulate the FPU-βchain at temperature,which is close to the melting point of aluminum.As shown in Fig.5,the system temperature and the local temperature fluctuate aroundT=1.7787,which is close to the heat source temperatureT0.This implies that the four-point boundary condition is applicable to even higher target temperature.
In this paper,we successfully design energy-based nonlinear boundary conditions,and apply them to the heat jet approach.This realizes temperature control for the nonlinear FPU-βchain even at high temperatureT0=1.6917 (900 K).The novel nonlinear boundary condition is proposed and combined with machine learning technique to determine its parameters.Stability has been theoretically and numerically verified.In fact,more accurate temperature control can be designed by choosing training data that better represents thermostat,and by modifying the heat source.This way of designing heat jet approach may be extended to other nonlinear lattices,and the resulting heat jet approach may be applied to multiscale computations of atomic motion at high temperature.

Fig.3. Heating process for the FPU-β chain with the nonlinear boundary condition at T0=0.5639 (300 K): a system temperature and b kinetic temperature.
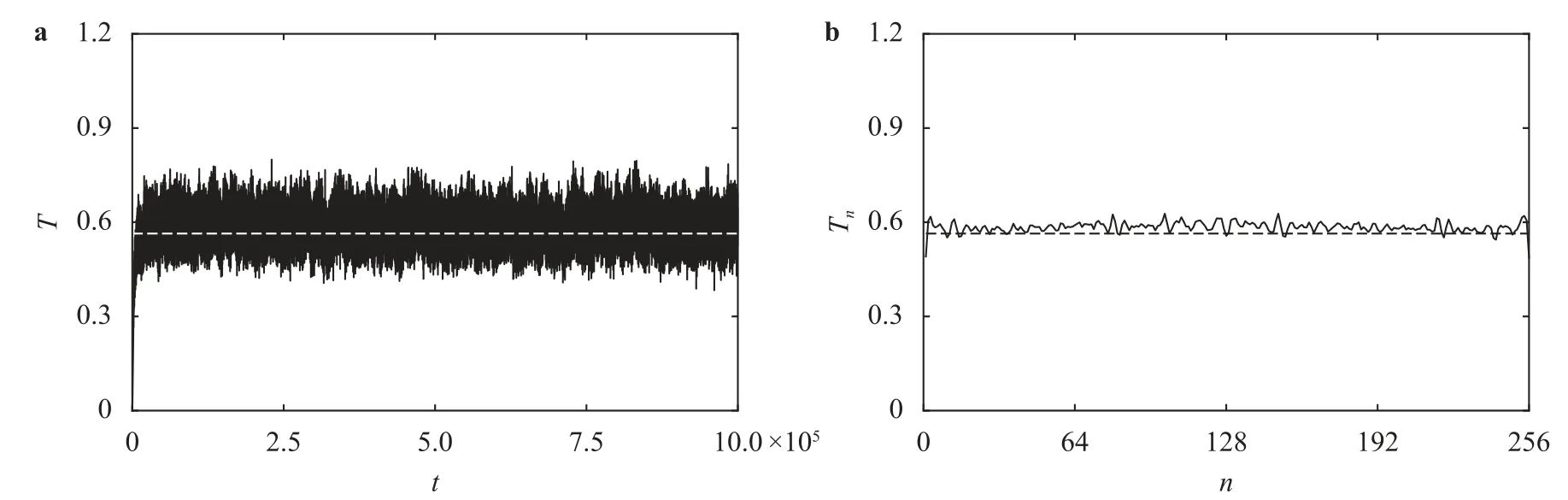
Fig.4. Heating process for the FPU-β chain with the four-point boundary condition at T0=0.5639 (300 K): a system temperature and b kinetic temperature.
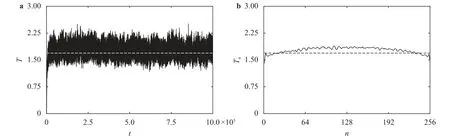
Fig.5. Heating process for the FPU-β chain with the four-point boundary condition at T0=1.6917 (900 K): a system temperature and b kinetic temperature.
DeclarationofCompetingInterest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This research was partially supported by the National Natural Science Foundation of China (Grants 11988102,11521202,11832001,and 11890681).
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Experimental investigation of sound absorption in a composite absorber
- A study of inner-outer interactions in turbulent channel flows by interactive POD
- A study on equivalence of nonlinear energy dissipation between first-order computational homogenization (FOCH) and re duce d-order homogenization (ROH) methods
- Rotational dynamics of bottom-heavy rods in turbulence from experiments and numerical simulations
- Wall-resolved large-eddy simulation of turbulent channel flows with rough walls
- Constraine d large-e ddy simulation of turbulent flow over inhomogeneous rough surfaces
