球扁钢的矫直角及轴向矫直解析模型
2021-07-29胡如夫陈春梅
殷 璟,胡如夫,陈春梅
(宁波工程学院 机械工程学院,浙江 宁波 315336)
0 引言
球扁钢是船舶专用结构型钢,是建造航母、战舰、货轮、破冰船等大型船只所必需的重要龙骨钢材[1],其特点是截面不对称使冷却过程中温度分布不均,从而造成严重的内应力弯曲,矫直前挠度通常超过30 mm/m,且在纵向和水平方向均有初始弯曲,如图1所示。国标GB/T 9945—2012规定,球扁钢的残余挠度应小于3 mm/m,总挠度不大于总长度的0.3%,因此球扁钢矫直时需在专用矫直机上,借助特殊形状的矫直辊对两个方向同时进行矫直。

图1 矫直前的球扁钢Fig. 1 Bulb-flat steel before straightening
球扁钢因轧制过程中不一致的压下率和冷却过程中不均匀的温度场致使弯曲问题严重[2-3],研究人员立足于生产实践,提出了一些解决该问题的方案。魏振洲等[4]提出采用双根对称轧制法,解决球扁钢的轧制不对称和冷却不对称问题,并给出了具体的孔型设计和轧制方案;吴维等[5]发现球扁钢在轧制过程的扭转变形与轧制压下量和轧件长度有关,提出轧件长度取轧件原始厚度的10 倍进行轧制,能够明显减少球扁钢的扭转变形;李秋红等[6]通过有限元法模拟了球扁钢的冷却过程,其截面温度场分布说明冷却不均是引起球扁钢弯曲的主要原因,提出通过对球扁钢进行轧前、轧后水冷的措施来解决该问题,并介绍了球扁钢轧后水冷装置的布置和设计;李建华等[7]提出终轧后设置喷雾嘴对内侧表面进行强制冷却以及增加冷床预弯功能,可有效提高球扁钢的成材率。
从上述研究成果中可以发现,目前针对球扁钢的大部分研究主要集中于对球扁钢初始弯曲原因的分析及如何在轧制和冷却过程中减小球扁钢的初始弯曲。但在球扁钢的生产过程中,轧制和冷却的不均匀、不对称是不可避免的,即使通过多种途径减小球扁钢的初始弯曲,仍需多辊矫直机矫直才能达到其平直度要求。在球扁钢的矫直过程中,最重要的是矫直角和轴向矫直规程的制定,但由于球扁钢的截面形状完全非对称,使其矫直工艺的理论研究较为困难[8-9],生产中工艺规程的制定主要依赖技术人员的经验,调试成本高、周期长。因此,建立一种球扁钢轴向矫直解析模型为其矫直角和轴向矫直规程的制定提供理论依据,从而提高球扁钢的矫直效率和矫直精度十分必要。
1 球扁钢的双向同矫工艺
球扁钢初始弯曲的特点是纵向为“波浪弯”,轴向为“镰刀弯”,生产中球扁钢采用双向同矫的方式,即:纵向连续往复弯曲矫直,轴向单向反弯曲矫直。因此球扁钢矫直机与普通矫直机略有不同。首先,球扁钢矫直机的矫直辊为圆锥形,使球扁钢矫直时与水平面呈一定角度,有利于减小轴向矫直力,同时可提高矫直辊的通用性,降低了换辊成本;其次,为满足球扁钢双向同矫的要求,球扁钢矫直机的下排辊轴向可调,上排辊纵向和轴向均可调。当球扁钢倾斜进入矫直机后,上排矫直辊的纵向压下使球扁钢发生连续往复弯曲变形,以矫直其z向初始挠度;将各矫直辊的轴向位置调整成一条与球扁钢轴向初始挠度方向相反的反弯曲线,使球扁钢发生单向反弯曲变形,以矫直其y向初始挠度。球扁钢的双向同矫工艺如图2所示。
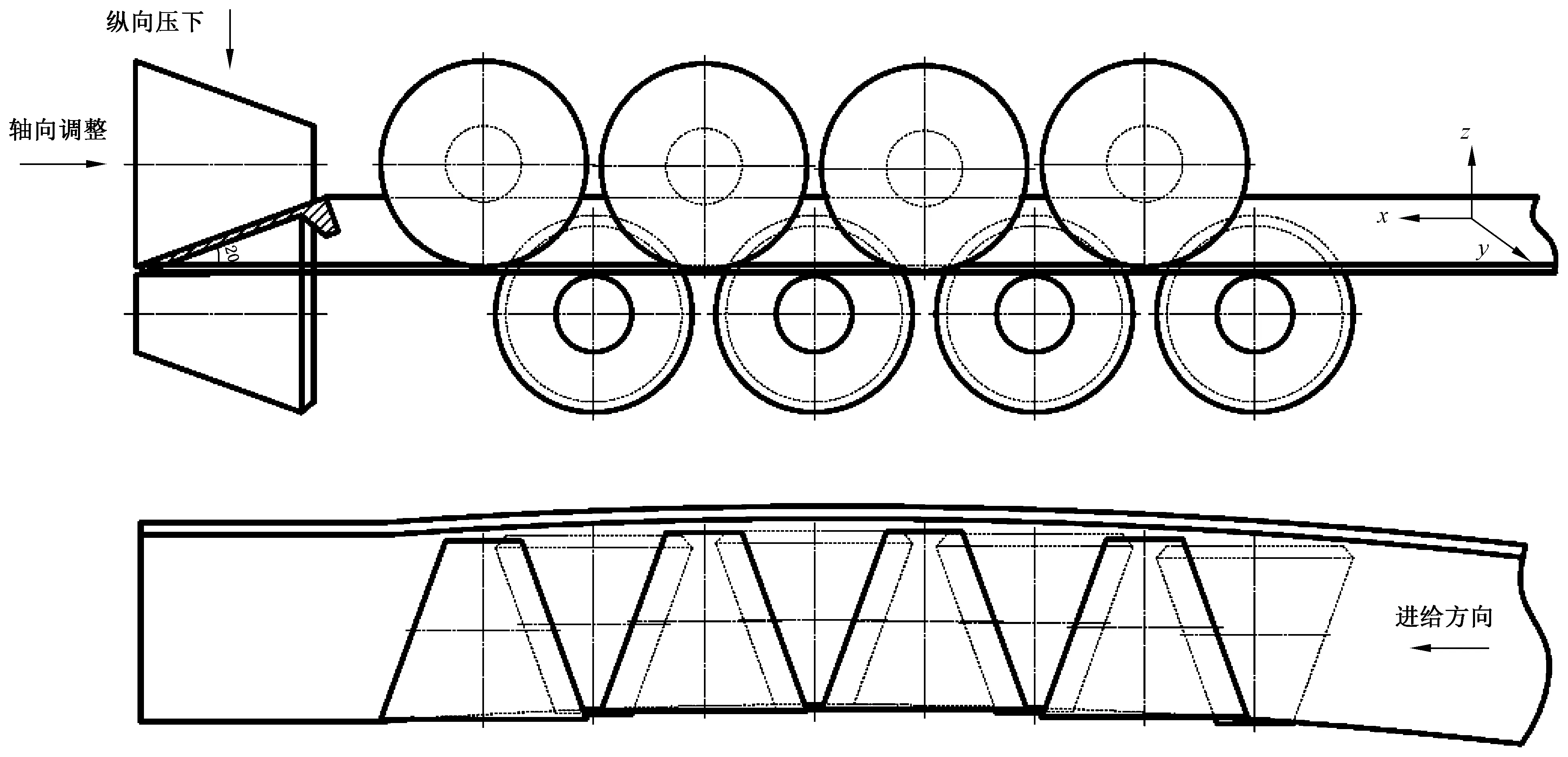
图2 球扁钢双向同矫工艺示意图Fig. 2 Diagram of double-direction straightening for bulb-flat steel
在实际生产中发现,球扁钢的纵向初始弯曲率并不大,部分规格的球扁钢在轧制冷却后,其z向初始挠度甚至是满足国标中对平直度要求的,因此球扁钢的矫直重点是轴向(即y向)大初始曲率弯曲,其关键参数是矫直角和轴向矫直规程。
2 球扁钢截面简化及参数化
球扁钢截面如图3所示,其截面参数分别为:高度h,宽度b,腹板厚度t1,球顶面与腹板间的圆角半径、球端圆角半径r1,腹板端部圆角半径r,重心距离dx。
为便于分析计算,球扁钢截面按以下方式简化:球扁钢腹板端部圆角半径r很小,忽略不计后简化为直角;球端圆弧部分简化为与原弧面相切的直线,宽度为t2;球顶面与腹板间的球端圆弧,简化为直线相交。简化后的球扁钢截面如图3中虚线所示。通过数学方法可证明,球顶宽度t2与球头圆角半径r1有如下关系:
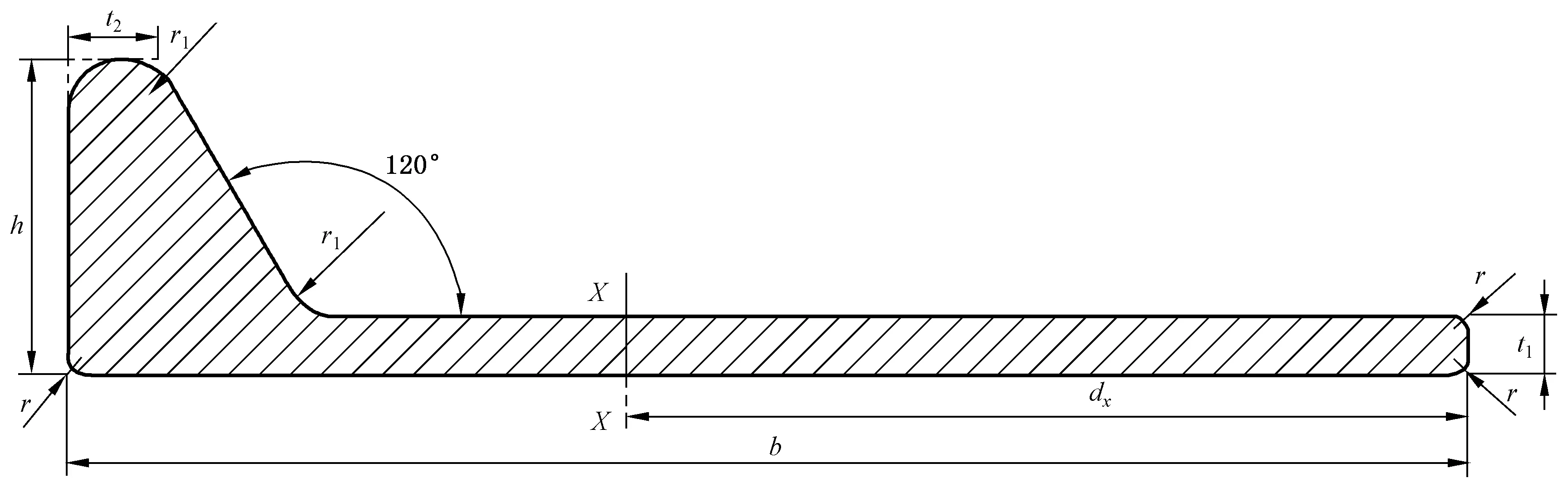
图3 球扁钢截面参数Fig. 3 Sectional parameters of bulb-flat steel
为检验截面简化对截面属性的影响程度,以截面面积A和重心距离dx作为截面简化前后的对比参数,对比范围是国标GB/T 9945—2012列出的全部54个规格的球扁钢,对比结果如图4所示。

图4 球扁钢截面简化前后参数对比Fig. 4 Comparison of parameters before and after section simplification for bulb-flat steel
数据显示,简化后面积相对偏差的最大值为1.304%,平均值为0.656%;重心距离相对偏差的最大值为0.621%,平均值为0.404%。因此,简化后的球扁钢截面特征和参数可以较为准确地反映原截面的几何特征,由截面简化引入的计算误差较小。

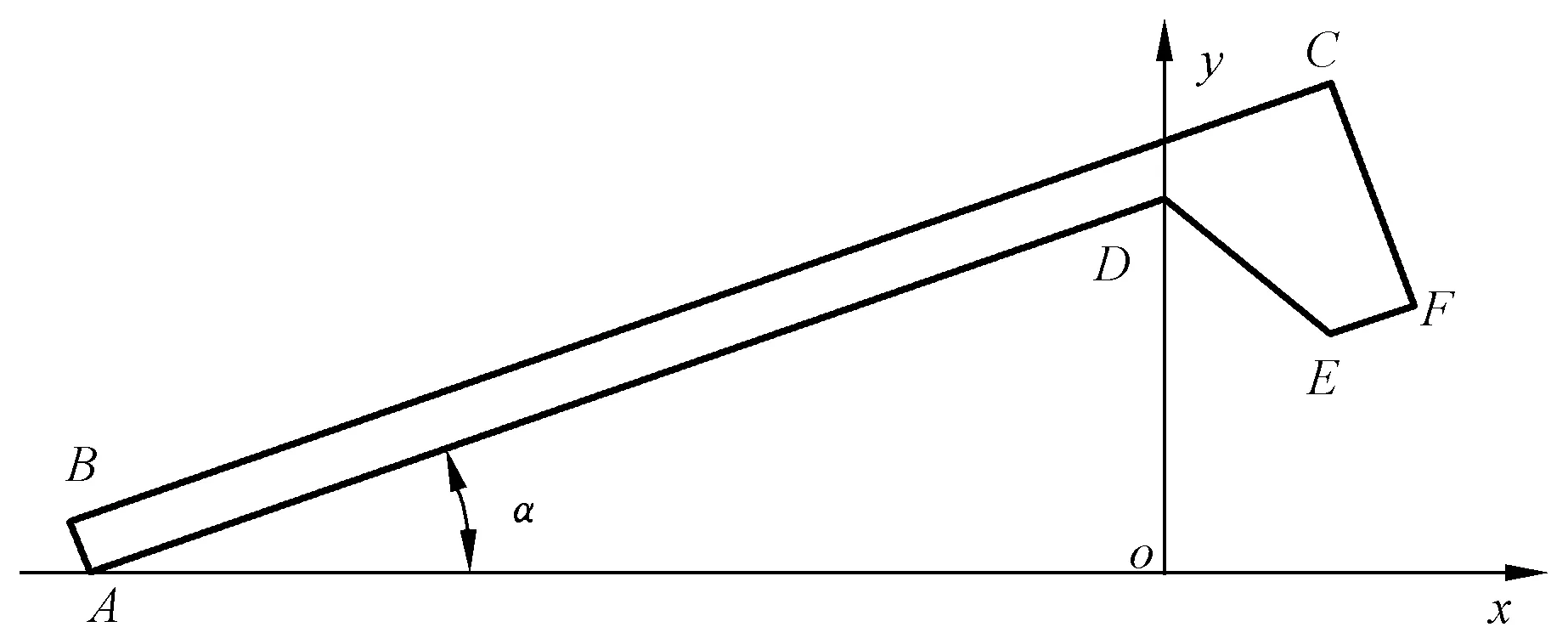
图5 球扁钢截面参数化Fig. 5 Section parameterization of bulb-flat steel
(1)
(2)
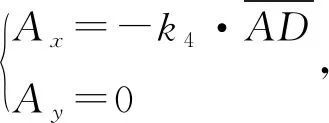
lAB:y=k3(x-Ax),
lBC:y=k1(x-Bx)+By,
lCF:y=k3(x-Cx)+Cy,
lDE:y=k2·x+Dy,
lEF:y=k1(x-Ex)+Ey。
3 球扁钢的矫直角
出于矫直工艺的考虑,球扁钢矫直时,腹板与水平方向呈一定夹角,即矫直角。如图6所示,当球扁钢自然朝下放置时,腹板与水平方向的夹角是最小矫直角,用αmin表示。根据几何关系,有
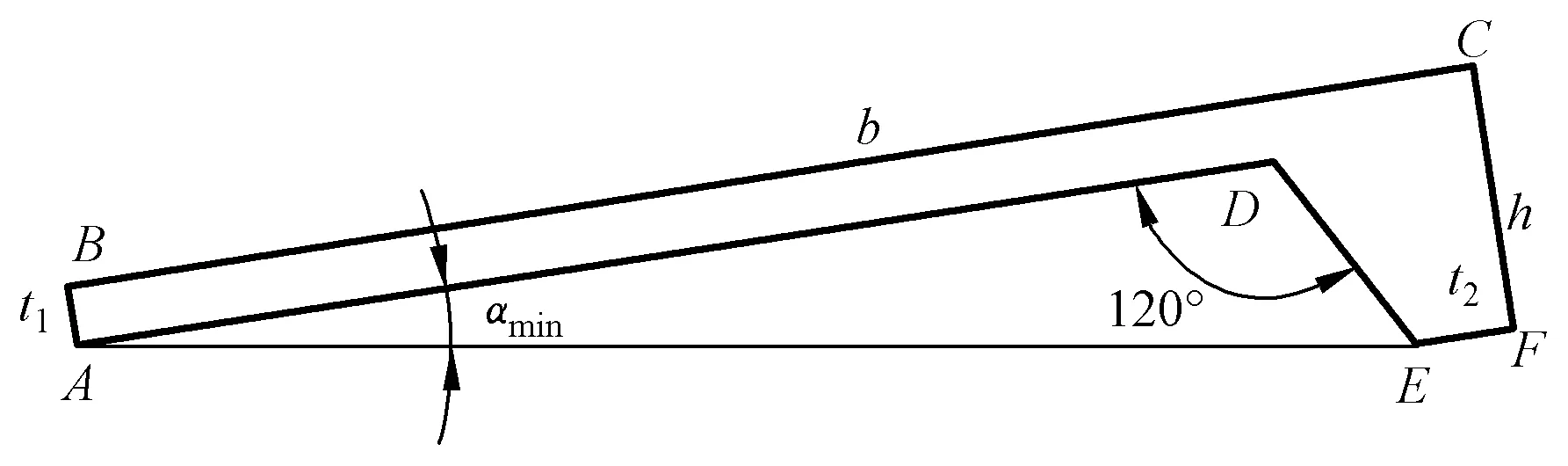
图6 球扁钢最小矫直角Fig. 6 The minimum straightening angle of bulb-flat steel
(3)
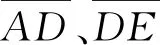
αmin=arccos(cosαmin)。 (4)
由式(4)计算出全部国标规格球扁钢最小矫直角αmin的范围是8.23°~10.75°。而球扁钢矫直角的确定还要综合考虑其对矫直力和矫直质量的影响。通过计算发现,当矫直角为20°时,球扁钢截面对纵向形心线的惯性矩比腹板平放时小6%左右,这就意味着矫直角使轴向矫直力减小,且矫直角越大,轴向力就越小。通常,球扁钢矫直机设计的最大轴向载荷是纵向最大载荷的60%左右,因此减小轴向矫直力对矫直机有利。从矫直质量方面考虑,当有一定矫直角时,纵向的多辊矫直过程会对侧弯有辅助矫直的作用,矫直角越大,侧弯的纵向分量越大,矫直效果越好。但矫直角不能过大,因为矫直角增大虽然会减小轴向矫直力,但会相应增加纵向矫直力,且纵向矫直力增加的绝对值大于轴向矫直力减小的绝对值。另外,过大的矫直角会使球扁钢进入矫直机时咬入困难,从而降低矫直速度,增加“摆尾”隐患。综合考虑,矫直角在15°~25°较为合适。南钢集团无锡金鑫轧钢有限公司在生产中大型规格球扁钢时均采用20°的矫直角。
值得注意的是,球扁钢轧制时为保证其断面形状的正确和提高轧辊重车次数,采用孔型的斜配角度。对于球头部开口的孔型,斜配角取10°~15°;对于蝶式孔型,斜配角取15°~16°[10]。球扁钢的矫直角与轧制时的斜配角接近或是出于相似的考虑,既能使矫直辊受力均衡,也能增加矫直辊的重车次数。
4 球扁钢轴向矫直解析模型
4.1 球扁钢轴向纯弯曲回弹分析
球扁钢的轴向矫直可视为完全非对称截面曲梁的单向反弯曲。完全非对称截面曲梁弯曲时应变中性层和几何中心层不重合,按经典弯曲弹复理论很难建立准确的弹复方程,矫直角的加入使弯曲回弹后曲率的计算更为困难。而小曲率平面弯曲弹复理论[11]的建立为该类工程问题的理论分析提供了可靠的分析方法和统一的弹复方程,并已在单向非对称截面曲梁的弯曲回弹分析中得到了应用与验证[12]。本文也将继续采用小曲率平面弯曲弹复理论分析球扁钢矫直时的弯曲回弹。
设球扁钢轴向的初始曲率半径是ρ0x,轴向反弯曲率半径是ρx,在xoy坐标系下,球扁钢几何中心层横坐标为xc,当量应变中性层的横坐标为x0,真实应变中性层的横坐标为xt,轴向初始曲率为K0x,轴向弯曲曲率为Kx,轴向当量应变中性层曲率为Kεx。由小曲率平面弯曲弹复理论,轴向反弯时的真实应变εx可表示为
εx=(x-xc)(Kεx-K0x)-(Kεx/Kx-1)=
K0x(xc-x)-Kεx(x0-x),
式中,
Kx=1/ρx,
(5)
Kεx=1/[ρx-(x0-xc)],
(6)
K0x=-1/ρ0x。
当x=xt时,真实应变εx=0,即
K0x(xc-xt)-Kεx(x0-xt)=0,
则
xt=(K0x·xc-Kεx·x0)/(K0x-Kεx)。
(7)
设球扁钢的材料性能符合简单随动强化材料模型[12],ex为轴向弹性区高度,则其弹性应变εe可表示为
εe=K0x(xc-xt-ex)-Kεx(x0-xt-ex)=σs/E,
式中,σs为屈服应力,E为弹性模量,由此可推出
ex=σs/[E(Kεx-K0x)],
(8)
则纯弯曲时球扁钢的截面应力可表示为
式中,D为塑性切线模量,σ0=(1-D/E)σs。
球扁钢轴向纯弯曲时的真实应力和真实应变如图7所示。

图7 球扁钢轴向纯弯曲应变、应力示意图Fig. 7 Schematic diagram of strain and stress for bulb-flat steel axial pure bending
由图7可知,球扁钢截面的不对称造成其纯弯曲时受拉和受压的部分也不对称,但其截面轴向受力仍然满足力平衡方程,即
Fx1=-Fx2,
式中,Fx1是真实应变中性层xt右侧应力对相应面积的积分,Fx2是真实应变中性层xt左侧应力对相应面积的积分。
显然,用解析法求解真实应变中性层xt和当量应变中性层x0的位置是非常困难的,但借助力平衡方程和数值积分法可以较为准确地求解出这两个关键参数,具体求解思路如下:
1)由截面形状可以判断x0≥xc,因此给x0赋初值x0=xc。
2)初始曲率K0x、弯曲曲率Kx均为已知量,由x0的初值可求出当量应变中性层曲率Kεx的初值,继而求出xt和ex的初值。
3)由xt的位置和ex的大小确定应力弹性区和塑性区所对应的面积范围。
4)用数值积分法求解Fx1和Fx2。
5)判断ΔFx=|Fx1+Fx2|是否大于允差ζ,程序中设定ζ=100 N。
6)如ΔFx>ζ,则给x0赋新值x0=x0+0.01(0.01是迭代步长),程序回到第(2)步进行循环。
7)如ΔFx≤ζ,则认为x0的赋值使力平衡方程成立,将其代入式(7)和式(8)可求出xt和ex,图7中应力和应变的分布被确定。
8)由小曲率平面弯曲弹复理论可知,球扁钢轴向纯弯曲弹复后的曲率Kpx为
(9)

9)球扁钢轴向最大矫直力Fx可表示为
(10)
式中,n是矫直辊个数,L是辊距。将球扁钢纯弯曲时的弯矩Mx和矫直机设备参数代入式(10),即可求得球扁钢轴向最大矫直力Fx。
借助MATLAB软件对上述分析计算过程进行编程,输入球扁钢截面的基本参数h、b、t1和r1以及初始曲率、弯曲曲率,即可计算出球扁钢弯曲回弹后的曲率,计算结果如图8所示。通过大量的分析计算发现,弯曲变形越大,当量应变中性层和真实应变中性层偏离几何中心层越远。
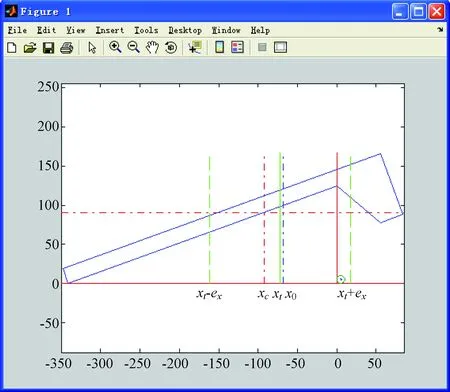
图8 球扁钢轴向弯曲程序运行结果Fig. 8 Program result of axial bending for bulb-flat steel
4.2 球扁钢轴向矫直解析模型的验证
为验证球扁钢轴向矫直解析模型的可靠性,在南钢集团无锡金鑫轧钢有限公司的8辊球扁钢矫直机上对430×20和260×10两种典型规格的球扁钢进行了轴向矫直实验。该矫直机的辊距L为1 m,矫直角为20°。球扁钢的材料性能参数如表1所示。

表1 球扁钢的材料性能Tab.1 Material properties of bulb-flat steel
430×20规格球扁钢的轧制长度为50 m,最大初始挠度达2.5 m/50 m,即初始曲率K0=7.92×10-3m-1,换算后轴向初始曲率K0x=K0cosα=7.44×10-3m-1。通过程序试算后确定,当轴向弯曲曲率Kx达到11.26×10-3m-1时,弯曲回弹后的曲率Kpx为0.271×10-3m-1,即矫后残余挠度为0.084 m/50 m,可达到国标要求。由辊距和辊数可反推出当轴向矫直规程为[0,8.5,14,17,17,14,8.5,0]mm时轴向弯曲曲率Kx为11.26×10-3m-1。将该轴向矫直规程输入球扁钢矫直机的控制系统进行矫直实验,经测量,球扁钢矫后残余挠度为0.102 m/50 m,与理论计算值较为吻合,另外实测的最大矫直力为531 kN,亦与理论计算的517 kN较为接近。
260×10规格球扁钢的轧制长度也是50 m,最大初始挠度为1 m/50 m,即初始曲率K0=3.20×10-3m-1,换算后轴向初始曲率K0x=K0cosα=3.01×10-3m-1。通过程序试算后确定,当轴向弯曲曲率Kx达到15.92×10-3m-1时,弯曲回弹后的曲率Kpx为0.025×10-3m-1,即矫后残余挠度为0.007 8 m/50 m,远小于国标要求。但在反推轴向矫直规程时发现,当轴向弯曲曲率较大时,中间几个矫直辊的轴向调整量会超过矫直机的设计标准,因此选择前6个矫直辊形成反弯曲线,后两个矫直辊的轴向调整量逐步过渡,便于球扁钢的导出,最终确定轴向矫直规程为[0,7.3,11,11,7.3,0,8.3,11]mm。将该轴向矫直规程输入球扁钢矫直机的控制系统进行矫直实验,经测量,球扁钢矫后残余挠度为0.065 m/50 m,达到了国标的矫直要求,实测最大矫直力为102 kN,比理论计算的86 kN大15.7%。
矫直实验结果说明,利用球扁钢轴向矫直解析模型可以较为准确地预测出矫直所需的轴向弯曲曲率和矫直时的最大轴向力,进而反推出轴向矫直规程,可大大缩短球扁钢矫直的调试时间。
5 结论
本文建立了精确的球扁钢几何参数化模型,基于该模型计算出全部国标规格球扁钢最小矫直角αmin的范围是8.23°~10.75°。增大矫直角可减小轴向矫直力,并能增大侧弯的纵向分量,提高矫直效果;但过大的矫直角会使纵向矫直力大幅增加,同时增加了球扁钢进入矫直机时的咬入困难,降低矫直速度,增加“摆尾”隐患。综合考虑矫直力、矫直质量和咬入条件等多种因素,球扁钢的矫直角应在15°~25°。在此基础上,本文借助小曲率平面弯曲弹复理论,建立了球扁钢轴向矫直解析模型。该模型通过引入当量应变和当量应变中性层的概念,解决了非对称截面曲梁纯弯曲时真实应变中性层和几何中心层不重合的问题,实现了球扁钢曲梁纯弯曲回弹曲率的精确计算。现场矫直实验结果表明,球扁钢轴向矫直解析模型可准确预测球扁钢轴向矫直弯曲曲率和最大矫直力,为球扁钢轴向矫直规程的制定提供了理论依据。
