基于多尺度全卷积与CRF的路面裂缝检测算法
2021-07-29张烁瑜
王 丹,李 琦,*,梁 栋,张烁瑜
(1.河北工业大学电子信息工程学院,天津300401;2.河北工业大学土木与交通学院,天津300401)
0 引言
公路是我国道路交通网中至关重要的构成部分,良好的道路状态是保证公路交通安全的首要条件,如何更有效地规避道路安全威胁成为首要问题。其中路面裂缝就是威胁道路安全的主要因素之一,准确快速获取路面损坏信息已成为道路养护首要任务[1]。目前实际路面裂缝检测主要依靠人工肉眼识别,这种肉眼检测方法具有很多弊端:耗费大量资源与人力成本;效率低危险系数大;检测结果受人为影响,容易发生漏检误检等[2]。因此,借助技术手段对公路路面裂缝实现快速高效准确的检测具有较大的实际需求。
现阶段路面裂缝检测算法主要分为两类,第一类是传统的基于图像处理的裂缝检测方法,首先需通过图像背景差[3]或细节增强法[4]对图像进行预处理,然后借助边缘检测[5]、多尺度分析[6]、多特征融合[7]等方法对路面图像进行分割,得到路面裂缝区域,但受道路上的多种噪声干扰较大。另一类基于深度学习的路面裂缝检测算法在应对路面噪声方面表现良好,它主要使用卷积神经网络(CNN)[8]进行裂缝块状区域分类。文献[9]提出了一种自适应增强卷积神经网络,通过增加残差反向传播层和自适应增强模块提高路面裂缝的检测精度。文献[10]建立了3个路面裂缝识别模型,可有效检测出病害类别,并将结果传递给下一模型进行特征提取,大幅度提高路面裂缝检测效率。文献[11]对不同尺度图像子块的中间层特征编码,并将所获取的局部特征与浅层的全局特征融合,以描述图像多尺度特征。文献[12]利用改进Otsu法解决了分割裂缝信息时对过小信息不敏感以及受背景光照影响较大的问题。
由于基于CNN的路面裂缝检测算法无法做到预测结果与像素的一一对应,近年来,基于全卷积神经网络的语义分割成为主要发展趋势。LONG等[13]提出的全卷积神经网络(FCN)为路面裂缝进行像素尺度的图像分割带来了较大的进展,成为该领域较为先进的方法。文献[14]在其基础上利用4倍上采样的全卷积神经网络对图像做处理,融合了更多的细节信息,但4倍上采样层大大地增加了算法迭代时间和网络结构复杂度。文献[15]利用不同尺寸的池化层进行多尺度特征识别来获取多层特征,解决训练模型匹配关系错误并且无视小物体的问题。BADRINARAYANAN等[16]通过编码网络、解码网络以及一个像素级别的分类层代替FCN编解码器,做到解码器低分辨率特征映射放大特征图,但以牺牲分割性能为代价提高了对占用内存空间的压缩。YU等[17]在原算法基础上采用空洞卷积与FCN结合扩大感受野,一定程度上融合了更大尺度信息而不损失分辨率。然而,目前的路面裂缝检测算法没有充分考虑到全局特征信息,损失了大量图像细节。
针对上述问题,为了探寻准确率更高的路面裂缝检测算法,本文提出了一种更为精确的多尺度全卷积与条件随机场(CRF)结合的方法对路面裂缝检测展开研究。通过对比性能指标发现,相较于经典的全卷积网络,改进后的算法分割效果有显著提高。
1 算法框架
基于VGGNet优异的特征提取能力,本文算法采用以VGG-16为主体框架的FCN-8s网络,并针对提高网络模型检测准确性进行改进。改进算法步骤为:
1) 将VGG-16的池化层pool3、pool4的strides设置为[1,1,1,1],padding设置为SAME,使图像特征信息不因池化层影响而损失,又可保留池化整合的特性。
2) 利用空洞卷积构建多尺度模块,并联三条空洞率分别为1、2、5的空洞卷积通道,将VGG-16的卷积层conv5的输出特征图作为该模块的输入,并将三条通道得到的特征信息进行融合。
3) 增加BN层和PReLU层,删除FCN-8s原有的dropout层,防止过拟合现象并进行特征归一化。
4) 对卷积层输出结果进行反卷积操作,再与pool4节点进行跳跃连接和特征融合。通过选择不同步长的反卷积层对融合结果进行二次反卷积,并与pool3节点进行跳跃连接,以修正层级迭代带来的特征消失现象。
5) 将CRF层与多尺度全卷积网络进行端到端的连接,通过SoftMax层做归一化处理,计算出损失函数并不断迭代,实现网络的全局感知。
算法模型结构如图1所示。为了更清晰地展示本文所提出的网络结构,在图1中省略了VGG-16框架的部分主体结构。
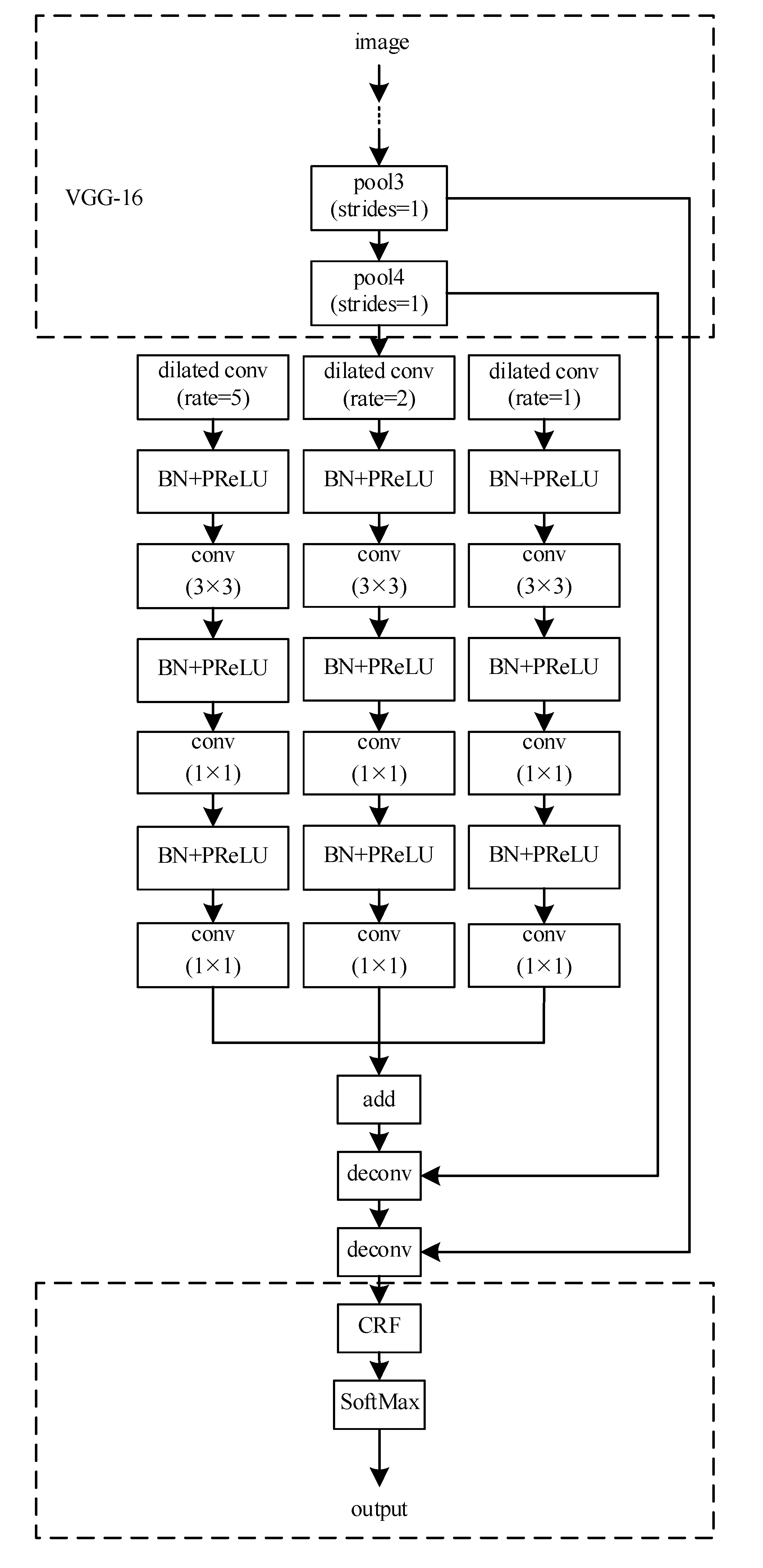
图1 本算法模型结构图Fig.1 Structural diagram of the algorithm model
2 FCN网络改进算法
2.1 具有跳跃连接结构的全卷积神经网络
在CNN算法中,通常由全连接层起到分类器作用,但由于全连接层将输入特征展开为一维向量,无法将分类结果与像素一一对应,损失了输入的空间信息。
本文采用了以VGG-16为主体框架的FCN算法,将全连接层替换为卷积层,构成全卷积神经网络。采用跳跃连接结构将浅层网络特征与深层网络特征融合,利用反卷积层[18]对特征融合结果进行上采样,恢复特征图分辨率。这是由于在网络迭代过程中,较深层的感受野变大,造成细节特征丢失现象,而较浅层的感受野较小,具有更多细节信息。深层特征与浅层特征的融合可提高网络模型的细节捕获能力,有利于共享中间特征。
根据反卷积层位置,可将FCN划分为FCN-32s,FCN-16s,FCN-8s三种模型,模型结构如图2所示。本文算法采用FCN-8s模型。
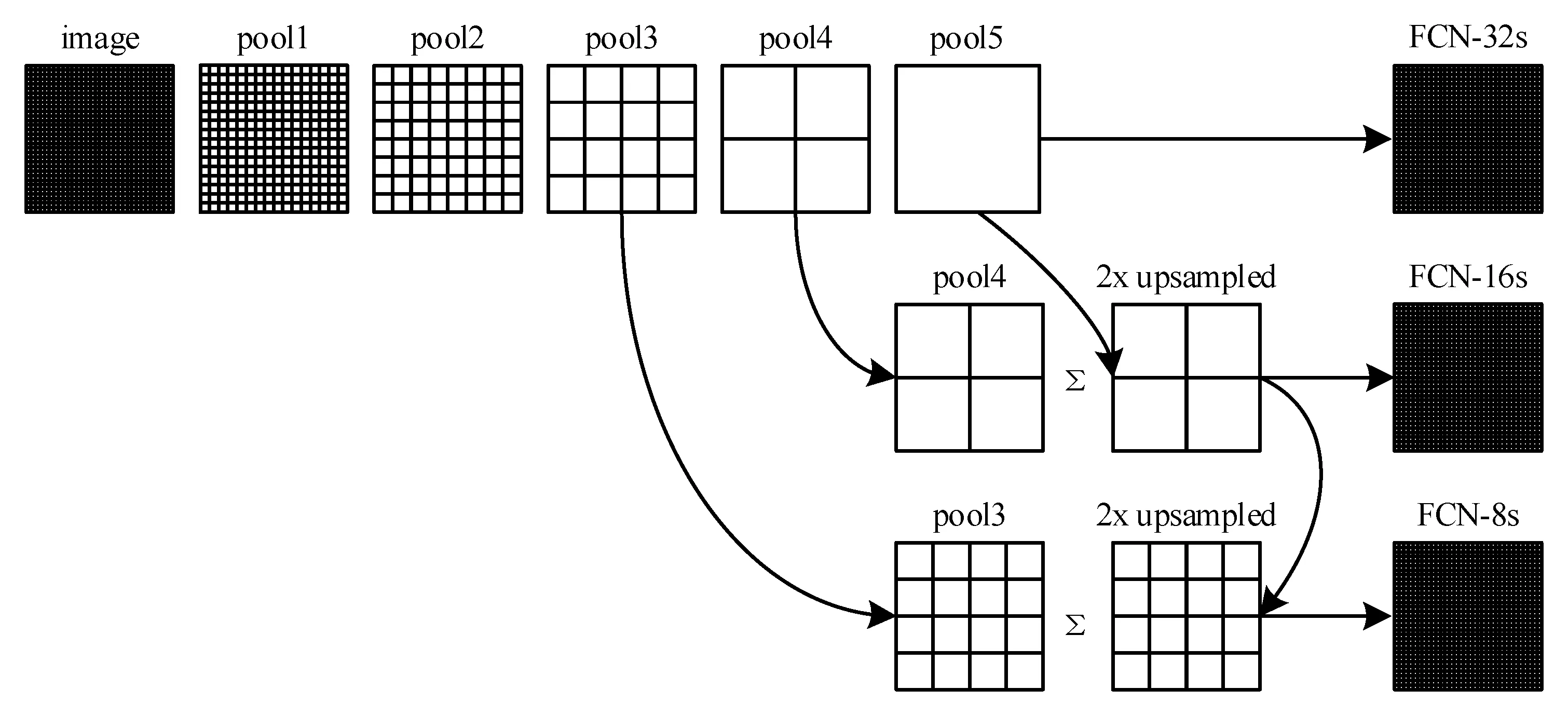
图2 经典FCN模型结构图Fig.2 Structural diagram of classical FCN model
2.2 具有多尺度结构的空洞卷积2.2.1 标准空洞卷积
FCN卷积尺寸的增加使感受野变大,但带来参数计算量的增多。Chen[19]提出了空洞卷积结构,在扩大感受野的同时避免了额外参数计算量的增加。同时,空洞卷积对池化层的替代,有效地减少池化层带来的特征信息损失,保留图像细节。
空洞卷积利用空洞率r控制输出特征图分辨率大小,对输出特征图y[m,n],空洞卷积过程定义如下:
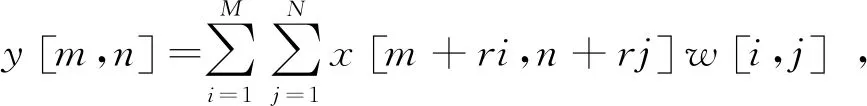
(1)
式中,x[m,n]为输入特征图;w[i,j]为空洞滤波器;m与n分别为特征图像素的长和宽;i与j分别为卷积核的长和宽。空洞率r决定卷积核的采样间隔,当r≥1,表示卷积核之间引入r-1个空洞,当r=1,空洞卷积为正常卷积。空洞卷积结构如图3所示。
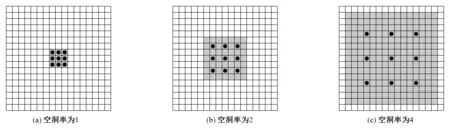
图3 空洞卷积结构Fig.3 Dilated convolution structure
如图3所示,分别为卷积核大小为3×3,空洞率为1、2、4的空洞卷积。当空洞率为r,卷积核大小为k×k时,空洞卷积的感受野扩大为
k+(k+1)(r-1),
(2)
使用stride为1的普通卷积,当卷积层数为Μlayer,感受野大小为
(k-1)×Μlayer+1。
(3)
相比之下,空洞卷积可有效地增大感受野。在图3中,当卷积层数为1时,空洞卷积将普通卷积的感受野由3扩大为7和15,有效地减少了参数计算量。
2.2.2改进多尺度空洞卷积
路面裂缝识别算法多采用单尺度网络结构进行特征提取,忽略了多尺度裂缝特征的感知,造成细小裂缝特征丢失等问题。若再对细小裂缝特征进行重复获取会导致结构冗余[20]。为解决这一问题,本文算法提出利用空洞卷积构建多尺度模块,该模块共包括3条并行通道。
3条通道的空洞率选择应满足彼此间不具有大于1的公约数,则该卷积结构可以避免损失信息的连续性,且需满足
Mi=max[Mi+1+2ri,
Mi+1-2(Mi+1-ri),r],
(4)
式中,ri为第i层的空洞率;Mi为第i层的最大空洞率。当共有n层时,Mn=rn。当卷积核大小为k×k时,要求M2≤k,则该空洞率下的空洞卷积核可以覆盖图像所有空洞[21]。
经多次实验,当空洞率r分别为1、2、5时,网络模型对路面裂缝的学习效果最好,故采用空洞率r分别为1、2、5的三层空洞卷积层,卷积核大小均为3×3。每个尺度为一个独立分支,分别感知不同尺度感受野的信息。然后,将3个空洞卷积的信息进行融合,并传递给下一模块。
一方面,不同的空洞率可控制多尺度模块学习不同尺度的特征,既保留了原有特征信息,又融合了多个尺度的特征信息,解决了模型对细小裂缝信息不敏感的问题。另一方面,并行的多尺度模块避免了卷积层过多带来的结构冗余,减少了参数计算量。多尺度空洞卷积结构如图4所示。
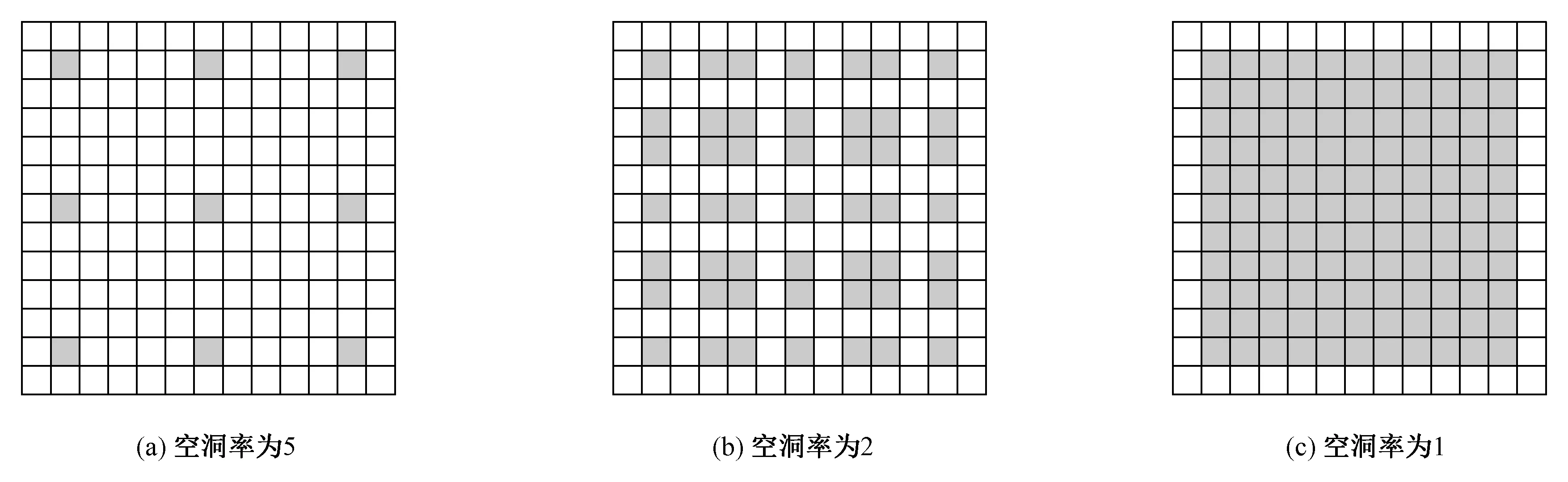
图4 多尺度空洞卷积结构Fig.4 Multiscale dilated convolution structure
2.3 条件随机场
由于SoftMax层中的交叉熵损失函数反映的是每一个像素损失值的和,具有不连续性,并不能充分考虑相邻像素之间的空间一致性。
为了克服SoftMax层的局限性,本文算法将CRF与FCN进行端到端连接,使FCN可有效提取全局信息。这是由于CRF充分考虑到相邻像素标签间的上下文联系,能有效地增强模型的边缘约束能力,让图像在边界处进行分割,避免标签间独立决策导致的准确率限制。
CRF的能量函数[22]为
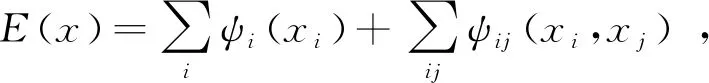
(5)
式中,i、j为像素点;xi、xj为像素i、j对应的标签值。式中第一项为一元势函数,描述前端FCN网络的输出,当P(xi)为像素i的标签分配概率时,
ψi(xi)=-logP(xi),
(6)
式中第二项为二元势函数,描述像素间的空间一致性,表示当i≠j时,邻近的像素点i、j的标签xi、xj之间的相关关系以及观测值对其影响,可理解为当观测值接近,xi和xj属于同一标签的概率较大,反之则较小。二元势函数可用如下公式计算:
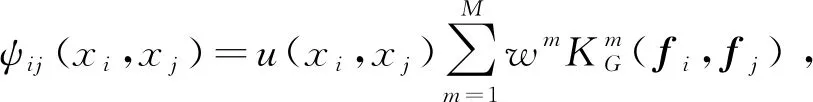
(7)
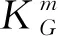
在运算过程中,CRF首先确定模型对像素的预测值,再确定像素值,即该像素的实际类别。接着,对相邻两像素之间的实际类别和像素预测值进行编码,求出依赖关系势能值。当相邻像素间的实际类别相同时,其依赖关系势能较高,由于CRF是完全连接的,所以即使是路径很远的像素间也可共享信息。最后,利用SoftMax层归一化[23]输出结果:
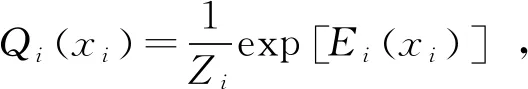
(8)
式中,Zi为归一化因子。该式计算出每个类别的对应概率,输出特征图的预测值。
3 实验结果分析
3.1 模型训练
实验模型搭载Tensorflow深度学习框架,基于Windows操作系统,硬件配置为Intel Core i5 8300H CPU、Nvidia 1050 Ti显卡、8GB内存,软件配置为CUDA 9.0、cuDNN 7.5.1,代码均使用Python 3.5实现。
由于目前的开放数据集如ImageNet、COCO等缺乏路面裂缝数据,本实验训练所用数据集来自于自行采集并标注的1 006幅路面裂缝图像,包括了不同光照、干扰、场景下的数据。为了获得更多数据,通过旋转、镜像、随机裁剪、添加椒盐噪声的方式进行数据增强,将其扩充为8 048幅。测试集为自行采集并标注的200幅路面裂缝图像。均由Nikon D5200相机拍摄,并将图像分辨率压缩为320 pixel×320 pixel。
采集的部分图像数据集如图5所示。
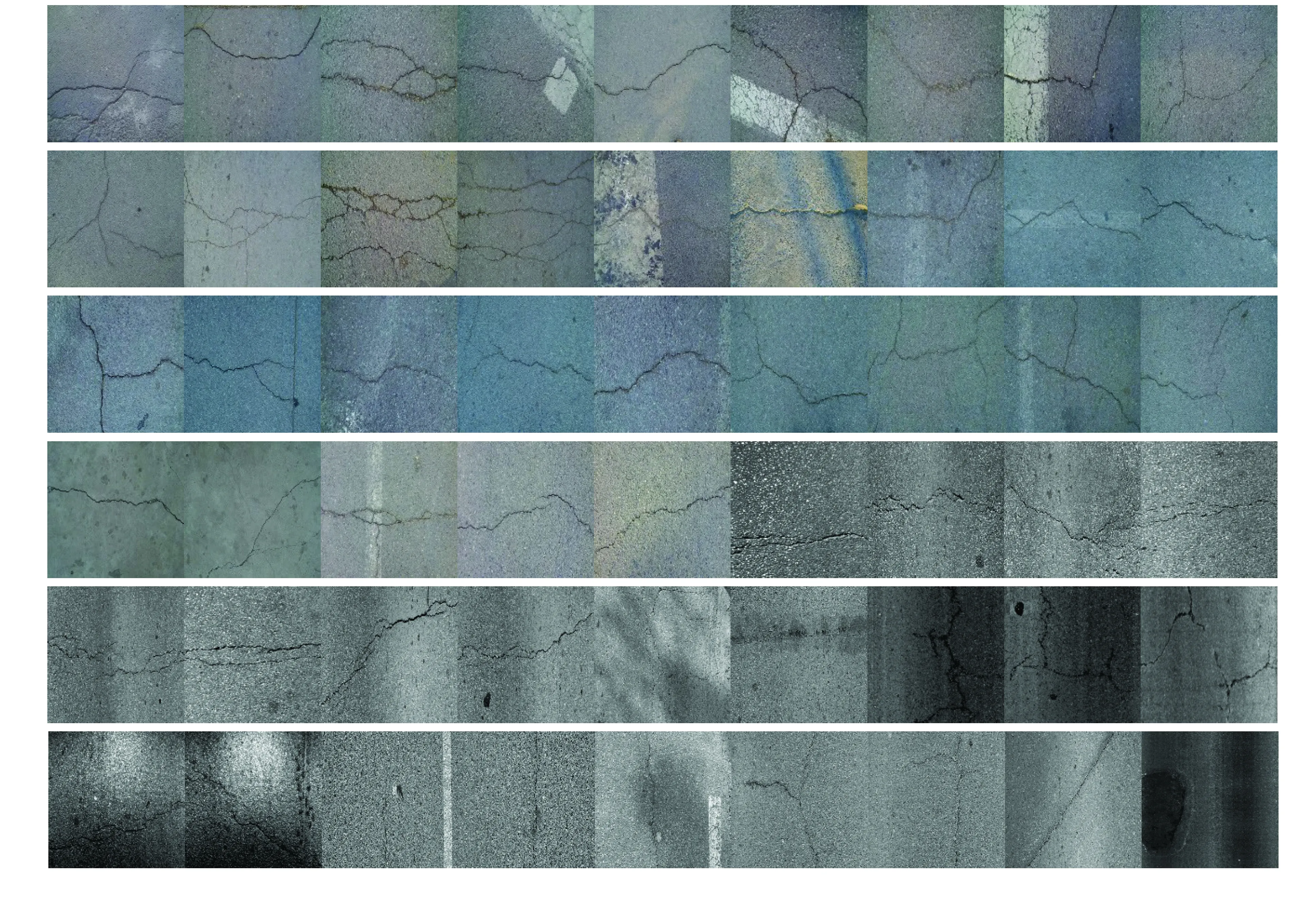
图5 部分图像数据集Fig.5 Part of image data set
图像共标注了2类标签,人为地将裂缝处像素值标注为1,背景处像素值标注为0。加载了VGG-16网络在ImageNet上的参数来初始化模型,减少模型训练时间,并将网络参数设置为:Batch size=2,Learning rate=10-6,Max iteration=105。
3.2 结果分析
实验针对多尺度FCN-8s结合CRF的算法对路面裂缝识别进行研究,在所有训练参数相同,迭代次数均为105次的基础上,对8 048幅路面裂缝数据集进行训练。在训练过程中,本文算法经迭代得到的训练集和验证集损失函数曲线如图6所示。其中:纵坐标为损失值,横坐标为迭代次数。可以看出,在模型训练迭代初期,训练集与测试集的损失函数较大,下降速度较快,此时的训练结果不够真实。经过不断迭代,损失函数下降趋势逐渐平缓,当迭代次数为40 000次时接近收敛,该情况下模型对于各类别之间的判定接近于期望结果。
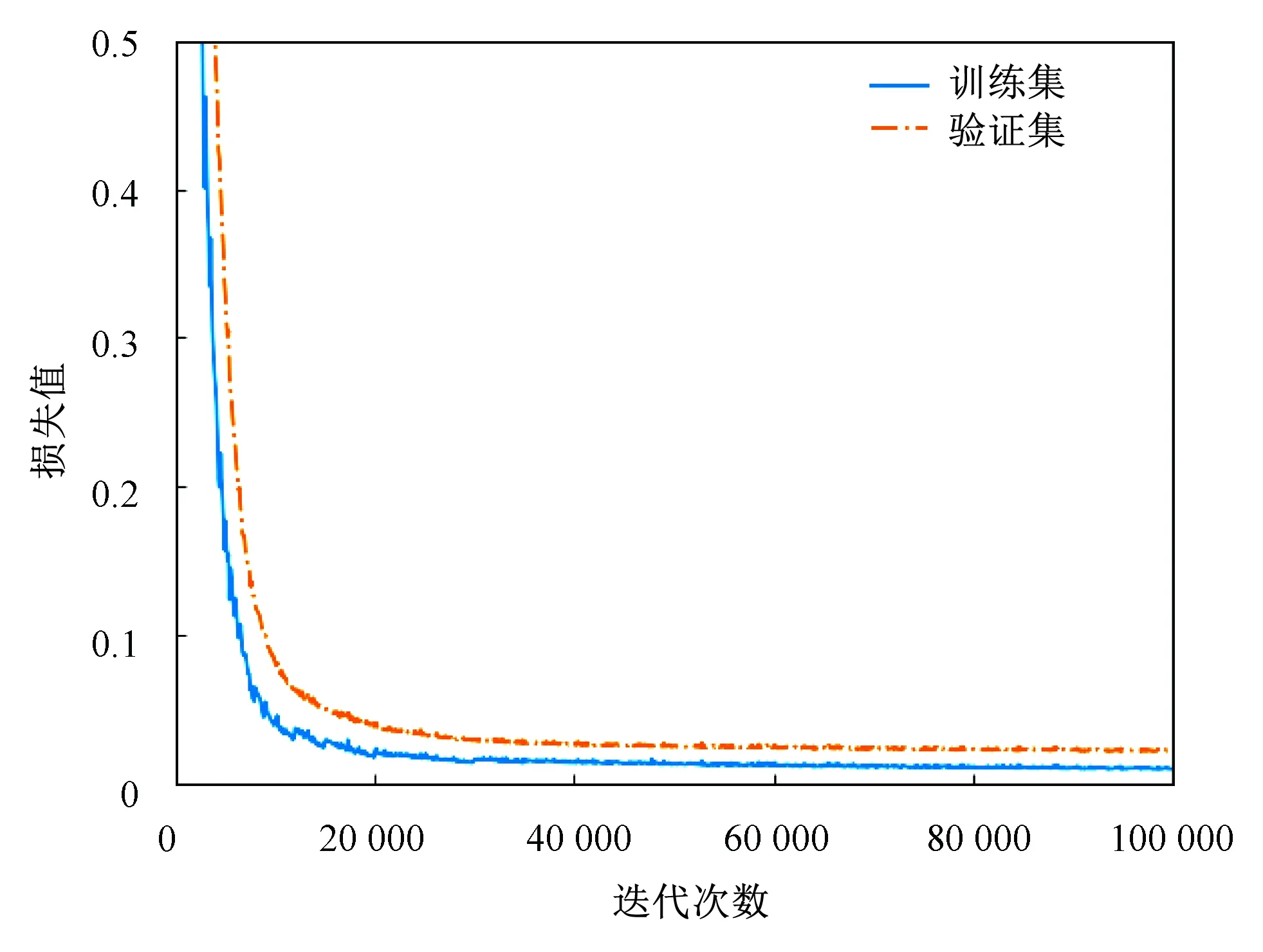
图6 迭代过程中损失函数变化曲线Fig.6 Loss function curve in iteration process
为了更直观地展示算法检测效果,通过对比分析经典算法FCN-16s、FCN-8s和本文多尺度FCN算法、本文多尺度FCN结合CRF算法的性能,利用测试集中几种路面裂缝图片,对比了算法实际的图像分割效果,如图7所示。
通过对比各算法产生的路面裂缝识别效果,由图7(c)可以看出,经典的FCN-16s算法虽然融合了Pool4层,再进行16倍上采样,将深层次特征与浅层次特征进行初步融合,但结果较为平滑,对裂缝形状不够敏感,只能得到裂缝信息的大致轮廓;由图7(d)可以看出,经典的FCN-8s算法依次融合了Pool4层和Pool3层,有效地提升了分类效果,但是仍然损失很多细节特征,对更细小的信息无法准确识别。
由图7(e)可以看出,本文多尺度FCN算法有效地避免了池化层带来的特征损失现象,可同时感知不同尺度大小的裂缝信息,与单尺度网络相比,减少了分割效果的平滑性和模糊性,检测出上述网络中未感知到的细小裂缝,同时避免了非裂缝信息的干扰,不受路面背景中的污渍、凹坑的影响,具有较强的鲁棒性;由图7(f)可以看出,本文多尺度FCN结合CRF的算法与标签图像的细节最相似,具有良好的边缘约束能力,使图像在细小裂缝的边界处进行分割,具有更多的细节信息,表现出良好的分割性能。
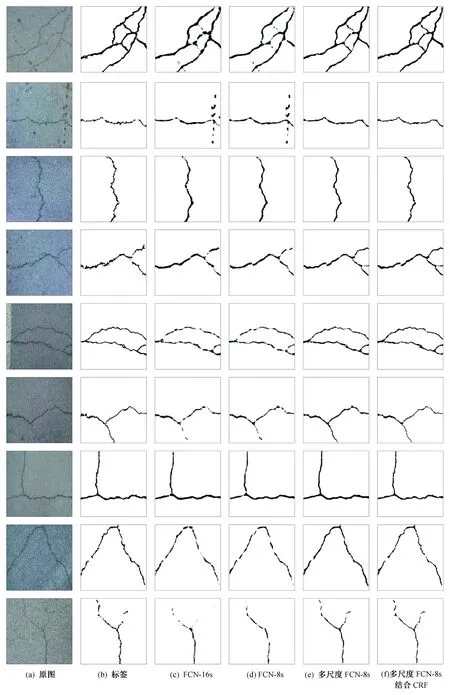
图7 几种算法图像分割效果对比Fig.7 Comparison of image segmentation effects of several algorithms
3.3 性能指标
路面裂缝分割问题可等效为像素的分类问题,为了评估本文算法的性能,通过分析每个像素映射到标签的分类结果,对经典算法FCN-16s、FCN-8s和本文算法多尺度FCN-8s、多尺度FCN-8s与CRF结合算法分别计算了其性能指标。
为了更好地描述性能指标的意义,引入以下4种性能指标的度量标准。True Positive(TP)表示当像素的标签值为1时预测值也为1的情况,False Positive(FP)表示当像素标签值为0时预测值为1的情况,False Negative(FN)表示当像素的标签值为1时预测值为0的情况,True Negative(TN)表示当像素标签值为0时预测值也为0的情况。性能指标的度量标准如表1所示。

表1 性能指标的度量标准Tab.1 Measure standard of performance indicators
利用NTP、NFP、NFN、NTN分别表示TP、FP、FN、TN情况下的像素个数,并用其计算性能指标交并比(IOU)、平均准确率(Mean-Accuracy)、查准率(Precision)、召回率(Recall),根据指标数据评估本文算法的性能。
3.3.1交并比
交并比指预测值与标记值的交叠率,即被预测正确的路面裂缝像素占其他所有像素的比例,是两个标签集合的交集与并集的比值,可以表示为
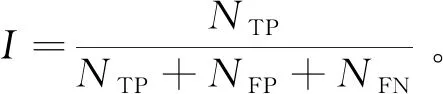
(9)
它反映了模型对判断目标的捕获程度和精确程度,是语义分割、目标检测领域最常用的指标。交并比的值越大,分割结果越好,细节也就越多。如表2所示为4种算法在不同迭代次数下的交并比的值。
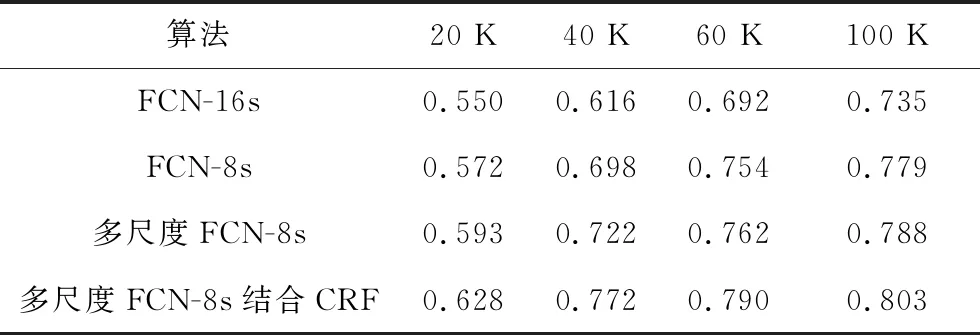
表2 不同迭代次数下的交并比Tab.2 IOU with different iterations
3.3.2平均准确度
准确度为预测值正确的像素占所有像素的比值,可以表示为
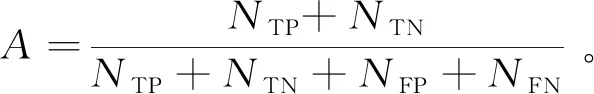
(10)
平均准确度分别计算每个类内被正确分类的路面裂缝像素比例,再求平均值,是准确度的一种提升,可以表示为
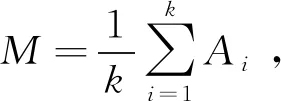
(11)
式中,k为标签类别的数量;Ai为第i类的平均准确度。如表3所示为算法在不同迭代次数下的平均准确度的值。
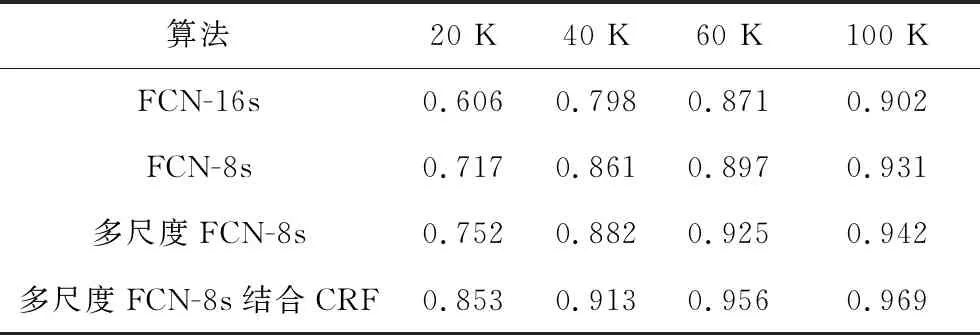
表3 不同迭代次数下的平均准确度Tab.3 Mean accuracy with different iterations
3.3.3查准率
查准率表示预测值为1且真实值也为1的像素在预测值为1的所有像素中所占的比例,即预测正确的路面裂缝像素占所有被预测为路面裂缝的像素的比例,可以表示为
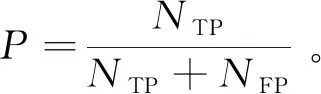
(12)
表4所示为4种算法在不同迭代次数下的查准率的值。

表4 不同迭代次数下的查准率Tab.4 Precision with different iterations
3.3.4召回率
召回率也称为查全率,表示预测值为1且标签值也为1的像素与标签值为1的所有样本像素的比值,即在所有标签值应为路面裂缝的像素中,被预测为路面裂缝的像素所占的比例。可以表示为
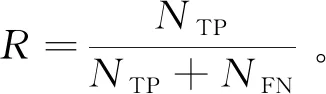
(13)
表5所示为4种算法在不同迭代次数下的召回率的值。

表5 不同迭代次数下的召回率Tab.5 Recall with different iterations
从表5中数据可以看出,在模型迭代105次时,本文多尺度FCN算法的IOU较经典FCN-8s提升了0.96%,平均准确度提升了1.11%,查准率提升了0.69%,召回率提升了1.24%。本文多尺度FCN结合CRF算法与未添加CRF之前的IOU相比提升了1.47%,平均准确度提升了2.71%,查准率提升了2.2%,召回率提升了2.28%。
可以看出本文算法在准确性、对细节的敏感性上均优于传统FCN算法,可有效地提升图像分割的准确性,减少误判漏判情况,性能更优。
4 结语
针对道路养护工作中路面裂缝难以精确定位的需求,提出了一种利用条件随机场结构结合全局特征的多尺度全卷积神经网络路面裂缝检测算法。相较于经典算法主要做了以下三方面的改进:
1)将FCN-8s的反卷积层跳跃结构应用于路面裂缝检测中,并融合浅层特征信息扩充图像细节。相比传统卷积神经网络,此方法可提高模型检测准确度。
2)移除FCN的部分池化层,避免特征损失,提高路面裂缝检测准确率。并提出一种空洞率分别为1、2、5的三条空洞卷积支路并行模块。其中,不同的空洞率可实现对较大裂缝和较小裂缝的多尺度特征感知,弥补了层级迭代带来的细节损失,提高了对不同尺度的裂缝特征的敏感度。空洞卷积可减少前述池化层移除带来的参数计算量,提高训练速度。最终实现准确率提高、模型训练时间减少。
3)设计了一种FCN与CRF端到端连接的层级结构,利用CRF与SoftMax函数结合的方式计算损失函数。充分考虑到相似像素之间标签相同的可能性,有效融合了全局特征,使网络在持续迭代中不断优化训练结果,实现了将分类结果与像素一一对应。
通过将FCN-16s、FCN-8s以及本文改进算法模型性能指标做对比,在迭代十万次后,本文多尺度FCN结合CRF算法的交并比可达到80.3%,平均准确度为96.9%,查准率为69.7%,召回率可达到91.7%,均高于经典网络。该算法较经典FCN算法的路面裂缝识别精确度有显著提高,可以满足实际裂缝识别任务的需求。
