基于三线阵CCD的室内导航方法研究

王 闯，屠晓伟

(1.上海大学 机电工程与自动化学院，上海 200444；2.许昌学院 信息工程学院，河南 许昌 461000)

0 引言

室内移动智能体广泛应用在商业、物流、自动化生产、军事等领域。移动智能体的高精度位置和姿态信息是完成用户指定运行任务的基础，同时也是实现精准运动控制和导航路径规划的前提条件。

室内移动智能体位置和姿态的测量方法主要分为两类：相对定位和绝对定位[1]。相对定位技术通过估测移动智能体相对于起始位置的方向和距离来推断出当前的位置信息。航迹推算法是相对定位技术中的一种经典方法，通过惯性测量单元或测量里程计的方法而实现的航迹推算法既不需要外部信息,也不需要向外发射任何信息，它能够独立工作并且连续不断地为移动智能体提供定位服务。然而，航迹推算法的测量误差会随着时间积累，所以该方法仅满足短时间内的状态估计，无法实现复杂环境下的长时间定位[2]。同时航迹推算法还需要引入初始航向角与位置信息，在实际场景中较难实现。因此，移动智能体位置和姿态的估测更多地依靠绝对定位方法。

在过去几十年，绝对定位受到相关研究者的关注，并取得了重大进展。绝对定位需要测量多个已知位置的参考点来获取移动智能体的位置信息。室外绝对定位技术的典型代表是全球定位系统(Global Positioning System,GPS)，自从GPS投入使用后，室外定位的应用越来越广泛。然而，在城市地区和建筑物内部，建筑物的墙壁和屋顶阻挡了GPS信号传播，使得GPS系统不能在室内正常工作，因此室内绝对定位方法的研究进入了一个快速发展的时期[3]。

在室内绝对定位技术中，基于锚节点的测量方法为室内移动智能体的定位和导航提供了多种选择，例如使用可见光[4]、超声波[5]、Wi-Fi[6]、Ultra Wide Band (UWB)[7]等无线定位技术。然而，这些定位技术往往受到多径效应等因素的干扰，而且绝大多数都不能提供三维的位置和姿态服务，在室内移动智能体的导航应用中存在很大的缺陷。

最近几十年来，光电测量技术发展迅速，相关研究者提出了很多可行的方法。激光雷达主要采用红外激光束以径向视野扫描周围环境，它以其测量精度高、灵活性强、实时性好等特点，已在多种室内环境场合中广泛使用[8]。但是在某些场合下，如在飞机大部件的高精度装配和对接程序中，激光雷达技术很难同时获得移动平台的位置和方向[9]。文献[10]采用基于激光的光电扫描方式测量锚节点的三维坐标，并使用坐标转换算法实现了室内位置和姿态的测量。但该方法需要使用复杂的旋转激光扫描仪器测量室内锚节点的三维坐标，并且激光设备价格昂贵，不便于在室内多个移动智能体情况下大规模使用。

基于电荷耦合器件(CCD)或CMOS的视觉传感器采用非接触的测量方法，可以在不干扰系统的情况下估测出室内移动物体运动参数。视觉传感器具有结构简单、安装方式多元化、探测信息丰富、自身不受外界电磁干扰等优点。文献[11]使用面阵CCD相机来估测室内位置和姿态，但该方案需要分别考虑二维或三维工作情况，从而决定锚节点的使用个数。文献[12]使用面阵相机观测矩形约束信标，然后获得机器人位置和姿态。然而，该系统要求相机的光轴总是指向目标中心点，这使得该方法复杂而笨拙，不适合室内较大工作范围的使用。目前有一些商业现成的设备通过计算机视觉的方法来测量目标的位置和姿态信息[13]，但是这种设备不能提供360°方向的测量，不适合不断变化的室内背景，并且这些设备价格昂贵，更大的测量空间需要更多的相机测量设备，导致整个系统成本开销的增加。

现有的室内位置和姿态的视觉测量方法主要采用面阵CCD或CMOS，较少采用线阵CCD来实现室内移动智能体的位置和姿态的测量。文献[14]使用线阵CCD测量室内移动物体的位置和姿态，然而该方法需要使用多套线阵CCD测量设备，并且只能在较小的室内空间测量位置和姿态。文献[15]提出了一种3D运动跟踪系统，该系统使用多个线性光学传感器阵列，辅以惯性测量单元，在位置和姿态跟踪方面取得了良好的性能。但是该方法需要使用线阵CCD和惯性测量单元分别测量位置和姿态，并且也只能在小范围的室内空间内实现位置和姿态测量。

针对移动智能体在室内导航过程中的位置和姿态问题，本文使用3个线阵CCD和3个柱面透镜设计了一种新型的室内位置姿态传感器，通过三平面相交于空间一点的方法，即可在该传感器上建立传感器坐标系。通过在室内屋顶上布置多个红外LED锚节点，根据位置姿态传感器在室内移动的位置，测量传感器视域范围内锚节点的三维坐标值，获取到至少3个锚节点在传感器坐标系下的三维坐标值后，通过罗德里格矩阵坐标转换算法，即可估测出移动智能体在室内的位置和姿态信息。该方法简单实用，精度高，成本低，适合于室内移动智能体的大规模应用。

1 测量原理

线阵CCD在计算机视觉测量中应用广泛，与面阵CCD或CMOS相比，线阵CCD具有高分辨率和快速的帧速率，在精确坐标测量和动态位置跟踪方面具有突出的优势[16]。

1.1 系统组成和工作原理

一维线阵相机由两个部分组成，一个线阵CCD和一个柱面透镜。柱面透镜用于实现从三维空间到一维成像的投影映射。根据光学的基本原理，来自柱面透镜一侧物点的光线将在另一侧形成线性图像[17]，如图1所示。

图1 一维成像单元投影模型Fig.1 Projection model of the one-dimentional imaging unit

在图1中，线阵CCD和柱面透镜构成一维成像单元(One Dimensional Imaging Unit,ODIU)，来自LED发光点的光线通过柱面透镜将聚焦在焦平面上。为了检测由于LED发光点移动而引起的变化，将线阵CCD图像传感器放置在柱面透镜的焦平面。线阵CCD垂直于柱面透镜的光轴放置，用来检测和标记LED移动时投影线的变化。线阵CCD的中心与柱面透镜光轴的中心上下对照，它们之间的距离是柱面透镜的焦距。LED的投影线垂直于线阵CCD并在CCD上形成脉冲峰值点，经过图像处理后可计算出LED的一维图像坐标。如果线阵CCD上的成像点和柱面透镜的光轴是已知的，则可以计算出包含LED位置的平面。

一条直线和一个不在这条线上的点可以定义一个平面。为了在传感器坐标系下测量LED锚节点的三维坐标，至少需要3个ODIU来存储LED的3个一维图像位置坐标，以重建传感器坐标系下LED的坐标值。如图2所示，3个ODIU的线阵CCD在同一水平面布置，LED的三维坐标可以通过3个平面的相交点来估测。当LED位于传感器的视域范围时候，LED穿过相应的柱面透镜并形成分别垂直于3个线阵CCD的3条投影线，投影线在相应的焦平面上与3个线阵CCD相交形成3个投影点，以此来计算投影线的位置信息。如果确定了每个ODIU中的投影线的交点位置，则就确定了3个投影面，这3个投影面的相交点就是LED锚节点在传感器坐标系的位置。因此，在传感器坐标系下的LED锚节点的三维坐标可以由3个虚拟平面唯一地解析。

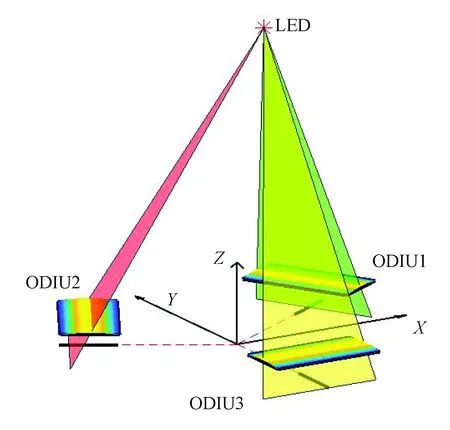
图2 位置姿态传感器原理图Fig.2 Schematic of the position and attitude sensor

同时，将3个线阵CCD感光区域的延长线交点设置为位置姿态传感器坐标系的原点，每个线阵CCD的感光区域都位于传感器坐标系的XY平面上。其中线阵CCD3位于Y轴的负半轴上，而CCD1和CCD2分别位于第一象限和第二象限。

1.2 位置姿态传感器视域

图2中的位置姿态传感器只能测量其视域范围内LED锚节点的三维坐标。同时在室内导航中，传感器的视域对于天花板上的锚节点布局非常重要，传感器坐标系在XY平面上的投影图如图3所示。

图3 传感器在XY平面投影图Fig.3 Projection drawing of the sensor on XY plane

在图3中，线阵CCD光敏元件的感光长度L都等于30 mm。线阵CCD3位于Y轴的负半轴上，将CCD3顺时针旋转120°移动到CCD2的位置，同时将CCD3逆时针旋转120°移动到CCD1的位置。CCD1_In，CCD2_In和CCD3_In是线阵CCD靠近坐标原点的内边缘，它们到原点的距离d都等于60 mm；CCD1_Out，CCD2_Out，CCD3_Out是线阵CCD的外边缘，它们到原点的距离都等于90 mm。a1和b1，a2和b2，a3和b3分别是3个柱面透镜的光轴在XY平面上的投影线，柱面透镜的焦距为50 mm，仿真参数如表1所示。

根据表1，在3个线阵CCD的光敏区域每隔1 mm选择投影点，由于一般室内距离大部分在6 m以内，因此只考虑室内空间的Z坐标值在[0,6 000 mm]范围的情况。图4是根据表1中的参数仿真得到的传感器的视域图。根据图4中的仿真结果，传感器最近的测量距离为300 mm，同时可测量视域随着距离的增加而变大。

表1 仿真参数Tab.1 Simulation parameters

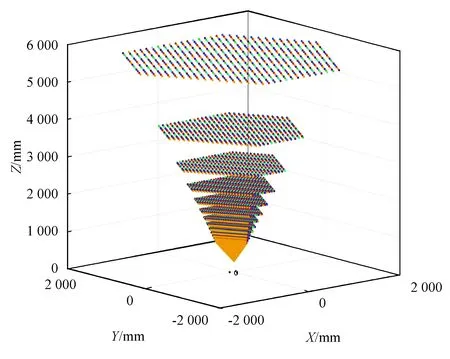
图4 传感器视域图Fig.4 The vision field of the sensor

2 位置和姿态测量算法

在室内位置和姿态测量系统中，有两个不同的坐标系统。一个是室内坐标系，它的坐标原点设在屋内的墙角处。另一个是位置姿态传感器坐标系，它的坐标原点设定在传感器上，如图2所示。

2.1 数学模型

设定3个锚节点A1，A2，A3固定在天花板上，它们在室内坐标系下的坐标分别为A1(X1,Y1,Z1)，A2(X2,Y2,Z2)和A3(X3,Y3,Z3)。同时设定这3个锚节点在传感器坐标系下的坐标值分别为C1(xc1,yc1,zc1),C2(xc2,yc2,zc2)和C2(xc2,yc2,zc2)，根据锚节点在室内坐标系和传感器坐标系下的三维坐标值，列出坐标转换方程来实现从传感器坐标系到室内坐标系的转换，即

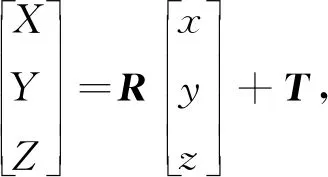
(1)

式(1)建立了锚节点在两个坐标系之间的关系，其中[XYZ]T表示锚节点在室内坐标系下的坐标值，[xyz]T表示锚节点在传感器坐标系下的坐标值，R是3×3旋转矩阵，T=[x0y0z0]T是平移向量。在坐标转换方程中，平移向量T表示传感器坐标系的原点在室内坐标系的位置，旋转矩阵R里面含有传感器坐标系相对于室内坐标系的旋转角度，这些旋转角就是要求的姿态角。

假设传感器坐标系的x轴，y轴和z轴在室内坐标系下的旋转角分别是α、β和γ。设定α为俯仰角，β为滚转角，γ为偏航角。同时定义顺时针方向的旋转角为正，逆时针方向的旋转角为负。根据旋转角，可以得到绕x轴，y轴和z轴转动的旋转矩阵为

定义旋转矩阵R=Ry(β)Rx(α)Rz(γ)，其中α=arcsin(R[2,3]),β=-arctan(R[1,3]/R[3,3]),γ=-arctan(R[2,1]/R[2,2]),R的计算结果为

2.2 罗德里格矩阵坐标转换算法

为了求解式(1)中T和R，至少需要3个锚节点。使用罗德里格矩阵坐标转换算法来求解R和T。在式(1)中，根据转换算法，首先要计算R，然后计算T[18]。

设反对称矩阵S为

(2)

其中，a、b、c是独立参数，R由反对称矩阵S和3×3单位矩阵I组成，即

R=(I-S)-1(I+S)

。

(3)

由式(1)可以列出3个方程，第j个锚节点的方程分别减去第i个锚节点的方程，可以消除平移向量，然后得到

(4)

把式(3)代入(4)，可得到

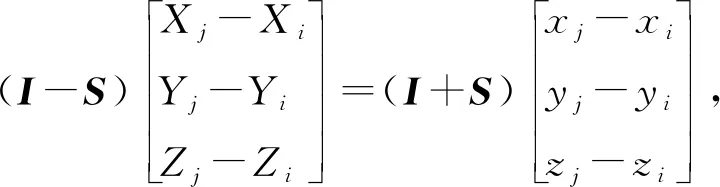
(5)

将式(2)代入式(5)，然后提取a，b和c并表示成

(6)

其中,Xij=Xj-Xi,Yij=Yj-Yi,Zij=Zj-Zi,xij=xj-xi,yij=yj-yi,zij=zj-zi。

在式(6)中，左边的系数矩阵是一个奇异矩阵，在只有两个独立方程的情况下不能求解a、b和c这3个参数，再使用锚节点k和锚节点i可以得到

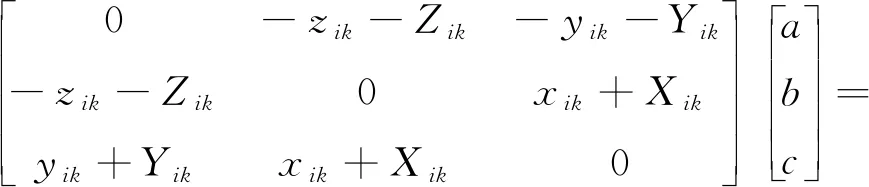
(7)

然后结合式(6)和(7)，得到

。

(8)

由式(8)可以计算出a、b、c三个参数，再根据式(2)和(3)可求出旋转矩阵R，然后把R代入式(1)可以计算出平移向量T。经过上面的步骤，就可以求出平移向量T和旋转矩阵R，这两个参数分别包含有位置姿态传感器在室内坐标系下的位置和姿态角。

2.3 多个公共点情况的坐标转换算法

如果位置姿态传感器在其视域范围内检测到3个以上的锚节点(n>3)，由多个锚节点估测旋转矩阵和平移矩阵的问题就可以转换为最小二乘问题。当两个坐标系中存在有多个公共点，根据式(8)，列出误差方程为

V3(n-1)×1=A3(n-1)×3·X3×1-L3(n-1)×1,

(9)

式中，X3×1=[abc]T，矩阵A3(n-1)×3和L3(n-1)×1为

L3(n-1)×1=[Xij-xijYij-yijZij-zij…
Xin-xinYin-yinZin-zin]T。

根据最小二乘原理，可得到式(9)的最优解为X=(AT·A)-1·AT·L。

根据最优解，即可求出在多个公共点情况下，罗德里格矩阵坐标转换算法中的3个独立参数a、b、c。由这3个参数和式(2)、(3)即可求出多个公共点情况下的旋转矩阵R。

考虑到公共点在空间坐标系的测量误差，根据式(1)列出其误差方程，即

(10)

令ae=[XYZ]T，be=[xyz]T,则式(10)可以简化为E=ae-R·be-T。

由最小二乘的矩阵推导，在满足

min(‖ae-R·be-T‖2)2

(11)

条件下，可使误差矩阵E达到最小，其中‖‖2表示二阶范数。将式(11)展开，可得

min(‖ae-R·be-T‖2)2=

min((ae-R·be-T)T·(ae-R·be-T)),

(12)

将式(12)对平移向量T求偏导，并令其偏导值等于零，求出误差矩阵达到最小时，平移向量的最优解为

(13)

根据式(13)，计算出3个以上的公共点分别在两个坐标系的重心坐标，然后使用多个公共点情况下求出的旋转矩阵R，即可求出多个公共点情况下的平移向量T。

3 仿真结果与分析

图5是室内位置姿态测量系统的仿真模型，尺寸为5 000 mm×5 000 mm×3 000 mm，25个红外LED作为锚节点固定在天花板上，锚节点在室内坐标系下的坐标值如表2所示。

表2 室内锚节点坐标值Tab.2 The coordinate of indoor anchorsmm

图5 室内导航系统模型Fig.5 System model for indoor navigation

位置姿态传感器在室内移动，从测量点P1，经过P2、P3、P4、P5、P6、P7、P8、P9、P10，最后回到P1，如图5所示。

设定传感器在室内坐标系下P1的位置[1 000 mm, 1 000 mm,300 mm]，俯仰角α=0°，滚转角β= 0°，偏航角γ= 0°，因此平移向量T=[1 000 mm,1 000 mm,300 mm]。根据各个锚节点在传感器上3个线阵CCD的投影点位置，计算后可知A1，A2，A6，A7这4个锚节点在传感器的视域范围内，求出锚节点A1在线阵CCD1，CCD2和CCD3上的投影点在传感器坐标系下的坐标值分别为m1，m2，m3；A2，A6和A7在线阵CCD1，CCD2和CCD3上的投影点在传感器坐标系下的坐标值分别为n1，n2，n3；p1，p2，p3；q1，q2，q3，如表3所示。

表3 传感器坐标系下的相交点坐标Tab.3 The intersection in sensor coordinate system mm

根据表1中位置姿态传感器的仿真参数，将锚节点A1，A2，A6，A7在传感器坐标系下的交点坐标m1，m2，m3，n1，n2，n3，p1，p2，p3和q1，q2，q3与仿真参数表1相对比，这些交点坐标全部都位于CCD1,CCD2和CCD3在传感器坐标系下的可测量范围内。

根据表3中锚节点A1在3个线阵CCD上的坐标值m1，m2，m3，求出A1在传感器坐标系下的坐标值为a1=[-499.99 mm,-499.99 mm,2 699.99 mm]。同理根据n1，n2，n3，p1，p2，p3，q1，q2，q3可以求出锚节点A2，A6，A7在传感器坐标系下的坐标值为a2=[-499.99 mm,499.99 mm,2 699.99 mm]和a6=[499.99 mm,-499.99 mm,2 699.99 mm]，a7=[499.99 mm,499.99 mm,2699.99 mm]，如表4所示。

根据4个锚节点A1，A2，A6，A7在表2中室内坐标系下的坐标值和表4中传感器坐标系下的坐标值，使用第2节的罗德里格矩阵坐标转换算法同时求解在位置P1时传感器的位置和姿态。

表4 传感器坐标系下A1，A2，A6，A7坐标值Tab.4 The coordinate of A1,A2,A6,A7 in sensor coordinate system mm

同理，由P2，P3，P4，P5，P6，P7，P8，P9，P10在室内设定的位置和姿态的，按照传感器在位置P1的计算过程和方法，可分别计算出其他9种情况下可以估测到的锚节点，如表5所示。

表5 不同位置可估测的锚节点Tab.5 Measurable anchors at different location

由表5中P2，P3，P4，P5，P6，P7，P8，P9，P10这9个位置可测量到的锚节点，按照位置P1时候的求解方法，分别求出不同位置时可估测到的锚节点在传感器坐标系下的坐标，使用第2节的罗德里格矩阵坐标转换算法，将不同位置时估测出的位置和姿态列于表6中。

将表6中10次计算结果在x，y，z轴3个方向的测量误差值进行最大误差和平均误差统计，并根据平均误差求出标准差，如表7所示。

同时对表6中10次计算结果在俯仰角α，滚转角β，偏航角γ的测量误差值进行最大误差和平均误差统计，并根据平均误差求出标准差，如表8所示。

表6 传感器在各测量点的位置和姿态Tab.6 The position and attitude of the sensor at different measurement point

由表7和表8的测量误差评估结果，将本文提出的方法与文献[9]的方法相对比。本文的测量误差小于文献[9]的方法，如表9所示，表明本文提出的位置姿态传感器在室内导航中的可行性和高精确性。

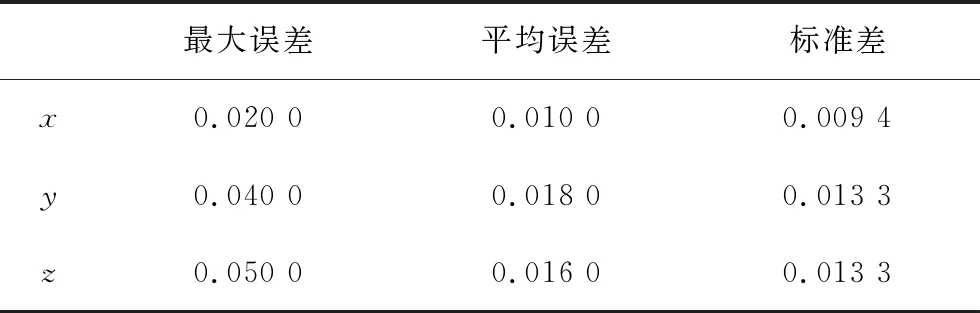
表7 位置测量误差Tab.7 Position measurement error mm

表8 姿态测量误差Tab.8 Attitude measurement error (°)

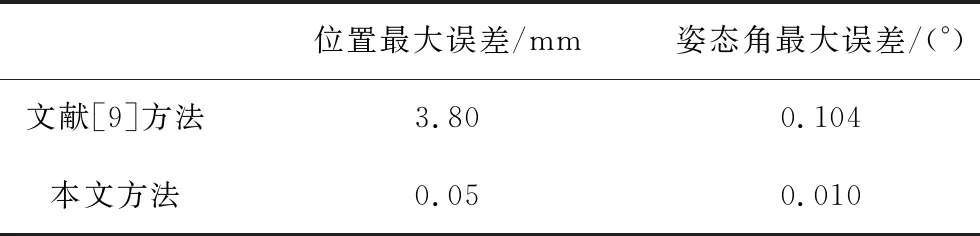
表9 两种测量方法的误差比较Tab.9 Error comparison between two measurement methods

4 结论和展望

本文使用3个线阵CCD和3个柱面透镜设计了一种新型的室内位置姿态传感器，在估测出至少3个锚节点在传感器坐标系下的坐标之后，使用罗德里格矩阵坐标转换算法同时估测出该传感器在室内的位置和姿态。位置姿态传感器不需要考虑平行或倾斜的工作情况，并且与传统的使用3个锚点仅能估测位置的室内导航方法相比，本文提出的方法不仅可以估测传感器在室内的位置，还可以同时估测传感器在二维情况下的航向或三维情况下的姿态。并且在室内导航过程中，传感器的使用个数不受限制。本文提出的方法部署成本低，易于室内大范围扩展使用，仿真结果表明了该方法的可行性和高精度特性。

搭建实物平台是接下来的工作，同时为了提高位置和姿态测量的实时性，位置姿态传感器高速同步曝光多个LED锚节点也是接下来的工作重点。