一种翻滚非合作航天器抵近绕飞避障轨迹规划和跟踪控制方法

黄宇嵩， 田 栋， 李洪珏， 焦荣惠， 李 斐

1. 中国空间技术研究院通信与导航总体部, 北京 100094 2. 国家航天局卫星通信系统创新中心， 北京 100094 3. 北京航空航天大学, 北京 100191

0 引 言

非合作航天器抵近、绕飞和避障控制是开展空间近距离交会对接、航天器在轨加注、失效航天器离轨、空间碎片清理等在轨服务任务的核心技术之一[1-3].随着航天技术的不断发展，空间飞行器的结构、组成日趋复杂，性能、技术水平不断提高，人们对航天器在轨服务的需求越来越强，现有的绝大多数在轨服务目标航天器基本上属于非合作航天器，因此，对空间非合作航天器的无人自主在轨服务是未来重要的发展方向[4].

针对空间翻滚目标相对绕飞问题，文献[5]利用滑模控制和人工势函数理论设计两种快速绕飞避碰控制器以实现对目标的安全快速绕飞.文献[6]采用基于旋量、对偶四元数的方法建立了相对动力学模型，以翻滚航天器为对象进行了相对绕飞的对偶双环滑模控制器设计，实现对目标的恒定距离和姿态同步绕飞仿真验证.文献[7]在常值推力作用假设下进行了相对运动的解析求解，采用模型预测的方法获得航天器相对位置和相对速度的预期偏差.通过广义逆变换构造了关于预期偏差的最小范数、最小二乘全状态反馈控制器，实现了对空间目标的轨道交会、相对悬停保持和循迹绕飞.文献[8]提出一种用于非合作目标惯性指向轴位置捕获的绕飞方法，同时采用扇形轨迹和直线轨迹设计了两类接近轨迹规划策略，以及使追踪航天器x轴始终指向目标航天器的姿态指向控制律.文献[9]基于二阶滑模控制算法设计了相对位置与姿态耦合的自适应控制器，建立了两航天器对接端口间相对位置与姿态耦合的动力学模型，利用李雅普诺夫方法证明了有界干扰下的闭环系统稳定性，并对收敛时间的上界进行了估计.

本文针对非合作航天器抵近、绕飞和避障问题，以抵近轨迹的燃料和时间最优为目标函数，结合抵近过程的动力学和路径等约束进行轨迹规划，最后采用高斯伪谱法对连续最优控制问题进行离散转化，对转化后的非线性规划问题进行求解，得到最优抵近与绕飞路径.同时基于轨道和姿态协同的六自由度轨迹跟踪误差模型，设计了全状态反馈轨迹跟踪控制律，并对控制过程进行了闭环仿真验证，表明了姿轨耦合轨迹跟踪控制律的有效性和稳定性.

1 非合作航天器抵近绕飞相对运动建模

在研究非合作航天器抵近绕飞的控制问题时，由于在抵近过程中有服务航天器视线指向、抵近后的绕飞和对接面相对静止等要求，在进行抵近控制时不可避免的涉及到服务航天器轨道和姿态的协同控制，这就要求相对运动模型包含两个航天器的相对轨道和姿态信息.

1.1 轨道动力学模型

为了方便论述，下文称非合作航天器为目标器，称服务航天器为追踪器.假定目标器和追踪器均运行在近圆轨道上，目标器的轨道坐标系原点在卫星的质心，x轴指向飞行速度方向，z轴指向地心，y轴按右手法则确定，垂直于轨道平面，如图1.

图1 目标器轨道坐标系Fig.1 Orbital coordinate system of the Target

假设追踪器与目标器的距离远小于其轨道半径，忽略外界摄动加速度影响，可得相对运动C-W方程[10]

(1)

式中，x、y、z分别为追踪器在目标器轨道坐标系下的位置坐标，Ω为目标器轨道角速度，ax、ay、az分别为追踪器控制加速度分量.

由于目标器与追踪器相对距离远远小于轨道高度，所以可近似认为目标器与追踪器轨道坐标系重合.抵近的末端条件一般是追踪器与目标器某特征部位保持一定距离和相对姿态，在目标器特征部位本体坐标系下

(2)

式中，xb、yb、zb分别为追踪器在目标器特征部位本体坐标系下的位置坐标，Lob为本体系到轨道系的坐标变换矩阵，代入式(1)，可得非合作航天器特征部位本体坐标系下的相对轨道动力学方程.

1.2 姿态动力学模型

忽略空间干扰力矩，追踪器的姿态动力学方程为[10]

(3)

式中，Jc为追踪器的惯量矩阵，ωc=[ωcxωcyωcz]T为追踪器的本体角速度，Tc=[TxTyTz]T为追踪器的控制力矩.

同时，目标器的姿态动力学方程为

(4)

式中，Jt为目标器的惯量矩阵，ωt=[ωtxωtyωtz]T为目标器的本体角速度.

目标器相对于追踪器的相对角速度ωe=[ωexωeyωez]T，可由下式求得

(5)

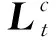
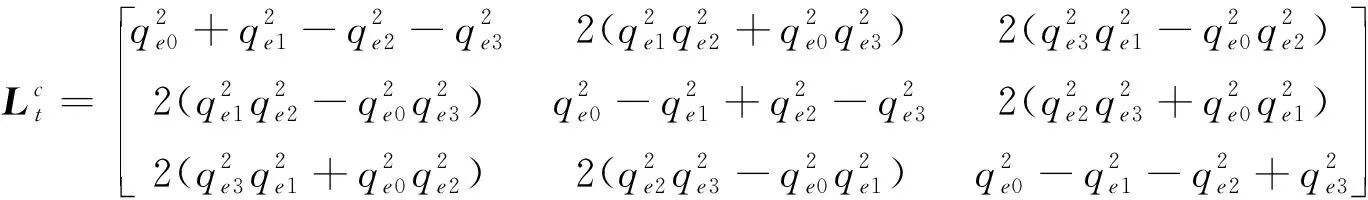
(6)

式中，qe=[qe0qe1qe2qe3]T为目标器相对于追踪器的误差四元数.

两颗卫星的相对姿态运动学方程为[11]

(7)

2 基于高斯伪谱法的轨迹规划问题建模

假设翻滚目标航天器旋转轴不在飞行方向上，且旋转轴方向上不适合开展在轨服务工作，则服务航天器需从其它面进行抵近，并绕目标器进行与目标相同角速度且相对距离不变的面对面绕飞运动，同时保持相同角速度自旋，即可保持相对静止，但需提供长期的指向目标自转轴的向心力才能维持面对面绕飞状态，如图2所示.

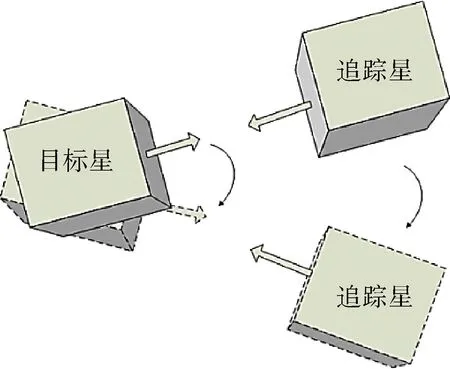
图2 非合作航天器抵近绕飞策略Fig.2 The strategy for non-cooperative spacecraft approach and flying-around

首先构造连续最优控制问题，考虑抵近过程规避障碍物情况，根据非合作航天器抵近绕飞动力学模型，即动力学约束，选取20个状态量如下:

qc1qc2qc3qt0qt1qt2qt3]T

(8)

选取6个控制量如下

(9)

6个控制量约束为|u(i)|≤1,i=1,2,…,6，绕飞半径为r，则位置约束为x2+y2+z2≥r2，设障碍物在目标器本体系下的位置坐标为xb、yb、zb，则规避障碍物约束为

(x-xo)2+(y-yo)2+(z-zo)2≥R2

(10)

其中R为障碍物的等效半径.

轨迹规划的始端约束为X0=X(0)，要求抵近目标器后进行一定距离的绕飞，因此轨迹规划的末端位置约束为

(11)

式中，dtx、dty、dtz为目标器对接点在其本体系下的坐标.xf、yf、zf为末端追踪器在目标器轨道坐标系下的坐标.

抵近阶段结束时的速度约束需达到的绕飞条件为

(12)

要求抵近阶段结束后，两航天器姿态相同，以便下一时刻实现面对面绕飞，因此ωt=ωc，qt=qc.

非合作航天器抵近与绕飞轨迹规划性能指标为

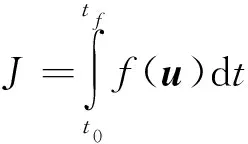
(13)

这里采用时间和燃料多目标优化，则

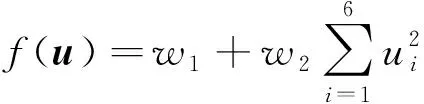
(14)

式中，w1和w2分别为时间和燃料的权重.

综合式(8)～(14)得到非合作航天器抵近、绕飞和避障最优控制问题的描述，采用高斯伪谱法将连续变化的状态量和控制量在有限个数的时间点进行离散，用这些离散点上的Lagrange差值多项式近似表达状态量和控制量函数，再利用Gauss数值积分将积分约束转化为代数求和约束，最终将最优控制问题转化为非线性规划问题，最后采用序列二次规划方法进行求解.

3 轨迹跟踪误差建模与跟踪控制律设计

通过轨迹规划，得到离散时间点的状态量和控制量，以规划的轨迹为目标，基于相对轨道和姿态误差动力学模型设计控制律，使追踪器自主跟踪上规划好的轨迹，实现对非合作航天器的抵近、绕飞和避障.

3.1 六自由度轨迹跟踪误差动力学模型

设ρ=[ρxρyρz]T为追踪器相对于目标器的位置矢量在目标器轨道系下的分量，设ρd=[ρxdρydρzd]T为追踪器在目标器本体系中的期望位置矢量在目标器轨道系下的分量，则可定义相对位置误差为er=ρ-ρd，带入式(1)可得相对轨道误差动力学方程为

(15)

式中

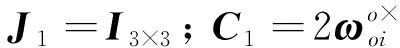
(16)

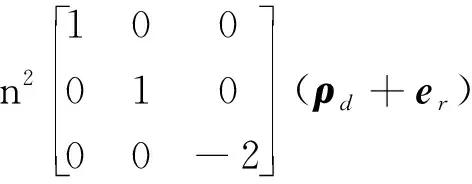
(17)

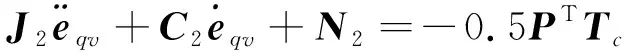
(18)

式中

(19)

(20)

(21)

式中

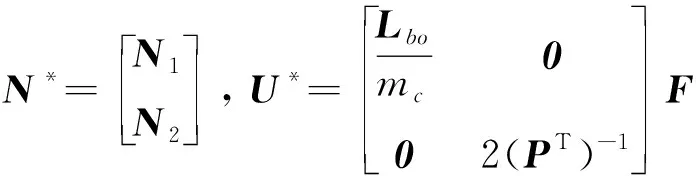
(22)

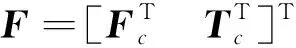
(23)

3.2 基于六自由度误差的控制律设计

以第2章求解出的离散轨迹点为基础，采用插值方法得到近似连续的状态量和控制量，针对相对位置偏差和姿态偏差设计如下全状态反馈控制律，得出修正偏差的控制量，实现对追踪器的轨道和姿态耦合控制

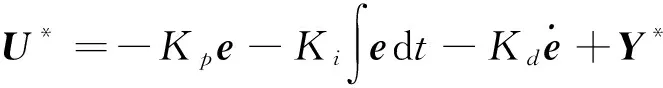
(24)

由式(22)和(24)可得

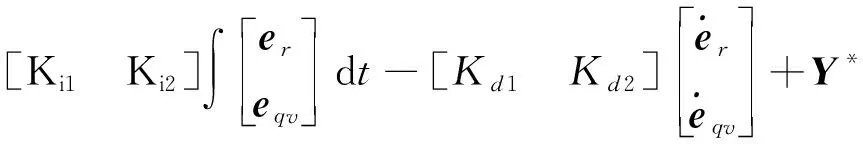
(25)

4 仿真与分析

4.1 轨迹规划仿真结果与分析

按照最复杂工作进行轨迹规划仿真验证，目标器旋转轴不在飞行方向上，服务航天器抵近后需对目标进行面对面绕飞，且途中需规避障碍物.追踪器和目标器的轨道、姿态初始参数如表1所示，动力学参数如表2所示.追踪器在目标器本体系下初始位置为(10.0，0.0，0.0) m，停泊绕飞位置为(-3.0，0.0，0.0) m，障碍物大小为(2.0，2.0，2.0) m，障碍物在目标器本体系下位置为(-6.0，0.0，0.0) m.高斯伪谱法的节点个数设置为20.

表1 追踪器和目标器的轨道、姿态初始参数Tab.1 Initial attitude and orbit parameters of the Chaser and Target

表2 追踪器和目标器的动力学参数Tab.2 Dynamic parameters of the Chaser and Target

经过仿真计算，完成追踪器抵近绕飞轨迹规划，目标器本体系下两器的相对位置和相对速度的变化曲线如图3所示.追踪器和目标器的相对角速度和欧拉角如图4所示.

图3 目标器本体坐标系下的相对位置和速度Fig.3 The relative positions and velocities of the Chaser and Target in the body coordinate system of the Target

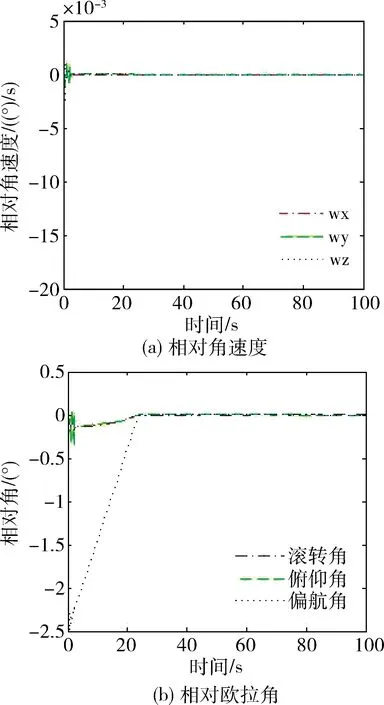
图4 追踪器和目标器的相对姿态Fig.4 The relative attitudes of the Chaser and Target

追踪器在目标器轨道坐标系和本体坐标系下规避障碍物，抵近并对目标器进行面对面绕飞的相对运动轨迹如图5所示.

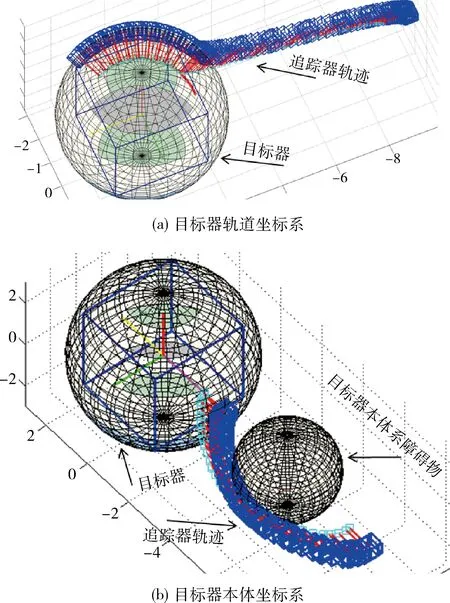
图5 追踪器抵近绕飞目标器的相对运动轨迹Fig.5 The relative trajectories of the Target approach and flying-around

从轨迹规划仿真结果看，追踪器规避障碍物抵近目标后，建立了距离一定速度一定的绕飞轨迹，位置和姿态稳定后，相对位置精度<0.1 m，相对速度精度<0.01 m/s，并保持与目标一致的慢旋姿态，相对姿态精度<0.1°，相对姿态稳定性(角速度)<0.005(°)/s，与目标器保持相对静止状态.

4.2 轨迹跟踪控制仿真结果与分析

基于轨迹规划结果，进行非合作航天器抵近、避障、绕飞的闭环控制仿真，首先根据相对运动敏感器测量到的目标器当前的实测相对位置和姿态，将规划好的抵近轨迹进行插值，得到当前的期望相对位置和姿态，作差后得到控制偏差，采用3.2节设计的轨迹跟踪控制律，根据跟踪偏差计算得到服务航天器的控制力和力矩，闭环仿真原理如图6所示.

轨迹跟踪控制律的(Kp1，Ki1，Kd1)分别取450，50，600，(Kp2，Ki2，Kd2)分别取400，1，400.经过闭环仿真计算，在目标器本体坐标系下的轨迹跟踪位置和速度偏差如图6所示，位置跟踪精度在<±0.01 m，速度跟踪精度<±0.005 m/s.在追踪器本体系下姿态跟踪偏差如图7所示，姿态跟踪精度<±0.01°，角速度跟踪精度<±0.001(°)/s.

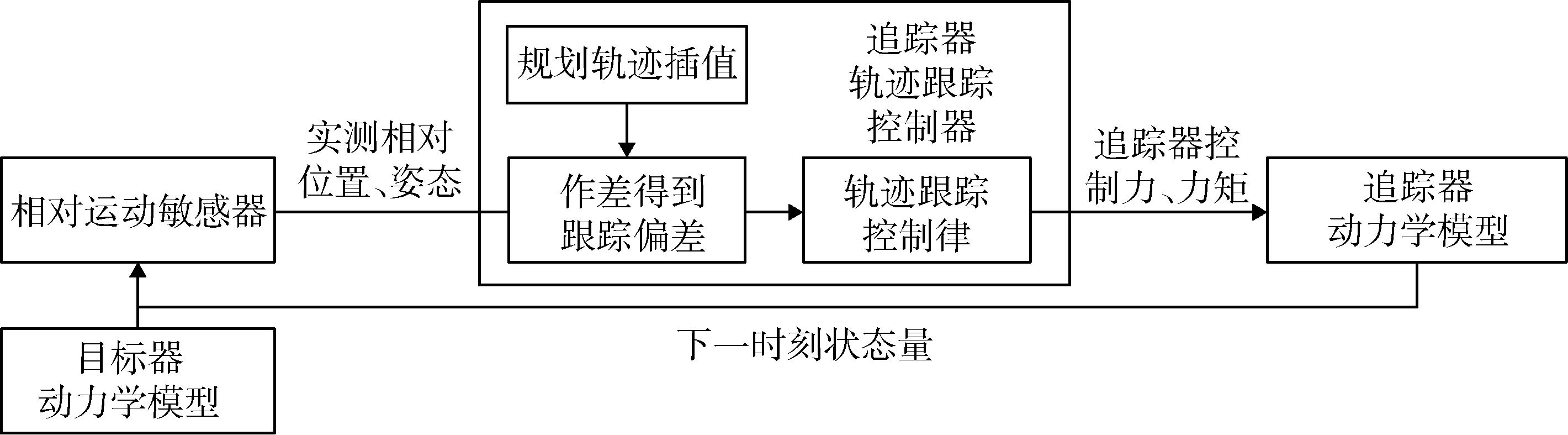
图6 轨迹跟踪控制闭环仿真原理框图Fig.6 Closed-loop control simulation for trajectory tracking

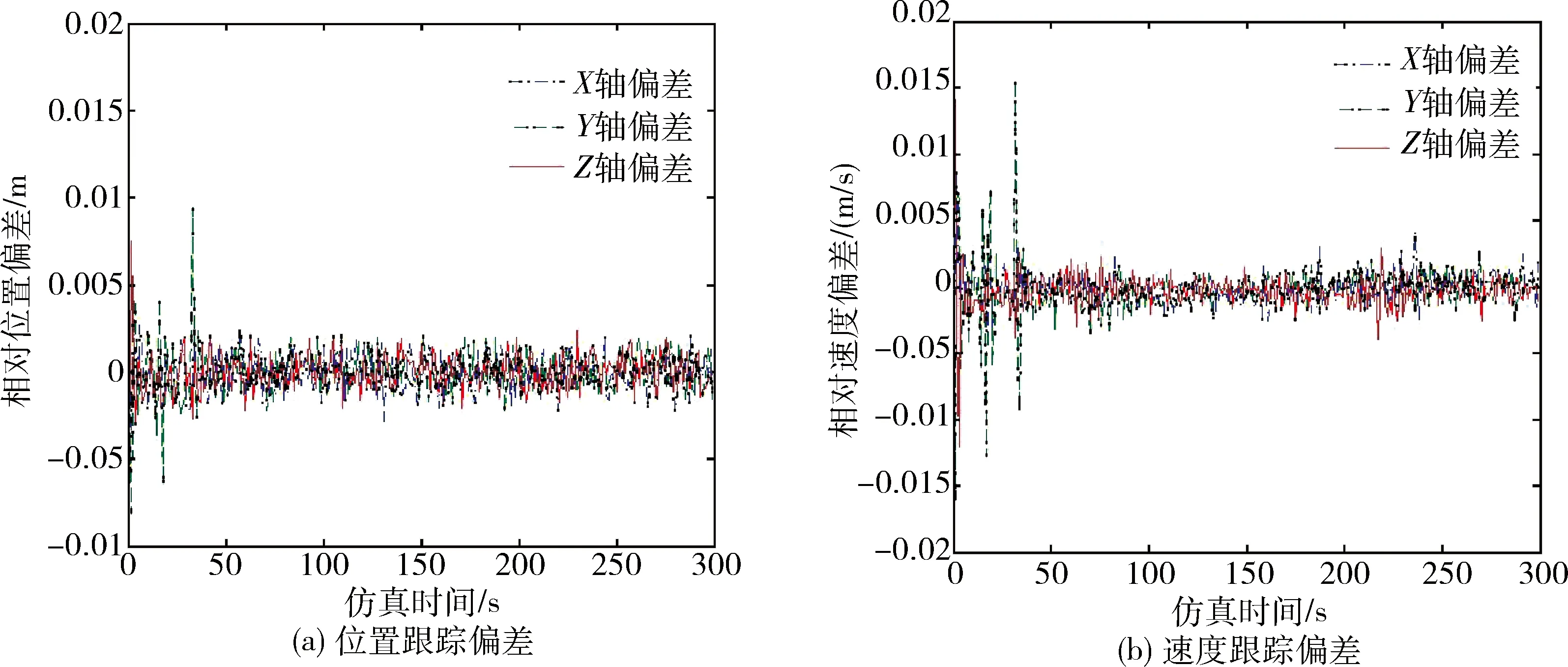
图7 轨迹跟踪控制位置和速度偏差Fig.7 The positions and velocities deviation of trajectory tracking

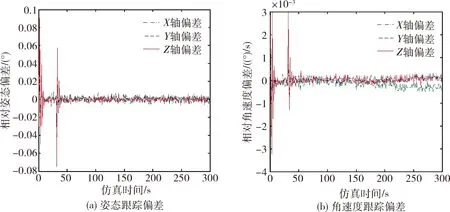
图8 轨迹跟踪控制姿态和角速度偏差Fig.8 The attitude and angular velocity deviations of trajectory tracking

5 结 论

文章针对无人在轨服务任务中非合作航天器抵近、绕飞和避障问题，进行了轨道和姿态相对运动建模，然后以抵近轨迹的燃料和时间最优为目标函数，考虑规避障碍物情况，结合追踪器和目标器相对轨道和姿态动力学和路径等约束条件进行了轨迹规划，最后采用高斯伪谱法对最优控制问题进行了离散转化，对转化后的非线性规划问题进行了仿真求解，得到一定精度的最优轨迹.同时基于六自由度轨迹跟踪误差模型，设计了全状态反馈轨迹跟踪控制律，并对轨迹跟踪控制过程进行了闭环数字仿真，结果表明了非合作航天器抵近绕飞轨迹规划和跟踪控制方法的有效性和稳定性.