太阳同步冻结轨道星座保持与捕获
2021-07-28叶立军王静吉宝音贺西尹海宁刘付成
叶立军, 王静吉, 宝音贺西, 尹海宁, 刘付成
1. 清华大学 航天航空学院, 北京 100084 2. 上海航天控制技术研究所, 上海 201109 3. 上海市空间智能控制技术重点实验室, 上海 201109 4. 上海市航天技术研究院, 上海 201109
0 引 言
太阳同步冻结轨道星座是一种由太阳同步冻结轨道卫星组成的星座,不仅可以实现对地球上任一地区不同太阳光照条件下的观测,而且其在同一纬度上其轨道高度保持不变,有利于载荷标定以及可实现同一目标长期稳定观测.
太阳同步冻结轨道星座的保持主要包括对半长轴、偏心率和轨道倾角的保持.太阳同步轨道为低轨,受大气阻力影响,轨道高度会逐渐降低,偏心率会逐渐减小,不同卫星由于大气阻力和迎风面差异,会引起星座成员之间相位出现相对漂移,影响星座覆盖特性和卫星进出站时序规划,甚至可能出现星座成员相撞的风险.因此必须对每个星座成员的相对相位进行保持控制,也称星座站位保持.然而,冻结轨道对偏心率矢量有要求,所以还需要主动调整和保持各成员卫星的偏心率矢量.太阳同步轨道卫星轨道面与太阳关系相对固定,卫星轨道倾角受太阳光压和太阳引力常值影响,会发生漂移,进而引起升交点赤经漂移速度的改变,最终体现为地方时的漂移.特别是对于有冻结特性或回归特性的太阳同步轨道,更需要轨道倾角保持.
目前针对轨道保持的研究比较多,崔海英等[1-2]给出了低轨卫星轨道轨迹保持方法,以及基于任务的详细参数设计,但是均没有考虑轨道保持中偏心率抑制问题.杜耀柯等[3]将星下点轨迹保持控制问题转化为平均轨道根数相对轨道控制问题,其中目标卫星是虚拟的,优点是每个参数控制精度高,缺点是控制算法复杂,轨控推力为空间指向,燃料消耗大,轨控次数频繁.谢挺等[4]分别通过单脉冲和双脉冲方法,介绍了超低轨道高度保持和偏心率主动圆化控制,属于单星轨道绝对保持,不适用于冻结轨道此类特殊轨道保持.姜宇等[6-8]采用切向和法向控制,分别实现了对虚拟星的面内面外精确编队保持,但采用的切向脉冲为三脉冲,脉冲中有减速分量,控制频次高,非最低燃耗策略.
本文提出一种太阳同步冻结轨道星座最小燃耗保持方法及仿真,仅采用沿切向单脉冲抵消大气阻力,同时选择在相对远地点点火,同时实现对目标轨道高度、轨道相位及偏心率矢量的捕获及保持,即实现对目标冻结轨道的面内保持,控制频次低,且切向单脉冲全部用于抵消大气衰减的加速分量,为最低燃耗.
1 轨道摄动模型
1.1 大气衰减
对于低轨卫星,大气阻力造成轨道机械能的长期衰减[6],大气阻力产生与卫星速度相反的阻力,对应的阻力为

(1)
式中:T为切向阻力大小,单位N;CD为阻力系数,对一般卫星其取值范围为2.0~2.3;S为卫星有效迎风面积,单位m2;ρ为卫星飞行高度处的大气密度,单位kg/m3.
大气阻力将造成轨道面内参数半长轴a(单位m),偏心率e,近地点幅角ω随时间的变化[9],其表达式为

(2)
式中,θ为卫星真近点角,单位rad;E为卫星偏近点角,单位rad;r为地心距,单位m;p=a(1-e2)为轨道半通径,单位m;n为卫星轨道运动平均角速度,单位rad/s.
1.2 太阳引力
对于太阳同步轨道,地球非球形引力引起的轨道面进动[10-11]平均角速度与太阳绕地球的视运动平均角速度相等,太阳始终在轨道面的一侧,同时卫星绕地球沿轨道运动,会产生力矩,导致轨道倾角产生长期变化项,该现象称为太阳引力谐振,轨道倾角i产生单方向漂移[11],其表达式为

(3)
式中,ns为地球绕太阳运动平均角速度,单位rad/s;β为太阳高度角,单位rad.
1.3 轨道面进动
低轨卫星轨道升交点赤经Ω进动速率近似表达式为[10]:
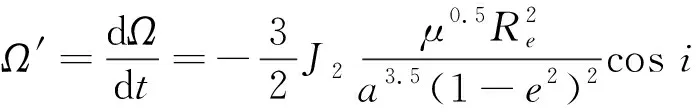
(4)
式中,J2为地球形状因子,是最大的地球带谐项系数;μ为地球引力常数;Re为地球平均半径.
根据式(4),轨道半长轴a的变化和轨道倾角i的变化均会引起升交点赤经速率的变化,并最终导致太阳同步轨道降交点地方时的变化,将Ω′分别对轨道半长轴a和轨道倾角i求导:
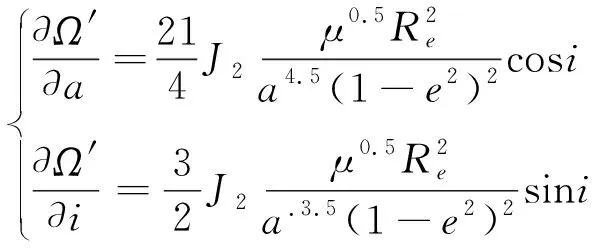
(5)
式(5)分别给出了轨道半长轴a和轨道倾角i变化对升交点赤经漂移率的影响,用于计算太阳同步轨道地方时漂移速率.
2 轨道保持策略
星座保持一般分相对保持和绝对保持,相对保持需要综合考虑其他星座成员卫星轨道信息[12-13],策略复杂;绝对保持策略简单,轨道保持策略不受星座成员数量的影响,工程适用性好.本文研究采用星座绝对保持策略,即给每颗星座成员卫星分配一个虚拟目标星(简称“虚拟星”),每颗星座成员实现了对应的虚拟星跟踪,就实现了星座的绝对保持.
星座同一轨道面内相对轨道相位漂移较快,因此具有控制频次高,单次控制量小的特点,而轨道倾角相对漂移较慢,因此轨道面外保持具有单次控制量大,由于一般控制频次低的特点,面内面外控制不同步,可将星座保持分为面内保持和面外保持解耦控制.
3 面内保持
轨道保持可视为本星相对于虚拟星的轨道绕飞保持控制问题,轨道保持目标是与虚拟星距离趋于0,认为两星足够接近,忽略高阶小量.定义4个面内新轨道要素描述相对运动[14-16]:

(6)
式中,n1为伴随星平均角速度,单位rad/s;n0为虚拟星平均角速度,单位rad/s;δn为两星平均角速度之差,称为相对漂移率,单位rad/s;δe‖,δe⊥为两星指向近地点的偏心率矢量之差在参考星节点坐标系中的投影;δu为两星相对轨道幅角偏差,单位rad.
以虚拟星为原点,虚拟星轨道坐标系为参考坐标系,根据文献[14],或对文献[15-16]进行高阶小量近似,可得伴随卫星面内相对运动方程:

(7)
式中:τ为从初始时刻算起的时间,单位s;u0为虚拟星轨道幅角,单位rad,δe=[δe‖δe⊥]T为相对偏心率矢量.

对伴随星施加脉冲作用下,可认为卫星位置没有变化,据此有轨道面内相对轨道机动方程[14]

(8)
式中:Δvx为轨道系x方向速度增量(切向速度增量),Δvz为轨道系z方向速度增量(径向速度增量).
可以看出,切向速度增量Δvx可以同时对卫星相对漂移δu,相对漂移速率δn,相对偏心率矢量δe进行主动调整;从另外一个角度,切向脉冲可以仅用于克服卫星大气阻力,若能避免使用径向(z)推力,即可实现最小燃耗下的面内轨道保持控制.
令Δvz=0,则式(8)可简化为

(9)
3.1 面内保持时机
传统的一个轨道周期内切向三脉冲面内轨道保持算法,可以在一个轨道周期内实现对虚拟星面内轨道参数的捕获[8],对虚拟星轨道捕获快,但部分速度增量会降低轨道高度,燃料消耗非最优.
本文提出的基于切向单脉冲的面内轨道保持算法,在不约束轨道捕获时间的前提下,采用时间换燃料的思想,选择在面内相对运动远地点附近执行一次切向轨道控制,轨道控制产生的速度增量仅用于抵消大气衰减,利用主动轨控和被动大气衰减效果,同时实现面内所有轨道参数的捕获及保持.


(10)
根据式(10),且Δvx>0,可得最优轨控点U0
U0=π+atan2(δe⊥,δe‖)
(11)
当轨道控制点为U0时,两星相对偏心率矢量的模减小速度最快,及两星相对运动椭圆尺寸减小最快.从轨道物理意义上描述:δe=[δe‖δe⊥]T是相对偏心率矢量,atan2(δe⊥,δe‖)代表基于相对偏心率矢量计算出的相对近地点角(相对近地点与升交点之间的角度),U0即为相对远地点.
反之,若Δvx<0(这里仅用于案例讨论,该假设与本文轨道保持策略不符),则在相对近地点执行轨控,同样可使轨控后两星相对偏心率矢量的模尽量小.
3.2 面内保持稳定性分析
根据式(9),可以看出偏心率矢量增量方向滞后速度增量方向90°[17],针对3.1节面内保持时机为相对轨道的远地点,即偏心率矢量增量方向与当前相对偏心率矢量方向相反,意味着相对偏心率矢量的模减小最快.
在虚拟星轨道面内,建立偏心率矢量坐标系如图1所示.
图1中,δe0为初始相对偏心率矢量,δef为轨控后相对偏心率矢量,Δδe为实际轨控引起的相对偏心率矢量变化量,Δv为实际轨控产生的迹向速度增量,Δδe0为理想轨控引起的相对偏心率矢量变化量,Δv0为理想轨控产生的迹向速度增量.
图1可以看出,Δδe与Δδe0夹角(即Δv与Δv0夹角)越小,轨控后|δef|最小,即在轨控量一定时,在相对远地点进行轨道升高控制,轨控后相对偏心率矢量的模最小.
图1还可以看出,如果一直在最佳轨控点轨控,当|Δδe|<|δe0|,则最佳轨控点一直保持不变,直到|Δδe|≥|δe0|,在最佳轨控点的轨控会使δe0反向,即最佳轨控点会变化180°,并持续如此循环往复.
当|Δδe|≤2|δe0|,只要Δδe和Δδe0夹角小于θ,就有|δef|≤|δe0|,即轨控后相对偏心率矢量的模比轨控前相对偏心率矢量的模小.根据图1几何关系有
(12)
根据式(12),当|Δδe|≼|δe0|时,θ趋近于90°,即当轨道保持引起的相对偏心率矢量变化量的模远小于当前相对偏心率矢量的模时,在相对远地点附近90°范围内沿迹向轨道保持,轨控后相对偏心率矢量的模就会趋于减小.
假设大气阻力不变,每次轨控引起的|Δδe|可视为常值,而|δe0|不断变小.一旦|Δδe|>2|δe0|,|δe0|不再减小,相对偏心率矢量达到稳定状态.因此,跟踪星轨道偏心率稳态误差即单次轨道保持产生相对偏心率矢量变化量的模.
3.3 面内保持控制量
实现跟踪星轨道保持,不仅需要调整两星相对偏心率,还需要调整两星相对轨道幅角.

图2 轨控前后两星相对轨道幅角变化率Fig.2 Relative angular velocity of two satellites’ orbital arguments before and after orbit control

图3 轨控前后两星相对轨道幅角Fig.3 Relative orbital argument of two satellites before and after orbit control

根据上述规划,有如下约束:

(13)

可以计算得,跟踪星相对轨道幅角漂移率控制量为

(14)
卫星半长轴衰减率与两星轨道幅角相对漂移率的关系[18-19]:

(15)
式中,a0为虚拟星轨道半长轴,单位m.
结合式(14)和(15),有

(16)
根据脉冲变轨假设,1s内实现速度增量,结合式(15)和式(16),变轨前后轨道半长轴增加量为

(17)
根据低轨圆轨小量调整时轨道高度变化量Δa与速度增量Δvx之间关系[17-19].
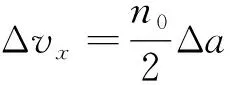
(18)
结合式(17)和式(18),可得切向速度增量为

(19)

考虑到工程约束,仅有沿着飞行方向的速度增量,要求式(19)中Δvx≥0,因此
Δvx=

(20)
轨道幅角保也是轨道周期保持,根据开普勒第三定律,轨道周期保持也是轨道半长轴的保持,即轨道平均高度保持.
4 面外保持
面内保持可实现轨道高度保持,因此在太阳同步轨道地方时保持时,可仅考虑轨道倾角保持.
由于卫星轨道倾角漂移速率较慢,为10-13rad/s量级[11],为简化控制策略,可采用传统阈值触发的方式来实现卫星倾角调整:即当地方时漂移超过阈值T,则择机在附近的升/降交点执行轨道倾角调整,倾角调整量为
Δi=2(i0-i)
(21)
式中,i0为虚拟星轨道倾角,单位rad;i为跟踪星当前轨道倾角,单位rad.
轨道系y轴方向速度增量为(以在降交点控制为例)
Δvy=2(i0-i)n0a0
(22)
实际上,由于倾角漂移慢,轨控频次低,若要提高地方时保持精度,适当提高倾角调整频率即可.
5 仿真与分析
采用绝对保持策略,每颗卫星正常执行轨道保持,即实现星座保持,以其中某颗卫星轨道保持为例仿真说明,仿真条件如下:仿真起始时间(北京时间):2020-06-08 12时,仿真时长为4年.大气阻力引起轨道平均衰减为每年降低10 km;要求降交点地方时保持精度为0.4 min(对应星下点赤经漂移12.6 km,轨道面外控制阈值T取12 km),星座成员与对应虚拟星之间相位保持精度为0.002°(对应飞行方向误差0.252 km,轨道面内控制阈值S取0.1 km).

表1 虚拟星和跟踪星初始轨道参数Tab.1 Initial orbit parameters of the virtual satellite and tracking satellite
图4和图5可以看出,实现了针对虚拟星的逼近及稳定伴飞,即实现了对指定站位的捕获及保持,两星相对距离保持精度约0.2 km,优于指标要求0.252 km.

图4 虚拟星轨道坐标系下X和Z位置Fig.4 X & Z position in orbital coordinate system of the virtual satellite

图5 虚拟星轨道坐标系下X和Z位置放大图Fig.5 Enlarged drawing of X & Z position in orbital coordinate system of the virtual satellite
图6可以看出,实现了升交点赤经保持,升交点赤经相对漂移误差小于指标要求的12.6 km.

图6 升交点赤经相对漂移Fig.6 Relative drift of the RAAN
图7可以看出,初始时刻跟踪星轨道高度比虚拟星低1 km,跟踪星轨道幅角比虚拟星小2°,系统判定无需轨道保持,待两星轨道幅角差大于控制阈值,执行一次脉冲轨道保持,即实现对虚拟星轨道幅角的捕获.

图7 虚拟星轨道坐标系下X-Z位置相平面图Fig.7 Phase plane of X-Z position in orbital coordinate system of the virtual satellite
图8,图9,图10可以看出,实现了虚拟星轨道偏心率矢量的捕获及保持,即实现了冻结轨道保持,轨道偏心率保持精度约5×10-6.

图8 跟踪星轨道偏心率Fig.8 Orbital eccentricity of the tracking satellite

图9 跟踪星轨道偏心率放大图Fig.9 Enlarged drawing of the tracking satellite orbital eccentricity

图10 相对偏心率矢量相平面图Fig.10 Phase plane of relative eccentricity vector
图11可以看出,实现了虚拟星轨道半长轴捕获及保持.图12可以看出,实现了太阳高度角(星下点地方时)的保持.

图11 跟踪星轨道半长轴Fig.11 Orbital semi-major axis of the tracking satellite

图12 跟踪星太阳高度角Fig.12 Beta angle of the tracking satellite
图13给出了轨道保持所需速度增量的变化过程.

图13 跟踪星燃料消耗历程Fig.13 Fule consumption history of the tracking satellite
本仿真中,跟踪星轨道动力学模型考虑了大气衰减,J2摄动,太阳引力摄动,采用的解析法轨道递推,基于脉冲变轨假设模型,因此本文计算燃料消耗可供定性参考;本仿真所有轨道参数描述均为平根;本仿真未考虑轨道确定误差.
6 结 论
1)轨控时机选在轨道远地点执行轨控,可实现对目标轨道偏心率矢量的捕获和保持.相对运动椭圆大小,与大气衰减速度有关,衰减速度越快,则执行切向控制的速度增量相应越大,偏心率矢量改变量越大,相对运动椭圆收敛越快(即与目标轨道重合度越好).
2)保持精度主要与定轨精度、最小速度脉宽和轨道演变速度有关.定轨精度越高,最小速度脉宽越小,轨道演变速度越慢,则轨道保持精度越高.
3)采用切向单脉冲的轨道保持策略,所有速度增量均沿卫星飞行方向,完全用于抵消大气阻力引起的轨道高度衰减,因此属于最小燃耗轨道保持.
4)通过控制本星与虚拟星的轨道偏差,可使星座成员均保持在各自轨位附近,最终实现整个星座的保持.如果把虚拟星从星座替换为低轨卫星编队或集群,且虚拟星半长轴不衰减或衰减速度慢于所有编队成员真实衰减速度,本文面内轨道保持技术也适用.
