基于奇异摄动法的水下机器人串-并联PID控制

王鸿儒， 刘云平, 马金虎， 严 乐

南京信息工程大学自动化学院, 南京 210044

0 引 言

PID控制的发展历史悠久，算法简单且易于实现，拥有较高的鲁棒性和可靠性[1].经典PID控制适用于单输入/单输出的线性系统，在处理水下机器人系统受到的外界干扰时，性能受到限制.因此，众多改进的PID控制算法正广泛应用于水下机器人控制系统中.

尹卿卿等[2]提出了一种基于扩展状态观测器的模糊PID控制策略，扩展状态观测器补偿UAV系统干扰，实现了水下机器人的航向和俯仰控制.HARUN等[3]采用粒子群优化算法对PID反步控制器参数增益进行优化，提高了水下机器人的应用性能.

杜度[4]为解决水下机器人在短时间内到达指定深度问题，提出了一种基于RBF神经网络的参数自整定PID控制方法，使得PID各参数能够完成自整定.万俊河等[5]为提高水下机器人的运动性能，提出了一种分数阶PID控制策略，可以有效地找到PID控制器的最优参数.马艳彤等[6]使用过渡目标过程调节误差反馈，优化水下机器人控制过程的动态响应.KHODAYARI[7]针对水下机器人设计了一种基于非线性模型的自适应模糊PID控制器，提高了机器人的稳定性和动态性能.

目前，针对串级PID控制的优化主要集中于参数整定方面，对串级PID控制结构优化的研究较少，在应用于例如水下机器人的非线性系统时，不能保证系统的稳定性[8].另外，水下机器人系统的不同状态间存在较高的耦合性[9]，给水下机器人的位置姿态控制与速度控制研究增加了难度，导致水下机器人系统在遭遇外界强干扰时，严重偏离期望状态[10].奇异摄动法和快慢分解法是处理快慢动态耦合复杂系统的强有力工具，其思想是在两个时间尺度内分别完成设计控制器的任务，最后用降阶系统近似替代原系统的动力学行为进行控制器设计[11-12].

本文针对串级PID控制应用于水下机器人位置、姿态控制时出现的收敛速度慢、抗扰动能力差等问题，基于奇异摄动方法、串级控制方法和非线性整定方法设计串-并联PID控制(SPPID)，使用计算流体动力学与最小二乘法测定水动力参数.仿真与实验结果表明，该方法能够增强水下机器人系统的鲁棒性，降低收敛时间，缩小系统遭遇强干扰时的控制误差.

1 串-并联PID控制

水下机器人的动力、运动学模型可简化为

(1)

式中，v为速度角速度向量，η为位置姿态向量，M为惯量矩阵，C(v)为科氏力与向心力矩阵，D(v)为粘性水动力矩阵，f2为重浮力和力矩，f3为扰动力和力矩，f4为推进器输入的控制力和力矩，Q为转换矩阵.

式(1)所示的水下机器人模型为二阶系统，且位置姿态向量η与速度角速度向量v之间存在耦合关系，给小型水下机器人的位置姿态与速度控制研究增加了难度，使用奇异摄动方法可解决模型的耦合问题.在奇异摄动控制领域，时标分解法是较为重要的方法.时标分解法的基础假设认为，一个整体的系统可以分解为快变化(非主导因素)和慢变化(主导因素)两个子系统[13].在快子系统变量变化时，慢子系统变量几乎保持不变；当慢子系统的变化已无法忽视时，快子系统变量则已经稳定，也就是说快子系统变量会比慢子系统变量更早地进入稳态.

图1为在Simulink中运行的水下机器人模型进行全速浮潜运动时的速度输出，模拟得出小型水下机器人的理论下潜最大速度约为1.3 m/s.从图1可以看出，速度、角速度变量的变化是直接的阶跃，在短时间内快速变化并达到稳态，而位置、姿态变量的变化速度较慢，因此，速度、角速度可作为快变量，位置、姿态可作为慢变量.

图1 机器人进行浮潜时的速度输出Fig.1 Output of the snorkeling robot

在上述论断的基础上，将式(1)所示的小型水下机器人数学模型变为奇异摄动模型.注意到，式(1)中的矩阵M为非零对角方阵，故M为可逆阵.且f3一般是由较大的元素组成的向量，这里引入一个较大的常数c，使得

f3=cfc

于是式(1)可变为

(2)

式中，ε=c-1为奇异摄动参数，u(t)=f4为控制器输入，M3=c-1M-1，x2(t)=η为位置姿态向量，x1(t)=v为速度角速度向量.式(2)便是本文推导出的小型水下机器人的奇异摄动模型，下面使用时标分解法对模型进行快慢分解.

奇异摄动方法能够根据不同时间尺度，将原本的耦合系统解耦，分解为快子系统和慢子系统，从而得出原系统的两个近似解——快变量和慢变量[14-15].根据两个近似解，可以分别进行控制律设计达到预期的控制目标.设快变量的快子系统控制律为uf(t)，慢变量的慢子系统控制律为us(t)，则针对两个变量的整体控制律为[16-17]

u(t)=us(t)+uf(t)

(3)

当ε→0时，t在时间尺度下，设慢系统输入为us(t)，于是式(2)有唯一根

x1s(t)=(C(v)+D(v))-1(us(t)+f3-f2)

(4)

对于快子系统，由式(2)～(4)可得

x1(t))+M3uf(t)

(5)

(6)

针对式(4)所示的慢子系统模型，设计PID控制量us(t)为

(7)

式中，KPs、KIs、KDs分别为慢子系统比例、积分、微分系数，es(t)为慢子系统期望与输出误差，uDs(t)为慢子系统期望.

针对式(7)所示的快子系统模型，设计PI控制量uf(t)为：

(8)

式中，Kpf、KDf分别为快子系统比例、微分系数，ef(t)为快子系统期望与输出误差，uDf(t)为快子系统期望.由式(2)、(4)、(7)、(8)可得基于奇异摄动模型的优化并联PID控制量u1(t)为

(9)

目前，针对多旋翼无人机的串级PID控制理论发展已十分完善.串级PID控制器由两个串接在一起的PID控制器组成，能够有效减少控制回路中的二次扰动，具有更多可调节的PID参数，使得控制效果与系统鲁棒性大幅度提高，显著缩短系统的响应时间.采用串级PID控制器，将并联PID控制器作为外环，内环PID控制器根据外环输入解算出控制量，控制流程如图2所示，可得串-并联PID控制器控制量u2(t)为

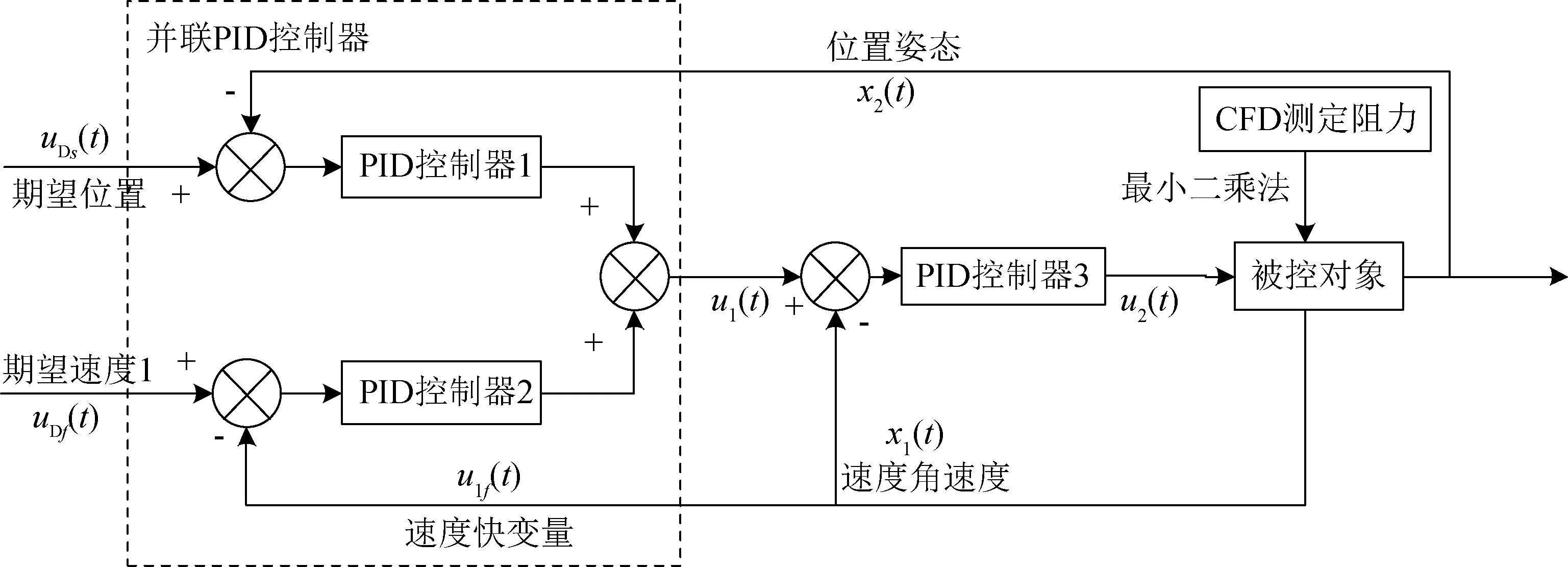
图2 串并联PID控制流程Fig.2 Series-parallel PID control process

(10)

2 水动力参数测定

本文仿真与实验以自主开发的小型水下机器人为基础进行，如图3所示，需测定其水动力参数.

图3 小型水下机器人Fig.3 Small underwater vehicle

水动力参数是一组未测定的常量，其数值影响着粘滞阻力与惯性阻力的变化，进而影响着水下机器人各状态量的稳定性.水动力参数测定与水下机器人的几何外形密切相关，由于本文采用开架式结构，速度较小，在水动力参数测定时可忽略各自由度运动耦合造成的影响.根据文献中各矩阵的具体形式，本节需要测定的水动力参数有：

(1) 速度参数：FxVx，FyVy，FzVz，FxVx|Vx|，FyVy|Vy|，FzVz|Vz|.

(3) 角速度参数：Mxp，Myq，Mzr，Myq|q|，Mzr|r|.

由于水下机器人六自由度的水动力参数测定过程类似，本节以横荡运动为算例阐述计算过程.首先，使用计算流体动力学(CFD)仿真法测定不同工况下的阻力和力矩.在FLUENT图形编辑器中导入Solidworks绘制的水下机器人简化模型，绘制计算域并划分网格，使用标准k-ε模型，通过使用SIMPLE算法计算，设置迭代次数为400，并设置边界条件.将流体流速设置为0.1～0.8 m/s，迭代过程如图4所示.

图4 迭代过程Fig.4 Iterative process

经过400次的迭代计算，各项指标残差均已收敛，将水下机器人水动力保留到二阶的辨识方程[18]，通过最小二乘法[19]，利用FLUENT求解出水流匀速运动和加速度为0.1 m/s时机器人所受横荡运动阻力，分别拟合出粘性阻力、附加质量系数，通过以上受力测定，最终拟合出水下机器人的水动力参数见表1.

表1 水动力参数表Tab.1 Hydrodynamic parameters table

3 仿真与实验

3.1 算法仿真

本次仿真使用Matlab/Simulink联合模拟，根据表3中所测定的水动力参数，使用Matlab编写小型水下机器人数学模型和串-并联PID控制器，并将其链接到Simulink中的S-function中，所搭建的仿真模型见图5.

图5 仿真框图Fig.5 Simulation block diagram

设机器人重力与浮力相等，且使用Solidworks中质量参数功能可以获得模型中未知参数取值为

m=13.76 kg，Ix=3.35，Iy=3.19，Iz=4.68

由于小型水下机器人主要的控制需求是姿态控制和深度控制，故本次仿真从与之相关的4个自由度运动考察控制效果.根据文献[19]，选择3个关于误差e(t)的非线性函数作为PID参数的自适应函数.对于比例系数Kp，自适应函数为

Kp(e(t))=ap+bp[1-sech(cpe(t))]

(11)

其中，ap、bp、cp为约束常数，ap、bp约束取值范围，cp约束变化速度.对于积分系数KI，自适应函数为：

KI(e(t))=aIsech(cIe(t))

(12)

其中，aI、cI是约束常数，aI限制KI的取值，cI约束KI的变化速度.对于微分系数KD，自适应函数为：

(13)

其中aD、bD、cD、dD为约束常数，aD、bD、cD共同约束KD的取值范围，dD约束KD的变化速度.式(12)～ (13)的自适应函数的变化趋势如图6所示.

图6 参数变化趋势Fig.6 Trend of parameter variation

首先，对水下机器人浮潜运动进行仿真，对比经典PID控制与优化并联PID控制的控制效果，结果如图7所示.

图7 两种控制器的实际控制效果Fig.7 Actual control effects of the two controllers

仿真过程中，经典PID控制环节的PID参数相同，期望深度设置为30 m，并联环节期望为0.通过对比控制效果可以得出结论，基于奇异摄动方法设计的并联PID控制能够有效减少经典PID控制因饱和区问题引起的超调，降幅达到56%，且并联PID控制能够加速控制量的收敛，使控制量输出更为平滑，从而避免机器人长时间停留在饱和区而引起控制误差.

接着，使用串-并联PID控制器控制小型水下机器人进行不受干扰的浮潜运动，取Kp为20，KI为3，KD为2，期望深度为20 m，仿真时间为100 s.再将非线性自适应方法加入串-并PID控制器，通过大量的水下机器人实验操作与性能考察，确定相应自适应函数的参数为ap=5，bp=15，cp=1，aI=2，cI=30，aD=0.5，bD=2.5，cD=6.5，dD=0.4，仿真结果如图8所示.

图8(a)表明，通过非线性自适应方法设置PID参数，会略微降低PID控制器的响应速度，随之而来的是超调的大幅度减少和调节时间的缩短，控制效果提高.而从图8(b)可以观察比例、积分、微分系数的变化，非线性自适应方法会根据当前误差值给出适合的参数.

图8 PID控制器自适应效果比较Fig.8 Comparison of adaptive effect of PID controller

考虑外界扰动的影响，在仿真开始时刻，加入大小为的扰动力，模拟渐强的周期性海流对机器人的影响，可以得到如图9所示的控制效果.

图9表明，在加上时变扰动项后，经典自适应PID控制的深度输出会出现明显的振荡现象.在75 s时刻，振荡幅度已高达4 m，控制误差达到20%，动态性能较差.使用串-并联PID控制器可以增强小型水下机器人的动态控制性能，仿真结果见图10.

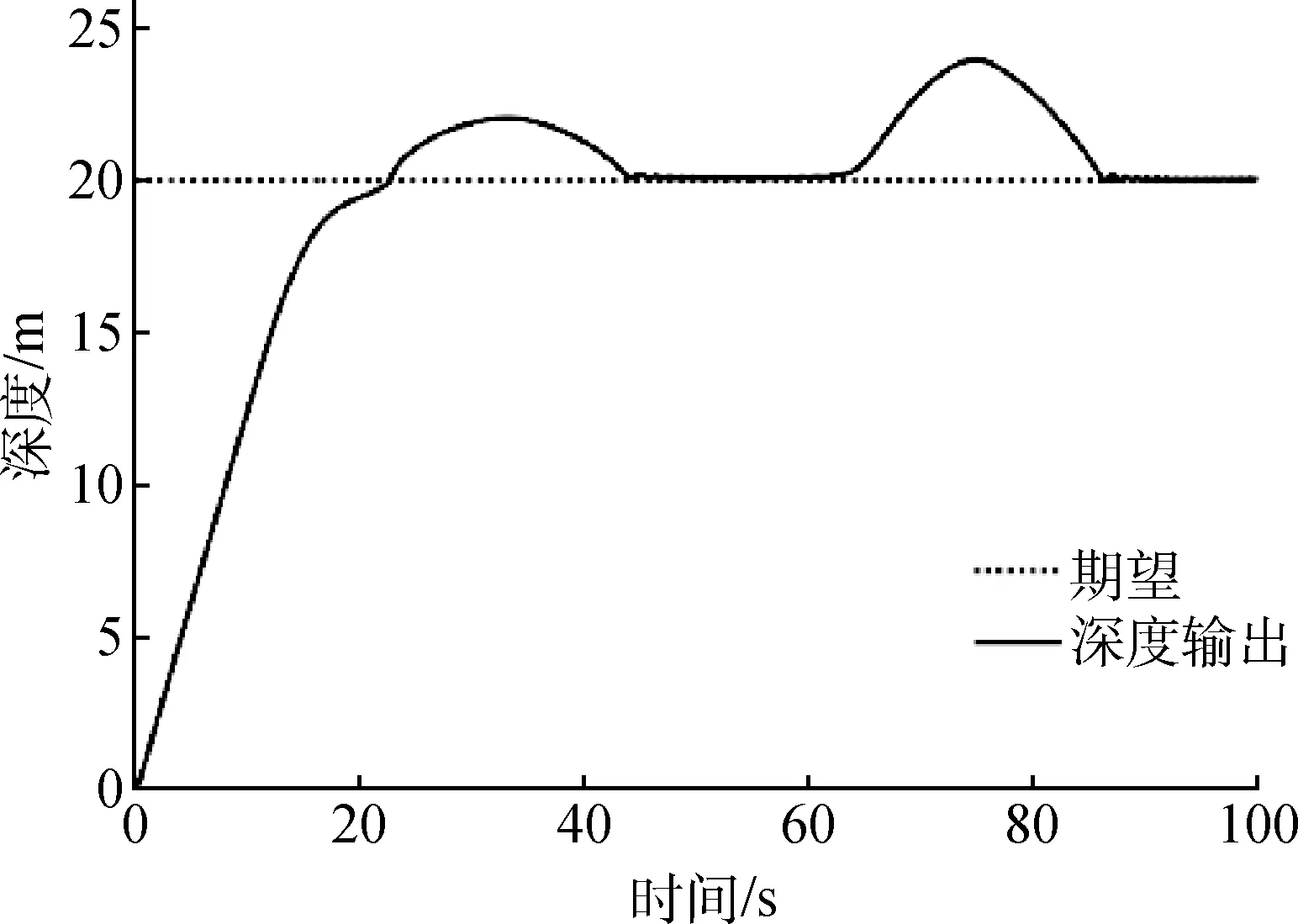
图9 海流干扰下的经典自适应PID控制器效果Fig.9 Effect of classical adaptive PID controller under ocean current disturbance

图10 串-并联PID控制仿真结果Fig.10 Simulation results of series-parallel PID control

从如图10(a)的仿真结果看，即便外界有强扰动，串-并联PID控制仍能够保证深度输出稳定在期望值附近，在较长时间内仅有轻微振荡，振荡幅度为0.7 m，控制误差降低82.5%，动态控制效果较好，控制更为精确.另外，图10(b)表明，串-并联PID控制器能够较好地跟踪外界干扰力，并输出与之相反的控制量，从而抵抗外界扰动.

在进行姿态保持控制仿真时，模拟三轴突然遭遇由70 N·m逐渐变小的强力矩干扰，对比串-并联PID控制器、非线性自适应串级PID控制器与非线性自适应经典PID控制器控制效果，见图11.

图11(a)为非线性自适应经典PID控制器的姿态保持效果，当小型水下机器人的三轴出现干扰力矩时，经典PID控制下的姿态角会出现剧烈的抖动，平均振幅高达±0.4 rad(约22.92°)，且在较长的时间内无法收敛，无法保证控制精度，控制效果较差.

图11 姿态保持效果对比Fig.11 Comparison of attitude keeping effects

使用非线性自适应串级PID控制保持姿态，效果如图11(b)，非线性自适应串级PID控制可使姿态角的最大振幅缩小至0.3 rad，较经典PID控制下降80%.非线性自适应串级PID控制对横滚角、俯仰角有较好的控制效果，能够在短时间内将其收敛至期望值附近，但是对偏航角的控制效果不理想，偏航角的调节时间更长且在75 s后开始发散.

图11(c)为串-并联PID控制器的姿态保持效果，串-并联PID控制能进一步将姿态角的最大振幅缩小至0.15 rad，较非线性自适应串级PID控制下降50%.串-并联PID控制对三轴姿态角均有较好的控制效果，能在短时间内将姿态角误差缩小至0.025 rad(约1.43°).并联环节的加入会加速姿态角的收敛，消除振荡，使得调节时间缩短，控制曲线更为平滑.

综上所述，本次仿真说明，本文所设计的串-并联PID控制器可以有效抵抗外界扰动，控制效果对比非线性自适应经典与串级PID控制均有较大提升，具有更快的收敛速度与更好的鲁棒性，可以实现长时间准确的定深控制和姿态控制.

3.2 抗扰动实验

本文采用如图12所示的造浪泵，1 m内可产生约80 N的干扰力，模拟水流对小型水下机器人的扰动，且机器人的相关参数均有相应进程实时辨识.

图12 造浪泵Fig.12 Wave pump

抗扰动测试的实验步骤是：

(1) 根据所需的水流冲击方向，调整造浪泵的位置；

(2) 切换定深或定航模式，将水下机器人控制器分别设置为非线性自适应经典PID控制与串-并联PID控制，对比控制效果；

(3) 重复上述步骤.

本次实验中，为降低控制板负载，串-并联PID控制器的外环并联环节采用P控制，内环则采用PID控制，首先进行定航模式实验，此模式的功能是保持水下机器人的航向，实验结果见图13.

图13 定航模式实验结果Fig.13 Experimental results of fixed course mode

图13(a)所示，是串-并联PID控制下，小型水下机器人的姿态角输出.水下机器人将三轴姿态保持在0°，2.75 s、10.7 s和18 s时刻，机器人分别遭遇来自顶部、底部和前方的强水流冲击.在三轴姿态改变时，串-并联控制器的响应时间仅为0.3 s，响应速度较快.在2 s内，控制器能将三轴姿态收敛至期望值，姿态的调节速度快.三轴姿态的稳态误差不超过±2.5°，控制精度较高，符合设计指标.

如图13(b)所示，是经典PID控制下，小型水下机器人的姿态角输出.在2.5 s、14.5 s和22 s时刻，机器人分别遭遇图13(a)中相同水流的冲击.与串-并联PID控制对比，经典PID拥有相同的响应速度，但在调节过程中，姿态角的“抖动”剧烈，使得调节时间更长，需要5～8 s才能使姿态角逐步收敛.经典PID控制的稳态误差超过±5°，控制精度相对较低.

综上所述，串-并联PID控制器的姿态控制效果对比经典PID控制器有较大提升，响应时间为0.3 s，调节时间缩短69.23%，稳态误差降低50%.串-并联PID控制器的控制曲线更为平滑，更适用于硬件，能够避免电机、电调等电路因剧烈“抖动”引起的过载而损坏，使得小型水下机器人拥有较好的抗扰动能力.

接着，进行定深模式实验.定深模式的功能是以定航模式为基础，实现当前深度的保持，定深模式下的实验结果见图14.

图14 定深模式实验结果Fig.14 Experimental results of depth determination mode

将机器人深度设置为0.3 m，如图14(a)和14(b)所示，是串-并联PID控制和经典PID控制下，水下机器人的深度输出.在6 s时刻，机器人遭遇来自顶部的强水流冲击.经典PID控制的响应速度较快，但调节时间过长，需要4 s才能使深度输出逐步收敛，且收敛过程会出现明显的振荡.而串-并联PID控制能在2 s内将深度收敛至原值，稳态误差不超过±1 cm，调节时间较经典PID缩短50%，控制效果和精度均有较大提升.两次实验结果均说明，串-并联PID控制对比经典PID控制，控制效果明显提高.

4 结 论

本文针对经典PID控制应用于水下机器人位置、姿态控制时出现的收敛速度慢、抗扰动能力差等问题，提出一种基于奇异摄动法优化串级PID控制策略，设计了水下机器人的串-并联PID控制方法.通过仿真与抗扰动实验对比位置、姿态控制效果，实验结果表明，串-并联PID控制方法具有更快的收敛速度与更好的鲁棒性，抗扰动能力有较大的提升.