永磁同步电机转速滑模和电流预测组合式控制器运行性能分析

邓入川， 赵 迪， 张 山， 苟 浩， 符健豪， 郑 亮， 费 凌*

1. 西华大学机械工程学院, 成都 610039 2. 四川坤成润科技有限公司, 成都 610100

0 引 言

永磁同步电机(PMSM)因其具有可靠性高和功率密度高等优点，常被用于工控交流伺服系统等领域[1]，近些年开始应用于轨道交通运输.由于永磁体作为永磁同步电机转子的重要组成部分，铜耗较感应电机一定程度有所减小，控制精度基本相当，使得国内外专家、学者争相对其展开研究[2-3].虽然永磁同步电机优势突出，但多变量、非线性和强耦合等特性给控制系统设计带来不便[4].目前，矢量控制在永磁同步电机调速系统应用最为广泛.矢量控制通常采用双闭环结构，通过PI对转速环和电流环进行线性调节.但经典PI控制器参数整定过于繁琐，且对电机参数变化的容忍度有限，如果电机因受到干扰内部参数超过适应范围，将导致系统控制精度下降，响应甚至出现大超调[5].随着科学技术的发展，矢量控制的具体实现方式已经得到了改进.

文献[6-7]采用滑模控制(SMC)代替PI来调节转速误差，明显降低了转速超调且提高了电磁转矩响应速度，使得永磁同步电机对负载扰动表现出更强的鲁棒性.为了优化永磁同步电机伺服系统控制性能，文献[8]在速度环中引入模型预测控制(MPC)方法，采用目标函数结果最优的输出作为电流环的输入.实验结果表明，PMSM调速系统的动态性能和静态性能都得到了明显的改善.文献[9]将电流预测控制(CPC)应用于电流闭环，针对传统电流预测控制使用枚举法选择最优电压矢量存在计算复杂的问题，对扇区进行重新划分，简化电压矢量选择的计算，降低电流计算和比较的次数.结果表明，该方法获得了良好的控制效果，稳态时减小了转速抖动，但响应速度未得到明显改善.文献[10]在矢量控制框架下开发了一种模糊自适应内模控制方案，可通过模糊推理识别出惯量并自动调整速度控制器的参数，通过实验证明了该方法的有效性；针对电动汽车控制系统抗干扰能力差的问题，文献[11]采用模糊控制对PI参数进行自适应调整.仿真结果表明，该方法能够有效地增强系统的抗扰动能力，并使得系统对模型参数变化不敏感.

本文在文献[9]电流预测控制(CPC)的基础上，将滑模控制(SMC)用在PMSM矢量控制系统的转速环上，使得电流环获得一个比较理想的参考电流输入.通过建模，并与文献[9]的方案和速度环使用SMC电流环采用PI调节器的控制方案进行仿真对比.结果表明，本文提出的滑模控制和电流预测控制相结合的控制方案能获得更好的稳定性和抗扰动性能.

1 滑模变结构控制

1.1 PMSM数学模型

为了便于分析和设计，忽略磁路饱和等因素，表贴式PMSM的同步旋转坐标系d-q下的数学模型电压方程可表示为[12]

(1)

式中：ud、uq分别为同步旋转坐标系的定子电压d、q轴分量；R为定子电阻；id、iq分别为定子电流d、q轴分量；ψd、ψq分别为d、q轴的定子磁链；ωe为电角速度.

磁链方程为

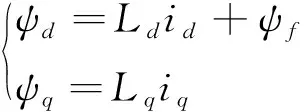
(2)

式中：Ld、Lq分别为d、q轴定子电感；ψf为转子磁链.

电机的机械运动方程为

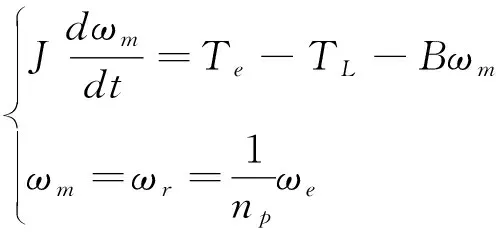
(3)

式中：J为电机转动惯量；ωm为电机的机械角速度；Te、TL分别为电机的电磁转矩、施加的负载转矩；B为阻尼系数；np为电机的磁极对数.

电磁转矩方程则可写为

(4)

对于隐极式三相PMSM，定子电感满足Ld=Lq=Ls，且采用id=0的控制策略.则电磁转矩方程可简化为

(5)

1.2 改进滑模控制器

一定程度上，PMSM矢量控制系统的转速环调节器的性能优劣间接决定了电流闭环调节的品质.为了改善系统的动态性能，本文采用滑模变结构控制方法来代替传统的PI对速度环进行调节.

为了方便调速控制器的设计，将式(2)代入式(1),则PMSM在d-q坐标系下的模型可写为

(6)

式中，Ls为定子电感.

忽略阻尼系数对滑模控制器的影响，将式(5)代入式(3)可将机械方程写为

(7)

对于隐极式PMSM而言，采用id=0的转子磁场定向控制方法可获得较好的控制效果，则可将数学模型式(6)和式(7)重写为[13]

(8)

定义PMSM调速系统的状态变量

(9)

在工程中机械时间常数远大于电磁时间常数，可认为转速及其给定值、负载力矩在控制周期前后大小无变化.根据式(8)和式(9)可得

(10)

(11)

考虑到单滑模面在速度误差调节过程中在固定斜率作用下会造成系统短暂失衡和响应超调，可在系统即将达到平衡时降低滑模面斜率，从而避免了速度响应出现明显抖振，可定义变滑模面函数为

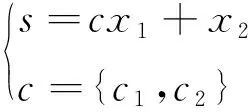
(12)

式中，集合{c1,c2}中的元素满足：c1,c2>0.

系统在稳定前需要具有较好的动态品质，而在系统平衡阶段被看重的是稳态性能.因此在响应前期的正常运动阶段采用指数趋近律，而在后期则采用趋近速率较慢的等速趋近律.即

(13)

式中：ε1，ε2，q为设计参数，且要求数值大于零；λ为趋近律切换系数，其大小决定了系统的速度响应的上升时间，同时也影响着系统稳定性.

另外，由于上述趋近律中不包含状态变量X，因此状态变量x2中的微分扰动对趋近律不会产生干扰.式(12)求导可得

(14)

进一步由式(13)和式(14)可得

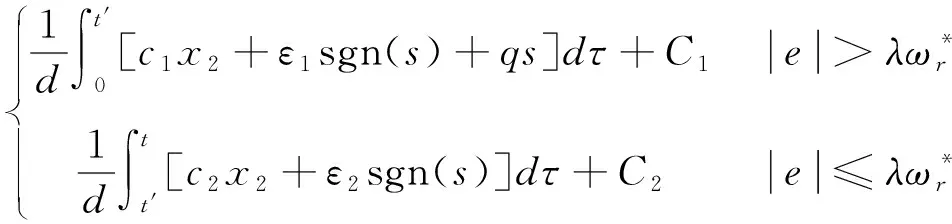
(15)

式中：t′为系统达到临界条件的时间;常数项C1和C2的大小可通过系统初始条件和临界条件确定.

由式(15)可以看出，当远离滑模面时，以变速和指数趋近律向滑模面运动；当接近滑模面时，系统达到切换条件，以新的变速趋近律靠近滑模面，穿越滑模面的速率仅与转子角速度变化率有关.因此误差会越来越小，在理想状况下响应将沿着滑模面稳定于原点.

(16)

由上述趋近律(13)，显然满足上述稳定条件，可知在ε1>0,ε2>0,q>0 情况下系统是渐近稳定的.引入稳定判据

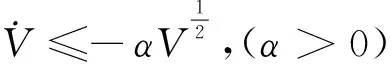
(17)

式中，α为待定判定系数.对式(17)进行积分，积分时间为t

(18)

根据式(18)可知，V将在有限时间tr内达到稳定，且α越大，达到稳定的时间越短，即

(19)

根据以上对稳定判据的分析，针对判定条件的改变，控制器调整为

(20)

经过上述推理，本文设计的滑模转速调节器控制结构简图如图1所示.为了保证系统的稳定性，要求λ∈(0,0.3)，设趋近律切换系数λ=0.1.

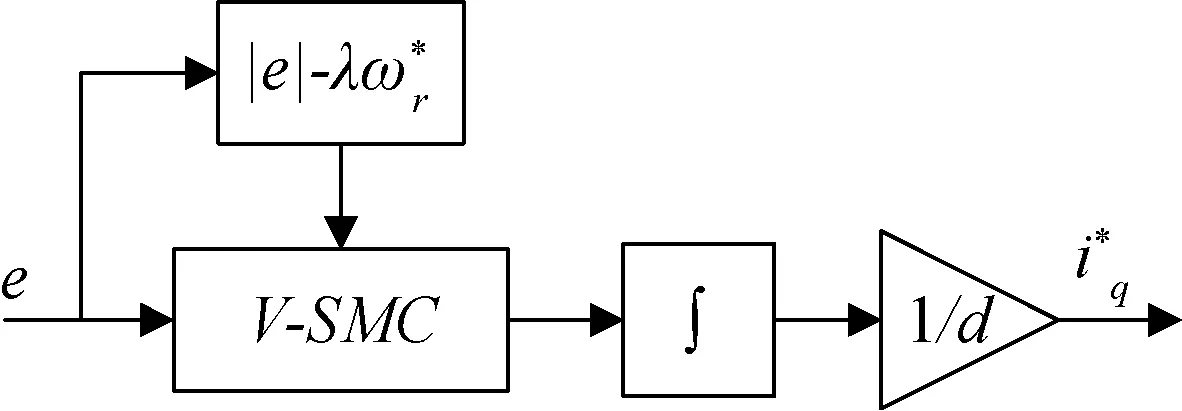
图1 滑模控制器框图Fig.1 Block diagram of sliding mode controller

2 电流预测控制

为了补偿数字控制系统采样周期时延，改善电磁转矩响应的动态品质，在上一小节的控制得到精准的q轴参考电流的基础上，在电流环中采用电流预测控制(CPC)方式来保证定子电流的品质.

在永磁电机的同步旋转坐标系下，对其做符合工程应用的假设，重写隐极式PMSM的参考模型[9]

(21)

式中I为二阶单位矩阵.

在离散模型下，控制周期内转子位置变化很小，为了便于预测，将电角速度ωe视为常数.将式(21)离散化，得到离散后的电流预测模型

(22)

三相交流PMSM的逆变器驱动模块可简化为图2，由此可根据图中三组开关的状态把电机空间电压矢量简化为6个非零基本电压矢量：U1(100)、U2(110)、U3(010)、U4(011)、U5(001)、U6(101)；1个零矢量：U7(000或111).

图2 三相PMSM逆变器驱动简图Fig.2 Diagram of three-phase PMSM inverter drive

空间中的各电压矢量组合如表1所示.

表1 空间基本电压矢量表Tab.1 Table of space basic voltage vector

将上表的7种基本空间电压矢量映射至复平面中，即可得到空间电压矢量分布图.6个非零基本电压矢量将复平面分为6个扇区，如图3所示.

图3 空间基本电压矢量分布Fig.3 Space distribution of basic voltage vector

当前采样周期的ud、uq通过uA、uB、uC等功率Clark变换和Park变换得到，即

(23)

式中：

为了避免传统电流预测在一个控制周期内计算、比较次数过多的情况，首先对零电压矢量作用时的参考电流与其预测值两者的误差进行预测，即

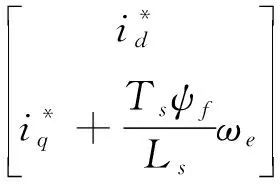
(24)

通过设置误差阈值的方式来确定电压矢量的选择范畴，即|ed0|≤edmin，|eq0|≤eqmin时以零电压矢量为最优，否则最优矢量从6个非零电压矢量中选取.由式(22)和式(24)可得，参考电流与电流预测值之间的误差为

(25)

电流预测控制的最终目标是使得电流误差达到最小，考虑到在理想情况下误差为零，由此可得到理想电压矢量与d轴的夹角

(26)

根据上述空间位置，由式(27)即可求得理想电压矢量

(27)

式中：|Vs|为电压矢量幅值；θ为d轴与α轴的夹角；“”为取余运算.

从而根据图3就近选取有效矢量.

3 仿真实验

为了验证基于趋近律可变滑模调节器的合理性，在电流闭环中采用电流模型预测的基础上，速度环引入本文的SMC算法.在Matlab/Simulink平台上搭建模型，并与文献[9]中的控制方法进行仿真对比.电机内部参数设置见表2.

表2 PMSM仿真预设参数表Tab.2 Preset parameter table of PMSM simulation

本文提出的改进矢量控制系统框图如图4所示，仿真共分为三项：1)空载下改变给定转速，考察PMSM的转速响应的动态性能和稳态性能；2)固定转速，改变负载转矩，考察电机的转矩特性，并分析定子电流；3)转速和负载均不变，考察定子电阻漂移对系统的影响.

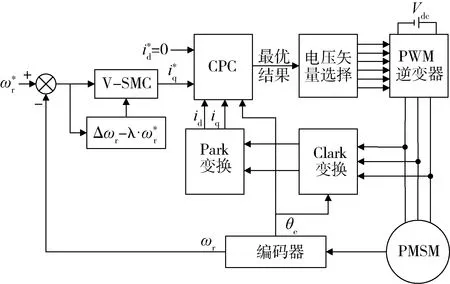
图4 PMSM改进矢量控制框图Fig.4 Block diagram of PMSM improved vector control

为验证提出的方法的有效性，还搭建了电流环PI控制结合转速环滑模算法的PMSM矢量控制模型,与上述两种方法进行比较.

初始永磁体磁链与三相交流的A轴重合，逆变器直流端电压Vdc=510 V，仿真时长为0.7 s，采样周期为T=50 μs.滑模控制器参数设置为：滑模面待设计参数c1=312、c2=190；为便于参数整定，趋近律参数设为ε1=ε2=216、q=1.05.转速环PI调节器参数：Kp1=6、Ki1=120；电流环PI调节器参数：Kp2=30、Ki2=200.

1) 电机空载，初始给定转速10 rad/s，在0.3 s时斜坡上升至15 rad/s，记录转速和q轴电流响应.

根据图5和图6可知，速度环引入SMC控制器能够提高系统转速响应的动态性能，从启动到稳定所用时间减小60%，且其稳态性能也有所改善.

图5 空载实验的速度响应曲线Fig.5 Speed response curve of no-load experiment

图6 空载实验转速误差响应曲线Fig.6 Speed error response curve of no-load experiment

由图7可以看出，永磁同步电机空载运行，3种方案的q轴电流在转速变化时经过调节后回到稳定状态iq=0.本文速度环控制方法的引入使得q轴电流的对转速变化的响应速度有所改善.

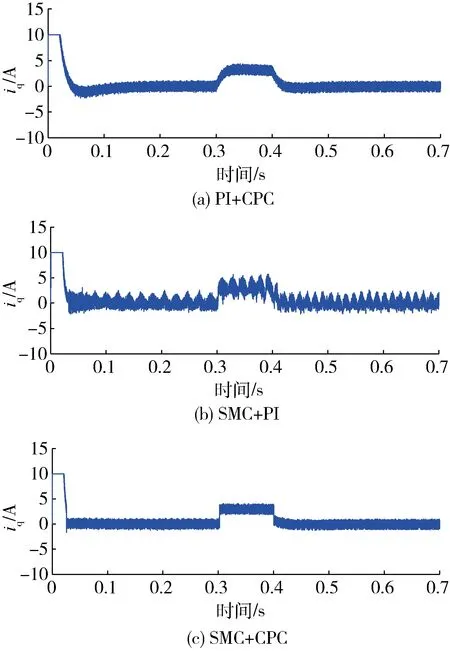
图7 空载实验的q轴电流曲线Fig.7 q-axis current curve under no-load experiment

2)给定电机转速保持在8 rad/s，给定负载转矩为50 N·m，在0.3 s时上升至100 N·m，并记录下转速、转矩和三相电流的响应情况.

由图8可知，系统从开始到稳定和对转矩扰动调节的过程中，与转速环PI调节器相比，基于SMC控制器的系统速度响应无超调，CPC预测算法较电流环PI调节减小了速度响应的抖振.

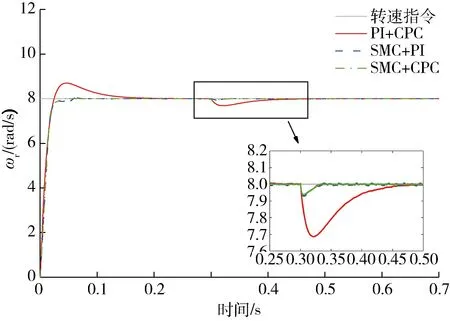
图8 变负载实验的速度响应曲线Fig.8 Speed response curve under variable load experiment

由图9可知，3种方法都能较好地跟踪负载力矩，而滑模引入改善了转矩响应速度，CPC则增强了转矩稳定性.本文巧妙结合了两者的优点.

图9 变负载实验的电磁转矩响应曲线Fig.9 Electromagnetic torque response curve of variable load experiment

通过3种方案的仿真实验结果对比，记录下电机三相定子电流的变化情况，图10为表贴式PMSM的三相定子电流变化波形图.

图10 变负载实验的三相定子电流波形Fig.10 Three-phase stator current waveform of variable load experiment

从图10可看出，3种方案的三相定子电流的正弦度均得到保证，CPC抑制了三相定子电流杂波，从而证实本文SMC结合电流预测的方法是有效的.

为了进一步验证本文提出方法的优越性，单独对上述三种控制方案在电机达到稳态后的A相定子电流作FFT分析，频谱分析结果如图11所示.

图11 定子A相电流频谱图Fig.11 Spectrum diagram of A phase stator current

从图11可以看出，(a)方案的A相定子电流的谐波失真THD=7.01%，(b)方案的A相定子电流的THD=5.44%，(c)方案的A相定子电流的THD=3.60%.由于SMC对转速误差调节较PI控制更精确，使得精准的q轴参考电流经过CPC控制器预测后，输出的PWM波得到改善，逆变器开关频率更稳定，从而降低了定子电流的谐波含量.

3)给定转速8 rad/s，负载转矩50 N·m，0.5 s前定子电阻恒定，0.5 s后引入定子电阻漂移干扰,漂移幅度为±30%，变化范围为(3.65±1.1) Ω，考察转速和转矩响应.

从图12可看出，方案(b)在引入电阻漂移干扰后出现系统失衡，转速出现大的抖振；引入干扰后方案(a)和方案(c)的转速均能稳定到转速指令，且方案(c)的稳定性更好.

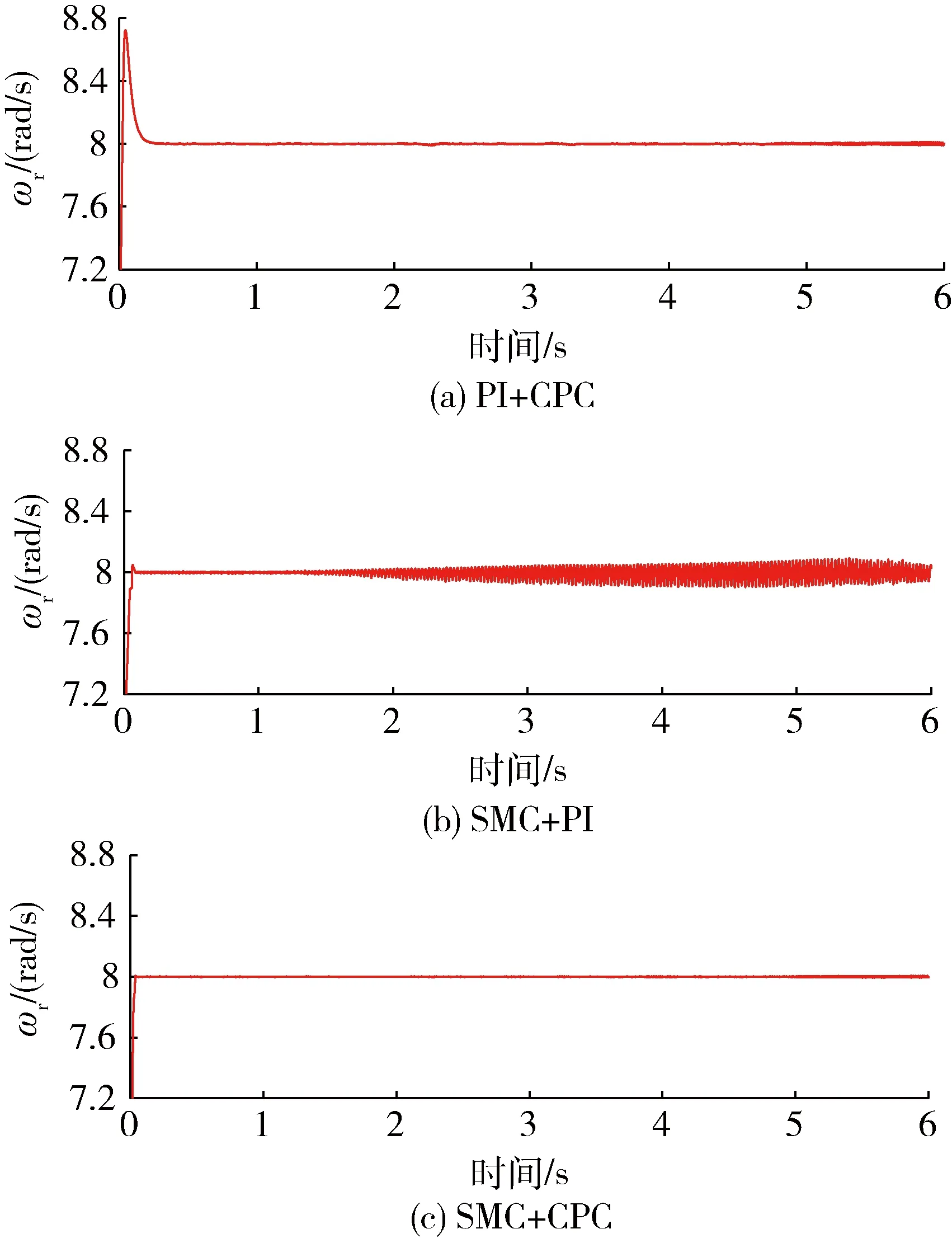
图12 定子电阻漂移对转速的影响Fig.12 The influence of stator resistance drift on rotational speed

从图13可看出，在引入定子电阻漂移扰动后3种方法的转矩均受到了影响并开始下降，本文方法较前两种方法下降幅度有所减小.

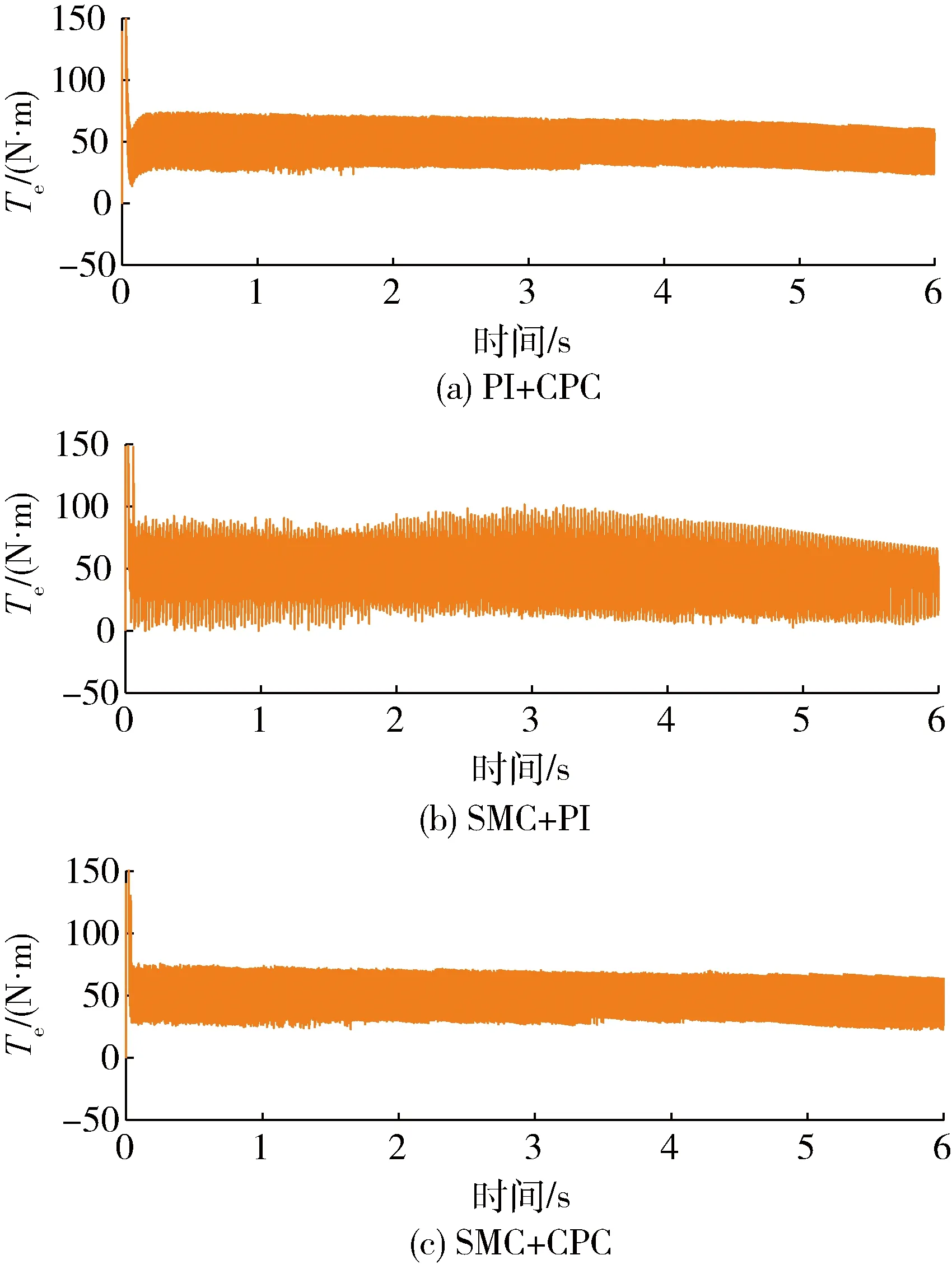
图13 定子电阻漂移对转矩的影响Fig.13 The influence of stator resistance drift on torque

4 结 论

本文将滑模控制用于PMSM矢量控制代替传统PI对转速环进行调节，电流环采用电流预测控制，在Matlab/Simulink平台下搭建仿真模型.

本文方法能实现PMSM调速系统对负载扰动不敏感，使得矢量控制能达到较好的控制效果.

仿真结果表明：滑模控制和电流预测控制(CPC)相结合的方案改善了矢量控制系统的动态性能且无超调，提高了系统响应速度，减小了稳态时转速的高频抖动；保证了PMSM在恒定载荷下三相定子电流的正弦度，通过精准的转速误差调节，改善了PWM波的品质，使得逆变器的开关频率趋于稳定，降低了三相定子电流的谐波含量；使得系统运行对定子电阻漂移扰动具有更好的稳定性，提高了控制系统对电机定子电阻变化容忍度.