基于并行扩展卡尔曼滤波的自主卫星星座导航方法

2021-07-28张原，熊凯，邢琰

空间控制技术与应用 2021年3期

张原，熊凯，邢琰

北京控制工程研究所, 北京 100090

0 引言

航天器导航技术主要用于确定航天器的位置、姿态和速度，这是当前和未来许多航天任务的基本要素，其中，航天器自主导航技术可以降低对地面跟踪观测站的依赖性，增强空间系统的生存能力.

基于星对星跟踪(SST)测量的自主卫星星座导航方法在当前技术条件下具有很高的精度.近些年来有学者给出了使用星间测距技术实现月球卫星自主定轨的方案(LiAISON)，用于在地月三体系统中跟踪卫星[1-3].这种方法只需要进行星间距离测量，而且可以利用星间链路(ISLs)方法实现高精度定位.将多颗地球卫星之间的距离测量结果以及地球卫星与月球卫星之间的距离测量结果相结合，能够提高导航系统的可观度，适用于确定卫星星座的绝对位置.

基于ISLs的星间距离测量容易受到外界干扰，从而导致噪声统计特性的不确定性，通过设计自适应滤波算法可以部分解决模型不确定性问题[4-7].多模型自适应估计(MMAE)作为目前研究最为广泛的自适应滤波方法之一，具有很高的应用价值[8-11].

本文提出一种基于MMAE体系结构的并行扩展卡尔曼滤波器(PEKF).将不同的测量子集分配给各个并行滤波器，各个并行滤波器单独运行，整体状态估计值通过并行滤波器估计值的加权和计算来实现，并行滤波器的权重根据残差序列计算.该方法能够自适应地选择合适的测量值以提高估计精度，同时削弱测量不确定性的不利影响.

1 系统模型

本文所研究的问题是根据测量yj/i,k,(i=1,2,…,N-1,j=i+1,i+2,…N)估计未知状态向量xi,k(i=1,2,…,N)，其中k表示离散的时间点，N表示网络节点数.对于所考虑的自主导航系统，N是星座中的卫星数.状态向量的演化过程由离散非线性模型描述

xi,k=fi(xi,k-1)+wi,k

(1)

其中fi(·)是已知的状态转移函数，wi，k是均值为零的高斯白噪声，其方差阵为

(2)

其中Qi，k(i=1,2，…，N)是半正定矩阵，实际工作中，考虑到数值计算时的截断误差，为保证滤波迭代顺利进行，一般设定Qi，k(i=1,2，…，N)为正定矩阵.

测量yj/i,k与状态向量xi，k和xj，k有关

yj/i,k=hj/i(xi,k,xj,k)+vj/i,k

(3)

其中hj/i(·，·)是已知的非线性测量函数，vj/i，k是零均值高斯白噪声，其方差阵为

(4)

其中Rj/i，k(i=1,2，…，N-1，j=i+1，i+2，…,N)是正定矩阵，假设函数fi(·)和hj/i(·，·)连续可微.如图1所示为存在3个节点和3个传感器的系统网络中，状态向量和测量之间的关系.

图1 状态向量和测量之间的关系Fig.1 Relation between the state vectors and the measurements

递推形式动力学方程和测量为

(5)

其中

(6)

(7)

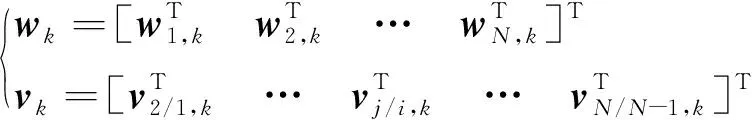
(8)

wk和vk的方差阵分别为

Qk=diag{Q1,k,Q2,k,…,QN,k}

Rk=diag{R2/1,k，…，Rj/i,k，…，RN/N-1,k}

由于研究对象实际中并非强非线性系统，因此对于系统的非线性不作深入研究与探讨.

测量调度的目的是选择测量的子集，使得某些节点的状态向量的估计误差最小，这通过最小化适当的代价函数来实现.对于非线性随机系统，可以采用Cramer-Rao下界(CRLB)作为性能度量指标[12-13].CRLB提供了均方估计误差(MSE)的一个下界，可用于评估滤波器的性能.通常，较小的CRLB值意味着更精确的状态估计，而且这种性能度量方式具有广泛的适用性，并不只是针对某一种特定的滤波器.

作为状态估计的误差协方差矩阵下界的CRLB具有以下形式

(9)

(10)

如果忽略过程噪声，则可以简化为

(11)

在计算CRLB时是不考虑模型不确定性的，而在测量噪声统计特性不确定的情况下，对于某一个具体的滤波器而言，很难达到理论上的极限精度.

当对噪声统计特性有准确的先验知识时，基于理想模型设计的滤波器性能将随着测量的增多而提高.但是，如果噪声统计信息未知或不准确，则随着测量的增多，滤波性能可能会下降.应对这种情况，需要设计一种有效的滤波算法来自适应地选择合适的测量值以获得良好的估计精度.

2 并行扩展卡尔曼滤波器

为了使多源测量融合技术适用于具有潜在的噪声统计不确定性的非线性系统，提出一种PEKF算法，通过残差来计算相应的权重，来降低受干扰测量在滤波器估计中的比重，提高其他测量所占的比重从而降低干扰带来的影响.详细步骤如下所述.

步骤1.初始化

对于存在N个节点的系统，设置N+1个并行滤波器.状态向量初始化为

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

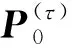
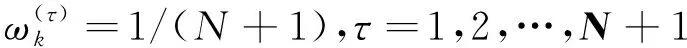
(20)

步骤2.并行滤波

(21)

(22)

(23)

(24)

从式(21)～(24)中不难看出，与第i个节点相关联的测量不包括在第i个并行滤波器的测量子集中，而第(N+1)个滤波器利用网络中所有可用的测量值.滤波器采用扩展卡尔曼滤波(EKF)方法设计实现，滤波方程不再赘述.

步骤3.权重更新

(25)

并且

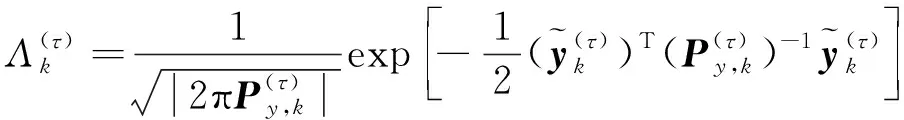
(26)

式(20)所示的滤波器初始权重表示每一个并行滤波器初始时具有相同的权重，后续滤波器工作中根据测量残差进行调节更新.但是如果存在与各并行滤波器重要性相关的先验知识，可以根据先验知识设置不同的滤波器权重初值.

如(25)和(26)所示的自适应率的收敛性可以用类似于文献[14]方法来证明.随着滤波迭代计算过程的进行，上述自适应率为受不确定性影响相对较小性能更好的滤波器提供更高的权重，而为受不确定性影响相对较大性能最低的滤波器权重几乎为零.

步骤4.状态组合

PEKF算法的最后一步是根据权重来组合并行滤波器的估计值.完整的状态估计仅用于输出，在PEKF算法中不做递归使用.由于不同并联滤波器的状态向量维数不同，采用归一法计算局部权值[15].第i个节点的局部权重计算如下:

(27)

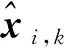
(28)

3 自主卫星星座导航

本文所研究的星座自主导航系统的任务是利用卫星间距离测量的时间序列确定地球卫星和月球卫星的绝对位置.通过月球卫星和多颗地球卫星建立导航网络，距离的测量基于星间链路(ISLs)方法.星座如果有足够精确的测量，可以达到较高的定位精度. ISLs方法容易受到外界干扰，使得噪声统计特性存在不确定性，这也是本文研究所要解决的问题.图2所示为一个典型的星间链路星座的结构，其中包含了3个地球卫星和1个月球卫星.

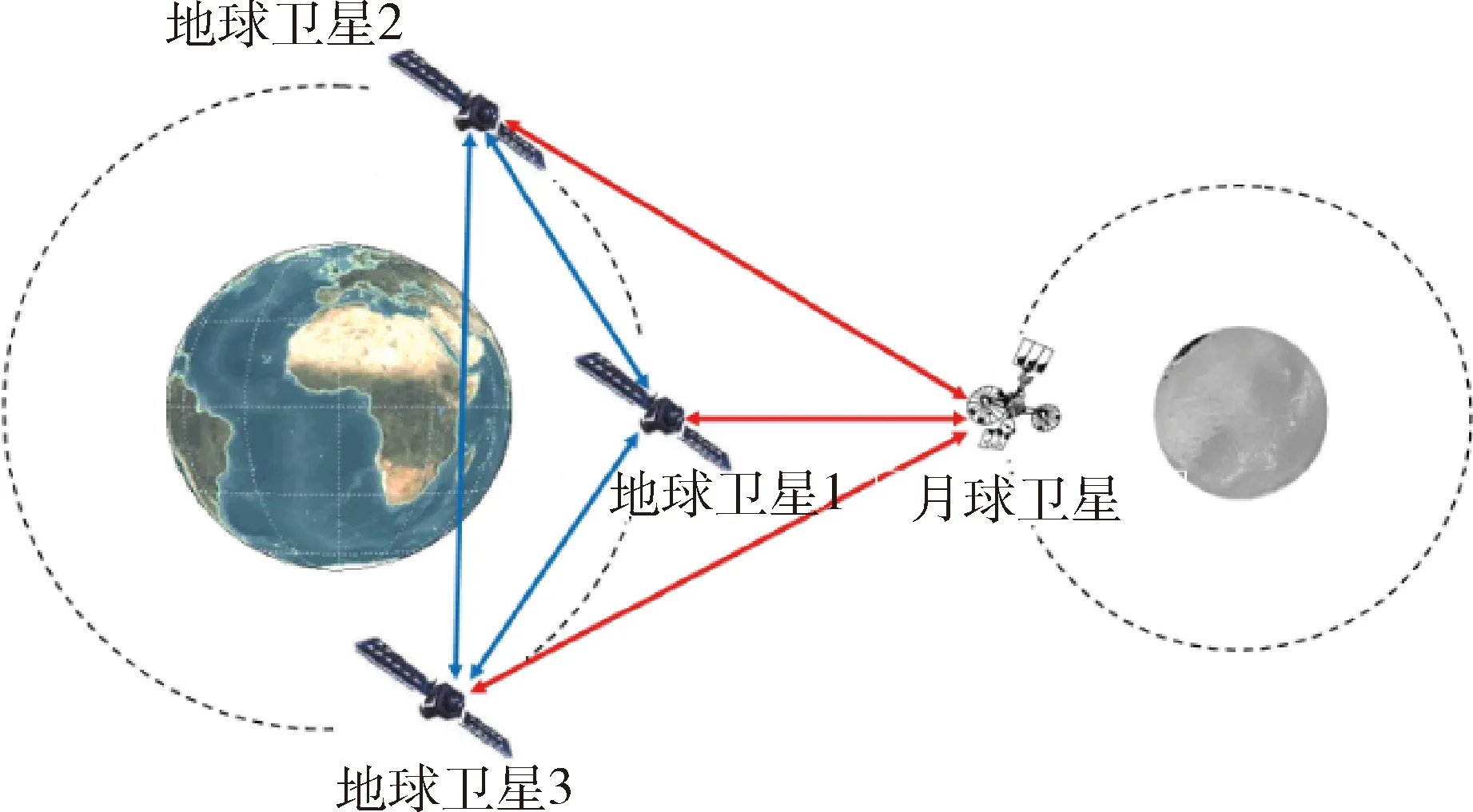
图2 星间链路星座示意图Fig.2 Concept of satellite constellation with inter-satellite links

对于由N颗卫星组成的星座，在(1)和(3)中描述了自主导航系统的模型结构.对于第i个卫星，状态向量xi,k由相应的卫星位置和速度矢量组成.

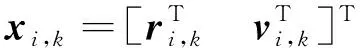
(29)

其中ri，k和vi，k是地心惯性系(ECI)中定义的位置和速度矢量.对于地球卫星，状态转移函数建模如下[16]

(30)

其中T是轨道外推的步长，μ是地球的引力常数，p(ri,k-1)表示卫星的摄动加速度.摄动加速度包括了地球非球形质量分布的引力加速度、大气阻力、太阳辐射压力和月球太阳引力摄动等.月球卫星的状态转移函数与地球卫星的状态转移函数形式相似，这里省略.

利用地球卫星与地球卫星、地球卫星与月球卫星之间的距离测量值进行融合导航.测量函数如下

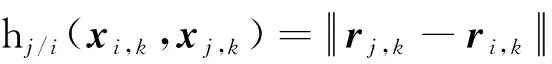
(31)

式中‖·‖表示欧几里德范数.

4 仿真结果

通过数值仿真测试PEKF算法在自主卫星星座导航系统中的性能，并与EKF和传统MMAE算法比较来说明结果.

以4颗卫星组成的星座自主导航系统为例：3颗卫星在地球轨道，另一颗卫星在月球轨道.卫星的初始轨道要素见表1.表中月球卫星的轨道要素是相对于月球的.假设卫星在小偏心率的近圆轨道飞行.

表1 星座卫星的初始轨道要素Tab.1 Initial orbit elements of the satellites in constellation

通过初始轨道要素，利用高精度轨道仿真器产生卫星的真实轨道数据，并根据真实轨道模拟产生星间距离测量结果.星间距离测量的更新周期为10 s，在正常情况下，测量噪声为高斯噪声，标准差为距离20 m，速度0.005 m/s.干扰条件下，对于任意一个地球卫星的测量噪声而言，增大与其相关的距离测量噪声，初始导航误差的标准差设置为三轴相等，均为位置50 m.模拟运行时间为2 天.

考虑到地球附近的卫星易受到干扰影响，在PEKF算法中设置了4个并行滤波器，其中一个滤波器设计为利用所有的测量，另外3个滤波器设计成与地球卫星和月球卫星的不同组合相关的测量子集.为了进行公平的比较，对EKF，MMAE和PEKF设置相同的初始状态误差协方差和相同的过程噪声协方差.

对于EKF和PEKF，测量噪声协方差设置为标称值20 m.对于MMAE中的4个并行滤波器，测量噪声的标准差分别设置为10 m、20 m、30 m和40 m.

无干扰条件下，EKF、MMAE和PEKF的位置估计误差曲线如图3～图5所示，其中虚线表示3σ误差界，实线表示估计误差.

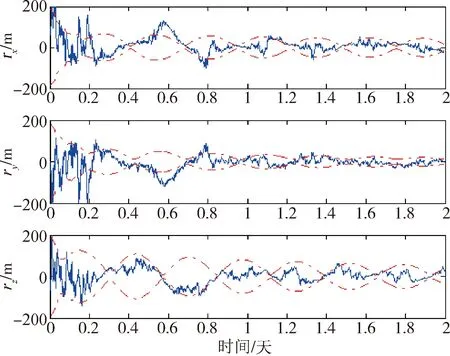
图3 EKF的位置估计误差Fig.3 Position estimation error curve of EKF

图4 MMAE的位置估计误差Fig.4 Position estimation error curve of MMAE

图5 PEKF的位置估计误差Fig.5 Position estimation error curve of PEKF

从图中可以看出，在没有噪声干扰的情况下PEKF的估计结果优于EKF.MMAE算法能够在一定范围内适应测量噪声协方差的变化，所以MMAE算法的性能介于其他两种算法之间.但是总体而言三者区别并不大.

为了评估所提出的滤波算法对噪声统计不确定性的适应性，引入干扰.对某一个地球卫星，引入标准差为0.08 m/s的白噪声作为干扰噪声.EKF、MMAE和PEKF的位置估计误差曲线如图6～图9所示.

图6 EKF的位置估计误差Fig.6 Position estimation error curve of EKF

图7 MMAE的位置估计误差Fig.7 Position estimation error curve of MMAE

图8 PEKF的位置估计误差Fig.8 Position estimation error curve of PEKF

仿真结果显示存在干扰时EKF和MMAE的估计误差显著增加.EKF的估计误差大于3σ，表明EKF在存在模型不确定性的情况下滤波器性能受到影响.由于随机干扰不包括在预先设置的模型集中，MMAE的性能也不理想.事实上，很难在MMAE的模型集中准确地涵盖所有可能的模型，因为很难获得所有可能的不确定性的充分先验知识，而且不确定参数组合的数目受到应用系统的限制.相比EKF和MMAE，PEKF的性能更好，因为仿真研究中不受不确定性影响的测量子集对应的并行滤波器在算法中占主导地位，说明了权重更新和状态组合方法在干扰条件下的有效性.

图9展示了PEKF算法中的权重更新过程，图中可以看出，在经过一定时间的迭代后，引入噪声干扰的测量子集相关的权重降低，滤波所使用的测量信息的绝大部分来源来自无干扰的测量子集，表现了测量调度能力.