仿壁虎刚毛阵列对卫星表面吸附能力模型与计算
2021-07-28王杰娟于小红周雯雯
罗 剑, 王杰娟, 于小红, 周雯雯
航天工程大学, 北京 102206
0 引 言
受自然界中壁虎能轻易攀附在光滑的墙壁的启发,国内外对壁虎附着机制和壁虎刚毛结构特征开展了深入研究.美国AUTUMN等[1]于2000年在《Nature》上发表的论文指出,壁虎的粘着力是由脚底绒毛与物体表面分子之间产生的范德瓦尔斯力(van der Waals forces)累积而成的.范德瓦尔斯力是中性分子彼此距离非常近时,产生的一种微弱引力.壁虎趾面上有一系列排列整齐的皮瓣,皮瓣宽约400~600 μm,皮瓣上是倾角近似一致的刚毛阵列,每根刚毛直径5 μm,长约100 μm,刚毛末端又分岔为100~1 000根绒毛,每根绒毛的半径大约在0.2~0.4 μm之间,这些微细的毛发与接触面之间产生的“范德瓦尔斯力”形成了惊人的吸附力.相对于其他粘着机理(如真空吸附、静电吸附和化学吸附等)具备明显优势.真空吸附对卫星表面粗糙度要求高,且太空环境没有气体能够形成压力;静电吸附要求接触面具有导电性,且静电力较小,较难吸附;化学粘附粘胶容易挥发、固化,在太空环境中难以实现[2].壁虎具有粘附力大、对接触面的形貌和材质适应性强、不会对物体表面造成损伤、自洁、稳定等优点,是一种干性吸附,非常适合应用于微机器人的粘附爬行机构中.其粘着机理对航天机器人脚掌的研制和开发具有重要启发意义.目前制作仿壁虎刚毛阵列的一些材料在航天领域的应用较为广泛,在参考文献[3]中指出,仿壁虎刚毛材料有硅橡胶、聚亚胺酯、多壁碳纳米管、聚酯树脂、聚酰亚胺、人造橡胶、环氧树脂、聚二甲基硅氧烷、聚氨酯与对苯二甲酸乙二酯、聚甲基丙烯酸甲酯等.其中一些聚合物复合材料已经广泛应用于航空航天领域,且技术成熟.由参考文献[4-6]可见,仿壁虎刚毛阵列具有太空应用的可行性.从参考文献[7]可以看出,聚酰亚胺薄膜材料已在航天器表面、卫星蜂窝结构、透波和隔热体系中广泛运用.在本章中,主要分析由聚酰亚胺制成的仿壁虎刚毛阵列吸附脚[8],也是目前制作刚毛的主要材料之一.
1 单根刚毛与光滑表面黏着力模型与计算
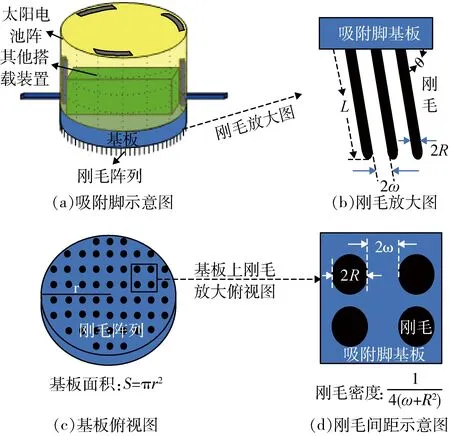
图1 吸附脚组成示意图Fig.1 Schematic diagram of adsorption foot composition
刚毛阵列与接触表面之间的黏着力来自范德瓦尔斯力(van der Waals forces).由参考文献[9-10]得知,单根刚毛与光滑表面的黏着力为
Fvdw=HR/(6D2)
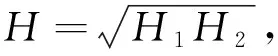
刚毛材料为聚酰亚胺,与刚毛阵列接触的为卫星表面涂层材料,由参考文献[11-12]可知,卫星表面涂层材料主要有C/C复合材料、聚合物复合材料和陶瓷/金属功能梯度热防护材料等.在本章中,卫星表面涂层材料也以聚酰亚胺为对象进行分析,所以,H=H1=H2.计算Hamaker常数的经验公式为H=2.1×10-21γ,其中γ为材料的表面能[11].需要特别注意的是,此经验公式是数学规律公式,并不代表实际的物理关系,运用时H的单位为J,表面能γ的单位为mJ/m2或mN/m.
固体材料表面能γ与热力学温度T有经验公式γ=γ0+ΓT,Γ为材料的表面能温度系数,γ0为标称温度下材料的自由表面能,Γ的单位为mN/(mK),γ0的单位为mJm-1,T的单位为K[14-15].由参考文献[14]可查得聚酰亚胺在标称温度时的自由表面能为γ0=46.5 mN/m,Γ=-0.065 mN/(mK).
在不考虑接触表面粗糙度的情况下,根据Hamaker常数、表面能和热力学温度之间的经验公式,可将单根刚毛与光滑表面的黏着力转化为
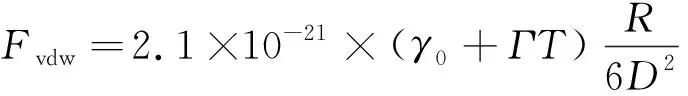
(1)
同理,式(1)为数学经验公式,不代表物理关系,计算时γ0单位为mN/m,Γ单位为mN/(mK),T单位为K,R和D单位为m,计算所得的Fvdw值的单位为N.
整个刚毛阵列与与光滑表面的黏着力为:
F=n×Fvdw
根据式(1)可以看出,当刚毛末端半径为R固定时,单根刚毛与光滑表面的黏着力随热力学温度的变化L=6 μm而改变.如果刚毛阵列有关参数固定,R=0.6 μm、2ω=3.5 μm、S=πr2=22.09 cm2、刚毛总数n=108根、r=2.651 7 cm.由参考文献[17-19]可知太空环境温度t的变化范围为-200℃~70℃,可以计算出黏着力随温度t的变化情况如图2所示.需要注意的是,在进行仿真计算时,温度t需要转换为热力学温度T=t+273,单位为K,同时注意其他各物理单位的一致.
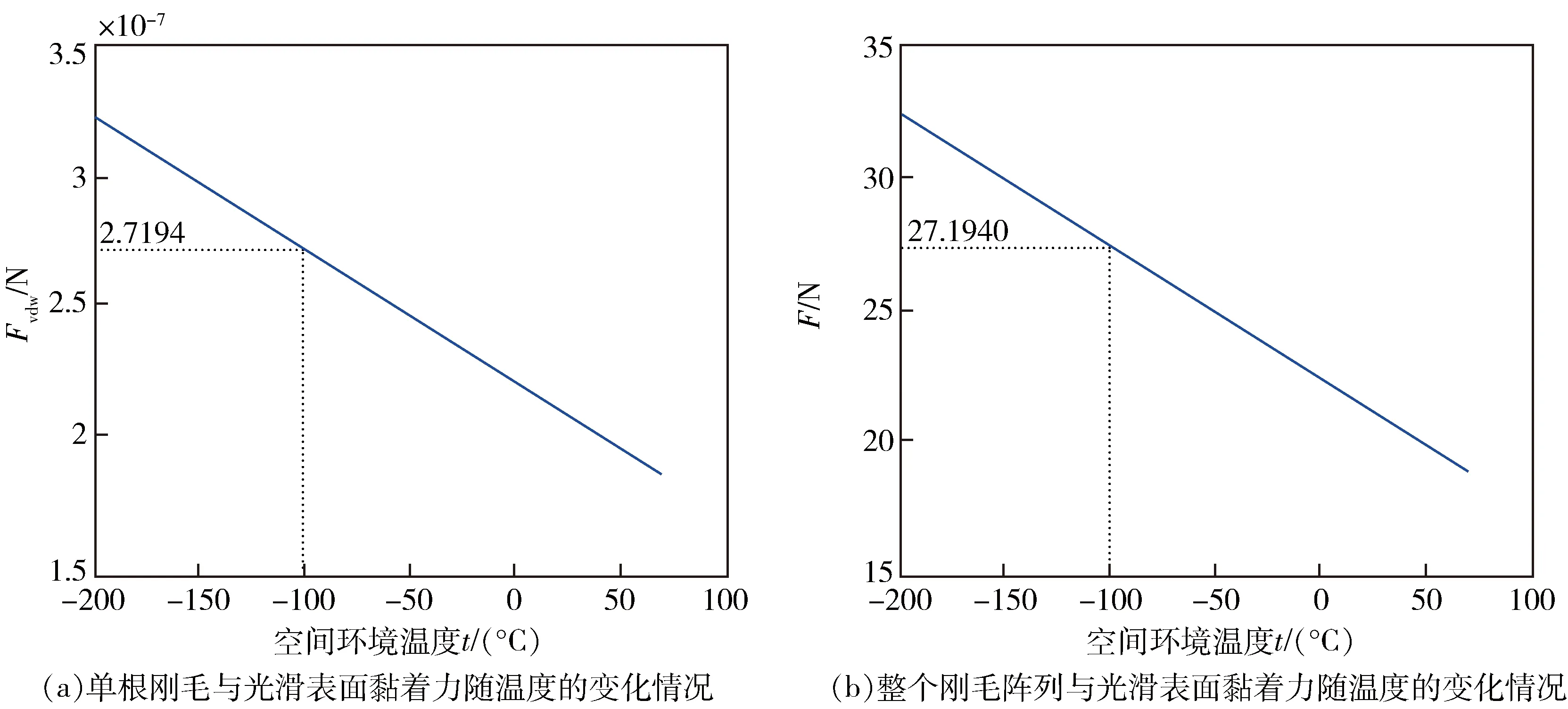
图2 与光滑表面间的黏着力随太空环境温度t的变化情况Fig.2 Adhesion to a smooth surface as a function of ambient space temperature t
可以看出以下结论:
1)黏着力随着太空环境温度的降低而增加,借助仿壁虎刚毛阵列产生的黏着力在太空环境中具有显著应用价值,是附着功能的有效手段.
2)单根刚毛与光滑表面黏着力Fvdw为微牛级(μN),由108根刚毛组成面积为S=22.09 cm2的刚毛阵列与光滑表面接触时能够产生的实际黏着力F为几十牛顿,与参考文献[20]中测量的壁虎吸附力结论一致.
2 卫星粗糙表面分布模型与接触概率与计算
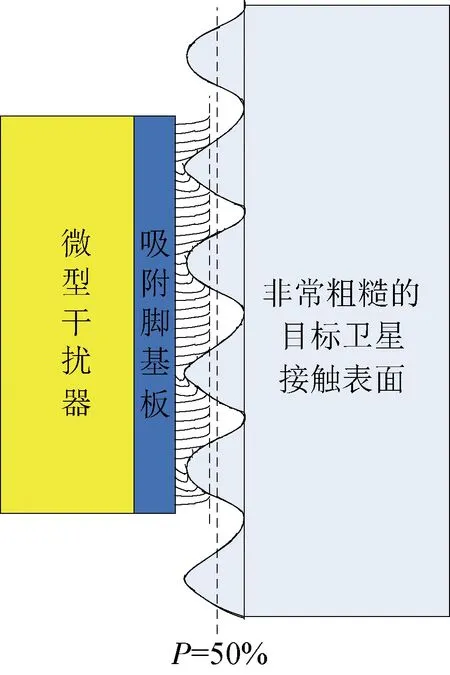
卫星表面长期暴露在外,由于各种辐射和强温差使得卫星表面粗糙不平,不能视为光滑表面.如图3所示,为刚毛阵列与卫星表面的接触模型.
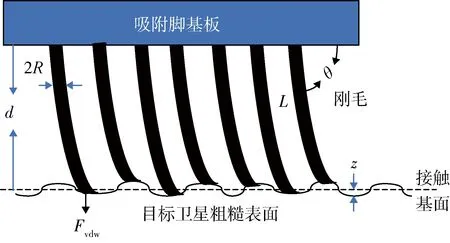
图3 刚毛阵列与卫星表面的接触模型Fig.3 Contact model of bristle array and satellite surface
由随机物理现象造成的粗糙表面峰值分布服从高斯分布规律,可将卫星粗糙表面微凸起峰高视为高斯分布
其中,z为卫星粗糙表面轮廓与接触基面之间的距离(单位为μm),σ为卫星表面粗糙度(单位为μm),设d为吸附脚基板与接触基面之间的距离(单位为μm).则刚毛将会与高度z大于d-Lsinθ的所有微凸起发生接触,θ为接触时刚毛与基板之间的夹角(单位为°),接触概率为
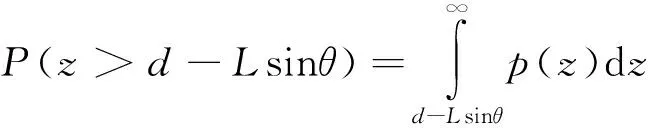
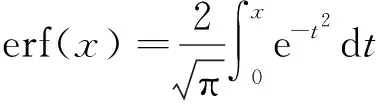
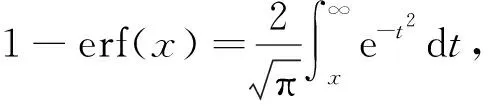
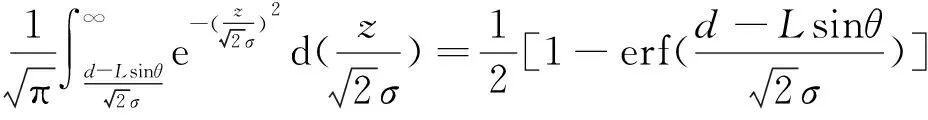
(2)
由式(2)可见,当L与θ固定时,接触概率P随着粗糙度σ和基板与接触基面之间的距离d的不同而变化,如图4所示,为L=6 μm,θ=30°(θ大约为30°时,黏着力最大[9,21],接触概率随粗糙度σ和间距d的变化情况.
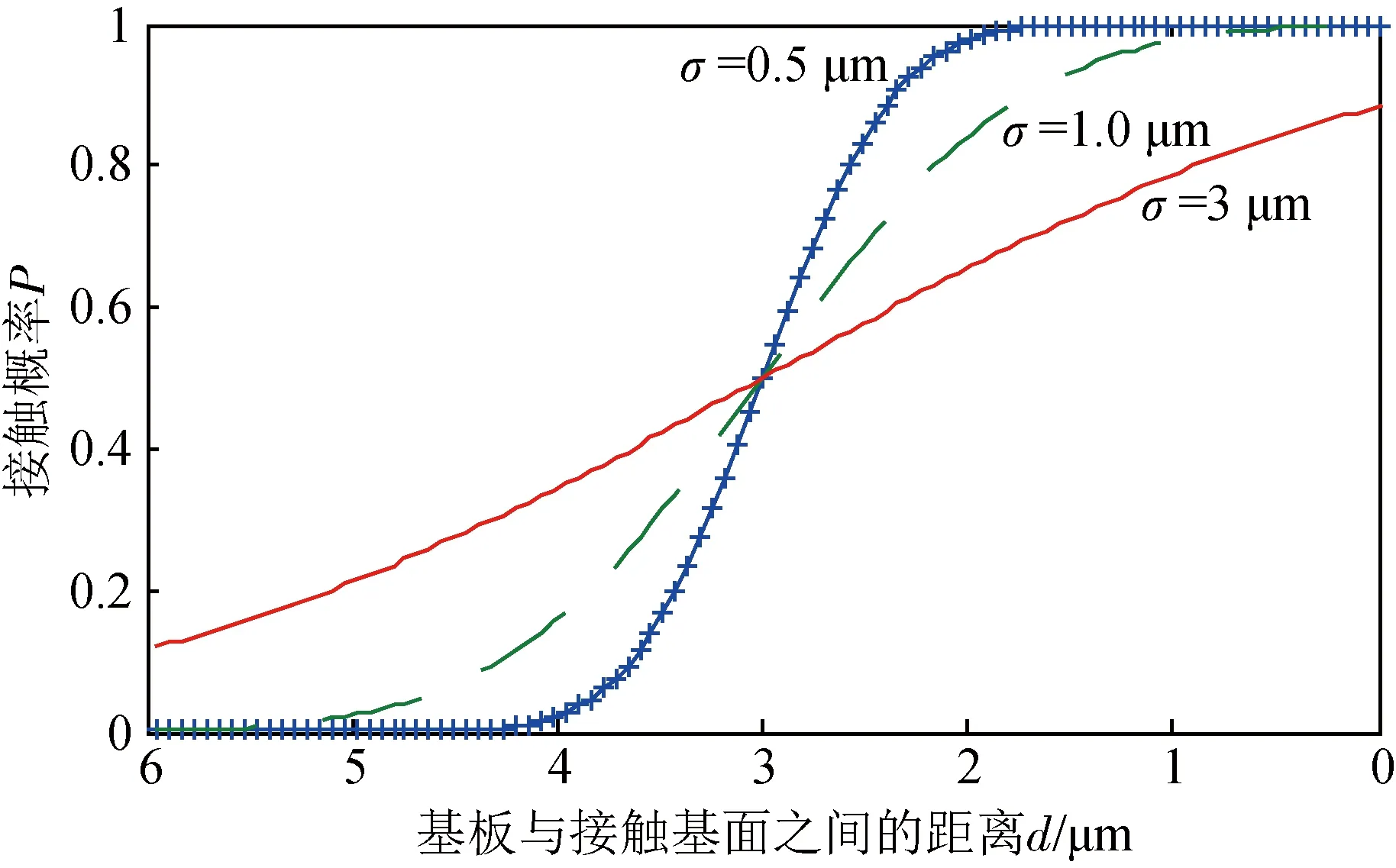
图4 接触概率随粗糙度σ和间距d的变化情况Fig.4 The variation of contact probability with roughness σ and spacing d
可以看出以下结论:
1)接触概率P随着间距d的减小而增大,间距d越小,基板与接触基面越近,能够与卫星表面接触的刚毛越多,接触概率P越大.
2)当间距d>Lsinθ时,接触概率P随着粗糙度σ的增大而增大,且接触概率小于50%.如图5所示,为d>Lsinθ的情况,可以看出,粗糙度越大,能够与卫星表面接触的刚毛越多,接触概率P越大.
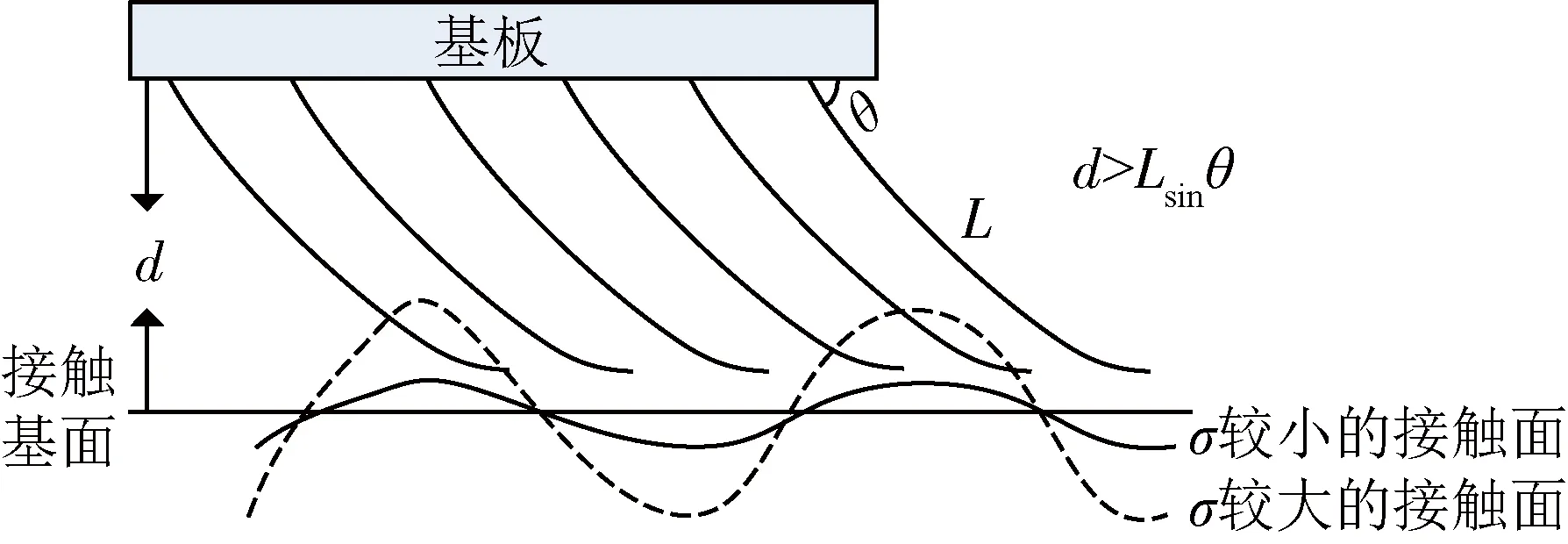
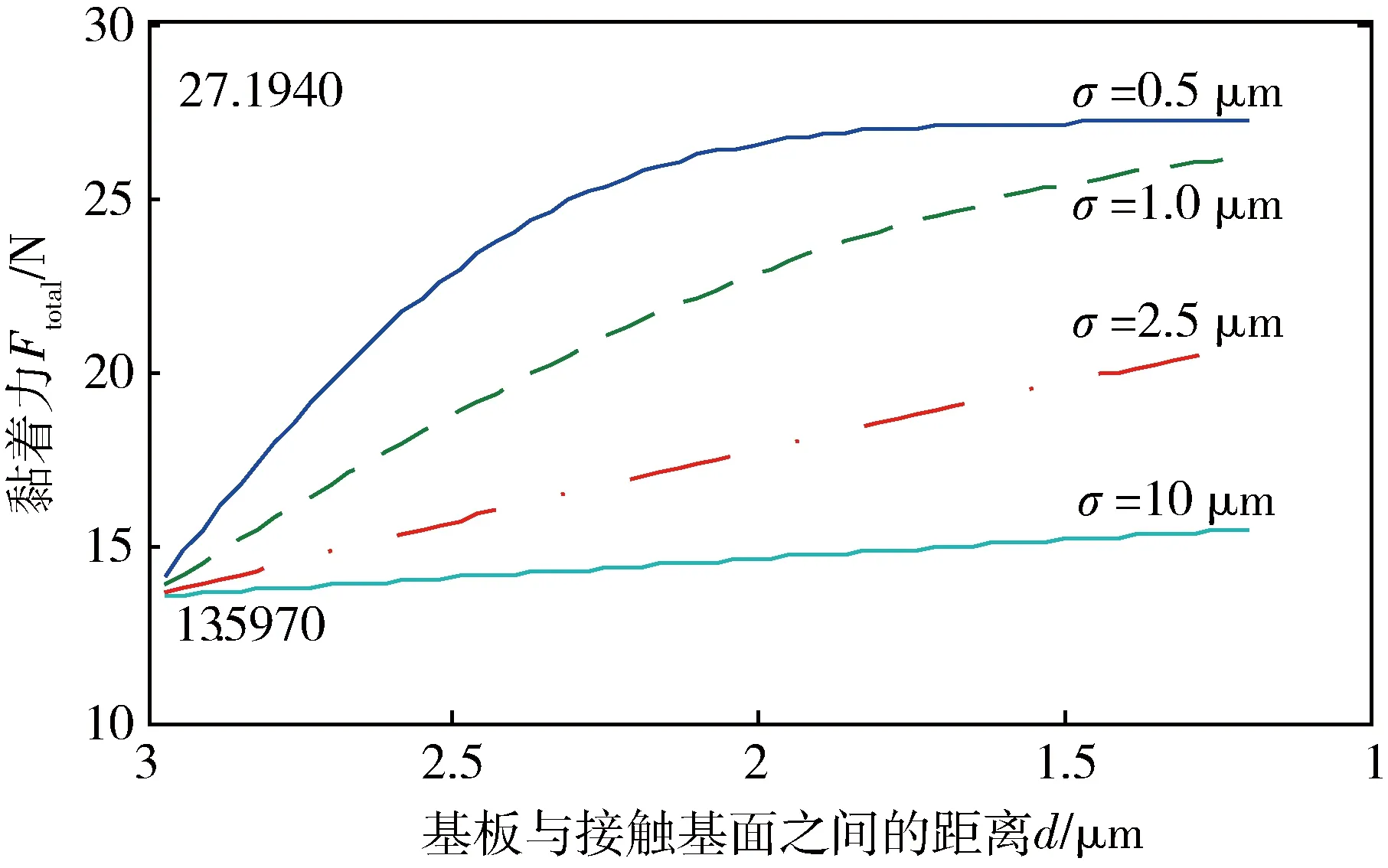
图6 d 5)为了使接触概率大于50%,间距d最好小于Lsinθ,即应当尽可能地使刚毛能够充分接触到卫星表面. 根据单根刚毛与光滑表面的黏着力Fvdw、刚毛总数n和接触概率P,可以得到整个刚毛阵列与卫星粗糙表面黏着力为 Ftotal=nFvdw×P(z>d-Lsinθ)= (3) 如果所有参数与前面设置相同,即L=6 μm,R=0.6 μm,2ω=3.5 μm,S=πr2=22.09 cm2,n=108,θ=30°,根据式(1)得到在太空环境温度t=-100℃时,单根刚毛与光滑表面的黏着力Fvdw=2.719 4×10-7N,整个刚毛阵列与光滑表面的黏着力nFvdw=27.194 N,根据式(3)可以计算出刚毛阵列与不同粗糙度的卫星表面的黏着力Ftotal随间距d的变化情况如图7所示.粗糙度分别为σ=0.5 μm、1.0 μm、2.5 μm和10 μm;间距d的范围为2R 图7 与卫星粗糙表面间总黏着力Ftotal随间距d和粗糙度σ的变化情况Fig.7 The variation of the total adhesion Ftotal with spacing dand roughness σ between the satellite and the rough surface 可以看出以下结论: 1)当间距d 2)在向卫星投放吸附脚时,应尽量使刚毛接近卫星表面,减小吸附脚基板与接触基面的距离d,当d 3)刚毛阵列对卫星表面的粗糙度有着较强的适应能力,只要间距d 图8 刚毛阵列对粗糙接触表面的吸附能力示意图Fig.8 Schematic diagram of the adsorption capacity ofbristle array on rough contact surface Ftotal接近nFvdw/2,完全能够满足在太空失重环境中将干扰型吸附脚黏着在卫星表面的要求. 本文通过单根刚毛对光滑表面附着力计算模型和卫星粗糙表面分布模型与接触概率,推导得出刚毛阵列与卫星粗糙表面黏着力模型,通过仿真分析,说明了刚毛阵列黏着力与卫星表面粗糙度、吸附脚基板与接触基面的距离的关系,计算结果表明在太空失重环境中能够将干扰型吸附脚黏贴在卫星表面,进而实现攀附,说明了仿壁虎刚毛阵列具有在空间非合作目标操控应用的可行性.3 刚毛阵列与卫星粗糙表面黏着力模型与计算
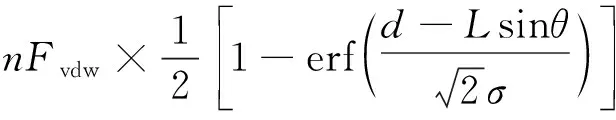
4 结 论
