含球面副并联机构的可调工作空间求解
2021-07-26沙鑫美吕小祥
沙鑫美,吕小祥
(1.三江学院机械与电气工程学院,江苏 南京 210012;2.江苏南京热电工程设计院,江苏 南京 210012)
1 引言
近些年来,并联机器人已经成为装备制造、能源发展、航天航空等领域必不可少的组成部分[1],3-PSR并联机构是一种少自由度的1T2R 并联机构,该机构具有较好的力学性能,承载能力强,故而研究者众多。文献[2]提出了一种新的3自由度3-PRS空间并联机器人,并对其位置正反解,奇异性和工作空间进行了研究;文献[3]在理论推导的基础上,对空间3自由度并联机器人3-RPS 并联机构的虚拟样机进行了运动学分析;文献[4]在求得3-PRS并联机构的位置逆解的基础上,采用转化求解对象法对其位置正解进行了解析,方法简单而有效。
在对并联机构运动学解析的基础下,工作空间是衡量并联机构性能的重要指标[5],文献[6]用Matlab 软件对3-PRS 并联机器人的工作空间进行研究和仿真;文献[7-10]分别以并联机构为研究对象,对机构的工作空间进行了分析研究及仿真,并在此基础上研究了运动副布置、机构结构参数对机构工作空间的影响;文献[11]使用三维搜索法,基于该机构的结构参数提出了6-3-3并联机构在给定姿态下工作空间分析的计算机仿真方法,并用工作空间截交面的截面形状检验其内部是否存在空腔。但是上述3-PSR并联机构的工作空间是有局限性的,故引入的可调工作空间并联机构,该机构具有可以满足机构的不同工作环境,具有很大实用价值。在可调机构方面,文献[12]用复数方法解决了可调机构的构型综合问题。在构建含球面副可调空间3-PSR并联机构的基础上,建立该机构的几何模型和运动学方程;然后采用Simulink控制函数建立可变参数,引入影响因子λ,用SimMechanics法对具有可调空间的3-PSR并联机构的工作空间进行分析求解并展开研究,同时结合结构参数对机构空间的影响进行分析,分析研究滑动副的运动范围对工作空间的体积的影响。
2 3-PSR并联机构几何模型
为3-PSR 并联机构简图,如图1 所示。该机构包括动平台(上正三角平台R1R2R3)和静平台(下正三角平台A1A2A3)以及三条完全相同的支链:一个移动副(P)、一个球副(S)与一个转动副(R)依次联接而成,三支链成中心对称分布。该机构的静平台通过移动副Pi与球副Si相连,转动副Ri通过连杆li与球副Si相连,动平台与连杆li通过转动副Ri相连(其中i=1,2,3)。根据机构的几何特征,故在静平台A1A2A3的几何中心点O处建立固定坐标系为OXYZ,在动平台R1R2R3的几何中心点o处建立如图动坐标系为:oxyz;动坐标系固接在动平台上,伴随着动平台运动,中心点o处坐标值为(xR,yR,zR)。设静平台的外接圆直径为D,动平台的外接圆直径为d,连杆li与竖直面的夹角为θi,连杆li与竖直面的夹角为φi,连杆li的长度为l。滑动副的行程为Li(其中,i=1,2,3)。
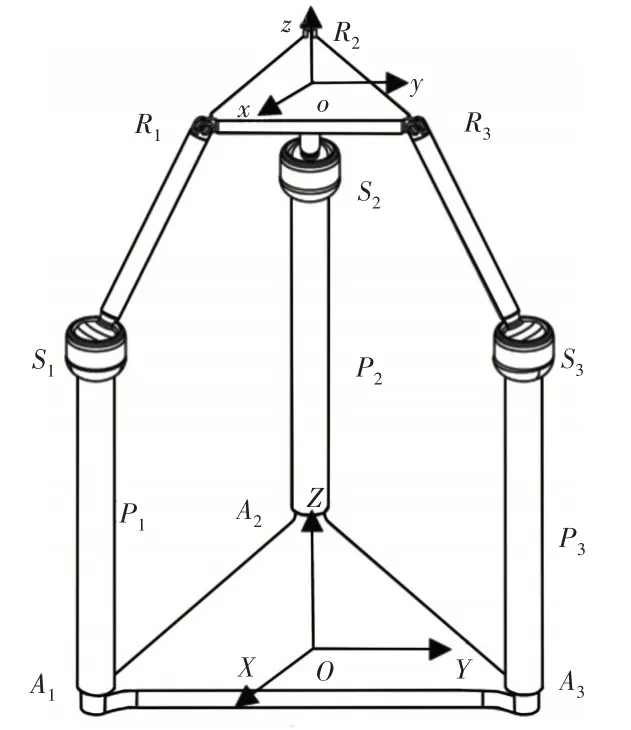
图1 3-PSR并联机构简图Fig.1 3-PSR Parallel Mechanis
3 含球面副并联机构运动学求解
点Ri和Ai关于静坐标系{O}和动坐标系{o}的位置矢量分别表示为ORi和oAi,如图1所示。则有:
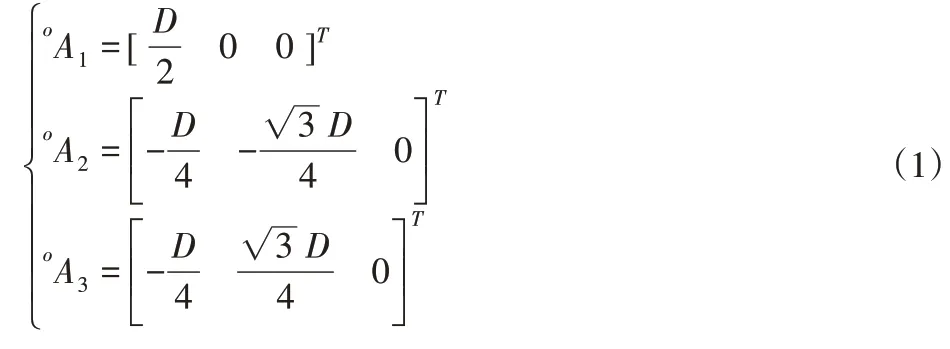

其中,三个列向量分别表示动坐标三个坐标方向在定坐标系中对应的方向余弦。故该矩阵为正交矩阵,故得:

静平台连接底端Ai中心到对应支链的球铰中心的长度为Li,则有:

根据旋转矩阵法式(3)~式(4)可得,局部坐标系相对于全局坐标系的三个坐标轴γ,β,α后得到旋转后各方向余弦矩阵的为:

由式(13)根据3-PSR并联机构的各结构参数之间的关系计算式,可以求解机构三个驱动杆的运动情况。根据3-PSR并联机构运动学方程以及动平台边长不变原理可得该机构的约束方程:
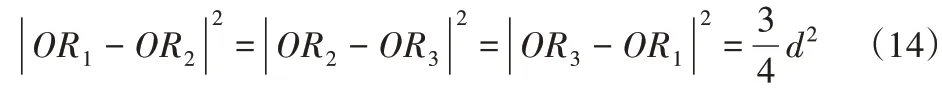
根据实际的工程应用,机构的球副Si的实际转角转动受限。为了避免杆件在转动过程中发生干涉,则该机构球副的转角约束条件如下:

该机构滑块驱动副行程限制约束条件如下:

式中:Li,Limin,Limax—第i个支链滑块Pi的移动距离、最小和最大极限行程。机构的转动副Ri的转角在实际转动中受限,其转角约束条件如下:

故由式(1)~式(14)以及约束条件式(15)~式(17)共17个方程中,除了已知参数和结构参数外,联立求解方程组,可求得机构活动平台的位置参数。该机构滑块驱动副行程限制约束和连杆的杆长约束对机构的工作空间影响较大,故在分析的过程中以滑杆的移动行程和连杆杆长作为变量。设定滑杆的移动行程和连杆杆长之比为λ。
4 SimMechanics模型构建
利用数学工具Matlab中的SimMechanics模块对并联机构系统进行建模,其可为多体动力机械系统及控制系统提供直观有效的建模分析手段。在Simulink工具箱中建立3-PSR并联机构多体动力机械系统图,如图2所示。
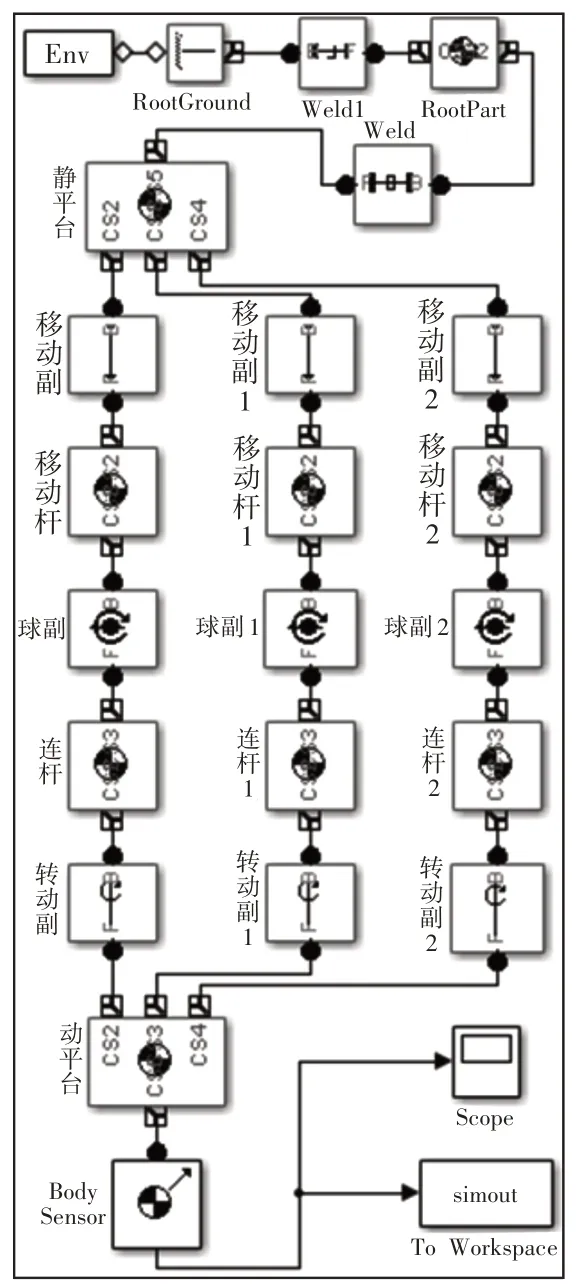
图2 3-PSR并联机构多体动力机械系统图Fig.2 SimMechanics Structure of 3-PSR Parallel Mechanism
根据影响因子的定义,采用PID 控制3-PSR 并联机构的滑杆的移动行程和连杆杆长之比λ。在Simulink 工具箱中建立机构多体动力参数控制系统,如图3所示。机构SimMechanics结构框图,如图2所示。Env用来设置工作环境;Body Sensor来测量刚体的数据,Scope采集到的数据保存到Workspace中,以供后处理使用。在控制系统中,我们对该机构的影响因子λ实现PID控制,从而达到机构可调工作空间的目的。
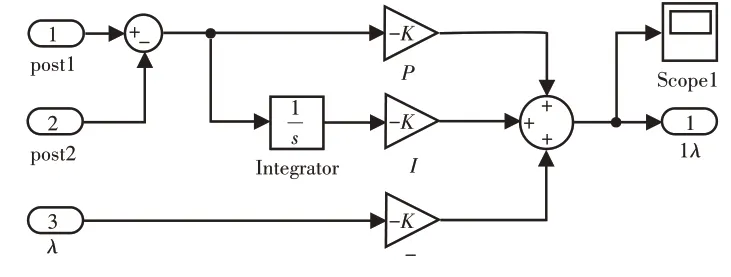
图3 机构多体动力参数控制系统图Fig.3 Multi-Body Dynamic Parameter Control System Diagram
5 可调工作空间算例分析
根据机构的运动学以及影响因子的分析,机构的位置工作空间,由球副和转动副转角限制的两侧边界,最大、最小杆长限制的上下边界组成。该机构滑块驱动副行程限制约束和连杆的杆长约束对机构的工作空间影响较大,故在分析的过程中以影响因子λ作为变量。通过PID控制来实现影响因子λ的调节,这样即达到了计算工作空间的目的,也实现了可调工作空间的求解,在实际机构的应用中起到了理论和算例的双重支撑。
假定3-PSR 并联机构的基本尺寸,静、动平台直径为D=100,d=50,夹角θi的初始值为60°,夹角φi的初始值为0°,连杆的长度li=100,滑动副的初始行程为Li=160(其中长度单位均为mm,i=1,2,3)。3-PSR并联机构的位置工作空间就是求解该机构动平台中心点o可达空间的所有点的集合。根据机构SimMechanics的结构框图可得机构在不同λ值下的工作空间图。
从图4~图7中可得:3-PSR 并联机构的可调位置工作空间随着λ的增大,该机构的可达工作空间X,Y,Z向的数值也随之变大,从中比对可知,机构的可调位置工作空间范围有限,形状规整分布均匀;在X和Y向的工作空间呈对称形式,其工作空间的体积随着影响因子λ的值的变大而变大,其变化曲线,如图8所示。
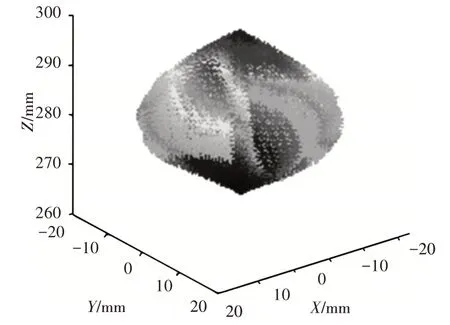
图4 λ=0.3时3-PSR并联机构位置工作空间图Fig.4 Position Workspace of 3-PSR Parallel Mechanism when λ=0.3
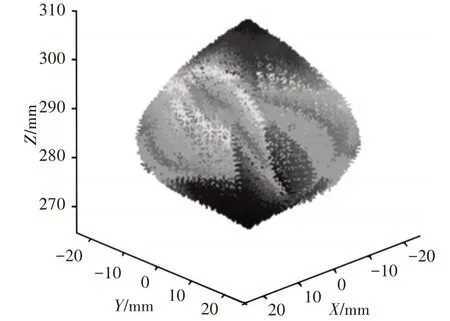
图5 λ=0.4时3-PSR并联机构位置工作空间图Fig.5 Position Workspace of 3-PSR Parallel Mechanism when λ=0.4
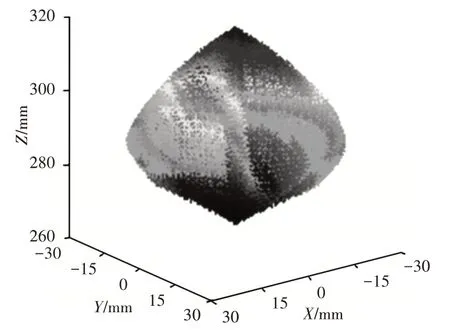
图6 λ=0.5时3-PSR并联机构位置工作空间图Fig.6 Position Workspace of 3-PSR Parallel Mechanism when λ=0.5
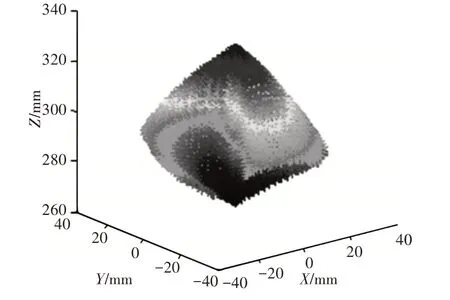
图7 λ=0.6时3-PSR并联机构位置工作空间图Fig.7 Position Workspace of 3-PSR Parallel Mechanism when λ=0.6
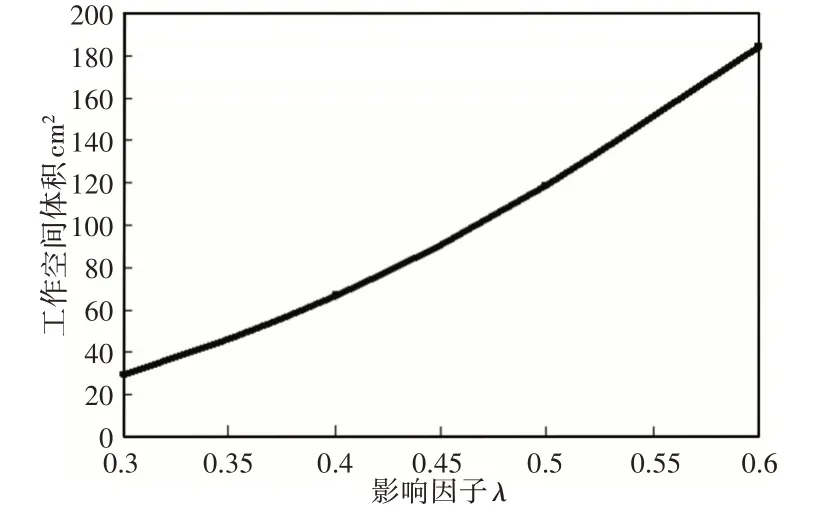
图8 工作空间体积随影响因子λ变化图Fig.8 Variation of Workspace Volume with Influence Factor λ
6 结语
主要针对含球面副并联机构的可调工作空间展开研究。
(1)利用封闭矢量法求解了含球面副并联机构的运动学方程,综合考虑运动副约束条件,构建了3-PSR并联机构多体动力机械系统及控制系统;
(2)以主要影响因素:滑杆的移动行程和连杆杆长之比为λ,PID多体动力控制系统研究分析得到该机构在不同的影响因素λ时的工作空间图,达到可调工作空间的目的;
(3)结果表明,含球面副并联机构的位置工作空间形状规整、内部连贯,内部无明显连续的空洞;3-PSR并联机构的可调位置工作空间随着λ的增大,该机构的可达工作空间X,Y,Z向的数值也随之变大,从中比对可知,机构的可调位置工作空间范围有限,形状规整分布均匀;在X和Y向的工作空间呈对称形式。
(4)该机构的工作空间体积随着影响因素λ的增大呈现拟线性的变化过程,对机器人后续应用设计提供了重要依据。
