一道物理极值问题引发的思考

张书玮

(内蒙古包头市第一中学 014040)

一、题目与参考答案

题目如图1所示，一根长为l的均匀细杆可以绕通过其一端的水平轴O在竖直平面内转动，杆最初处在水平位置. 杆上距O为a处放有一小物体(可视为质点)，杆与其上小物体最初均处于静止状态，若此杆突然以匀角速度ω绕O轴运动. 问：当ω取什么值时小物体与杆可能相碰?

参考答案:

当ω较小时物体正好撞晨杆的边缘，转过小半圆周，

当ω较大时物体也撞晨边缘，转过大半圆周，

二、参考答案的反思

本题答案直接选用特定位置计算极值：物体与杆在杆端相遇. 本题中，需要满足什么条件才能使杆长对结论没有影响，从而可以选用杆端相碰作为特值来求解答案呢？我们在此作一讨论：

当ω取较小值时，即杆转动小圈时碰撞的情形. 设杆上距O为a处放有一可视为质点的小物体，杆以角速度ω匀速转动，物体与杆在杆的某位置(点C)相碰，所需时间为t，t时刻内物体下落高度为h.

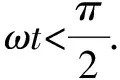
若此函数为单调递增函数，即满足物体下落时间越长，杆与物体碰撞所需角速度越大时，杆长对结果必无影响，则特值法可用，物体与杆在杆端碰撞时可解极值.

于是我们继续进行下一步分析：杆长对结果是否产生影响，如何影响？当函数值ω在(0，ω)这一区间进行取值时，将对应两个自变量t. 即假设碰撞后杆与物体的运动状态皆不改变，当0<ω<ω0时，杆可与物体碰撞两次.

此时我们对第二次碰撞进行分析，杆与物体运动状态均改变，则不可能达到t2时刻进行第二次相碰，即不能在杆端相碰.由此得出，此时杆长l与下落时间t形成了相互制约关系，从而影响对ω极值进行讨论. 杆长对所求量ω产生影响，则不能使用特值，即杆端碰撞取ω极值这一情况进行计算.

对杆长l与时间t的制约关系进行讨论.

设杆长l0，物体下落时间为t0，下落高度h0，杆以角速度ω0转动，杆与物体恰在杆端相碰.①当l>l0时，如图3为几何关系示意图，点M、B、C、D分别为物体初始时刻位置、ta时刻位置、t0时刻位置与tb时刻位置，点A、A1、A2、A3分别为杆端初始时刻位置、ta时刻位置、t0时刻位置与tb时刻位置，点D与A3重合. 设|MB|=ha,|MD|=hb,|MC|=h0.

要使物体与杆在杆端相碰，物体下落时间tb必然大于杆长为l0时杆端相碰(点C)的用时t0，即此时用杆端相碰特值所求ωA实则对应ta、tb两值(图4)，下落高度分别为ha、hb. 即假设碰撞不改变运动状态，物体可与杆两次相遇(点B、点A′)，且杆端相碰情形中，物体下落高度为hb，下落时间tb，是第二次碰撞.

而第一次碰撞后，运动状态必然改变，即物体与杆必在ωA相对应的ta(0l0)，当ω取ω0，物体可与杆在距O点l0处相碰，ω0为ω可取到的最大值，而与杆长无关.

②当ω较小时，杆转过小半圆周与物体发生碰撞.

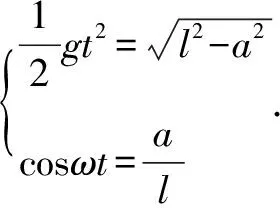
三、讨论过程反思

特值法可以用来排除错误答案，直接用于解题则可能因为其包含情况不完整而导致结论产生偏差. 如本题当中，特值法忽略了杆长对结论的影响，虽思路及运算简便，但思维与逻辑不够严谨. 我们在解决习题时，应养成多角度思考、不放过任何一种可能性，最终排除多余项，从而得出正确结论的良好习惯，这样才能培养思维的全面性与严谨性.

在对本题的讨论中，我与导师进行多次交流，将假设出的情况分别进行讨论验证，对多余限制条件一一排除，最终整合出较完整的结果，受益良多.